সদিক রাশি
বস্তু জগতে যা কিছু পরিমাপ করা যায় তাকেই রাশি বলে। যেমন— দৈর্ঘ্য, ভর, তড়িৎ প্রাবল্য ইত্যাদি সবই রাশি। বস্তু জগতের এই সকল ভৌত রাশিকে বর্ণনার জন্য কোন কোনটির দিক নির্দেশের প্রয়োজন হয়, আর কোনটির ক্ষেত্রে দিক নির্দেশের প্রয়োজন হয় না। তাই দিক নির্দেশনার ভিত্তিতে যাবতীয় রাশিকে সদিক রাশি ও অদিক রাশি এ দুভাগে ভাগ করা যায়। যে সকল পরিমাপযোগ্য ভৌত রাশিকে সম্পূর্ণরূপে প্রকাশ করবার জন্য মান ও দিক উভয়েরই প্রয়োজন হয় তাদেরকে সদিক রাশি বা দিক রাশি বা ভেক্টর রাশি বলা হয়[১]। যেমন— সরণ, ওজন, বেগ, ত্বরণ, বল, তড়িৎ প্রাবল্য ইত্যাদি হল ভেক্টর রাশি। আর যে সকল ভৌত রাশিকে শুধু মান দ্বারা সম্পূর্ণরূপে প্রকাশ করা যায়, দিক নির্দেশের প্রয়োজন হয় না তাদেরকে অদিক রাশি বা দিকশূন্য রাশি বা স্কেলার রাশি বলে। দৈর্ঘ্য, ভর, দ্রুতি, কাজ, তড়িৎ বিভব ইত্যাদি স্কেলার রাশির উদাহরণ। পদার্থবিজ্ঞান ও গাণিতিক ক্ষেত্রে ভেক্টরের ভূমিকা অনন্য।
ইতিহাস
[সম্পাদনা]আজকের দিনে আমরা ভেক্টর বলতে যা বুঝে থাকি তা দুশ বছরেরও বেশি সময় ধরে বিকশিত হয়ে এসেছে। প্রায় ডজন খানেক মানুষ এর পিছনে তাৎপর্যপূর্ণ অবদান রাখেন।[২]
ইটালিয়ান গণিতবিদ জিউস্টো বেলাভিটিস ১৮৩৫ খ্রীস্টাব্দে সমানতার ধারণা প্রতিষ্ঠা করার মাধ্যমে ভেক্টরের মৌলিক ধারণার সূত্রপাত করেন। ইউক্লিডীয় সমতল নিয়ে কাজ করে তিনি একই দৈর্ঘ্য ও দিক বিশিষ্ট যে কোন এক জোড়া রেখাংশের সমানতার প্রণয়ন করেন। কার্যত তিনি সমতলীয় বিন্দু যুগলের (bipoints) সমতুল্যতার অন্বয় নিরূপণ করেন এবং এভাবে তিনি সমতলীয় ভেক্টরের আদি বিষয়-বস্তু খাড়া করেন।[২]:৫২–৪
আইরিশ গণিতবিদ উইলিয়াম রোয়ান হ্যামিল্টন ভেক্টরকে চৌঠায়ন বা চার-সমষ্টির অংশ হিসেবে উপস্থাপন করেন যা একটি বাস্তব সংখ্যা (স্কেলার) q = s + v এবং একটি ত্রিমাত্রিক ভেক্টর এর সমষ্টি। (চৌঠায়ন বা চার-সমষ্টি বা চার বস্তুর সমষ্টি হল এক প্রকার সংখ্যা পদ্ধতি যা জটিল সংখ্যাকে সম্প্রসারিত করে। চার-সমষ্টিকে সাধারণত প্রকাশ করা হয় আকারে যেখানে , , ও হল বাস্তব সংখ্যা এবং i, j ও k হল মৌলিক চার-সমষ্টি একক। ১৮৪৩ সালে হ্যামিল্টন চার-সমষ্টির ধারণা দেন)। বেলাভিটিসের ন্যায় হ্যামিল্টনও ভেক্টরকে সমমুখী রেখাংশ বর্গের প্রতিনিধি হিসেবে পর্যবেক্ষণ করেন। বাস্তব রেখায় জটিল সংখ্যার পরিপূরক কাল্পনিক একক এর মত হ্যামিল্টন v ভেক্টরকে চার-সমষ্টির কাল্পনিক অংশ হিসেবে বিবেচনা করেন।
- একটি সরল রেখা বা ব্যাসার্ধ ভেক্টরের মাধ্যমে জ্যামিতিকভাবে গঠনকৃত বীজগাণিতিক কাল্পনিক অংশটি, প্রতিটি নির্দিষ্ট চার-সমষ্টির জন্য সচরাচর কোন স্থানে যার নির্দিষ্ট দৈর্ঘ্য ও নির্দিষ্ট দিক রয়েছে, তাকে চার-সমষ্টির ভেক্টর অংশ অথবা সাধারণভাবে ভেক্টর বলা যেতে পারে।[৩]
ঊনবিংশ শতকের মধ্যভাগে অগাস্টিন কশি, হের্মান গ্রাসমান, অগাস্ট মোবিয়াস, ডি সেন্ট-ভেন্যান্ট এবং ম্যাথু ওব্রায়েন সহ অন্যান্য কয়েকজন গণিতবিদ ভেক্টর সদৃশ পদ্ধতিগুলোর উন্নতি ঘটান। গ্রাসমানের Theorie der Ebbe und Flut (ভাটা ও প্রবাহের তত্ত্ব, ১৮৪০) এ প্রথম আজকের দিনের মত স্থানিক বিশ্লেষণের দেখা পাওয়া যায়; এতে ভেক্টর গুণন, স্কেলার গুণন এবং ভেক্টর ব্যবকলনের মত ধারণাগুলোও ছিল। গ্রাসমানের কাজ ১৮৭০ সাল পর্যন্ত অবহেলিত ছিল।[২]
হ্যামিল্টনের পর পিটার গুথ্রি টেইট চার-সমষ্টির আদর্শ রূপ প্রদান করেন। পিটার টেইট তার Elementary Treatise of Quaternions(১৮৬৭) বইয়ে নাবলা বা ডেল অপারেটর ∇ এর আচরণ বিস্তারিতভাবে অন্তর্ভুক্ত করেন।
১৮৭৮ খ্রীস্টাব্দে উইলিয়াম কিংডন ক্লিফোর্ডের Elements of Dynamic প্রকাশিত হয়। ক্লিফোর্ড সমগ্র চার-সমষ্টি গুণন থেকে দুটি ভেক্টরের ভেক্টর গুণন ও স্কেলার গুণণকে আলাদা করার মাধ্যমে চার-সমষ্টি সংক্রান্ত গবেষণা-অধ্যয়নকে সহজতর করে তুলেন যা ভেক্টর ক্যালকুলাসকে প্রকৌশলীদের নিকট এবং তিন-মাত্রা ও চতুর্থ সংশয়বাদীতা নিয়ে কাজ করা অন্যান্যদের নিকট সহজলভ্য করে।
জোসিয়াহ উইলার্ড গিবস জেমস ক্লার্ক ম্যাক্সওয়েলের Treatise on Electricity and Magnetism এর মাধ্যমে প্রভাবিত হন। তিনি অন্যান্য অংশ থেকে ভেক্টরকে আলাদা করেন এবং ভেক্টর ক্যালকুলাসের উন্নতি সাধন করেন। ১৮৮১ সালে গিবসের Elements of Vector Analysis এর প্রথম অর্ধাংশ প্রকাশিত হয়, এই অংশে তিনি মূলত ভেক্টর বিশ্লেষণের আধুনিক পদ্ধতির বর্ণনা দেন। ১৯০১ সালে এডউইন বিডওয়েল উইলসন তার Vector Analysis প্রকাশ করেন, যা গিবসের বক্তৃতাগুলোর অভিযোজন। বিডওয়েল তার বইয়ে চার-সমষ্টির ধারণাকে দূর করে দেন।
ভেক্টর রাশির উপস্থাপনা
[সম্পাদনা]
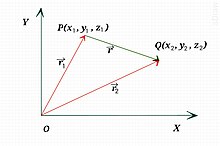
জ্যামিতিক উপায়ে কোন ভেক্টরকে একটি তীর চিহ্নিত সরলরেখা দ্বারা নির্দেশ করা হয়। সরলরেখার দৈর্ঘ্য ভেক্টর রাশিটির মান ও তীর চিহ্ন ভেক্টর রাশিটির দিক নির্দেশ করে। চিত্রে তীর চিহ্নিত সরলরেখাটি = ভেক্টরকে নির্দেশ করছে। রেখাটির দৈর্ঘ্য ও তীর চিহ্ন ভেক্টররাশির যথাক্রমে মান ও দিক। এই ভেক্টরটির দিক বিন্দু থেকে বিন্দুর দিকে। ভেক্টরকে দিয়ে এবং ভেক্টরের মানকে বা দিয়ে নির্দেশ করা হয়। ভেক্টরের বিন্দুকে পাদবিন্দু বাসূচনা বিন্দু বা প্রারম্ভিক বিন্দু বা আদি বিন্দু এবং বিন্দুকে শীর্ষবিন্দু বা প্রান্তিক বিন্দু বলে।
হাতে লিখে ভেক্টর রাশি প্রকাশের সময় সচরাচর নিচের তিনটি পদ্ধতির যেকোন একটি ব্যবহার করা হয়।
- রাশিটির সংকেতের উপর তীর চিহ্ন দিয়ে যেমন: ,
- রাশিটির সংকেতের উপর রেখা চিহ্ন দিয়ে যেমন: এবং
- রাশিটির সংকেতের নিচে রেখা চিহ্ন দিয়ে যেমন: A
ছাপার ক্ষেত্রে সাধারণত মোটা হরফ দিয়ে অর্থাৎ অক্ষরটিকে বোল্ড করে ভেক্টর রাশি বুঝানো হয় (যেমন: A) এবং সরু হরফ দিয়ে বা মডুলাস চিহ্ন দিয়ে ভেক্টর রাশির মান বুঝানো হয় (যেমন: A বা |A|)।
এছাড়াও টিল্ডা (~) দিয়ে ও ভাঙা হরফের মাধ্যমে ভেক্টর রাশি প্রকাশের রীতিও বিদ্যমান (যেমন: , , )।
ভেক্টরের মান
[সম্পাদনা]কোন ভেক্টর রাশির মান বলতে এর পরম মানকে বুঝায় এবং একে A বা |A| বা লিখে ব্যক্ত করা হয়। এখানে "| |" প্রতীকটি module বা পরম মান প্রকাশ করে। পরম মান সর্বদা ধনাত্মক বা শূন্য হয় এবং তা কখনোই ঋণাত্মক হয় না। একারণে ভেক্টর রাশির মান ও স্কেলার রাশি শুধু ধনাত্মক অথবা শূন্য হবে এবং তা কখনোই ঋণাত্মক হবে না। অর্থাৎ ঋণাত্মক বেগ থাকলেও এর মান ধনাত্মক হবে এবং ঋণাত্মক দ্রুতি কখনোই পাওয়া সম্ভব নয়।
মৌলিক ধর্ম
[সম্পাদনা]কার্তেসীয় স্থানাংক ব্যবস্থায় নিম্নরূপ তিনটি একক ভেক্টর (basis vector) বিবেচনা করা যাক, আরও ধরা যাক এই ভেক্টরগুলো একটি সাধারণ বিন্দু থেকে উৎপত্তি হয়েছে।
অতএব আমরা a ভেক্টরকে লিখতে পারি—
নিচের প্রসঙ্গগুলো আমরা এই একক ভেক্টরগুলোর (basis vector) আলোকে আলোচনা করব।
সমতা
[সম্পাদনা]দুটি ভেক্টরের মান ও দিক একই হলে তাদেরকে সমান ভেক্টর বলা হবে। সমতুল্যভাবে বলা যায, তাদের স্থানাঙ্কগুলো সমান হলে এরা পরস্পরের সমান হবে।
- এবং ভেক্টরদ্বয় সমান হবে যদি
- হয়।
বিপরীত, সদৃশ এবং বিসদৃশ ভেক্টর
[সম্পাদনা]দুটি ভেক্টরের মান সমান কিন্তু দিক বিপরীতমুখী হলে এরা পরস্পরের বিপরীত ভেক্টর হবে।
- সুতরাং এবং ভেক্টরদ্বয় বিপরীত হবে যদি
- হয়।
যেকোন মানের দুটি ভেক্টরের দিক একই হলে তাদেরকে সদৃশ বা সমান্তরাল বলা হয়, এক্ষেত্রে ভেক্টরদ্বয়ের মান সমান হওয়া জরুরি নয়। আর যেকোন মানের দুটি ভেক্টরের দিক বিপরীতমুখী হলে তাদেরকে বিসদৃশ বা প্রতি-সমান্তরাল বলা হয়।
যোগ এবং বিয়োগ
[সম্পাদনা]ধরা যাক, a ও b যে কোন মান ও দিক যুক্ত একই জাতীয় দুটি ভেক্টর। a ও b এর যোগফল হবে
একটি ভেক্টরের মাথার (শীর্ষবিন্দু) সাথে দ্বিতীয় ভেক্টরের লেজকে (পাদবিন্দু) যুক্ত করে সবশেষে প্রথমটির লেজের সাথে দ্বিতীয়টির মাথাকে সংযুক্ত করে চিত্রের মাধ্যমে ভেক্টরের যোগকে উপস্থাপন করা যায়। a + b কে নিম্নরূপে চিত্রিত করা যায়:

ভেক্টর যোগের পদ্ধতিটিকে সামান্তরিকের সূত্রও বলা হয়। কারণ a ও b কোন সামান্তরিকের দুটি সন্নিহিত বাহু হলে a + b সামান্তরিকটির একটি কর্ণ নির্দেশ করে। a ও b সন্নিহিত ভেক্টর হলে অর্থাৎ পরস্পরকে ছেদ করলে a + b ভেক্টরও ঐ ছেদবিন্দুগামী হবে। জ্যামিতিকভাবে a + b = b + a এবং (a + b) + c = a + (b + c) প্রমাণ করা যায়।
a ও b ভেক্টরদ্বয়ের পার্থক্য হবে
দুটি ভেক্টরের বিয়োগকে জ্যামিতিকভাবে নিম্নরূপে চিত্রিত করা যায়:
- a থেকে b করতে হলে a ও b উভয়ের লেজকে একই বিন্দুতে যুক্ত করে b এর মাথা থেকে a এর মাথার দিকে সংযুক্ত করে তীর আঁকলে এ তীরই a − b ভেক্টর নির্দেশ করে।

বিভিন্ন প্রকার ভেক্টর
[সম্পাদনা]গাণিতিক ব্যবহার অনুযায়ী ভেক্টরকে নিম্নরূপ ভাবে বিভক্ত করা যায়।
সমান ভেক্টর ===(Equal Vectors)
[সম্পাদনা]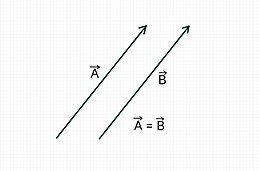
সমজাতীয় দুটি ভেক্টরের মান ও দিক যদি একই হয় তবে তাদেরকে সমান ভেক্টর বলে। জ্যামিতিক আকারে প্রকাশ করল এদের ধারক রেখা একই বা সমান্তরাল হবে। চিত্রে ও ভেক্টরদুটি সমান অর্থাৎ = ।
দুটি ভেক্টরের সমতা এদের পাদবিন্দুর অবস্থানের উপর নির্ভর করে না। পাদবিন্দু যেখানেই থাক না কেন যদি ভেক্টরদ্বয়ের মান সমান এবং দিক একই হয়, তাহলেই তারা সমান হবে। একই দিকে নির্দেশিত সমান দৈর্ঘ্যের দুটি সমান্তরাল রেখা দিয়ে দুটি সমান ভেক্টর বোঝানো হয়।
বিপরীত বা ঋণাত্মক ভেক্টর
[সম্পাদনা]
একই জাতীয় দুটি ভেক্টরের মান সমান হলে কিন্তু দিক বিপরীত হলে তাদেরকে বিপরীত ভেক্টর বলে। এদের একটিকে অপরটির ঋণাত্মক ভেক্টরও বলা যায়। চিত্রে ও একই জাতীয় দুটি ভেক্টর। এদের মান সমান, অর্থাৎ = কিন্তু দিক বিপরীত, সুতরাং = —।
সদৃশ বা সমান্তরাল ভেক্টর
[সম্পাদনা]
সমজাতীয় ও অসম মানের একাধিক ভেক্টর যদি একই দিকে ক্রিয়াশীল থাকে তাহলে তাদেরকে পরস্পরের সদৃশ বা সমান্তরাল ভেক্টর বলে।
বিসদৃশ ভেক্টর
[সম্পাদনা]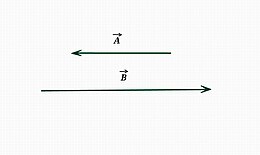
সমজাতীয় ও যে কোন মানের দুইটি ভেক্টর যদি পরস্পরের বিপরীত দিকে ক্রিয়াশীল হয় তাহলে তাদের একটিকে অপরটির বিসদৃশ ভেক্টর বলে। একে unlike বা anti-parallel ভেক্টরও বলা হয়।
সমরেখ ভেক্টর
[সম্পাদনা]
দুই বা ততোধিক ভেক্টর যদি একই তলে একই সরলরেখা বরাবর বা পরস্পর সমান্তরালে ক্রিয়া করে তবে তাদেরকে সমরেখ ভেক্টর বলা হয়। এরা সমজাতীয় বা সমমানের ভেক্টর হতেও পারে আবার নাও হতে পারে। যেমন: একটি গাড়ি সোজা পথে চলার সময় এর বেগ ক্রমাগত বৃদ্ধি পেতে থাকলে এর সরণ ও ত্বরণ সমরেখ হবে, যেহেতু গাড়িটির সরণ ও ত্বরণ একই রেখা বরাবর ঘটছে।
সমতলীয় ভেক্টর
[সম্পাদনা]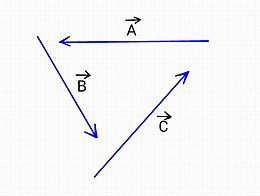
দুই বা ততোধিক ভেক্টর যদি একই তলে অবস্থান করে তবে তাদেরকে সমতলীয় ভেক্টর বলে। এরা সমজাতীয় বা সমমানের বা পরস্পরের সমান্তরাল হতেও পারে আবার নাও হতে পারে। যেমন: কোন টেবিলের মসৃণ উপরিতলে পিঁপড়া ছেড়ে দিলে তাদের সরণ বা বেগ সমতলীয় হবে।
সঠিক ভেক্টর
[সম্পাদনা]যে ভেক্টরের মান শূন্য নয় তাকে সঠিক ভেক্টর বলে।
শূন্য বা নাল ভেক্টর
[সম্পাদনা]যে সব ভেক্টরের মান শূন্য তাদেরকে শূন্য ভেক্টর বা নাল ভেক্টর বলে। একটি ভেক্টরের সাথে তার বিপরীত ভেক্টর যোগ করে বা দুটি সমান ভেক্টর বিয়োগ করে নাল ভেক্টর পাওয়া যায়।
স্বাধীন ভেক্টর
[সম্পাদনা]কোনো ভেক্টরের পাদবিন্দু যদি ইচ্ছামতো নির্ধারণ করা যায়, তাহলে সেই ভেক্টরকে স্বাধীন ভেক্টর বলে।
সীমাবদ্ধ ভেক্টর
[সম্পাদনা]যে ভেক্টরের পাদবিন্দু নির্ধারিত থাকে তাকে সীমাবদ্ধ ভেক্টর বলে।
বিপ্রতীপ বা ব্যতিহার ভেক্টর
[সম্পাদনা]সমজাতীয় দুটি সমান্তরাল ভেক্টরের একটির মান যদি অপরটির বিপরীত সংখ্যা হয় তবে তাদেরকে বিপ্রতীপ বা ব্যতিহার ভেক্টর বলে। যেমন: = ও = হলে ও ভেক্টরদ্বয়কে পরস্পরের বিপ্রতীপ বা ব্যতিহার ভেক্টর বলা হবে।
স্পর্শক ভেক্টর
[সম্পাদনা]একক ভেক্টর
[সম্পাদনা]
যে সব ভেক্টরের মান এক একক তাদেরকে একক ভেক্টর বলা হয়। মান শূন্য নয় এমন কোন ভেক্টরকে তার মান দ্বারা ভাগ করলে উক্ত ভেক্টরের সমান্তরাল একক ভেক্টর পাওয়া যায়। একক ভেক্টরের দিক হবে পূর্বোক্ত ভেক্টরের দিক।
ধরা যাক, একটি ভেক্টর যার সংখ্যাগত মান ≠ , তাহলে = একটি একক ভেক্টর। ভেক্টরের মান একক এবং দিক এর দিকে। ভেক্টরের আলোচনায় একক ভেক্টরের গুরুত্ব অপরিসীম। তাই সচরাচর একক ভেক্টরকে আলাদা সংকেতের মাধ্যমে প্রকাশ করা হয় এবং তা হচ্ছে অক্ষরের উপর তীর চিহ্নের পরিবর্তে টুপি (hat) চিহ্ন (^), যেমন: বা ।
আয়ত একক ভেক্টর
[সম্পাদনা]
ত্রিমাত্রিক কার্তেসীয় স্থানাঙ্ক ব্যবস্থার তিনটি ধনাত্মক অক্ষ বরাবর যে তিনটি একক ভেক্টর বিবেচনা করা হয় তাদেরকে আয়ত একক ভেক্টর বলে।
কোন বিন্দুর অবস্থান নির্দেশ করতে স্থানাঙ্ক ব্যবস্থার প্রয়োজন হয়। সমতলে অবস্থিত কোন বিন্দুর অবস্থান দ্বিমাত্রিক স্থানাঙ্ক ব্যবস্থার সাহায্যে নির্দেশ করা হয়। দুটি অক্ষ ও যদি পরস্পরের সাথে লম্বভাবে অবস্থান করে তবে তাকে দ্বিমাত্রিক কার্তেসীয় স্থানাঙ্ক ব্যবস্থা বা দ্বিমাত্রিক আয়ত স্থানাঙ্ক ব্যবস্থা বলে। কোন স্থানে কোন বিন্দুর অবস্থান নির্দেশ করতে ত্রিমাত্রিক কার্তেসীয় স্থানাঙ্ক ব্যবস্থার প্রয়োজন। তিনটি অক্ষ , ও যদি পরস্পরের সাথে লম্বভাবে অবস্থান করে তবে তাকে ত্রিমাত্রিক কার্তেসীয় স্থানাঙ্ক ব্যবস্থা (Three Dimensional Cartesian Coordinate System) বা ত্রিমাত্রিক আয়ত স্থানাঙ্ক ব্যবস্থা বলা হয়। একটি ডানহাতি স্ক্রুকে অক্ষ থেকে অক্ষের দিকে ক্ষুদ্রতর কোণে ঘুরালে যদি স্ক্রুটি অক্ষ বরাবর অগ্রসর হয় তাহলে সেই স্থানাঙ্ক ব্যবস্থাকে ডানহাতি আয়ত স্থানাঙ্ক ব্যবস্থা (Right Handed Rectangular Co-ordinate System) বলে।
ডানহাতি আয়ত স্থানাঙ্ক ব্যবস্থার তিনটি অক্ষ বরাবর বিবেচিত একক ভেক্টরগুলোকে আয়ত একক ভেক্টর বলে।
প্রকাশ: ত্রিমাত্রিক কার্তেসীয় স্থানাঙ্ক ব্যবস্থার
- ধনাত্মক অক্ষ বরাবর একক ভেক্টরকে ,
- ধনাত্মক অক্ষ বরাবর একক ভেক্টরকে এবং
- ধনাত্মক অক্ষ বরাবর একক ভেক্টরকে ধরা হয়।
যেমন: ধনাত্মক অক্ষ বরাবর 4 এককের একটি ভেক্টর থাকলে সেটি হবে, ঋণাত্মক অক্ষ বরাবর 10 এককের একটি ভেক্টর হবে — এবং হবে ধনাত্মক অক্ষ বরাবর 6 এককের ভেক্টর।
অবস্থান ভেক্টর
[সম্পাদনা]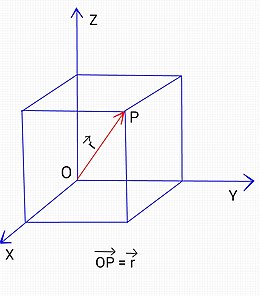
প্রসঙ্গ কাঠামোর মূল বিন্দুর সাপেক্ষে ঐ স্থানের কোন বিন্দুর অবস্থানকে নির্দেশ করার জন্য যে ভেক্টর ব্যবহার করা হয়, তাকে ঐ বিন্দুর অবস্থান ভেক্টর বলে। অবস্থান ভেক্টরকে অনেক সময় ব্যাসার্ধ ভেক্টর বলা হয় এবং দিয়ে প্রকাশ করা হয়। চিত্রে হচ্ছে প্রসঙ্গ কাঠামোর মূল বিন্দু এবং যে কোন একটি বিন্দু। এখানে হল বিন্দুর অবস্থান ভেক্টর এবং =
সরণ ভেক্টর
[সম্পাদনা]কোন বস্তুর অবস্থান ভেক্টর এর পরিবর্তন কে সরণ ভেক্টর বলে।
পোলার ভেক্টর
[সম্পাদনা]কোনো স্থানাঙ্ক তলে অবস্থিত ভেক্টর যা তার পরিমাণ এবং প্রসঙ্গ কাঠামোর অক্ষের সাথে সৃষ্ট কোন দ্বারা নির্ণয় করা হয় তাকে পোলার ভেক্টর বলে।
লদ্ধি ভেক্টর
[সম্পাদনা]দুই বা ততোধিক ফেক্টর যোগ করলে যে নতুন ভেক্টর পাওয়া যায়,তাকে লদ্ধি ভেক্টর বলে।
ভেক্টর অপারেটর
[সম্পাদনা]ভেক্টর অপারেটর হল একটি ডিফারেন্সিয়াল (ব্যাবকলনীয়) অপারেটর যা ভেক্টর ক্যাল্কুলাস এ ব্যবহৃত হয়।ভেক্টর অপারেটর তিন ধরনের হয়;
- গ্র্যাডিয়েন্ট।
- ডাইভারজেন্স।
- কার্ল।
কার্ল
[সম্পাদনা]ত্রিমাত্রিক ভেক্টর ডিফারেন্সিয়াল অপারেটরের সাথে যদি কোনো ত্রিমাত্রিক ভেক্টর ক্ষেত্রে ক্রস গুণফল হয় তখন তাকে কার্ল বলে।
ভেক্টর বীজগণিত
[সম্পাদনা]ভেক্টর রাশির যোগ সাধারণ বীজগণিতের নিয়মে হয় না। এর জন্য ভেক্টর জ্যামিতি ব্যবহার করা হয়। [১]
ভেক্টরের যোগ
[সম্পাদনা]দুটি ভেক্টরের যোগফলকে ভেক্টর দুটোর লব্ধি বলা হয়। ধরা যাক , দুটি ভেক্টর a এবং এর b এর লব্ধি a + b বের করতে হবে। এক্ষেত্রে প্রথমে a ভেক্টরটির শীর্ষবিন্দু, b ভেক্টরের পাদবিন্দুতে স্থাপন করতে হবে। এরপর a এর পাদবিন্দু এবং b এর শীর্ষবিন্দু সংযোগকারী রেখা অঙ্কন করতে হবে। এই সংযোজক সরলরেখাটিই a ও b এর লব্ধি নির্দেশ করবে।

অথবা a এবং b ভেক্টর দুটিকে যদি সামান্তরিকের দুটি সন্নিহিত বাহুর মাধ্যমে নির্দেশ করা যায়, তবে সামান্তরিকের কর্ণটিই ভেক্টর a ও b এর লব্ধি নির্দেশ করবে।
ভেক্টরের বিয়োগ
[সম্পাদনা]ধরা যাক দুটি ভেক্টর a এবং এর b এর বিয়োগফল বের করতে হবে। এক্ষেত্রে পূর্বের মত প্রথমে a ভেক্টরটির শীর্ষবিন্দু , b ভেক্টরের পাদবিন্দুতে স্থাপন করতে হবে। কিন্তু এবার a এর শীর্ষবিন্দু এবং b এর পাদবিন্দু সংযোগকারী রেখা অঙ্কন করতে হবে।এই সংযোজক সরল লেখাটি দ্বারা a ও b এর বিয়োগফল নির্ণয় করা যাবে।
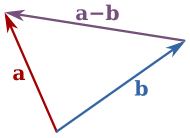
এছাড়া a ভেক্টরের সাথে ঋণাত্মক b ভেক্টর যোগ করলে a ও b এর বিয়োগফল পাওয়া যাবে।
ডট গুণ/স্কেলার গুণ
[সম্পাদনা]দুটি ভেক্টর রাশির গুণফল যদি একটি স্কেলার হয় তবে তাকে ডট গুণ অথবা স্কেলার গুণ বলা হয়ে থাকে। এবং এই গুণফলের মান রাশিদ্বয়ের মান এবং এদের অন্তর্গত কোণের কোসাইনের (cosine) গুণফলের সমান। গাণিতিকভাবে এটিকে নিম্নরূপে উপস্থাপন করা যায়-
এখানে a এবং b হলো দুটি ভেক্টর আর θ হলো a এবং b এর মধ্যকার কোণ।
ক্রস গুণন/ভেক্টর গুণন
[সম্পাদনা]দুটি ভেক্টর রাশির গুণফল যদি একটি ভেক্টর হয় তবে তাকে ক্রস গুণন অথবা ভেক্টর গুণন বলা হয়ে থাকে।এবং এই গুণফলের মান রাশিদ্বয়ের মান এসং এদের অন্তর্গত কোণের sine-এর গুণফলের সমান। এবং এই গুণফল এর দিক ডানহাতি স্ক্রু-র নিয়ম অনুসরন করে। গাণিতিক ভাবে এটিকে নিম্নরূপে উপস্থাপন করা যায়-
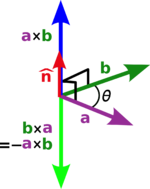
এখানে θ হলো a এবং b এর মধ্যকার কোণ, এর n হলো একক ভেক্টর যেটি a এবং b এর লম্ব বরাবর অবস্থিত। ডান পাশের চিত্রটি লক্ষ্য করলে বিষয়টি আরও পরিষ্কার হবে।
ভেক্টর ক্যালকুলাস
[সম্পাদনা]ভেক্টরকে অনেক সময় ব্যবকলনের মাধ্যমেও (Directional derivative) প্রকাশ করা হয়। ধরা যাক সমীকরনটি একটি ফাংশন এবং সমীকরনটি একটি বক্ররেখা (Curve) উপস্তাপন করে। তাহলে কে সংজ্ঞায়িত করা যায় এভাবে-
যেখানে হচ্ছে নির্দিষ্ট মাত্রার (dimensions এর) Summation convention (যেমন: ত্রিমাত্রিক ইউক্লিডিয় কাঠামোতে এর মাত্রা ১ থেকে ৩ পর্যন্ত , আবার চতুর্মাত্রিক কাঠামোতে এর মাত্রা হবে ০ থেকে৩ পর্যন্ত)। এখন ধরা যাক যেকোন একটি ভেক্টর বক্র রেখাটির সাথে স্পর্শক রূপে বিদ্যমান। তাহলে ভেক্টর নির্দেশকারী সমীকরনটি হবেঃ
এছাড়া ফাংশন বাদ দিয়ে আমরা ভেক্টকে ভেক্টর ব্যবকলন এর মাধ্যমেও (derivative) উপস্থাপন করতে পারি -
সুতরাং বলা যায় কোন নির্দিষ্ট ভেক্টরকে একটি নির্দিষ্ট directional derivative এর মাধ্যমেও প্রাশ করা যায় । তাই ভেক্টরকে এককথায় এভাবে উপস্থাপন করা যায়-
আরও দেখুন
[সম্পাদনা]তথ্যসূত্র
[সম্পাদনা]- ↑ ক খ "২.৩ স্কেলার রাশি ও ভেক্টর রাশি" (bangla ভাষায়)। ২০২০-০৮-২০ তারিখে মূল থেকে আর্কাইভ করা। সংগ্রহের তারিখ ২০১৬-১২-০১।
- ↑ ক খ গ Michael J. Crowe, A History of Vector Analysis; see also his "lecture notes" (পিডিএফ)। জানুয়ারি ২৬, ২০০৪ তারিখে মূল (পিডিএফ) থেকে আর্কাইভ করা। সংগ্রহের তারিখ ২০১০-০৯-০৪। on the subject.
- ↑ W. R. Hamilton (1846) London, Edinburgh & Dublin Philosophical Magazine 3rd series 29 27



























































