ভরবেগ

ভরবেগ।
ভরবেগ।
	সংঘর্ষের পর পুল খেলায় কিউ বলের ভরবেগ, জড়োকৃত বলগুলোয় স্থানান্তরিত হয়।
সাধারণ প্রতীক	p, p
এসআই একক	কিলোগ্রাম⋅মিটার/সেকেন্ড; kg⋅m/s
অন্যান্য একক	স্লাগ⋅ফুট/সেকেন্ড; slug⋅ft/s
সংরক্ষিত?	হ্যাঁ
মাত্রা	[MLT−1]

চিরায়ত বলবিদ্যায় ভরবেগ হলো কোনো গতিশীল বস্তুর ভর ও বেগের গুণফল। একে রৈখিক ভরবেগও বলা হয়ে থাকে। বেগের ন্যায় রৈখিক ভরবেগ বা ভরবেগও একটি ভেক্টর রাশি, অর্থাৎ এর মান এবং দিক উভয়ই আছে। এস্‌ আই পদ্ধতিতে ভরবেগের একক হলো কিলোগ্রাম-মিটার/সেকেন্ড (kg m/s), বা নিউটন-সেকেন্ড (N s)। বস্তুর ভর m এবং বেগ v হলে, ভরবেগের সাধারণ সমীকরণ:

$\mathbf {p} =m\mathbf {v} .$

নিউটনের গতির দ্বিতীয় সূত্র অনুযায়ী কোনো বস্তুর ভরবেগ পরিবর্তনের হার, এর উপর প্রযুক্ত কার্যকর বলের সমানুপাতিক। ভরবেগ প্রসঙ্গ কাঠামোর উপর নির্ভরশীল, তবে জড় প্রসঙ্গ কাঠামোতে এটি একটি সংরক্ষিত রাশি অর্থাৎ কোনো বদ্ধ সিস্টেম বাহ্যিক বল দ্বারা প্রভাবিত না হলে এর মোট রৈখিক ভরবেগ অপরিবর্তিত থাকে। পরিবর্তিত আকারে তড়িচ্চুম্বকত্ব, কোয়ান্টাম বলবিজ্ঞান, কোয়ান্টাম ক্ষেত্র তত্ত্ব ও সাধারণ আপেক্ষিকতা এবং বিশেষ আপেক্ষিকতার ক্ষেত্রেও (রূপান্তরিত একটি সূত্রের সাহায্যে) ভরবেগ সংরক্ষিত থাকে। এটি স্থান এবং কালের অন্যতম মৌলিক প্রতিসাম্যতা, ট্রান্সলেশনাল প্রতিসাম্যের অভিব্যক্তি।

চিরায়ত বলবিদ্যার উন্নত রূপ, ল্যাগ্রাঞ্জীয় এবং হ্যামিল্টনীয় বলবিদ্যার মাধ্যমে প্রতিসাম্যতা বিশিষ্ট স্থানাঙ্ক ব্যবস্থা ব্যবহারের সুযোগ তৈরী হয়। এই সিস্টেমগুলোতে সংরক্ষিত পরিমাণ হলো জেনারালাইজড বা সাধারণীকৃত ভরবেগ, যা পূর্বে উল্লেখিত গতীয় ভরবেগ থেকে ভিন্ন। সাধারণীকৃত ভরবেগের ধারণা কোয়ান্টাম বলবিজ্ঞানেও ব্যবহৃত হয়, যেখানে এটি তরঙ্গ ফাংশনের একটি অপারেটরে পরিণত হয়। ভরবেগ এবং অবস্থান অপারেটর হাইজেনবার্গের অনিশ্চয়তা নীতির সাথে সম্পর্কিত।

তড়িচ্চুম্বকীয় ক্ষেত্র, প্রবাহী গতিবিজ্ঞান এবং নমনীয় বস্তুর মত পরিবর্তনশীল সিস্টেমের ক্ষেত্রে ভরবেগ ঘনত্ব সংজ্ঞায়িত করা যায়। ভরবেগ সংরক্ষণের সাংতত্যক সংস্করণের ফলে তরলের ক্ষেত্রে নেভিয়ার-স্টোকস্‌ সমীকরণ অথবা নমনীয় বস্তু বা তরলের ক্ষেত্রে কোশি ভরবেগ সমীকরণের মত সমীকরণ তৈরী হয়েছে।

নিউটনীয় বলবিজ্ঞান

ভরবেগের যেমন একটি দিক রয়েছে তেমনি মানও রয়েছে। যেসকল ভৌত রাশির মান ও দিক উভয়ই বিদ্যমান তাদেরকে ভেক্টর রাশি বলা হয়। যেহেতু ভরবেগের দিক বিদ্যমান, তাই এটি ব্যবহার করে সংঘর্ষের পরে বস্তুগুলো কোন দিক অভিমুখে গতিশীল হবে এবং তাদের গতি কি হবে তা নির্ণয় করা যায় । একক মাত্রায় ভরবেগের সাধারণ ধর্মাবলী নিম্নে বর্ণনা করা হল। এখানে ভেক্টর সমীকরণগুলো স্কেলার সমীকরণগুলোর প্রায় অনুরূপ।

একক বস্তুকণার ক্ষেত্রে

কোন বস্তুকণার ভরবেগকে ইংরেজি বর্ণ $p$ দ্বারা প্রকাশ করা হয়ে থাকে। এটি হল, ভর ( $m$ দ্বারা প্রকাশিত ) ও বেগ ( $v$ দ্বারা প্রকাশিত), এই দুটি ভৌত রাশির গুণফল।^[১]

p=mv.

ভরবেগের একক হল ভর ও বেগের এককের গুণফল। এস আই এককে যদি ভরের একক কিলোগ্রাম ও বেগের একক মিটার/সেকেন্ড হয় তাহলে ভরবেগের একক হবে কিলোগ্রাম মিটার/সেকেন্ড (সংক্ষেপে বাংলায় কেজি. মি./সে. ও ইংরেজিতে $kgms^{-}1$ )।

একটি ভেক্টর রাশি হওয়ার দরূন ভরবেগের মান ও দিক উভয়ই বিদ্যমান। উদাহরণস্বরূপ, যদি ১ কেজি ভরের কোন নমুনা উড়োজাহাজ সোজা উত্তর দিক বরাবর সরলরেখায় ১ মি./সে. বেগে সুষম উচ্চতায় উড়তে থাকে, তাহলে ভূমির সাপেক্ষে পরিমাপ করলে তার ভরবেগ হবে উত্তর দিক বরাবর ১ কেজি. মি./সে.।

একাধিক বস্তুকণার ক্ষেত্রে

কোন ভৌত ব্যবস্থার ভরবেগ ঐ ব্যবস্থা সৃষ্টিকারী কণাসমূহের ভরবেগের সমষ্টির সমান। যদি যেকোন দুটি গতিশীল কণার ভর যথাক্রমে $m 1$ ও $m 2$ হয় এবং এদের বেগ যথাক্রমে $v 1$ ও $v 2$ হয়, তাহলে বস্তুকণাদ্বয়ের ভরবেগের সমষ্টি

{\begin{aligned}p&=p_{1}+p_{2}\\&=m_{1}v_{1}+m_{2}v_{2}\,.\end{aligned}}

একাধিক কণার ভরবেগ নির্ণয়ের আরো সাধারণ সূত্র হলো:

$p=\sum _{i}m_{i}v_{i}$

বহু কণার সমন্বয়ে গঠিত কোন ব্যবস্থার একটি অভিন্ন ভরকেন্দ্র থাকে। এই কেন্দ্রটি মূলত এমন একটি বিন্দু যেখানে ব্যবস্থা সৃষ্টিকারী সকল কণার ভর কেন্দ্রীভূত হয়:

r_{\text{cm}}={\frac {m_{1}r_{1}+m_{2}r_{2}+\cdots }{m_{1}+m_{2}+\cdots }}={\frac {\sum \limits _{i}m_{i}r_{i}}{\sum \limits _{i}m_{i}}}

যদি সকল কণাই সরলরেখায় গতিশীল হয়, তাহলে ভরকেন্দ্রটিও সমান তালে গতিশীল হবে । তবে ঘূর্ণন গতির ক্ষেত্রে ভরকেন্দ্রের অবস্থান অপরিবর্তিত থাকে (যখন ব্যবস্থাটি নিজ অক্ষের চারিদিকে আবর্তিত হয়, যেমন- লাটিম)। এক্ষেত্রে যদি ভরকেন্দ্রটি $v cm$ বেগে গতিশীল হয়, তাহলে এর ভরবেগ হবে:

p=mv_{\text{cm}}.

এটি অয়লারের ১ম সূত্র হিসেবে পরিচিত.^[২]^[৩]

বলের সাথে সম্পর্ক

যদি কোন বল $F$ কোনো কণার উপর নির্দিষ্ট সময় $Δ t$ ব্যাপী ক্রিয়া করে, তাহলে ঐ বস্তুকণার ভরবেগের পরিবর্তন হবে নিম্নরূপ:

\Delta p=F\Delta t\,.

একে অন্তরীকরণ হিসেবে প্রকাশ করলে নিউটনের গতির ২য় সূত্রে উপনীত হওয়া যায়। অর্থাৎ, বস্তুর ভরবেগের পরিবর্তনের হার এর উপর প্রযুক্ত বলের সমানুপাতিক। প্রযুক্ত বল $F$ এর জন্য সমীকরণ দাড়ায়^[১]:

F={\frac {dp}{dt}}.

যদি বল সময়ের একটি ফাংশন F(t) হয় তাহলে $t 1$ থেকে $t 2$ সময়ের মধ্যে ভরবেগের পরিবর্তন (বা, ঘাত J ):

\Delta p=J=\int _{t_{1}}^{t_{2}}F(t)\,dt\,

ঘাত নিউটন সেকেন্ড (1 N⋅s = 1 kg⋅m/s) অথবা ডাইন সেকেন্ড (1 dyne⋅s = 1 g⋅cm/s) এককে পরিমাপ করা হয়।

নিউটনের ২য় সূত্রটি কেবলমাত্র এমন বস্তুকণার ক্ষেত্রেই প্রযোজ্য যা এর আশেপাশের পরিবেশের সাথে কোন ভর বিনিময় করে না^[৪]। অতএব লেখা যেতে পারে:

F={\frac {d(mv)}{dt}}=m{\frac {dv}{dt}}=ma,

তাই নেট বল হলো বস্তুর ত্বরণ ও তার ভরের গুণফলের সমান।

উদাহরণস্বরূপ, যদি ১ কেজি ভরের কোনো নমুনা উড়োজাহাজ স্থির অবস্থা থেকে ২ সেকেন্ডে সোজা উত্তর দিক বরাবর ৬ মি./সে. বেগে পৌঁছায়, তবে এই ত্বরণ অর্জনে প্রয়জনীয় নেট বল হলো উত্তর দিক বরাবর ৩ নিউটন। ভরবেগের পরিবর্তন হলো উত্তর দিক বরাবর ৩ কেজি মি./সে, যা সংখ্যাগতভাবে ৩টি নিউটনের সমতুল্য।

সংরক্ষণশীলতা

বদ্ধ সিস্টেমে (যা পরিবেশের সাথে পদার্থ বিনিময় করেনা এবং বাহ্যিক বলের ক্রিয়ার আওতাধীন নয়) মোট ভরবেগের পরিমাণ ধ্রুব। ভরবেগের সংরক্ষণশীলতার সূত্র নামে পরিচিত এই তথ্য নিউটনের গতিসূত্রসমূহ থেকে পাওয়া যায়।^[৫]^[৬] উদাহরণস্বরূপ, ধরা যাক, দুটি কণার মধ্যে সংঘর্ষ হয়। তৃতীয় সূত্র অনুযায়ী, তাদের মধ্যকার বল সমান এবং বিপরীত। কণাদ্বয়কে 1 এবং 2 চিহ্নিত করা হলে, নিউটনের দ্বিতীয় সূত্র অনুযায়ী, $F1 = .mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:100%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:2px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0em 0em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}+dp১/dt$ এবং $F 2 = + dp ২ / dt$ । ফলে,

{\frac {dp_{1}}{dt}}=-{\frac {dp_{2}}{dt}},

এখানে ঋণাত্মক চিহ্ন নির্দেশ করে যে বলদ্বয় বিপরীতমুখী। একইভাবে,

{\frac {d}{dt}}\left(p_{1}+p_{2}\right)=0

যদি সংঘর্ষের পুর্বে কণাদ্বয়ের বেগ $u 1$ এবং $u 2$ হয়, এবং পরে $v 1$ and $v 2$ হয় তবে,

m_{1}u_{1}+m_{2}u_{2}=m_{1}v_{1}+m_{2}v_{2}

কণাসমূহের মধ্যে বল যত জটিলই হোক না কেন, এই সূত্র প্রযোজ্য হবে। একইভাবে, যদি বহু কণা থাকে তবে প্রত্যেক জোড়া কণার মধ্যবর্তী ভরবেগের বিনিময়ের সমষ্টি শূন্য হয়, যার ফলে ভরবেগের মোট পরিবর্তন শূন্য হয়। এই সংরক্ষণ সূত্র বিস্ফোরণ সহ সকল সংঘর্ষের ক্ষেত্রে প্রযোজ্য।^[৫] এছাড়াও এর সর্বজনীন রূপ, যেখানে নিউটনের আইন প্রযোজ্য নয় সেখানেও ব্যবহার করা যেতে পারে, যেমন আপেক্ষিকতা তত্ত্ব এবং তড়িচ্চুম্বকত্ব।^[৭]

প্রসঙ্গ কাঠামোর উপর নির্ভরশীলতা

ভরবেগ একটি পরিমাপযোগ্য পরিমাণ, এবং এর পরিমাপ পর্যবেক্ষকের গতির উপর নির্ভর করে। যদি একটি আপেল অবতরণকারী একটি লিফটে অবস্থাণ করে, একজন বাহ্যিক পর্যবেক্ষক, লিফটের দিকে তাকিয়ে দেখবেন আপেল নড়াচড়া করছে, তাই, সেই পর্যবেক্ষকের কাছে আপেলের ভরবেগ অ-শূন্য। কিন্তু লিফটের ভেতরে অবস্থানকারী পর্যবেক্ষকের সাপেক্ষে আপেল নড়াচড়া করে না, অর্থাৎ এর ভরবেগ শূন্য। উভয় পর্যবেক্ষকের আলাদা প্রসঙ্গ কাঠামো রয়েছে, যার সাপেক্ষে তারা গতি পর্যবেক্ষণ করে এবং যদি লিফট ধীরে ধীরে অবতরণ করে, তবে তারা সেই একই নিয়মের সাথে সামঞ্জস্যপূর্ণ ঘটনা দেখতে পাবে।

ধরা যাক, একটি স্থির প্রসঙ্গ কাঠামোতে একটি কণার অবস্থান x। u বেগে গতিশীল আরেকটি প্রসঙ্গ কাঠামো (প্রাইম দ্বারা চিহ্নিত) সময়ের সাথে এইরূপে পরিবর্তিত হয়,

x'=x-ut\,

একে বলে হয় গ্যালিলিয় রূপান্তর। প্রথম প্রসঙ্গ কাঠামোতে যদি কণাটি $+ dx / dt = v$ বেগে গতিশীল হয়, তবে দ্বিতীয়টিতে এর বেগ,

v'={\frac {dx'}{dt}}=v-u\,

$u$ পরিবর্তিত না হওয়ায়, ত্বরণ একই থাকে:

a'={\frac {dv'}{dt}}=a\,

এভাবে, উভয় প্রসঙ্গ কাঠামোতেই ভরবেগ সংরক্ষিত থাকে। উপরন্তু, উভয় প্রসঙ্গ কাঠামোতে শক্তি একই রূপে থাকলে নিউটনের দ্বিতীয় সূত্র অপরিবর্তিত থাকে। নিউটনীয় মাধ্যাকর্ষণের মত শুধুমাত্র বস্তুর স্কেলার দূরত্বের উপর নির্ভরশীল বলের ক্ষেত্রে, এই শর্ত পূরণ হয়। প্রসঙ্গ কাঠামোর এই স্বাধীনতাকে বলা হয় নিউটনীয় আপেক্ষিকতা বা গ্যালিলিয় আপেক্ষিকতা।

প্রসঙ্গ কাঠামোর সামান্য পরিবর্তন, গতির গণনা সরল করে ফেলতে পারে। উদাহরণস্বরূপ, দুটি কণার সংঘর্ষের ক্ষেত্রে, একটি প্রসঙ্গ কাঠামো বাছাই করা যেতে পারে, যেখানে কণা স্থির অবস্থান থেকে গতিশীল হয়। আরেকটি বহুল ব্যবহৃত প্রসঙ্গ কাঠামো হলো ভরকেন্দ্র কাঠামো – যা ভরকেন্দ্রের সাথে একইসাথে গতিশীল। এই কাঠামোতে, মোট ভরবেগ শূন্য।

সংঘর্ষের ক্ষেত্রে প্রয়োগ

শুধুমাত্র ভরবেগের সংরক্ষণ সূত্র ব্যবহার করে সংঘর্ষের পর কণার গতিবেগ নির্ণয় করা সম্ভব হয়না। গতির আরেকটি বৈশিষ্ট্য, গতিশক্তিও জানা থাকতে হয়। এটি সর্বদা সংরক্ষিত থাকে না। যদি গতিশক্তি সংরক্ষিত থাকে তবে তাকে স্থিতিস্থাপক সংঘর্ষ এবং না থাকলে অস্থিতিস্থাপক সংঘর্ষ বলা হয়।

স্থিতিস্থাপক সংঘর্ষ

যে সংঘর্ষে গতিশক্তি সংরক্ষিত থাকে তাই স্থিতিস্থাপক সংঘর্ষ। সংঘর্ষ পুরোপুরি স্থিতিস্থাপক হয় যখন বস্তু একে অপরকে স্পর্শ করে না, যেমন পারমাণবিক বা নিউক্লীয় বিচ্ছুরণের ক্ষেত্রে বৈদ্যুতিক বিকর্ষণ কণাগুলোকে পৃথক রাখে। গ্রহের মহাকর্ষ ব্যবহার করে কৃত্রিম উপগ্রহের গতিপথ পরিবর্তনের ঘটনাটিকেও স্থিতিস্থাপক সংঘর্ষ বলা যায়। অনমনীয়তার কারণে, দুইটি পুল বলের মধ্যে সংঘর্ষকে প্রায় সম্পূর্ণ স্থিতিস্থাপক সংঘর্ষ বলা যায়, কিন্তু যখন বস্তু একে অপরের সংস্পর্শে আসে তখন সবসময়ই শক্তির কিছুটা ক্ষয় হয়।^[৮]

সমান ভরের বস্তুর ক্ষেত্রে স্থিতিস্থাপক সংঘর্ষ।

অসমান ভরের বস্তুর ক্ষেত্রে স্থিতিস্থাপক সংঘর্ষ।

দুইটি বস্তুর মধ্যে মুখোমুখি সংঘর্ষ, বস্তুদ্বয়ের মধ্য দিয়ে অঙ্কিত রেখা একটি রেখা বরাবর একমাত্রিক গতির মাধ্যমে প্রকাশ করা যেতে পারে। যদি সংঘর্ষের পূর্বে বেগদ্বয় u₁ ও u₂ এবং সংঘর্ষের পর বেগদ্বয় v₁ ও v₂ হয় তবে ভরবেগ ও গতিশক্তির সংরক্ষণশীলতা প্রদর্শনকারী সমীকরণ:

{\begin{aligned}m_{1}u_{1}+m_{2}u_{2}&=m_{1}v_{1}+m_{2}v_{2}\\{\tfrac {1}{2}}m_{1}u_{1}^{2}+{\tfrac {1}{2}}m_{2}u_{2}^{2}&={\tfrac {1}{2}}m_{1}v_{1}^{2}+{\tfrac {1}{2}}m_{2}v_{2}^{2}\,\end{aligned}}

প্রসঙ্গ কাঠামোর পরিবর্তন এই হিসাবকে আরো সহজ করে দিতে পারে। উদাহরণস্বরূপ, সমান ভর m বিশিষ্ট দুটি বস্তুর একটি স্থির এবং অপরটি v বেগে প্রথমটির দিকে গতিশীল (চিত্রের অনুরূপ)। ভরকেন্দ্র v/2 বেগে গতিশীল এবং উভয় বস্তু এর দিকে v/2 বেগে গতিশীল। সূত্র অনুযায়ী, সংঘর্ষের পর উভয়েই ভরকেন্দ্র থেকে সমান বেগে সরে যাবে। উভয় বস্তুর বেগের সাথে ভরকেন্দ্রের বেগ যোগ করে আমরা পাই যে গতিশীল বস্তুটি এখন স্থির এবং অপরটি v বেগে সরে যাচ্ছে। বস্তু দুইটি তাদের বেগ বিনিময় করেছে। এদের বেগ যাই হোক না কেন, ভরকেন্দ্র কাঠামোর পরিবর্তনে এক্ষেত্রে একই সিদ্ধান্তে পৌঁছানো যাবে। ফলে, তাদের শেষবেগ হবে^[৫]

{\begin{aligned}v_{1}&=u_{2}\\v_{2}&=u_{1}\,.\end{aligned}}

সাধারণভাবে, আদিবেগ দেওয়া থাকলে শেষবেগ নির্ণয়ের উপায়:^[৯]

v_{1}=\left({\frac {m_{1}-m_{2}}{m_{1}+m_{2}}}\right)u_{1}+\left({\frac {2m_{2}}{m_{1}+m_{2}}}\right)u_{2}\,

v_{2}=\left({\frac {m_{2}-m_{1}}{m_{1}+m_{2}}}\right)u_{2}+\left({\frac {2m_{1}}{m_{1}+m_{2}}}\right)u_{1}\,.

যদি একটি বস্তুর ভর অপরটি থেকে অনেক বেশি হয়, তবে বেশি ভরের বস্তুর সংঘর্ষের দ্বারা সামান্যই প্রভাবিত হবে কিন্তু অপর বস্তুটির ক্ষেত্রে বড় পরিবর্তন সাধিত হবে।

অস্থিতিস্থাপক সংঘর্ষ

অস্থিতিস্থাপক সংঘর্ষের ক্ষেত্রে, বস্তুসমূহের কিছু গতিশক্তি অন্য কোনো শক্তিতে রূপান্তরিত হয় (যেমন তাপ বা শব্দ)। যানবাহনের সংঘর্ষের ক্ষেত্রে গতিশক্তির পরিবর্তন যানবাহনের ক্ষতির মাধ্যমে লক্ষ্য করা যায়; ইলেকট্রন, পরমাণুর কাছে তাদের কিছু শক্তি হারায় (ফ্রাঙ্ক-হার্জ পরীক্ষার অনুরূপ); এবং কণার ত্বরণে গতিশক্তি নতুন কণার আকারে ভরে রূপান্তরিত হয়।

সমান ভরের বস্তুর ক্ষেত্রে পূর্ণ অস্থিতিস্থাপক সংঘর্ষ।

পূর্ণ অস্থিতিস্থাপক সংঘর্ষের ক্ষেত্রে, সংঘর্ষের পর উভয় বস্তু একই গতি লাভ করে। দুইটি বস্তুর মধ্যে মুখোমুখি সংঘর্ষ, বস্তুদ্বয়ের মধ্য দিয়ে অঙ্কিত একটি রেখা বরাবর একমাত্রিক গতির মাধ্যমে প্রকাশ করা যেতে পারে। যদি সংঘর্ষের পূর্বে বেগদ্বয় u₁ ও u₂ হয় তবে সংঘর্ষের পর তাদের বেগ হবে v। ভরবেগের সংরক্ষণ প্রকাশকারী সমীকরণ:

{\begin{aligned}m_{1}u_{1}+m_{2}u_{2}&=\left(m_{1}+m_{2}\right)v\,.\end{aligned}}

যদি শুরুতে একটি বস্তুর বেগ শূন্য হয় (যেমন $u_{2}=0$ ) তবে ভরবেগের সংরক্ষণশীলতার সমীকরণ:

m_{1}u_{1}=\left(m_{1}+m_{2}\right)v\,,

তাহলে

v={\frac {m_{1}}{m_{1}+m_{2}}}u_{1}\,.

অন্য ঘটনায়, যদি প্রসঙ্গ কাঠামো শেষবেগ $v=0$ নিয়ে গতিশীল হয়, তবে একটি অস্থিতিস্থাপক সংঘর্ষের মাধ্যমে বস্তুসমূহকে স্থির করা যাবে এবং গতিশক্তির ১০০% অন্য শক্তিতে রূপান্তরিত হবে। এই ক্ষেত্রে, বস্তুসমূহের আদিবেগ অ-শূন্য হতে হয়, নাহলে তাদেরকে ভরবিহীন হতে হবে।

অস্থিতিস্থাপক সংঘর্ষের একটি পরিমাপ হলো রেস্টিটিউশন গুণাঙ্ক, $C R$ , যা সংঘর্ষের আদি আপেক্ষিক বেগ ও শেষ আপেক্ষিক বেগ হিসেবে প্রকাশিত। একটি কঠিন পৃষ্ঠ থেকে একটি বল বাউন্সের ক্ষেত্রে এটি নিম্নলিখিত সূত্র ব্যবহার করে সহজেই পরিমাপ করা যেতে পারে:

C_{\text{R}}={\sqrt {\frac {\text{bounce height}}{\text{drop height}}}}\,.

বস্তুসমূহ একত্রে গতিশীল হয়ে পরে আলাদা হয়ে গেলে সেখানেও ভরবেগ এবং শক্তির সমীকরণ প্রযোজ্য হবে। উদাহরণস্বরূপ, বিস্ফোরণ একটি চেইন বিক্রিয়ার ফলাফল, যা রাসায়নিক, যান্ত্রিক বা পারমাণবিক আকারে সঞ্চিত বিভব শক্তিকে গতিশক্তি, শব্দশক্তি, এবং তড়িৎ-চৌম্বকীয় বিকিরণে রূপান্তরিত করে। রকেটের ক্ষেত্রেও ভরবেগের সংরক্ষণশীলতা প্রযোজ্য: প্রোপেল্যান্ট নিচের দিকে বল প্রয়োগ করে ভরবেগ লাভ করে এবং একটি সমান ও বিপরীত ভরবেগ রকেটের ওপর ক্রিয়া করে।

বহুমাত্রিক

বাস্তব গতির দিক এবং বেগ উভয়ই আছে, তাই একে ভেক্টর দ্বারা প্রকাশ করতে হয়। $x, y, z$ অক্ষ বিশিষ্ট স্থানাঙ্ক ব্যবস্থায় $x$ -অক্ষ বরাবর বেগের উপাংশ $v x$ , $y$ -অক্ষ বরাবর $v y$ এবং $z$ -অক্ষ বরাবর $v z$ । ভেক্টর গাঢ় অক্ষর দ্বারা চিহ্নিত:^[৫]

\mathbf {v} =\left(v_{x},v_{y},v_{z}\right).

একইভাবে, ভরবেগ একটি ভেক্টর পরিমাপ এবং গাঢ় অক্ষর দ্বারা প্রকাশিত:

\mathbf {p} =\left(p_{x},p_{y},p_{z}\right).

পূর্ববর্তী অনুচ্ছেদগুলোর সমীকরণসমূহ, ভেক্টর রূপে কাজ করবে যদি স্কেলার $p$ ও $v$ , ভেক্টর $p$ ও $v$ দ্বারা প্রতিস্থাপিত হয়। প্রতিটি ভেক্টর সমীকরণ তিনটি স্কেলার সমীকরণ উপস্থাপণ করে। উদাহরণস্বরূপ,

\mathbf {p} =m\mathbf {v}

তিনটি সমীকরণ উপস্থাপন করে:^[৫]

{\begin{aligned}p_{x}&=mv_{x}\\p_{y}&=mv_{y}\\p_{z}&=mv_{z}.\end{aligned}}

গতিশক্তির সমীকরণগুলো অবশ্য উপর্যুক্ত প্রতিস্থাপন সূত্রের ব্যতিক্রম। সমীকরণগুলো এখনও একমাত্রিক, কিন্তু প্রতিটি স্কেলার পরিমাপ, ভেক্টরের মান উপস্থাপণ করে। উদাহরণস্বরূপ,

v^{2}=v_{x}^{2}+v_{y}^{2}+v_{z}^{2}\,.

প্রতিটি ভেক্টর সমীকরণ তিনটি স্কেলার সমীকরণের প্রতিনিধিত্ব করে। স্থানাঙ্ক এমনভাবেও নির্বাচন করা যেতে পারে যাতে চিত্রের মত শুধুমাত্র দুটি উপাংশ প্রয়োজন হয়। প্রতিটি উপাংশ পৃথকভাবে পাওয়া যায় এবং ফলাফল একত্রিত করে একটি ভেক্টর ফলাফল উৎপাদন করা যায়।^[৫]

একটি সাধারণ ভরকেন্দ্র কাঠামো কেন্দ্র ব্যবহার করে দেখানো যেতে পারে যে, যদি একটি স্থির স্থিতিস্থাপক গোলককে একটি চলন্ত গোলক দ্বারা আঘাত করা হয়, সংঘর্ষের পর গোলক দুটি সমকোণে চলে যাবে (চিত্রের ন্যায়)।^[১০]

পরিবর্তনশীল ভরের বস্তু

পরিবর্তনশীল ভরের বস্তু যেমন জ্বালানী নির্গতকারী রকেট বা গ্যাস বিবৃদ্ধিকারী তারা ইত্যাদির আচরণ ব্যাখ্যায় ভরবেগের ধারণা মৌলিক ভূমিকা পালন করে। এধরনের বস্তু বিশ্লেষণের সময় বস্তুটির ভরকে সময়ের ফাংশন: $m (t)$ ধরে নেওয়া হয়। ফলে $t$ সময়ে বস্তুর ভরবেগ $p (t) = m (t) v (t)$ । বস্তুর ওপর বাহ্যিক বল $F$ এর ভরবেগ $p (t)$ এর সাথে $F = + dp / dt$ দ্বারা সম্পর্কিত দেখিয়ে এখানে নিউটনের গতির দ্বিতীয় সূত্র সংযুক্ত করার চেষ্টা করা হতে পারে। কিন্তু এটি সঠিক নয়, যা $+ d (mv) / dt$ এর ওপর গুণন বিধি প্রয়োগ করে প্রাপ্ত রাশির ক্ষেত্রেও প্রযোজ্য:^[১১]

F=m(t){\frac {dv}{dt}}+v(t){\frac {dm}{dt}}.

(ত্রুটিপূর্ণ)

এই সমীকরণ পরিবর্তনশীল ভরের বস্তুর গতি সঠিকভাবে বর্ণনা করে না। সঠিক সমীকরণ হলো:

F=m(t){\frac {dv}{dt}}-u{\frac {dm}{dt}},

যেখানে $u$ হলো বস্তুর স্থির কাঠামোয় পর্যবেক্ষিত নির্গত ভর।^[১১] এটা $v$ থেকে আলাদা, যা জড় কাঠামোয় বস্তুর নিজস্ব বেগ নির্দেশ করে।

এই সমীকরণটি বস্তুর ভরবেগ এবং একই সাথে বহিষ্কৃত/অর্জিত ভরের ভরবেগ (dm) উভয় হিসাব করে নির্ণীত। একসাথে বিবেচনা করা হলে, বস্তু এবং ভর (dm) একটি বদ্ধ সিস্টেম নির্মাণ করে যেখানে মোট ভরবেগ সংরক্ষিত:

P(t+dt)=(m-dm)(v+dv)+dm(v-u)=mv+mdv-udm=P(t)+mdv-udm

আপেক্ষিকতায়

লরেঞ্জ রূপান্তরে

চিরায়ত বলবিদ্যায় পর্যবেক্ষকের বাইরে পরম সময় এবং স্থান বিদ্যমান বলে ধরে নেওয়া হয়, যা গ্যালিলিয় আপেক্ষিকতার জন্ম দেয়। এছাড়াও এটি ধারণা দেয় যে আলোর গতি এক প্রসঙ্গ কাঠামো থেকে অন্য প্রসঙ্গ কাঠামোতে ভিন্ন হতে পারে। এই তথ্য পর্যবেক্ষণের পরিপন্থী। বিশেষ আপেক্ষিকতা তত্ত্বে আইনস্টাইন, গতির সমীকরণ প্রসঙ্গ কাঠামোর উপর নির্ভর করে না, এই স্বীকার্য অব্যাহত রাখেন কিন্তু আলোর গতি $c$ আপেক্ষিক ধরে নেন। ফলস্বরূপ, দুটি প্রসঙ্গ কাঠামোতে অবস্থান এবং সময় গ্যালিলিয় রূপান্তরের পরিবর্তে লরেঞ্জ রূপান্তর দ্বারা সম্পর্কিত।^[১২]

উদাহরণস্বরূপ, ধরা যাক, একটি প্রসঙ্গ কাঠামো অন্যটির সাপেক্ষে $v$ বেগে $x$ দিকে গতিশীল। গ্যালিলিয় রূপান্তর অনুযায়ী গতিশীল কাঠামোর স্থানাঙ্ক:

{\begin{aligned}t'&=t\\x'&=x-vt\end{aligned}}

অন্যদিকে, লরেঞ্জ রূপান্তর অনুযায়ী:^[১৩]

{\begin{aligned}t'&=\gamma \left(t-{\frac {vx}{c^{2}}}\right)\\x'&=\gamma \left(x-vt\right)\,\end{aligned}}

যেখানে $γ$ হলো লরেঞ্জ ফ্যাক্টর।

ভর স্থির থাকলে, নিউটনের দ্বিতীয় সূত্র লরেঞ্জ রূপান্তরে অপরিবর্তনশীল নয়। তবে, পদার্থের জড় ভর $m$ কে বেগের ফাংশনে রূপান্তরিত করে একে অপরিবর্তনশীল করা যেতে পারে:

m=\gamma m_{0}\,;

$m 0$ হলো বস্তুর স্থির ভর।^[১৪]

পরিবর্তিত ভরবেগ,

\mathbf {p} =\gamma m_{0}\mathbf {v} \,,

নিউটনের দ্বিতীয় সূত্র মেনে চলে:

\mathbf {F} ={\frac {d\mathbf {p} }{dt}}\,.

চিরায়ত বলবিদ্যার অধীনে, আপেক্ষিক ভরবেগ চিরায়ত ভরবেগের খুব কাছাকাছি: নিম্ন বেগে, $γm 0 v$ প্রায় ভরবেগের চিরায়ত প্রকাশ $m 0 v$ এর সমান।

চার-ভেক্টর সূত্র

বিশেষ আপেক্ষিকতা তত্ত্বে, ভৌত পরিমাপসমূহ চার-ভেক্টর হিসেবে প্রকাশিত, যেখানে সাধারণ তিনটি স্থানাঙ্কের সাথে সময়কে চতুর্থ স্থানাঙ্ক হিসেবে অন্তর্ভুক্ত করা হয়েছে। এই ভেক্টরগুলো সাধারণত বড় হাতের অক্ষর দ্বারা প্রকাশিত, যেমন অবস্থানের ক্ষেত্রে $R$ । এক্ষেত্রে ভরবেগের প্রকাশ নির্ভর করে স্থানাঙ্ক কীভাবে প্রকাশিত হয়েছে তার ওপর। সময় তার প্রচলিত একক অথবা আলোর গতি দ্বারা গুণ করে প্রকাশ করা হতে পারে যাতে চার-ভেক্টরের সমস্ত উপাদান দৈর্ঘ্যের মাত্রা বিশিষ্ট হয়। যদি আলোর গতি দ্বারা গুণ করা হয় তবে প্রকৃত সময়, $τ$ , এর সংজ্ঞায়ন:^[১৫]

c^{2}d\tau ^{2}=c^{2}dt^{2}-dx^{2}-dy^{2}-dz^{2}\,,

যা লরেঞ্জ রূপান্তরের অধীনে অপরিবর্তনশীল (এই অভিব্যক্তিতে এবং পরবর্তীতে (+ − − −) মেট্রিক পদ্ধতি ব্যবহার করা হয়েছে, বিভিন্ন লেখক বিভিন্ন প্রথা ব্যবহার করেন)। গাণিতিকভাবে এই অপরিবর্তনশীলতা দুটি উপায়ে নিশ্চিত করা যেতে পারে: ভেক্টর চারটিকে ইউক্লিডীয় ভেক্টর বিবেচনা করা এবং তাদেরকে $\sqrt -১$ দ্বারা গুণ করা ; অথবা সময়কে অক্ষত রাখা এবং মিংকফ্‌স্কি স্থানে ভেক্টরগুলো প্রয়োগ করা।^[১৬] মিংকফ্‌স্কি স্থানে, দুইটি চার-ভেক্টর $U = (U 0, U 1, U 2, U 3)$ এবং $V = (V 0, V 1, V 2, V 3)$ এর স্কেলার গুণফল নিম্নোক্তভাবে সংজ্ঞায়িত:

\mathbf {U} \cdot \mathbf {V} =U_{0}V_{0}-U_{1}V_{1}-U_{2}V_{2}-U_{3}V_{3}\,.

সকল স্থানাঙ্ক ব্যবস্থায়, (কন্ট্রাভেরিয়েন্টভাবে) আপেক্ষিক চার-ভেক্টরের সংজ্ঞায়ন:

\mathbf {U} \equiv {\frac {d\mathbf {R} }{d\tau }}=\gamma {\frac {d\mathbf {R} }{dt}}\,,

এবং এ ব্যবস্থায় ভরবেগ,

\mathbf {P} =m_{0}\mathbf {U} \,,

যেখানে $m 0$ হলো স্থির বভর। যদি $R = (ct,x,y,z)$ (মিংকফ্‌স্কি স্থানে), তবে

\mathbf {P} =\gamma m_{0}\left(c,\mathbf {v} \right)=(mc,\mathbf {p} )\,.

আইনস্টাইনের ভর-শক্তি সমতা, $E = mc 2$ , ব্যবহার করে, এটিকে পরিবর্তন করে লেখা যায়:

\mathbf {P} =\left({\frac {E}{c}},\mathbf {p} \right)\,.

এভাবে, চার-ভেক্টর সূত্রে ভরবেগ ভর এবং শক্তি উভয়েরই সংরক্ষণ নির্দেশ করে।

এই ভরবেগের মান $m 0 c$ এর সমান:

||\mathbf {P} ||^{2}=\mathbf {P} \cdot \mathbf {P} =\gamma ^{2}m_{0}^{2}(c^{2}-v^{2})=(m_{0}c)^{2}\,,

এবং সকল প্রসঙ্গ কাঠামোতেই স্থির।

আপেক্ষিকতার শক্তি–ভরবেগ সম্পর্ক ভরহীন কণা যেমন ফোটনের জন্যও সত্য; $m 0 = 0$ হলে দাঁড়ায়:

E=pc\,.

আপেক্ষিকতার নিয়ম অনুসরণকারী একটি বিলিয়ার্ড খেলায়, যদি একটি স্থির কণা স্থিতিস্থাপক সংঘর্ষে একটি চলন্ত কণার দ্বারা আঘাতপ্রাপ্ত হয়, সংঘর্ষের পর কণা দুটি দ্বারা গঠিত পথ একটি সূক্ষ্মকোণ গঠন করবে। কিন্তু অ-আপেক্ষিক ঘটনার ক্ষেত্রে তারা সমকোণ গঠন করবে।^[১৭]

একটি প্লেনার তরঙ্গের চার-ভরবেগ, একটি তরঙ্গ চার-ভেক্টরের সাথে সম্পর্কিত করা যেতে পারে^[১৮]

\mathbf {P} =\left({\frac {E}{c}},{\vec {\mathbf {p} }}\right)=\hbar \mathbf {K} =\hbar \left({\frac {\omega }{c}},{\vec {\mathbf {k} }}\right)

একটি কণার জন্য, অস্থায়ী অংশকের মধ্যে সম্পর্ক, $E = ħ ω$ , হলো প্ল্যাঙ্ক-আইনস্টাইন সম্পর্ক এবং স্থানিক অংশকের মধ্যে সম্পর্ক, $p = ħ k$ , একটি ডি ব্রগলি পদার্থ তরঙ্গ বর্ণনা করে।

সাধারণীকৃত

নিউটনের সূত্রসমূহ কিছু গতিতে প্রয়োগ করা কঠিন হতে পারে কারণ গতি কিছু সীমাবদ্ধতা দ্বারা সীমাবদ্ধ। উদাহরণস্বরূপ, অ্যাবাকাসের গুটি এর তার বরাবর নড়াচড়া করতে বাধ্য এবং পেন্ডুলামের বব ঝুলন বিন্দু থেকে একটি নির্দিষ্ট দূরত্ব পর্যন্ত দোল খেতে পারে। এইসব সীমাবদ্ধতা, কার্তেসীয় স্থানাঙ্ককে সাধারণীকৃত স্থানাঙ্কের একটি সেট দ্বারা পরিবর্তন করে অন্তর্ভুক্ত করা যেতে পারে।^[১৯] সাধারণীকৃত স্থানাঙ্কে বলবিদ্যার সমস্যা সমাধানের জন্য পরিশোধিত গাণিতিক পদ্ধতি প্রণীত হয়েছে। এর ফলে সাধারণীকৃত ভরবেগ বা অনুবন্ধী ভরবেগের উদ্ভব ঘটে, যা রৈখিক এবং কৌণিক উভয় ভরবেগের ধারণা প্রসারিত করে। ভর এবং বেগের গুণফল থেকে প্রাপ্ত ভরবেগকে সাধারণীকৃত ভরবেগ থেকে আলাদা করার জন্য, পূর্বেরটিকে যান্ত্রিক, গতীয় বা কিনেম্যাটিক ভরবেগ হিসাবে উল্লেখ করা হয়।^[২০]^[২১]^[২২] দুটি প্রধান পদ্ধতি নিচে বর্ণনা করা হল।

ল্যাগ্রাঞ্জীয় বলবিদ্যা

ল্যাগ্রাঞ্জীয় বলবিদ্যায়, ল্যাগরেঞ্জিয় কে গতিশক্তি $T$ এবং বিভবশক্তি $V$ এর মধ্যে পার্থক্য হিসেবে সংজ্ঞায়িত করা হয়:

{\mathcal {L}}=T-V\,.

যদি সাধারণীকৃত স্থানাঙ্ক ভেক্টর $q = (q 1, q 2, ... , q N)$ হিসেবে উপস্থাপিত হয় এবং সময় ব্যবকলন চলকের ওপর একটি বিন্দু হিসেবে প্রকাশিত হয়, তবে গতির সমীকরণসমূহ $N$ সমীকরণের একটি সেট:^[২৩]

{\frac {d}{dt}}\left({\frac {\partial {\mathcal {L}}}{\partial {\dot {q}}_{j}}}\right)-{\frac {\partial {\mathcal {L}}}{\partial q_{j}}}=0\,.

যদি একটি স্থানাঙ্ক $q i$ , কার্তেসীয় স্থানাঙ্ক না হয়, তবে সংশ্লিষ্ট সাধারণীকৃত ভরবেগ অংশক $p i$ অপরিহার্যভাবে রৈখিক ভরবেগের মাত্রা ধারণ করেনা। যদি $q i$ কার্তেসীয় স্থানাঙ্ক হয় তবুও $p i$ যান্ত্রিক ভরবেগের ভরবেগের সমান হবেনা যদি বিভব বেগের ওপর নির্ভরশীল হয়।^[৭] কিছু সূত্র $Π$ প্রতীক দ্বারা গতীয় ভরবেগ প্রকাশ করে।^[২৪]

এই গাণিতিক কাঠামোতে, একটি সাধারণীকৃত ভরবেগ, সাধারণীকৃত স্থানাঙ্কের সাথে সংযুক্ত। এর অংশক নিম্নোক্তভাবে সংজ্ঞায়িত:

p_{j}={\frac {\partial {\mathcal {L}}}{\partial {\dot {q}}_{j}}}\,.

প্রতি অংশক $p j$ , স্থানাঙ্ক $q j$ এর অনুবন্ধী ভরবেগ বলে ধরা হয়।

এখন যদি একটি প্রদত্ত স্থানাঙ্ক $q i$ , ল্যাগরেঞ্জিয়তে প্রদর্শিত না হয় (যদিও এর সময় ব্যবকলন প্রদর্শিত হতে পারে), তবে

p_{j}={\text{constant}}\,.

এটাই ভরবেগের সংরক্ষণশীলতার সাধারণীকরণ।^[৭]

এমনকি যদি সাধারণীকৃত স্থানাঙ্ক শুধুমাত্র সাধারণ স্থানিক স্থানাঙ্ক হয়, তবুও অনুবন্ধী ভরবেগ সাধারণ ভরবেগ স্থানাঙ্ক নাও হতে পারে। তড়িৎচুম্বকত্ব বিভাগে এর একটি উদাহরণ পাওয়া যায়।

হ্যামিল্টনীয় বলবিদ্যা

হ্যামিল্টনীয় বলবিদ্যায়, ল্যাগরেঞ্জিয় (সাধারণীকৃত স্থানাঙ্ক এবং তাদের ব্যবকলনের একটি ফাংশন) কে হ্যামিল্টনিয়, যা সাধারণীকৃত স্থানাঙ্ক ও ভরবেগের ফাংশন, তার দ্বারা প্রতিস্থাপণ করা হয়। হ্যামিল্টনিয় কে নিম্নোক্তভাবে সংজ্ঞায়িত করা হয়:

{\mathcal {H}}\left(\mathbf {q} ,\mathbf {p} ,t\right)=\mathbf {p} \cdot {\dot {\mathbf {q} }}-{\mathcal {L}}\left(\mathbf {q} ,{\dot {\mathbf {q} }},t\right)\,,

যেখানে ভরবেগ, উপরের মত ল্যাগরেঞ্জিয় এর ব্যবকলনের মাধ্যমে প্রাপ্ত। গতির হ্যামিল্টনিয় সমীকরণসমূহ হলো:^[২৫]

{\begin{aligned}{\dot {q}}_{i}&={\frac {\partial {\mathcal {H}}}{\partial p_{i}}}\\-{\dot {p}}_{i}&={\frac {\partial {\mathcal {H}}}{\partial q_{i}}}\\-{\frac {\partial {\mathcal {L}}}{\partial t}}&={\frac {d{\mathcal {H}}}{dt}}\,.\end{aligned}}

ল্যাগ্রাঞ্জীয় বলবিদ্যার মত, হ্যামিল্টনিয় তে সাধারণীকৃত স্থানাঙ্ক প্রদর্শিত না হলে, এর অনুবন্ধী ভরবেগ অংশক সংরক্ষিত থাকে।^[২৬]

প্রতিসাম্য ও সংরক্ষণ

ভরবেগের সংরক্ষণশীলতা স্থানের সমসত্ত্বতার (স্থানান্তর প্রতিসাম্য) একটি গাণিতিক ফলাফল। অর্থাৎ, পদার্থবিজ্ঞানের নীতিসমূহ অবস্থানের উপর নির্ভরশীল না হওয়ার একটি ফলাফল হলো ভরবেগের সংরক্ষণশীলতা; এটি নোয়েদারের উপপাদ্যের একটি বিশেষ ঘটনা।^[২৭] যে সব সিস্টেমের এই প্রতিসাম্যতা নেই, তাদের জন্য ভরবেগের সংরক্ষণশীলতা সংজ্ঞায়িত করা সম্ভব নাও হতে পারে, যেমন সাধারণ আপেক্ষিকতার বক্র স্থানকাল,^[২৮] সময় স্ফটিক বা ঘনপদার্থবিজ্ঞান।^[২৯]^[৩০]^[৩১]^[৩২]

তড়িৎ-চুম্বকীয়

ক্ষেত্রের মধ্যে কণা

ম্যাক্সওয়েলের সমীকরণসমূহে, কণাসমূহের মধ্যবর্তী শক্তি বৈদ্যুতিক এবং চৌম্বক ক্ষেত্র দ্বারা প্রভাবিত হয়। তড়িৎ ক্ষেত্র $E$ এবং চৌম্বক ক্ষেত্র $B$ এর সমন্বয়ের কারণে $q$ চার্জ যুক্ত কণার উপর তড়িচ্চুম্বকীয় বল (লরেঞ্জ বল) হয়

\mathbf {F} =q(\mathbf {E} +\mathbf {v} \times \mathbf {B} ).

(এসআই এককে)।^[৩৩]^:২ এর তড়িৎ বিভব $φ (r, t)$ এবং চৌম্বকীয় ভেক্টর বিভব $A (r, t)$ ।^[২৪] অ-আপেক্ষিক ঘটনায়, এর সাধারণীকৃত ভরবেগ হলো

\mathbf {P} =m\mathbf {\mathbf {v} } +q\mathbf {A} ,

কিন্তু আপেক্ষিক বলবিদ্যায় সূত্রটি

$\mathbf {P} =\gamma m\mathbf {\mathbf {v} } +q\mathbf {A} .$

$V=q\mathbf {A}$ কে অনেকসময় বিভবীয় বা পোটেনশিয়াল ভরবেগ বলা হয়।^[৩৪]^[৩৫]^[৩৬] এটি তড়িচ্চুম্বকীয় ক্ষেত্রের সাথে কণার মিথস্ক্রিয়ার কারণে উদ্ভূত ভরবেগ। নামটি বিভব শক্তি $U=q\varphi$ , যা তড়িচ্চুম্বকীয় ক্ষেত্রের সাথে কণার মিথস্ক্রিয়ার কারণে উদ্ভূত শক্তি, তার সাথে মিল সম্পন্ন। এই পরিমাণ একটি চার-ভেক্টর গঠন করে, তাই সাদৃশ্যটি সঙ্গতিপূর্ণ; এছাড়াও, তড়িচ্চুম্বকীয় ক্ষেত্রের তথাকথিত লুকায়িত ভরবেগ ব্যাখ্যার জন্য পোটেনশিয়াল ভরবেগের ধারণা গুরুত্বপূর্ণ।^[৩৭]

সংরক্ষণশীলতা

চিরায়ত বলবিদ্যায়, ক্রিয়া এবং প্রতিক্রিয়ার নীতি অর্থাৎ প্রতিটি বলের সমান এবং বিপরীত প্রতিক্রিয়া বল আছে, এই নীতি থেকে ভরবেগের সংরক্ষণশীলতার সূত্র পাওয়া যেতে পারে। কিছু পরিস্থিতিতে, গতিশীল চার্জিত কণা অ-বিপরীত দিকে একে অপরের উপর বল প্রয়োগ করতে পারে।^[৩৮] তা সত্ত্বেও, কণা এবং তড়িচ্চুম্বকীয় ক্ষেত্রের সম্মিলিত ভরবেগ সংরক্ষিত হয়।

শূন্যস্থান

লরেঞ্জ বল কণায় একটি ভরবেগ তৈরী করে, তাই নিউটনের দ্বিতীয় সূত্র অনুযায়ী কণারও তড়িচ্চুম্বকীয় ক্ষেত্রে একটি ভরবেগ তৈরী করার কথা।^[৩৯]

শূন্যস্থানে, প্রতি একক আয়তনে ভরবেগ

\mathbf {g} ={\frac {1}{\mu _{0}c^{2}}}\mathbf {E} \times \mathbf {B} \,,

যেখানে $μ 0$ হলো শূন্যস্থান ভেদ্যতা এবং c হলো আলোর বেগ। ভরবেগ ঘনত্ব পয়েন্টিং ভেক্টর S এর সমানুপাতিক, যা প্রতি একক ক্ষেত্রফলে শক্তি স্থানান্তরের হার প্রদান করে^[৩৯]^[৪০]

\mathbf {g} ={\frac {\mathbf {S} }{c^{2}}}\,.

যদি Q অঞ্চল জুড়ে V আয়তনে ভরবেগ সঙ্গরক্ষিত রাখতে হয়, তবে লরেঞ্জ শক্তির মাধ্যমে পদার্থের ভরবেগের পরিবর্তন, তড়িচ্চুম্বকীয় ক্ষেত্রের ভরবেগ এবং ভরবেগ প্রবাহের পরিবর্তনের মাধ্যমে ভারসাম্য বজায় রাখতে হবে। যদি P_mech Q অঞ্চলের সকল কণার ভরবেহ হয় এবং কণাসমূহ সাংতত্যক হিসেবে বিবেচিত হয়, তবে নিউটনের দ্বিতীয় সূত্র প্রদান করে

{\frac {d\mathbf {P} _{\text{mech}}}{dt}}=\iiint \limits _{Q}\left(\rho \mathbf {E} +\mathbf {J} \times \mathbf {B} \right)dV\,.

তড়িচ্চুম্বকীয় ভরবেগ হয়

\mathbf {P} _{\text{field}}={\frac {1}{\mu _{0}c^{2}}}\iiint \limits _{Q}\mathbf {E} \times \mathbf {B} \,dV\,,

ভরবেগের প্রতি অংশক $i$ সংরক্ষণের ক্ষেত্রে সমীকরণ

{\frac {d}{dt}}\left(\mathbf {P} _{\text{mech}}+\mathbf {P} _{\text{field}}\right)_{i}=\iint \limits _{\sigma }\left(\sum \limits _{j}T_{ij}n_{j}\right)d\Sigma \,.

ডানদিকের রাশিটি σ তলের পৃষ্ঠ Σ এর ওপর সমাকলন, যা আয়তনের ভেতরে ও বাইরে ভরবেগের প্রবাহ উপস্থাপন করে এবং n_j, তল S এর একটি অংশক। T_ij রাশিটিকে ম্যাক্সওয়েল স্ট্রেস টেনসর বলা হয়, যার সংজ্ঞায়ন:

T_{ij}\equiv \epsilon _{0}\left(E_{i}E_{j}-{\frac {1}{2}}\delta _{ij}E^{2}\right)+{\frac {1}{\mu _{0}}}\left(B_{i}B_{j}-{\frac {1}{2}}\delta _{ij}B^{2}\right)\,.

মাধ্যম

উপর্যুক্ত ফলাফল আণুবীক্ষণিক ম্যাক্সওয়েল সমীকরণের জন্য ও শূন্যস্থানে তড়িচ্চুম্বকীয় বলের জন্য প্রযোজ্য (অথবা খুব ছোট পরিমাণে মাধ্যমে)। মাধ্যমে ভরবেগ ঘনত্ব নির্ধারণ করা আরো কঠিন কারণ অবাধে এর তড়িচ্চুম্বকীয় এবং যান্ত্রিক বিভাজন ঘটে। তড়িচ্চুম্বকীয় ভরবেগ ঘনত্বের সংজ্ঞা পরিবর্তন করে লেখা হয়

\mathbf {g} ={\frac {1}{c^{2}}}\mathbf {E} \times \mathbf {H} ={\frac {\mathbf {S} }{c^{2}}}\,,

যেখানে H-ক্ষেত্র $H$ , B-ক্ষেত্র এবং চুম্বকায়ন $M$ এর সাথে সম্পর্কিত:

\mathbf {B} =\mu _{0}\left(\mathbf {H} +\mathbf {M} \right)\,.

তড়িচ্চুম্বকীয় স্ট্রেস টেনসর, মাধ্যমের বৈশিষ্ট্যের উপর নির্ভর করে।^[৩৯]

কোয়ান্টাম বলবিজ্ঞানে

কোয়ান্টাম বলবিজ্ঞানে, ভরবেগকে তরঙ্গ ফাংশনে একটি সেলফ-অ্যাডজয়েন্ট অপারেটর হিসেবে সংজ্ঞায়িত করা হয়। হাইজেনবার্গের অনিশ্চয়তা নীতি একটি একক পর্যবেক্ষণযোগ্য সিস্টেমের ভরবেগ এবং অবস্থান কতটা সঠিকভাবে জানা যায় তার সীমা নির্ধারণ করে। কোয়ান্টাম বলবিজ্ঞানে, ভরবেগ এবং অবস্থান অনুবন্ধী চলক।

অবস্থানের ভিত্তিতে বর্ণিত একটি কণার জন্য মোমেন্টাম অপারেটর কে লেখা যেতে পারে

\mathbf {p} ={\hbar  \over i}\nabla =-i\hbar \nabla \,,

যেখানে $\nabla$ হলো গ্র্যাডিয়েন্ট অপারেটর, $ħ$ হলো হ্রাসকৃত প্ল্যাঙ্কের ধ্রুবক এবং $i$ হলো কাল্পনিক একক। এটি ভরবেগ অপারেটরের একটি সাধারণ রূপ, যদিও অন্যান্য ক্ষেত্রে এটি অন্য রূপ নিতে পারে। ভরবেগ স্পেসে, ভরবেগ অপারেটরের উপস্থাপন নিম্নরূপ

\mathbf {p} \psi (p)=p\psi (p)\,,

যেখানে তরঙ্গ ফাংশন $ψ (p)$ এর ওপর কার্যরত অপারেটর $p$ , ঐ ফাংশনকে $p$ এর মান দ্বারা গুণ করে ধারণ করে, যেরকমভাবে তরঙ্গ ফাংশন $ψ (x)$ এর ওপর কার্যরত অবস্থান অপারেটর ঐ ফাংশনকে x মান দ্বারা গুণ করে ধারণ করে।

বৃহৎ এবং ভরহীন উভয় বস্তুর ক্ষেত্রেই, আপেক্ষিক ভরবেগ দশা ধ্রুবক, $\beta$ এর সাথে সম্পর্কিত:^[৪১]

p=\hbar \beta

ফোটন কণা তড়িৎ-চৌম্বকীয় বিকিরণ (দৃশ্যমান আলো, অতিবেগুনী ও বেতার তরঙ্গ সহ) ঘটায়। যদিও ফোটনের (আলোর কণাধর্ম) কোনো ভর নেই, তবুও তাদের ভরবেগ আছে। এর ফলে সৌর পাল বা সোলার সেইল এর মত যন্ত্র তৈরী করা সম্ভব হয়েছে। অস্তরক মাধ্যমে আলোর ভরবেগ গণনা কিছুটা বিতর্কিত (আব্রাহাম-মিংকফ্‌স্কি বিতর্ক দেখুন)।^[৪২]^[৪৩]

স্থিতিস্থাপক বস্তু ও তরলে

সাংতত্যক কাঠামোয় সংরক্ষণ

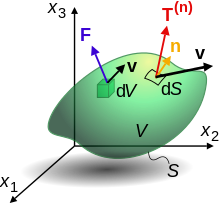
প্রবাহী গতিবিজ্ঞান ও কঠিন বলবিদ্যায়, প্রতিটি পরমাণু বা অণুর ভরবেগ অনুসরণ করা সম্ভব নয়। এর পরিবর্তে, উপাদানগুলোকে একটি কন্টিনাম ধরে নিতে হবে, যেখানে প্রতিটি বিন্দুতে একটি কণা বা তরল পার্সেল থাকে যা কাছাকাছি একটি ছোট অঞ্চলের পরমাণুর গড় বৈশিষ্ট্য ধারণ করবে। নির্দিষ্টভাবে, এর সময় $t$ এবং অবস্থান $r$ এর ওপর নির্ভরশীল ঘনত্ব $ρ$ এবং বেগ $v$ থাকে। প্রতি একক আয়তনে ভরবেগ হলো $ρ v$ ।^[৪৪]

হাইড্রোস্ট্যাটিক বা উদস্থিতিয় সাম্যাবস্থায় একটি পানির স্তম্ভের কথা ধরা যাক। পানির সকল বল ভারসাম্যে থাকে, ফলে পানি নিশ্চল। পানির যে কোন ফোঁটায়, দুটি বল ভারসাম্য বজায় রাখে। প্রথমটি হচ্ছে মাধ্যাকর্ষণ, যা ভেতরের প্রতিটি পরমাণু এবং অণুর উপর সরাসরি কাজ করে। প্রতি একক আয়তনে অভিকর্ষ বল হলো $ρ g$ , যেখানে $g$ হলো অভিকর্ষজ ত্বরণ। দ্বিতীয়টি হচ্ছে পারিপার্শ্বিক পানি দ্বারা এর পৃষ্ঠে প্রয়োগকৃত সকল বলের যোগফল। মাধ্যাকর্ষণ ভারসাম্যের জন্য যতটুকু প্রয়োজন, নিচের দিকের বলটি উপরের দিকের বল থেকে ঠিক ততটাই বড়। প্রতি একক ক্ষেত্রফলে সাধারণ বল হলো চাপ $p$ । একটি ফোঁটার ভেতরে প্রতি একক আয়তনে গড় বল হলো চাপের গ্র্যাডিয়েন্ট, ফলে বল ভারসাম্য সমীকরণ হলো^[৫]

-\nabla p+\rho \mathbf {g} =0\,.

যদি বলের ভারসাম্য না থাকে, তবে ফোঁটাটি ত্বরান্বিত হয়। এই ত্বরণ শুধুমাত্র আংশিক ব্যবকলন $+ \partial v / \partialt$ নয় কারণ সময়ের সাথে ঐ নির্দিষ্ট আয়তনে তরলের পরিবর্তন ঘটে। এর পরিবর্তে, উপাদান ব্যবকলন (ম্যাটেরিয়াল ডেরিভেটিভ) প্রয়োজন:^[৪৪]

{\frac {D}{Dt}}\equiv {\frac {\partial }{\partial t}}+\mathbf {v} \cdot {\boldsymbol {\nabla }}\,.

যে কোন ভৌত পরিমাণে প্রয়োগ উপযোগী, উপাদান ব্যবকলন, একটি বিন্দুতে পরিবর্তনের হার এবং বিন্দুতে তরলের প্রবাহের ফলে সকল পরিবর্তন অন্তর্ভুক্ত করে। প্রতি একক আয়তনে, ভরবেগ পরিবর্তনের হার হলো $ρ + D v / Dt$ । এটা ফোঁটার ওপর ক্রিয়ারত নেট বলের সমান।

যে সব বল একটি ফোঁটার ভরবেগ পরিবর্তন করতে পারে, তা হলো উপরের ন্যায় চাপ এবং মাধ্যাকর্ষণ গ্র্যাডিয়েন্ট। এছাড়া, পৃষ্ঠের বলসমূহও ফোঁটায় পরিবর্তন সাধন করতে পারে। সবচেয়ে সহজ ঘটনা, ড্রপলেট পৃষ্ঠের সমান্তরাল একটি শক্তি দ্বারা প্রয়োগকৃত শিয়ার স্ট্রেস বা পীড়ন, $τ$ , বিকৃতির হারের সমানুপাতিক। তরলের বেগ গ্র্যাডিয়েন্ট থাকলে অর্থাৎ তরল এক দিকে অন্য দিকের চেয়ে দ্রুত গতিতে চলতে থাকলে এধরনের পীড়নের উদ্ভব ঘটে। যদি $x$ অক্ষের গতি, $z$ অক্ষের সাথে পরিবর্তিত হয়, তবে $z$ অক্ষের সাপেক্ষে $x$ অক্ষের প্রতি একক ক্ষেত্রফলে ট্যানজেন্ট বল:

\sigma _{\text{zx}}=-\mu {\frac {\partial v_{x}}{\partial z}}\,,

যেখানে $μ$ হলো সান্দ্রতা। এছাড়াও এটি একটি ফ্লাক্স, অথবা পৃষ্ঠের প্রতি একক ক্ষেত্রফলের মধ্য দিয়ে x-ভরবেগ প্রবাহ।^[৪৫]

সান্দ্রতার প্রভাব সহ, একটি নিউটনীয় তরলের অসংকোচনীয় প্রবাহের জন্য ভরবেগ ভারসাম্যের সমীকরণ হলো:

\rho {\frac {D\mathbf {v} }{Dt}}=-{\boldsymbol {\nabla }}p+\mu \nabla ^{2}\mathbf {v} +\rho \mathbf {g} .\,

এগুলো নেভিয়ার-স্টোকস্‌ সমীকরণ নামে পরিচিত।^[৪৪]

ভরবেগ ভারসাম্য সমীকরণ অন্যান্য পদার্থ যেমন কঠিনের ক্ষেত্রেও প্রয়োগ করা যেতে পারে। $i$ দিকে নরমাল এবং $j$ দিকে লম্ব বিশিষ্ট প্রতিটি পৃষ্ঠের ক্ষেত্রে, একটি পীড়ন অংশক $σ ij$ থাকে। নয়টি উপাদান কোশি স্ট্রেস টেন্সর $σ$ , গঠন করে, চাপ এবং এই পীড়ন উভয়েই এর অন্তর্ভুক্ত। সীমিতভাবে ভরবেগ সংরক্ষণ কোশির ভরবেগ সমীকরণ দ্বারা প্রকাশ করা হয়:

\rho {\frac {D\mathbf {v} }{Dt}}={\boldsymbol {\nabla }}\cdot {\boldsymbol {\sigma }}+\mathbf {f} \,,

যেখানে $f$ হলো বস্তুর বডি ফোর্স বা সামগ্রিক বল।^[৪৬]

কোশির ভরবেগ সমীকরণ কঠিন এবং তরল পদার্থের বিকৃতির জন্য ব্যাপকভাবে প্রযোজ্য। পীড়ন এবং পীড়ন হারের মধ্যে সম্পর্ক পদার্থের উপাদানের বৈশিষ্ট্যের উপর নির্ভর করে (সান্দ্রতার প্রকারভেদ দেখুন)।

শব্দ তরঙ্গ

মাধ্যমের মধ্যে একটি বিশৃঙ্খলা, কম্পন বা তরঙ্গ তৈরী করে যা তাদের উৎস থেকে দূরে ছড়িয়ে যায়। তরলের ক্ষেত্রে, চাপ $p$ এর ছোট ছোট পরিবর্তন অ্যাকুস্টিক তরঙ্গ সমীকরণ দ্বারা ব্যাখ্যা করা যায়:

{\frac {\partial ^{2}p}{\partial t^{2}}}=c^{2}\nabla ^{2}p\,,

যেখানে $c$ হলো শব্দের বেগ। কঠিন পদার্থের ক্ষেত্রে, একই ধরনের সমীকরণ চাপ (পি-তরঙ্গ) এবং শিয়ার (এস-তরঙ্গ) ব্যবহার করে পাওয়া যায়।^[৪৭]

$v i$ বেগে ভরবেগ অংশক $ρv j$ এর জন্য ফ্লাক্স বা প্রতি একক ক্ষেত্রফলে প্রবাহের পরিমাণ হলো $ρ v j v j$ । যে সুশৃঙ্খল অনুমান উপর্যুক্ত অ্যাকুস্টিক সমীকরণের দিকে নিয়ে যায়, তাতে এই ফ্লাক্সের গড় সময় শূন্য। তবে, অন্যক্ষেত্রে এই গড়মান অশূন্য হতে পারে।^[৪৮] তরঙ্গের পরম ভরবেগ না থাকার পরেও, ভরবেগ ফ্লাক্স তৈরী হতে পারে।^[৪৯]

ধারণার ইতিহাস

৫৩০ খ্রিস্টাব্দে আলেকজান্দ্রিয়ায় কর্মরত বাইজেন্টাইন দার্শনিক জন ফিলোপোনাস, এরিস্টটলের পদার্থবিজ্ঞান গ্রন্থ সম্পর্কে তাঁর ভাষ্য প্রকাশকালে ভরবেগের একটি ধারণার বিকাশ ঘটান। অ্যারিস্টটল বলেছিলেন যে, গতিশীল সবকিছুই কোনো কিছুর দ্বারা গতিশীল হয়। যেমন, একটি নিক্ষিপ্ত বল বাতাসের গতি দ্বারা গতিশীল থাকবে। গ্যালিলিওর সময় পর্যন্ত অধিকাংশ লেখক, অ্যারিস্টটলের তত্ত্ব বজায় রাখে, কিন্তু তাদের মধ্যেও অনেকে এ ব্যাপারে সন্দিহান ছিল। ফিলোপোনাস, অ্যারিস্টটলের দাবির অযৌক্তিকতা নির্দেশ করেন যে অ্যারিস্টটলের তত্ব অনুযায়ী, যে বাতাস একটি বস্তুর গতিকে বাধাপ্রাপ্ত করে তাই আবার তাকে গতিশীল করে। তিনি এর বিকল্প হিসেবে প্রস্তাব করেন যে, বস্তু নিক্ষেপ করার সময়েই এতে একটি চালিকা শক্তি (ইমপিটাস) যুক্ত হয়।^[৫০] ইবনে সিনা ফিলোপোনাসের লেখা পড়েন এবং ১০২০ সালে তার কিতাবুশ শিফা গ্রন্থে গতি সম্পর্কে তার নিজস্ব তত্ত্ব প্রকাশ করেন। তিনি একমত হন যে নিক্ষেপকারী কর্তৃক বস্তুতে একটি চালিকা শক্তি যোগ হয়। কিন্তু ফিলোপোনাস বিশ্বাস করতেন যে, এটি একটি সাময়িক গুণ, যা এমনকি শূন্যস্থানেও নষ্ট হবে। অন্যদিকে ইবনে সিনা এটিকে একটি স্থায়ী ধর্ম বলেন, যার ক্ষয়ের জন্য বায়ুর বাধার ন্যায় বাহ্যিক শক্তি প্রয়োজন।^[৫১]^[৫২]^[৫৩] ইউরোপীয় দার্শনিক পিটার অলিভি এবং জঁ ব্যুরিদাঁ, ফিলোপোনাস এবং সম্ভবত ইবনে সিনার^[৫৩] লেখা পড়েন এবং তা পরিমার্জিত করেন। ব্যুরিদাঁ এই চালিকা শক্তিকে ওজন এবং বেগের গুণফলের সমানুপাতিক বলে উল্লেখ করেন। উপরন্তু, ব্যুরিদাঁর তত্ত্ব তার পূর্বসূরিগণের থেকে আলাদা ছিল কারণ তিনি এই চালিকা শক্তিকে স্ব-বিনাশী হিসেবে বিবেচনা করেননি, তিনি দাবি করেন যে চালিকা শক্তির বিরোধিতাকারী বায়ুর প্রতিরোধ বল এবং মাধ্যাকর্ষণ বল দ্বারা বস্তু আটকা পড়বে।^[৫৪]^[৫৫]

র‍্যনে দেকার্ত বিশ্বাস করতেন যে মহাবিশ্বে মোট "গতির পরিমাণ" সংরক্ষিত,^[৫৬] যেখানে গতির পরিমাণ বলতে আকার এবং বেগের গুণফলকে বোঝানো হয়। এটিকে ভরবেগের আধুনিক সূত্রের বিবৃতি হিসাবে পড়া উচিত নয়, যেহেতু ভর যে ওজন এবং আকার থেকে আলাদা সে সম্পর্কে তার কোনো ধারণাই ছিল না, এবং আরো তাৎপর্যপূর্ণ তথ্য হলো, তিনি বেগের বদলে দ্রুতি সংরক্ষিত বলে বিশ্বাস করতেন। তাই দেকার্তের হিসেবে, যদি একটি চলন্ত বস্তু পৃষ্ঠ থেকে তার গতি পরিবর্তন না করে শুধু দিক পরিবর্তন করে লাফিয়ে ওঠে, তবে এর গতির পরিমাণে কোন পরিবর্তন হবে না।^[৫৭]^[৫৮]^[৫৯] গ্যালিলিও, তার টু নিউ সাইন্সেস গ্রন্থে, দেকার্তের অনুরূপ গতির পরিমাপ বর্ণনা করতে ইতালীয় শব্দ ইমপেটো ব্যবহার করেন।

লাইব‌নিৎস তার "ডিসকোর্স অন মেটাফিজিক্স" গ্রন্থে দেকার্তের "গতির পরিমাণ" সংরক্ষণের বিরুদ্ধে যুক্তি দেখিয়েছেন বিভিন্ন দূরত্বে বিভিন্ন আকারের ব্লক ফেলে দেয়ার উদাহরণ ব্যবহার করে। তিনি দেখান যে, বল সংরক্ষিত থাকে কিন্তু বস্তুর আকার এবং দ্রুতির গুণফল হিসাবে বর্ণিত গতির পরিমাণ সংরক্ষিত থাকে না।^[৬০]

ক্রিস্টিয়ান হাইগেনস অনেক আগেই বলেন যে দুটি বস্তুর স্থিতিস্থাপক সংঘর্ষের জন্য দেকার্তের সূত্র অবশ্যই ভুল এবং তিনি সঠিক সূত্র প্রণয়ন করেন।^[৬১] তার একটি গুরুত্বপূর্ণ পদক্ষেপ ছিল এই সমস্যার ক্ষেত্রে গ্যালিলিয় আপেক্ষিকতাকে স্বীকৃতি দেওয়া।^[৬২] তবে তার অভিমত প্রচারিত হতে অনেক বছর লেগেছে। তিনি ব্যক্তিগতভাবে ১৬৬১ সালে উইলিয়াম ব্রুকার এবং ক্রিস্টোফার রেন এর কাছে লন্ডনে এগুলো হস্তান্তর করেন।^[৬৩] স্পিনোজা এগুলো সম্পর্কে হেনরি ওল্ডেনবার্গকে ১৬৬৬ সালে দ্বিতীয় অ্যাংলো-ডাচ যুদ্ধের সময় কী লিখেছিলেন তা সুরক্ষিত রাখা হয়।^[৬৪] হাইগেনস প্রকৃতপক্ষে ১৬৫২-৫৬ সময়কালে একটি পাণ্ডুলিপিতে এগুলো নিয়ে কাজ করেন। ১৬৬৭ সালে যুদ্ধ শেষ হয় এবং হাইগেনস ১৬৬৮ সালে রয়েল সোসাইটিতে তার কাজের ফলাফল ঘোষণা করেন। তিনি ১৬৬৯ সালে একটি জার্নালে তার কাজ প্রকাশিত করেন।^[৬৫]

ভরবেগ সংরক্ষণ সূত্রের প্রথম সঠিক বিবৃতি ইংরেজ গণিতবিদ জন ওয়ালিস ১৬৭০ সালে তার একটি গ্রন্থে প্রণয়ন করেন: "বস্তুর প্রাথমিক দশা, হয় স্থিতি বা গতি, অব্যাহত থাকবে" এবং "যদি বল বাধার চেয়ে বেশি হয়, ফলাফল হবে গতি"।^[৬৬] তিনি গতির পরিমাণ হিসেবে মোমেন্টাম বা ভরবেগ শব্দটির ব্যবহার করেন। ১৬৮৭ সালে প্রথম প্রকাশিত নিউটনের ফিলোসফিয়া ন্যাচারালিস প্রিন্সিপিয়া ম্যাথামেটিকা গ্রন্থে ভরবেগের জন্য অনুরূপ শব্দসমূহ ব্যবহার করা হয়। তার সংজ্ঞা II এ "গতির পরিমাণ" সম্পর্কে বলা হয়েছে, "সম্মিলিতভাবে পদার্থের বেগ ও পরিমাণ থেকে উদ্ভূত", তাই একে ভরবেগ হিসাবে চিহ্নিত করা যায়।^[৬৭] এ কারণে, যখন সূত্র II এ তিনি "গতির পরিবর্তন" কে প্রযুক্ত বলের সমানুপাতিক হিসেবে বর্ণনা করেন, তখন তিনি গতি নয় বরং ভরবেগের কথাই বলছেন বলে ধারণা করা হয়।^[৬৮] এক্ষেত্রে, শুধুমাত্র গতির পরিমাণ এর বদলে একটি আদর্শ শব্দ বরাদ্দ করা বাদ থাকে। সঠিক গাণিতিক অর্থে "ভরবেগ" এর প্রথম ব্যবহার সম্পর্কে স্পষ্ট ধারণা পাওয়া যায়না তবে ১৭২১ সালে জন জেনিংস এর মিসেলেনিয়া প্রকাশিত হওয়ার সময় অর্থাৎ নিউটনের প্রিন্সিপিয়া ম্যাথামেটিকার চূড়ান্ত সংস্করণের পাঁচ বছর পূর্বেই, ভরবেগ, M বা "গতির পরিমাণ" কে "একটি আয়তক্ষেত্র" হিসেবে সংজ্ঞায়িত করা হচ্ছিল, যে আয়তক্ষেত্র "উপাদানের পরিমাণ", $Q$ এবং বেগ, $V$ এর গুণফলের সমান। আর যেখানে $V$ এর মান, $+ s / t$ ।^[৬৯]

আরও দেখুন

তথ্যসূত্র

1 2 Feynman Vol. 1, Chapter 9
↑ "Euler's Laws of Motion"। সংগ্রহের তারিখ ৩০ মার্চ ২০০৯।
↑ McGill and King (১৯৯৫)। Engineering Mechanics, An Introduction to Dynamics (3rd সংস্করণ)। PWS Publishing Company। আইএসবিএন ০-৫৩৪-৯৩৩৯৯-৮।
↑ Plastino, Angel R.; Muzzio, Juan C. (১৯৯২)। "On the use and abuse of Newton's second law for variable mass problems"। Celestial Mechanics and Dynamical Astronomy। ৫৩ (3)। Netherlands: Kluwer Academic Publishers: ২২৭–২৩২। বিবকোড:1992CeMDA..53..227P। ডিওআই:10.1007/BF00052611। আইএসএসএন 0923-2958। "We may conclude emphasizing that Newton's second law is valid for constant mass only. When the mass varies due to accretion or ablation, [an alternate equation explicitly accounting for the changing mass] should be used."
1 2 3 4 5 6 7 Feynman, Richard P. (১৯৬৩–১৯৬৫)। The Feynman lectures on physics। Robert B. Leighton, Matthew L. Sands। Reading, Mass.: Addison-Wesley Pub. Co। আইএসবিএন ০-২০১-০২০১০-৬। ওসিএলসি 531535। {{বই উদ্ধৃতি}}: আইএসবিএন / তারিখের অসামঞ্জস্যতা (সাহায্য)উদ্ধৃতি শৈলী রক্ষণাবেক্ষণ: তারিখ বিন্যাস (লিঙ্ক)
↑ Ho-Kim, Q. (২০০৪)। Invitation to contemporary physics। N. Kumar, Harry C. S. Lam (2nd ed সংস্করণ)। Singapore: World Scientific। আইএসবিএন ৯৮১-২৩৮-৮৮৭-৭। ওসিএলসি 57252568। {{বই উদ্ধৃতি}}: |edition=-এ অতিরিক্ত লেখা রয়েছে (সাহায্য)
1 2 3 Goldstein, Herbert (১৯৮০)। Classical mechanics (2d ed সংস্করণ)। Reading, Mass.: Addison-Wesley Pub. Co। আইএসবিএন ০-২০১-০২৯১৮-৯। ওসিএলসি 5675073। {{বই উদ্ধৃতি}}: |edition=-এ অতিরিক্ত লেখা রয়েছে (সাহায্য)
↑ "Elastic and Inelastic Collisions"। web.archive.org। ১৮ আগস্ট ২০১২। ১৮ আগস্ট ২০১২ তারিখে মূল থেকে আর্কাইভকৃত। সংগ্রহের তারিখ ২৭ ফেব্রুয়ারি ২০২১।{{ওয়েব উদ্ধৃতি}}: উদ্ধৃতি শৈলী রক্ষণাবেক্ষণ: বট: মূল ইউআরএলের অবস্থা অজানা (লিঙ্ক)
↑ Serway, Raymond A. (২০১৩)। Principles of physics : a calculus-based text। John W. Jewett (5th ed সংস্করণ)। Boston, MA: Brooks/Cole, Cengage Learning। আইএসবিএন ৯৭৮-১-১৩৩-১০৪২৬-১। ওসিএলসি 744298475। {{বই উদ্ধৃতি}}: |edition=-এ অতিরিক্ত লেখা রয়েছে (সাহায্য)
↑ Rindler, Wolfgang (১৯৭৭)। Essential relativity : special, general, and cosmological (2d ed সংস্করণ)। New York: Springer-Verlag। পৃ. ২৬–২৭। আইএসবিএন ০-৩৮৭-০৭৯৭০-X। ওসিএলসি 2388497। {{বই উদ্ধৃতি}}: |edition=-এ অতিরিক্ত লেখা রয়েছে (সাহায্য)
1 2 Kleppner; Kolenkow. An Introduction to Mechanics. pp. 135–39.
↑ Rindler 1986, Chapter 2
↑ Feynman Vol. 1, Chapter 15-2
↑ Rindler 1986, পৃ. 77–81
↑ Rindler 1986, পৃ. 66
↑ Misner, Charles W. (১৯৭৩)। Gravitation। Kip S. Thorne, John Archibald Wheeler। New York। আইএসবিএন ০-৭১৬৭-০৩৩৪-৩। ওসিএলসি 585119।{{বই উদ্ধৃতি}}: উদ্ধৃতি শৈলী রক্ষণাবেক্ষণ: অবস্থানে প্রকাশক অনুপস্থিত (লিঙ্ক)
↑ Rindler 1986, পৃ. 86–87
↑ Rindler, Wolfgang (১৯৯১)। Introduction to special relativity (2nd ed সংস্করণ)। Oxford [England]: Clarendon Press। আইএসবিএন ০-১৯-৮৫৩৯৫৩-৩। ওসিএলসি 22490653। {{বই উদ্ধৃতি}}: |edition=-এ অতিরিক্ত লেখা রয়েছে (সাহায্য)
↑ Goldstein 1980, পৃ. 11–13
↑ Goldstein 1980, পৃ. 54–56
↑ Jackson 1975, পৃ. 574
↑ Feynman Vol. 3, Chapter 21-3
↑ Goldstein 1980, পৃ. 20–21
1 2 Lerner, Rita G.; Trigg, George L., সম্পাদকগণ (২০০৫)। Encyclopedia of physics (3rd সংস্করণ)। Weinheim: Wiley-VCH-Verl.। আইএসবিএন ৯৭৮-৩৫২৭৪০৫৫৪১।
↑ Goldstein 1980, পৃ. 341–342
↑ Goldstein 1980, পৃ. 348
↑ Hand, Louis N.; Finch, Janet D. (১৯৯৮)। Analytical mechanics (7th print সংস্করণ)। Cambridge: Cambridge University Press। Chapter ৪। আইএসবিএন ৯৭৮০৫২১৫৭৫৭২০।
↑ Witten, Edward (১৯৮১)। "A new proof of the positive energy theorem" (পিডিএফ)। ৮০ (3): ৩৮১–৪০২। বিবকোড:1981CMaPh..80..381W। ডিওআই:10.1007/BF01208277। আইএসএসএন 0010-3616। এস২সিআইডি 1035111। ২৫ নভেম্বর ২০১৬ তারিখে মূল থেকে (পিডিএফ) আর্কাইভকৃত। সংগ্রহের তারিখ ২৮ ফেব্রুয়ারি ২০২১। {{সাময়িকী উদ্ধৃতি}}: উদ্ধৃতি journal এর জন্য |journal= প্রয়োজন (সাহায্য)
↑ Grossman, Lisa (১৮ জানুয়ারি ২০১২)। "Death-defying time crystal could outlast the universe"। newscientist.com। New Scientist। ২ ফেব্রুয়ারি ২০১৭ তারিখে মূল থেকে আর্কাইভকৃত।
↑ Cowen, Ron (২৭ ফেব্রুয়ারি ২০১২)। ""Time Crystals" Could Be a Legitimate Form of Perpetual Motion"। scientificamerican.com। Scientific American। ২ ফেব্রুয়ারি ২০১৭ তারিখে মূল থেকে আর্কাইভকৃত।
↑ Powell, Devin (২০১৩)। "Can matter cycle through shapes eternally?"। Nature। ডিওআই:10.1038/nature.2013.13657। আইএসএসএন 1476-4687। এস২সিআইডি 181223762। ৩ ফেব্রুয়ারি ২০১৭ তারিখে মূল থেকে আর্কাইভকৃত।
↑ Gibney, Elizabeth (২০১৭)। "The quest to crystallize time"। Nature। ৫৪৩ (7644): ১৬৪–১৬৬। বিবকোড:2017Natur.543..164G। ডিওআই:10.1038/543164a। আইএসএসএন 0028-0836। পিএমআইডি 28277535। এস২সিআইডি 4460265। ১৩ মার্চ ২০১৭ তারিখে মূল থেকে আর্কাইভকৃত।
↑ Jackson 1975
↑ Semon, Mark D.; Taylor, John R. (নভেম্বর ১৯৯৬)। "Thoughts on the magnetic vector potential"। American Journal of Physics (ইংরেজি ভাষায়)। ৬৪ (11): ১৩৬১–১৩৬৯। বিবকোড:1996AmJPh..64.1361S। ডিওআই:10.1119/1.18400। আইএসএসএন 0002-9505।
↑ Griffiths, David J. (David Jeffery), 1942- (২৯ জুন ২০১৭)। Introduction to electrodynamics (Fourth সংস্করণ)। Cambridge, United Kingdom। আইএসবিএন ৯৭৮-১-১০৮-৪২০৪১-৯। ওসিএলসি 1021068059।{{বই উদ্ধৃতি}}: উদ্ধৃতি শৈলী রক্ষণাবেক্ষণ: অবস্থানে প্রকাশক অনুপস্থিত (লিঙ্ক) উদ্ধৃতি শৈলী রক্ষণাবেক্ষণ: একাধিক নাম: লেখকগণের তালিকা (লিঙ্ক) উদ্ধৃতি শৈলী রক্ষণাবেক্ষণ: সাংখ্যিক নাম: লেখকগণের তালিকা (লিঙ্ক)
↑ Vieira, R. S.; Brentan, H. B. (এপ্রিল ২০১৮)। "Covariant theory of gravitation in the framework of special relativity"। The European Physical Journal Plus (ইংরেজি ভাষায়)। ১৩৩ (4): ১৬৫। আরজাইভ:1608.00815। বিবকোড:2018EPJP..133..165V। ডিওআই:10.1140/epjp/i2018-11988-9। আইএসএসএন 2190-5444। এস২সিআইডি 16691128।
↑ Babson, David; Reynolds, Stephen P.; Bjorkquist, Robin; Griffiths, David J. (সেপ্টেম্বর ২০০৯)। "Hidden momentum, field momentum, and electromagnetic impulse"। American Journal of Physics (ইংরেজি ভাষায়)। ৭৭ (9): ৮২৬–৮৩৩। বিবকোড:2009AmJPh..77..826B। ডিওআই:10.1119/1.3152712। আইএসএসএন 0002-9505।
↑ Griffiths, David J. (২০১৩)। Introduction to electrodynamics (Fourth সংস্করণ)। Boston: Pearson। পৃ. ৩৬১। আইএসবিএন ৯৭৮-০৩২১৮৫৬৫৬২।
1 2 3 Jackson, John David (১৯৭৫)। Classical electrodynamics (2d ed সংস্করণ)। New York: Wiley। আইএসবিএন ০-৪৭১-৪৩১৩২-X। ওসিএলসি 1288487। {{বই উদ্ধৃতি}}: |edition=-এ অতিরিক্ত লেখা রয়েছে (সাহায্য)
↑ Feynman Vol. 1, Chapter 27-6
↑ Z.Y.Wang (২০১৬)। "Generalized momentum equation of quantum mechanics"। Optical and Quantum Electronics। ৪৮ (2): ১–৯। ডিওআই:10.1007/s11082-015-0261-8। এস২সিআইডি 124732329।
↑ Barnett, Stephen M. (২০১০)। "Resolution of the Abraham-Minkowski Dilemma" (পিডিএফ)। Physical Review Letters। ১০৪ (7): ০৭০৪০১। বিবকোড:2010PhRvL.104g0401B। ডিওআই:10.1103/PhysRevLett.104.070401। পিএমআইডি 20366861।
↑ Wang Zhong-Yue; Wang Pin-Yu; Xu Yan-Rong (২০১১)। "Crucial experiment to resolve Abraham-Minkowski Controversy"। Optik। ১২২ (22): ১৯৯৪–১৯৯৬। আরজাইভ:1103.3559। বিবকোড:2011Optik.122.1994W। ডিওআই:10.1016/j.ijleo.2010.12.018। এস২সিআইডি 119209160।
1 2 3 Tritton, D. J. (১৯৮৮)। Physical fluid dynamics (2nd ed সংস্করণ)। Oxford [England]: Clarendon Press। পৃ. ৫৮। আইএসবিএন ০-১৯-৮৫৪৪৯৩-৬। ওসিএলসি 17299123। {{বই উদ্ধৃতি}}: |edition=-এ অতিরিক্ত লেখা রয়েছে (সাহায্য)
↑ Bird, R. Byron (২০০২)। Transport phenomena। Warren E. Stewart, Edwin N. Lightfoot (2nd, Wiley international ed সংস্করণ)। New York: J. Wiley। আইএসবিএন ০-৪৭১-৪১০৭৭-২। ওসিএলসি 46456316। {{বই উদ্ধৃতি}}: |edition=-এ অতিরিক্ত লেখা রয়েছে (সাহায্য)
↑ Acheson, D. J. (১৯৯০)। Elementary fluid dynamics। Oxford: Clarendon Press। আইএসবিএন ০-১৯-৮৫৯৬৬০-X। ওসিএলসি 20296032।
↑ Gubbins, David (১৯৯০)। Seismology and plate tectonics। Cambridge [England]: Cambridge University Press। আইএসবিএন ০-৫২১-৩৭১৪১-৪। ওসিএলসি 20595005।
↑ LeBlond, Paul H. (১৯৭৮)। Waves in the ocean। Lawrence A. Mysak। Amsterdam: Elsevier Scientific Pub. Co.। আইএসবিএন ০-৪৪৪-৪১৬০২-১। ওসিএলসি 3543446।
↑ McIntyre, M.E. (১৯৮১)। "On the 'wave momentum' myth"। J. Fluid Mech.। ১০৬: ৩৩১–৩৪৭। বিবকোড:1981JFM...106..331M। ডিওআই:10.1017/s0022112081001626।
↑ Wildberg, Christian (২০১৮)। Zalta, Edward N. (সম্পাদক)। The Stanford Encyclopedia of Philosophy (Winter 2018 সংস্করণ)। Metaphysics Research Lab, Stanford University।
↑ Espinoza, Fernando (২০০৫)। "An analysis of the historical development of ideas about motion and its implications for teaching"। Physics Education। ৪০ (2): ১৪১। বিবকোড:2005PhyEd..40..139E। ডিওআই:10.1088/0031-9120/40/2/002।
↑ Seyyed Hossein Nasr & Mehdi Amin Razavi (১৯৯৬)। The Islamic intellectual tradition in Persia। Routledge। পৃ. ৭২। আইএসবিএন ৯৭৮-০-৭০০৭-০৩১৪-২।
1 2 Aydin Sayili (১৯৮৭)। "Ibn Sīnā and Buridan on the Motion of the Projectile"। Annals of the New York Academy of Sciences। ৫০০ (1): ৪৭৭–৪৮২। বিবকোড:1987NYASA.500..477S। ডিওআই:10.1111/j.1749-6632.1987.tb37219.x। এস২সিআইডি 84784804।
↑ T.F. Glick; S.J. Livesay; F. Wallis। "Buridian, John"। Medieval Science, Technology and Medicine:an Encyclopedia। পৃ. ১০৭।
↑ Park, David (১৯৯০)। The how and the why : an essay on the origins and development of physical theory। With drawings by Robin Brickman (3rd print সংস্করণ)। Princeton, NJ: Princeton University Press। পৃ. ১৩৯–১৪১। আইএসবিএন ৯৭৮০৬৯১০২৫০৮৭।
↑ Alexander Afriat, "Cartesian and Lagrangian Momentum" ওয়েব্যাক মেশিনে আর্কাইভকৃত ২০১৭-০৩-০৯ তারিখে (2004).
↑ Daniel Garber (১৯৯২)। "Descartes' Physics"। John Cottingham (সম্পাদক)। The Cambridge Companion to Descartes। Cambridge: Cambridge University Press। পৃ. ৩১০–৩১৯। আইএসবিএন ৯৭৮-০-৫২১-৩৬৬৯৬-০।
↑ Rothman, Milton A. (১৯৮৯)। Discovering the natural laws : the experimental basis of physics (2nd সংস্করণ)। New York: Dover Publications। পৃ. ৮৩–৮৮। আইএসবিএন ৯৭৮০৪৮৬২৬১৭৮২।
↑ Slowik, Edward (শরৎ ২০১৭)। "Descartes' Physics"। Zalta, Edward N. (সম্পাদক)। The Stanford Encyclopedia of Philosophy। সংগ্রহের তারিখ ২৯ নভেম্বর ২০১৯।
↑ Leibniz, Gottfried Wilhelm, Freiherr von (১৯৮৯)। Philosophical essays। Roger Ariew, Daniel Garber। Indianapolis। আইএসবিএন ০-৮৭২২০-০৬২-০। ওসিএলসি 18907466।{{বই উদ্ধৃতি}}: উদ্ধৃতি শৈলী রক্ষণাবেক্ষণ: অবস্থানে প্রকাশক অনুপস্থিত (লিঙ্ক) উদ্ধৃতি শৈলী রক্ষণাবেক্ষণ: একাধিক নাম: লেখকগণের তালিকা (লিঙ্ক)
↑ The Beginnings of Modern Science, edited by Rene Taton, Basic Books, 1958, 1964.
↑ Garber and Ayers, pp. 666–7.
↑ Garber and Ayers, p. 689.
↑ Jonathan I. Israel (৮ ফেব্রুয়ারি ২০০১)। Radical Enlightenment:Philosophy and the Making of Modernity 1650–1750। Oxford University Press। পৃ. lxii–lxiii। আইএসবিএন ৯৭৮-০-১৯-১৬২২৮৭-৮। সংগ্রহের তারিখ ১১ মে ২০১৩।
↑ Dictionary, p. 470.
↑ Scott, J. F. (১৯৮১)। The mathematical work of John Wallis, D.D., F.R.S., (1616-1703) (2nd ed সংস্করণ)। New York, N.Y.: Chelsea Pub. Co। আইএসবিএন ০-৮২৮৪-০৩১৪-৭। ওসিএলসি 7952719। {{বই উদ্ধৃতি}}: |edition=-এ অতিরিক্ত লেখা রয়েছে (সাহায্য)
↑ Grimsehl, Ernst (১৯৩২)। A Textbook of Physics। Translated by Leonard Ary Woodward। London & Glasgow: Blackie & Son limited। পৃ. ৭৮।
↑ Rescigno, Aldo (২০০৩)। Foundation of Pharmacokinetics। New York: Kluwer Academic/Plenum Publishers। পৃ. ১৯। আইএসবিএন ৯৭৮-০৩০৬৪৭৭০৪১।
↑ Jennings, John (১৭২১)। Miscellanea in Usum Juventutis Academicae। Northampton: R. Aikes & G. Dicey। পৃ. ৬৭।

গ্রন্থপঞ্জি

Halliday, David; Resnick, Robert (২০০১)। Fundamentals of Physics। John Wiley & Sons। Chapter ৯। {{বই উদ্ধৃতি}}: অজানা প্যারামিটার |nopp= উপেক্ষা করা হয়েছে (|no-pp= প্রস্তাবিত) (সাহায্য)
Dugas, René (১৯৮৮)। A history of mechanics। Translated into English by J.R. Maddox (Dover সংস্করণ)। New York: Dover Publications। আইএসবিএন ৯৭৮০৪৮৬৬৫৬৩২৮।
Feynman, Richard P.; Leighton, Robert B.; Sands, Matthew (২০০৫)। The Feynman lectures on physics, Volume 1: Mainly Mechanics, Radiation, and Heat (Definitive সংস্করণ)। San Francisco, California: Pearson Addison-Wesley। আইএসবিএন ৯৭৮-০৮০৫৩৯০৪৬৯।
Feynman, Richard P.; Leighton, Robert B.; Sands, Matthew (২০০৫)। The Feynman lectures on physics, Volume III: Quantum Mechanics (Definitive সংস্করণ)। New York: BasicBooks। আইএসবিএন ৯৭৮-০৮০৫৩৯০৪৯০।
Goldstein, Herbert (১৯৮০)। Classical mechanics (2nd সংস্করণ)। Reading, Mass.: Addison-Wesley Pub. Co.। আইএসবিএন ০২০১০২৯১৮৯।
Hand, Louis N.; Finch, Janet D. (১৯৯৮)। Analytical Mechanics। Cambridge University Press। Chapter ৪। {{বই উদ্ধৃতি}}: অজানা প্যারামিটার |nopp= উপেক্ষা করা হয়েছে (|no-pp= প্রস্তাবিত) (সাহায্য)
Jackson, John David (১৯৭৫)। Classical electrodynamics (2nd সংস্করণ)। New York: Wiley। আইএসবিএন ০৪৭১৪৩১৩২X।
Jammer, Max (১৯৯৯)। Concepts of force : a study in the foundations of dynamics (Facsim সংস্করণ)। Mineola, New York: Dover Publications। আইএসবিএন ৯৭৮০৪৮৬৪০৬৮৯৩।
Landau, L.D.; Lifshitz, E.M. (২০০০)। The classical theory of fields। English edition, reprinted with corrections; translated from the Russian by Morton Hamermesh (4th সংস্করণ)। Oxford: Butterworth Heinemann। আইএসবিএন ৯৭৮০৭৫০৬২৭৬৮৯। {{বই উদ্ধৃতি}}: উদ্ধৃতিতে খালি অজানা প্যারামিটার রয়েছে: |1= (সাহায্য)
Rindler, Wolfgang (১৯৮৬)। Essential Relativity : Special, general and cosmological (2nd সংস্করণ)। New York u.a.: Springer। আইএসবিএন ০৩৮৭১০০৯০৩।
Serway, Raymond; Jewett, John (২০০৩)। Physics for Scientists and Engineers (6th সংস্করণ)। Brooks Cole.। আইএসবিএন ০-৫৩৪-৪০৮৪২-৭।
Stenger, Victor J. (২০০০)। Timeless Reality: Symmetry, Simplicity, and Multiple Universes। Prometheus Books.। পৃ. Chapter ১২ in particular।
Tipler, Paul (১৯৯৮)। Physics for Scientists and Engineers: Vol. 1: Mechanics, Oscillations and Waves, Thermodynamics (4th সংস্করণ)। W. H. Freeman। আইএসবিএন ১-৫৭২৫৯-৪৯২-৬। {{বই উদ্ধৃতি}}: অবৈধ |সূত্র=harv (সাহায্য)
Tritton, D.J. (২০০৬)। Physical fluid dynamics (2nd সংস্করণ)। Oxford: Claredon Press। পৃ. ৫৮। আইএসবিএন ০১৯৮৫৪৪৯৩৬।

বহিঃসংযোগ

Conservation of momentum ওয়েব্যাক মেশিনে আর্কাইভকৃত ২৮ ফেব্রুয়ারি ২০০৯ তারিখে - অনলাইন পাঠ্যবইয়ে ভরবেগের উপরে একটি অধ্যায়।

[FeynmanCh9-1] 1 2 Feynman Vol. 1, Chapter 9

[BookRags-2] "Euler's Laws of Motion"। সংগ্রহের তারিখ ৩০ মার্চ ২০০৯।

[McGillKing-3] McGill and King (১৯৯৫)। Engineering Mechanics, An Introduction to Dynamics (3rd সংস্করণ)। PWS Publishing Company। আইএসবিএন ০-৫৩৪-৯৩৩৯৯-৮।

[plastino-4] Plastino, Angel R.; Muzzio, Juan C. (১৯৯২)। "On the use and abuse of Newton's second law for variable mass problems"। Celestial Mechanics and Dynamical Astronomy। ৫৩ (3)। Netherlands: Kluwer Academic Publishers: ২২৭–২৩২। বিবকোড:1992CeMDA..53..227P। ডিওআই:10.1007/BF00052611। আইএসএসএন 0923-2958। "We may conclude emphasizing that Newton's second law is valid for constant mass only. When the mass varies due to accretion or ablation, [an alternate equation explicitly accounting for the changing mass] should be used."

[:0-5] 1 2 3 4 5 6 7 Feynman, Richard P. (১৯৬৩–১৯৬৫)। The Feynman lectures on physics। Robert B. Leighton, Matthew L. Sands। Reading, Mass.: Addison-Wesley Pub. Co। আইএসবিএন ০-২০১-০২০১০-৬। ওসিএলসি 531535। {{বই উদ্ধৃতি}}: আইএসবিএন / তারিখের অসামঞ্জস্যতা (সাহায্য)উদ্ধৃতি শৈলী রক্ষণাবেক্ষণ: তারিখ বিন্যাস (লিঙ্ক)

[6] Ho-Kim, Q. (২০০৪)। Invitation to contemporary physics। N. Kumar, Harry C. S. Lam (2nd ed সংস্করণ)। Singapore: World Scientific। আইএসবিএন ৯৮১-২৩৮-৮৮৭-৭। ওসিএলসি 57252568। {{বই উদ্ধৃতি}}: |edition=-এ অতিরিক্ত লেখা রয়েছে (সাহায্য)

[:2-7] 1 2 3 Goldstein, Herbert (১৯৮০)। Classical mechanics (2d ed সংস্করণ)। Reading, Mass.: Addison-Wesley Pub. Co। আইএসবিএন ০-২০১-০২৯১৮-৯। ওসিএলসি 5675073। {{বই উদ্ধৃতি}}: |edition=-এ অতিরিক্ত লেখা রয়েছে (সাহায্য)

[8] "Elastic and Inelastic Collisions"। web.archive.org। ১৮ আগস্ট ২০১২। ১৮ আগস্ট ২০১২ তারিখে মূল থেকে আর্কাইভকৃত। সংগ্রহের তারিখ ২৭ ফেব্রুয়ারি ২০২১।{{ওয়েব উদ্ধৃতি}}: উদ্ধৃতি শৈলী রক্ষণাবেক্ষণ: বট: মূল ইউআরএলের অবস্থা অজানা (লিঙ্ক)

[9] Serway, Raymond A. (২০১৩)। Principles of physics : a calculus-based text। John W. Jewett (5th ed সংস্করণ)। Boston, MA: Brooks/Cole, Cengage Learning। আইএসবিএন ৯৭৮-১-১৩৩-১০৪২৬-১। ওসিএলসি 744298475। {{বই উদ্ধৃতি}}: |edition=-এ অতিরিক্ত লেখা রয়েছে (সাহায্য)

[10] Rindler, Wolfgang (১৯৭৭)। Essential relativity : special, general, and cosmological (2d ed সংস্করণ)। New York: Springer-Verlag। পৃ. ২৬–২৭। আইএসবিএন ০-৩৮৭-০৭৯৭০-X। ওসিএলসি 2388497। {{বই উদ্ধৃতি}}: |edition=-এ অতিরিক্ত লেখা রয়েছে (সাহায্য)

[:1-11] 1 2 Kleppner; Kolenkow. An Introduction to Mechanics. pp. 135–39.

[RindlerCh22-12] Rindler 1986, Chapter 2

[FeynmanCh152-13] Feynman Vol. 1, Chapter 15-2

[Rindler2-14] Rindler 1986, পৃ. 77–81

[15] Rindler 1986, পৃ. 66

[16] Misner, Charles W. (১৯৭৩)। Gravitation। Kip S. Thorne, John Archibald Wheeler। New York। আইএসবিএন ০-৭১৬৭-০৩৩৪-৩। ওসিএলসি 585119।{{বই উদ্ধৃতি}}: উদ্ধৃতি শৈলী রক্ষণাবেক্ষণ: অবস্থানে প্রকাশক অনুপস্থিত (লিঙ্ক)

[17] Rindler 1986, পৃ. 86–87

[18] Rindler, Wolfgang (১৯৯১)। Introduction to special relativity (2nd ed সংস্করণ)। Oxford [England]: Clarendon Press। আইএসবিএন ০-১৯-৮৫৩৯৫৩-৩। ওসিএলসি 22490653। {{বই উদ্ধৃতি}}: |edition=-এ অতিরিক্ত লেখা রয়েছে (সাহায্য)

[19] Goldstein 1980, পৃ. 11–13

[Goldstein543-20] Goldstein 1980, পৃ. 54–56

[21] Jackson 1975, পৃ. 574

[FeynmanQM-22] Feynman Vol. 3, Chapter 21-3

[23] Goldstein 1980, পৃ. 20–21

[Lerner2-24] 1 2 Lerner, Rita G.; Trigg, George L., সম্পাদকগণ (২০০৫)। Encyclopedia of physics (3rd সংস্করণ)। Weinheim: Wiley-VCH-Verl.। আইএসবিএন ৯৭৮-৩৫২৭৪০৫৫৪১।

[25] Goldstein 1980, পৃ. 341–342

[26] Goldstein 1980, পৃ. 348

[27] Hand, Louis N.; Finch, Janet D. (১৯৯৮)। Analytical mechanics (7th print সংস্করণ)। Cambridge: Cambridge University Press। Chapter ৪। আইএসবিএন ৯৭৮০৫২১৫৭৫৭২০।

[28] Witten, Edward (১৯৮১)। "A new proof of the positive energy theorem" (পিডিএফ)। ৮০ (3): ৩৮১–৪০২। বিবকোড:1981CMaPh..80..381W। ডিওআই:10.1007/BF01208277। আইএসএসএন 0010-3616। এস২সিআইডি 1035111। ২৫ নভেম্বর ২০১৬ তারিখে মূল থেকে (পিডিএফ) আর্কাইভকৃত। সংগ্রহের তারিখ ২৮ ফেব্রুয়ারি ২০২১। {{সাময়িকী উদ্ধৃতি}}: উদ্ধৃতি journal এর জন্য |journal= প্রয়োজন (সাহায্য)

[Grossman_2012-29] Grossman, Lisa (১৮ জানুয়ারি ২০১২)। "Death-defying time crystal could outlast the universe"। newscientist.com। New Scientist। ২ ফেব্রুয়ারি ২০১৭ তারিখে মূল থেকে আর্কাইভকৃত।

[Cowen_2012-30] Cowen, Ron (২৭ ফেব্রুয়ারি ২০১২)। ""Time Crystals" Could Be a Legitimate Form of Perpetual Motion"। scientificamerican.com। Scientific American। ২ ফেব্রুয়ারি ২০১৭ তারিখে মূল থেকে আর্কাইভকৃত।

[Powell_2013-31] Powell, Devin (২০১৩)। "Can matter cycle through shapes eternally?"। Nature। ডিওআই:10.1038/nature.2013.13657। আইএসএসএন 1476-4687। এস২সিআইডি 181223762। ৩ ফেব্রুয়ারি ২০১৭ তারিখে মূল থেকে আর্কাইভকৃত।

[Gibney_2017-32] Gibney, Elizabeth (২০১৭)। "The quest to crystallize time"। Nature। ৫৪৩ (7644): ১৬৪–১৬৬। বিবকোড:2017Natur.543..164G। ডিওআই:10.1038/543164a। আইএসএসএন 0028-0836। পিএমআইডি 28277535। এস২সিআইডি 4460265। ১৩ মার্চ ২০১৭ তারিখে মূল থেকে আর্কাইভকৃত।

[33] Jackson 1975

[34] Semon, Mark D.; Taylor, John R. (নভেম্বর ১৯৯৬)। "Thoughts on the magnetic vector potential"। American Journal of Physics (ইংরেজি ভাষায়)। ৬৪ (11): ১৩৬১–১৩৬৯। বিবকোড:1996AmJPh..64.1361S। ডিওআই:10.1119/1.18400। আইএসএসএন 0002-9505।

[35] Griffiths, David J. (David Jeffery), 1942- (২৯ জুন ২০১৭)। Introduction to electrodynamics (Fourth সংস্করণ)। Cambridge, United Kingdom। আইএসবিএন ৯৭৮-১-১০৮-৪২০৪১-৯। ওসিএলসি 1021068059।{{বই উদ্ধৃতি}}: উদ্ধৃতি শৈলী রক্ষণাবেক্ষণ: অবস্থানে প্রকাশক অনুপস্থিত (লিঙ্ক) উদ্ধৃতি শৈলী রক্ষণাবেক্ষণ: একাধিক নাম: লেখকগণের তালিকা (লিঙ্ক) উদ্ধৃতি শৈলী রক্ষণাবেক্ষণ: সাংখ্যিক নাম: লেখকগণের তালিকা (লিঙ্ক)

[36] Vieira, R. S.; Brentan, H. B. (এপ্রিল ২০১৮)। "Covariant theory of gravitation in the framework of special relativity"। The European Physical Journal Plus (ইংরেজি ভাষায়)। ১৩৩ (4): ১৬৫। আরজাইভ:1608.00815। বিবকোড:2018EPJP..133..165V। ডিওআই:10.1140/epjp/i2018-11988-9। আইএসএসএন 2190-5444। এস২সিআইডি 16691128।

[37] Babson, David; Reynolds, Stephen P.; Bjorkquist, Robin; Griffiths, David J. (সেপ্টেম্বর ২০০৯)। "Hidden momentum, field momentum, and electromagnetic impulse"। American Journal of Physics (ইংরেজি ভাষায়)। ৭৭ (9): ৮২৬–৮৩৩। বিবকোড:2009AmJPh..77..826B। ডিওআই:10.1119/1.3152712। আইএসএসএন 0002-9505।

[Griffiths-38] Griffiths, David J. (২০১৩)। Introduction to electrodynamics (Fourth সংস্করণ)। Boston: Pearson। পৃ. ৩৬১। আইএসবিএন ৯৭৮-০৩২১৮৫৬৫৬২।

[:3-39] 1 2 3 Jackson, John David (১৯৭৫)। Classical electrodynamics (2d ed সংস্করণ)। New York: Wiley। আইএসবিএন ০-৪৭১-৪৩১৩২-X। ওসিএলসি 1288487। {{বই উদ্ধৃতি}}: |edition=-এ অতিরিক্ত লেখা রয়েছে (সাহায্য)

[FeynmanCh273-40] Feynman Vol. 1, Chapter 27-6

[41] Z.Y.Wang (২০১৬)। "Generalized momentum equation of quantum mechanics"। Optical and Quantum Electronics। ৪৮ (2): ১–৯। ডিওআই:10.1007/s11082-015-0261-8। এস২সিআইডি 124732329।

[42] Barnett, Stephen M. (২০১০)। "Resolution of the Abraham-Minkowski Dilemma" (পিডিএফ)। Physical Review Letters। ১০৪ (7): ০৭০৪০১। বিবকোড:2010PhRvL.104g0401B। ডিওআই:10.1103/PhysRevLett.104.070401। পিএমআইডি 20366861।

[43] Wang Zhong-Yue; Wang Pin-Yu; Xu Yan-Rong (২০১১)। "Crucial experiment to resolve Abraham-Minkowski Controversy"। Optik। ১২২ (22): ১৯৯৪–১৯৯৬। আরজাইভ:1103.3559। বিবকোড:2011Optik.122.1994W। ডিওআই:10.1016/j.ijleo.2010.12.018। এস২সিআইডি 119209160।

[:4-44] 1 2 3 Tritton, D. J. (১৯৮৮)। Physical fluid dynamics (2nd ed সংস্করণ)। Oxford [England]: Clarendon Press। পৃ. ৫৮। আইএসবিএন ০-১৯-৮৫৪৪৯৩-৬। ওসিএলসি 17299123। {{বই উদ্ধৃতি}}: |edition=-এ অতিরিক্ত লেখা রয়েছে (সাহায্য)

[45] Bird, R. Byron (২০০২)। Transport phenomena। Warren E. Stewart, Edwin N. Lightfoot (2nd, Wiley international ed সংস্করণ)। New York: J. Wiley। আইএসবিএন ০-৪৭১-৪১০৭৭-২। ওসিএলসি 46456316। {{বই উদ্ধৃতি}}: |edition=-এ অতিরিক্ত লেখা রয়েছে (সাহায্য)

[46] Acheson, D. J. (১৯৯০)। Elementary fluid dynamics। Oxford: Clarendon Press। আইএসবিএন ০-১৯-৮৫৯৬৬০-X। ওসিএলসি 20296032।

[47] Gubbins, David (১৯৯০)। Seismology and plate tectonics। Cambridge [England]: Cambridge University Press। আইএসবিএন ০-৫২১-৩৭১৪১-৪। ওসিএলসি 20595005।

[48] LeBlond, Paul H. (১৯৭৮)। Waves in the ocean। Lawrence A. Mysak। Amsterdam: Elsevier Scientific Pub. Co.। আইএসবিএন ০-৪৪৪-৪১৬০২-১। ওসিএলসি 3543446।

[49] McIntyre, M.E. (১৯৮১)। "On the 'wave momentum' myth"। J. Fluid Mech.। ১০৬: ৩৩১–৩৪৭। বিবকোড:1981JFM...106..331M। ডিওআই:10.1017/s0022112081001626।

[50] Wildberg, Christian (২০১৮)। Zalta, Edward N. (সম্পাদক)। The Stanford Encyclopedia of Philosophy (Winter 2018 সংস্করণ)। Metaphysics Research Lab, Stanford University।

[Espinoza-51] Espinoza, Fernando (২০০৫)। "An analysis of the historical development of ideas about motion and its implications for teaching"। Physics Education। ৪০ (2): ১৪১। বিবকোড:2005PhyEd..40..139E। ডিওআই:10.1088/0031-9120/40/2/002।

[Nasr-52] Seyyed Hossein Nasr & Mehdi Amin Razavi (১৯৯৬)। The Islamic intellectual tradition in Persia। Routledge। পৃ. ৭২। আইএসবিএন ৯৭৮-০-৭০০৭-০৩১৪-২।

[Sayili-53] 1 2 Aydin Sayili (১৯৮৭)। "Ibn Sīnā and Buridan on the Motion of the Projectile"। Annals of the New York Academy of Sciences। ৫০০ (1): ৪৭৭–৪৮২। বিবকোড:1987NYASA.500..477S। ডিওআই:10.1111/j.1749-6632.1987.tb37219.x। এস২সিআইডি 84784804।

[54] T.F. Glick; S.J. Livesay; F. Wallis। "Buridian, John"। Medieval Science, Technology and Medicine:an Encyclopedia। পৃ. ১০৭।

[Park-55] Park, David (১৯৯০)। The how and the why : an essay on the origins and development of physical theory। With drawings by Robin Brickman (3rd print সংস্করণ)। Princeton, NJ: Princeton University Press। পৃ. ১৩৯–১৪১। আইএসবিএন ৯৭৮০৬৯১০২৫০৮৭।

[56] Alexander Afriat, "Cartesian and Lagrangian Momentum" ওয়েব্যাক মেশিনে আর্কাইভকৃত ২০১৭-০৩-০৯ তারিখে (2004).

[57] Daniel Garber (১৯৯২)। "Descartes' Physics"। John Cottingham (সম্পাদক)। The Cambridge Companion to Descartes। Cambridge: Cambridge University Press। পৃ. ৩১০–৩১৯। আইএসবিএন ৯৭৮-০-৫২১-৩৬৬৯৬-০।

[58] Rothman, Milton A. (১৯৮৯)। Discovering the natural laws : the experimental basis of physics (2nd সংস্করণ)। New York: Dover Publications। পৃ. ৮৩–৮৮। আইএসবিএন ৯৭৮০৪৮৬২৬১৭৮২।

[59] Slowik, Edward (শরৎ ২০১৭)। "Descartes' Physics"। Zalta, Edward N. (সম্পাদক)। The Stanford Encyclopedia of Philosophy। সংগ্রহের তারিখ ২৯ নভেম্বর ২০১৯।

[60] Leibniz, Gottfried Wilhelm, Freiherr von (১৯৮৯)। Philosophical essays। Roger Ariew, Daniel Garber। Indianapolis। আইএসবিএন ০-৮৭২২০-০৬২-০। ওসিএলসি 18907466।{{বই উদ্ধৃতি}}: উদ্ধৃতি শৈলী রক্ষণাবেক্ষণ: অবস্থানে প্রকাশক অনুপস্থিত (লিঙ্ক) উদ্ধৃতি শৈলী রক্ষণাবেক্ষণ: একাধিক নাম: লেখকগণের তালিকা (লিঙ্ক)

[61] The Beginnings of Modern Science, edited by Rene Taton, Basic Books, 1958, 1964.

[62] Garber and Ayers, pp. 666–7.

[63] Garber and Ayers, p. 689.

[Israel20012-64] Jonathan I. Israel (৮ ফেব্রুয়ারি ২০০১)। Radical Enlightenment:Philosophy and the Making of Modernity 1650–1750। Oxford University Press। পৃ. lxii–lxiii। আইএসবিএন ৯৭৮-০-১৯-১৬২২৮৭-৮। সংগ্রহের তারিখ ১১ মে ২০১৩।

[65] Dictionary, p. 470.

[66] Scott, J. F. (১৯৮১)। The mathematical work of John Wallis, D.D., F.R.S., (1616-1703) (2nd ed সংস্করণ)। New York, N.Y.: Chelsea Pub. Co। আইএসবিএন ০-৮২৮৪-০৩১৪-৭। ওসিএলসি 7952719। {{বই উদ্ধৃতি}}: |edition=-এ অতিরিক্ত লেখা রয়েছে (সাহায্য)

[67] Grimsehl, Ernst (১৯৩২)। A Textbook of Physics। Translated by Leonard Ary Woodward। London & Glasgow: Blackie & Son limited। পৃ. ৭৮।

[68] Rescigno, Aldo (২০০৩)। Foundation of Pharmacokinetics। New York: Kluwer Academic/Plenum Publishers। পৃ. ১৯। আইএসবিএন ৯৭৮-০৩০৬৪৭৭০৪১।

[69] Jennings, John (১৭২১)। Miscellanea in Usum Juventutis Academicae। Northampton: R. Aikes & G. Dicey। পৃ. ৬৭।

[১]

[২]

[৩]

[৪]

[৫]

[৬]

[৭]

[৮]

[৯]

[১০]

[১১]

[১২]

[১৩]

[১৪]

[১৫]

[১৬]

[১৭]

[১৮]

[১৯]

[২০]

[২১]

[২২]

[২৩]

[২৪]

[২৫]

[২৬]

[২৭]

[২৮]

[২৯]

[৩০]

[৩১]

[৩২]

[৩৩]

[৩৪]

[৩৫]

[৩৬]

[৩৭]

[৩৮]

[৩৯]

[৪০]

[৪১]

[৪২]

[৪৩]

[৪৪]

[৪৫]

[৪৬]

[৪৭]

[৪৮]

[৪৯]

[৫০]

[৫১]

[৫২]

[৫৩]

[৫৪]

[৫৫]

[৫৬]

[৫৭]

[৫৮]

[৫৯]

[৬০]

[৬১]

[৬২]

[৬৩]

[৬৪]

[৬৫]

[৬৬]

[৬৭]

[৬৮]

[৬৯]