গতির সমীকরণসমূহ

পদার্থবিজ্ঞানে যেসব সমীকরণ দ্বারা কোন ভৌত ব্যবস্থার গতিকে সময়ের ফাংশনরূপে উপস্থাপনের মাধ্যমে ঐ ভৌত ব্যবস্থাটির আচরণ বর্ণনা করা হয় তাদেরকেই গতির সমীকরণ বলা হয়।[১] বিশদভাবে বলা যায়, গতির সমীকরণসমূহ ভৌত ব্যবস্থার আচরণকে বিভিন্ন গতীয় (dynamic) চলকের গাণিতিক ফাংশনের সেটরূপে বর্ণনা করে যেখানে গতীয় চলক হিসেবে সচরাচর অবস্থানাঙ্ক ও সময় ব্যবহার করা হয়, তবে ভরবেগ-উপাংশ ও সময়ের ন্যায় অন্যান্য গতীয় চলকও ব্যবহার করা যায়। এক্ষেত্রে ভৌত ব্যবস্থার যে কোন সুবিধাজনক বৈশিষ্ট্যসম্পন্ন চলকের ন্যায় সাধারণীকৃত স্থানাঙ্কসমূহ ব্যবহারের জন্য সচরাচর অধিকহারে বাছাই করা হয়।[২] সংক্ষেপে বলা যায়, গতির চলকগুলোকে সমীকৃত করে প্রাপ্ত সমীকরণই গতির সমীকরণ। চিরায়ত বলবিদ্যার আলোকে কোন ফাংশনকে ব্যাখ্যার ক্ষেত্রে একে ইউক্লিডীয় স্থানের মাধ্যমে সংজ্ঞায়িত করা হলেও আপেক্ষিকতা সম্পর্কিত আলোচনায় একে বক্র স্থান দ্বারা প্রতিস্থাপন করা হয়। যদি একটি সিস্টেমের গতিবিদ্যা জানা থাকে তবে ব্যবস্থাটির গতিবিদ্যার গতি বর্ণনাকারী ব্যবকলনী সমীকরণগুলোর জন্য যে সমাধানগুলো পাওয়া যায় সেগুলোই হবে এর গতির সমীকরণ।
ধরন[সম্পাদনা]
পদার্থবিজ্ঞানে গতি সংক্রান্ত প্রধান দুই ধরনের আলোচনা রয়েছে—গতিবিদ্যা ও সৃতিবিদ্যা। গতিবিদ্যায় বলের ক্রিয়াধীন বস্তুর গতি আলোচনা করা হয়। কণার ভরবেগ, বল, শক্তি ইত্যাদি এই সাধারণ শাখার আলোচনার বিষয় বস্তু। এক্ষেত্রে গতিবিদ্যা পরিভাষাটি যেমন কখনো কখনো সিস্টেমের জন্য সন্তোষজনক ব্যবকলনী সমীকরণসমূহকে বুঝিয়ে থাকে (যেমন: নিউটনের দ্বিতীয় গতিসূত্র অথবা অয়লার-ল্যাগ্রাঞ্জ সমীকরণসমূহ), তেমনই আবার এটি কখনো কখনো ঐ সমীকরণসমূহের সমাধানগুলোকেও বুঝিয়ে থাকে।
যাই হোক, উপর্যুক্ত শাখা দুটির মধ্যে সৃতিবিদ্যা সরলতর। এতে গতির কারণ আলোচনা না করে গতির বৈশিষ্ট্য (বস্তুর অবস্থান ও সময় সম্পর্কিত চলক তথা বস্তুর অবস্থানের পরিবর্তন) নিয়ে আলোচনা করা হয়। সৃতিবিদ্যা এমনই এক সাধারণ শাখা যা কেবলমাত্র বস্তুর অবস্থান ও সময় থেকে প্রতিপাদিত চলকসমূহের সাথে সম্পর্কযুক্ত। ধ্রুব ত্বরণের ক্ষেত্রে সরণ s, আদি বেগ u, শেষ বেগ v, ত্বরণ a ও সময় t সৃতিবিদ্যার এই পাঁচটি রাশির সংজ্ঞা থেকে প্রতিপাদিত এই সরলতম সমীকরণগুলোকে একত্রে suvat সমীকরণ বলা হয়।
একারণে গতির সমীকরণসমূহকে গতির শ্রেণিবিন্যাসকারী এসব প্রধান বিষয়ের অধীনে বিন্যস্ত করা যেতে পারে। সকল ক্ষেত্রে গতিকে মূলত জ্যামিতিক অনুবাদ, ঘূর্ণন, স্পন্দন অথবা এদের সমন্বিত রূপ হিসেবেই দেখা যায়। ইউক্লিডীয় জ্যামিতিতে অনুবাদ হল এক প্রকার জ্যামিতিক রূপান্তর যেখানে কোন ফিগার বা স্থানের প্রতিটি বিন্দু একটি নির্দিষ্ট দিক বরাবর গতিশীল।
কোন সমস্যার জন্য একটি সমীকরণ নির্ধারণের নিমিত্তে, সচরাচর ভৌত রাশিসমূহের ভৌত নিয়মাবলী ও প্রযোজক সংজ্ঞা হিসেবে চিহ্নিত এমন কোন গতীয় ব্যবকলনী সমীকরণ ব্যবহার করা হয়ে থাকে। এই ব্যবকলনী সমীকরণের সমাধান করলে এক গুচ্ছ স্বেচ্ছাধীন সমাধানের অনুরূপ, এর একটি স্বাধীন ধ্রুবকযুক্ত সাধারণ সমাধান পাওয়া যায়। প্রাথমিক মানসমূহ নির্ধারণ করে দেওয়া হলে একটি নির্দিষ্ট সমাধান পাওয়া যেতে পারে, যা থেকে ধ্রুবকসমূহের মান নিরূপণ করা যাবে।
যথাযথভাবে বলতে গেলে, কোন বস্তুর গতির সমীকরণ M হল সচরাচর এর অবস্থান r, বেগ v, ত্বরণ a এবং সময় t এর একটি ফাংশন; যেখানে বেগ হল সময় t এর সাপেক্ষে অবস্থান r এর প্রথম অন্তরজ বা ডেরিভেটিভ, অর্থাৎ বেগ v = +dr/dt এবং ত্বরণ হল r এর দ্বিতীয় ডেরিভেটিভ, অর্থাৎ ত্বরণ a = +d২r/dt২। ত্রিমাত্রিক কাঠামোয় ইউক্লিডীয় ভেক্টরকে মোটা হরফ দ্বারা নির্দেশ করা হয়। r এর গতীয় সমীকরণটিকে, r এর দ্বিতীয় ক্রমের নিম্নোক্ত সাধারণ ব্যবকলনী সমীকরণের সমতূল্য বলা যায়—
- ,
এখানে t হল সময়। r এর উপর একটি ডট দ্বারা সময়ের সাপেক্ষে প্রথম ডেরিভেটিভ এবং দুটি ডট দ্বারা সময়ের সাপেক্ষে দ্বিতীয় ডেরিভেটিভ বোঝানো হয়েছে। t = 0 এ প্রাপ্ত , ধ্রুব মানগুলোর মাধ্যমে প্রাথমিক শর্তগুলো আরোপ করা হয়ে থাকে।
বিশেষায়িত প্রাথমিক মান দিয়ে, গতির সমীকরণের r(t) এর সমাধান হতে t = 0 অনুযায়ী সকল t সময়ের জন্য সিস্টেমের ব্যাখ্যা পাওয়া যায়। t সময়ে বস্তুর অবস্থান r অদ্যাবধি সর্বাধিক কাঙ্ক্ষিত রাশি হওয়া সত্ত্বেও, গতির কিছু সমীকরণের সমাধানের জন্য r এর পরিবর্তে ভরবেগ p'র মত গতীয় (dynamical) চলককে অথবা r ও p হতে প্রতিপাদিত কৌণিক ভরবেগের ন্যায় রাশিসমূহকে ব্যবহার করা যেতে পারে।
কখনো কখনো সমীকরণসমূহ রৈখিক এবং প্রায়ই নির্ভুলভাবে সমাধানযোগ্য হয়। সাধারণত, সমীকরণসমূহ অরৈখিক এবং নির্ভুলভাবে সমাধানের অযোগ্য হয়ে থাকে, তাই সমীকরণের সমাধানের জন্য অবশ্যই বিভিন্ন আসন্ন মান ব্যবহার করা হয়। অরৈখিক সমীকরণসমূহের সমাধান বিশৃঙ্খল আচরণ দেখাতে পারে যা প্রাথমিক শর্তসমূহের প্রতি ব্যবস্থাটির সংবেদনশীলতার উপর নির্ভরশীল।
ইতিহাস[সম্পাদনা]
ঐতিহাসিকভাবে, চিরায়ত বলবিদ্যায় ভারী বস্তুর গতির ব্যাখ্যায় গতির সমীকরণসমূহ প্রথম দৃষ্টিগোচর হয়, যার উল্লেখযোগ্য প্রয়োগ ঘটেছে খ-বস্তু বলবিদ্যায় গ্রহসমূহের অবিরাম আবর্তন গতির অনুমানের ক্ষেত্রে, যেমন: নেপচুন গ্রহ আবিষ্কৃত হওয়ার আগেই গাণিতিক অনুমিতির দ্বারা এর উপস্থিতির পূর্বাভাস পাওয়া গিয়েছিল। এছাড়া সৌর জগতের স্থিতিশীলতা[৩] পর্যবেক্ষণেও গতির সমীকরণসমূহের উল্লেখ পাওয়া যায়।
সৃতিবিদ্যা ও গতিবিদ্যার সংশ্লিষ্ট এবং তিন সহস্রাব্দের অধিক সময় ধরে দ্বিধাদ্বন্দে থাকা, বেড়ে ওঠা বা অভ্যুত্থান ও স্বতঃসংশোধন— এসব ক্ষুদ্র ক্ষুদ্র পদক্ষেপের মাধ্যমে বিকশিত হওয়া মহাবিশ্বের গাণিতিক মডেলসমূহের সাথে সম্পর্কযুক্ত এবং পরিচিত নামদের ও ইতিহাসের পাতা থেকে ম্লান হয়ে যাওয়াদের অবদানের অন্তর্ভুক্ত বৃহৎ বৃহৎ আকারের কাজগুলো পর্যবেক্ষণ করা অতীব গুরুত্বপূর্ণ।
পুরাকাল থেকেই যাজক, জ্যোতিষী এবং জ্যোতির্বিদরা সূর্যগ্রহণ, চন্দ্রগ্রহণ, অয়নান্ত বৃত্তে সূর্যের অবস্থান তথা কর্কটক্রান্তি ও মকরক্রান্তি দিবস, নিরক্ষরেখায় সূর্যের অবস্থান তথা মহাবিষুব ও জলবিষুব এবং চাঁদের পর্যায়কালের সফল পূর্বাভাস বা ভবিষ্যদ্বাণী করলেও আদতে সেগুলো ছিল গাণিতিক প্রক্রিয়াদির এক সমন্বয় (algorithm) এবং তাদের কাজে সাহায্যের জন্য তখন এতদ্ভিন্ন আর কিছুই ছিল না। প্রাচীন গ্রিকবাসী ও রোমান নিরীক্ষাবিদদের দ্বারা জ্যামিতির উন্নতির ফলে বৃহৎ প্রগতি সত্ত্বেও গতির প্রথম সূত্রটির আবির্ভাবের পূর্বে আমাদের আরেকটি সহস্রাব্দ অপেক্ষা করতে হয়েছিল।
ইউরোপে গ্রিক, ভারতীয় ও ইসলামিক পণ্ডিতদের জ্ঞানবিজ্ঞানের (যেমন: ইউক্লিডের এলিমেন্টস, আর্কিমিডিসের কাজ ও আল খোয়ারিজমির গ্রন্থাদি) উন্মোচন-উদ্ঘাটন মুসলিমদের দ্বারা স্পেনে শুরু হয়, এবং এ সময় গোটা ইউরোপ থেকে শিক্ষার্থী ও পণ্ডিতেরা স্পেনে আসতে থাকে; তারা সেখানে অধ্যয়ন, প্রতিলিপন আর অধীত বিদ্যার ল্যাটিনে অনুবাদ করে। ইউরোপে আরবীয় তথা ভারতীয় সংখ্যা পদ্ধতির উন্মেষের ফলে এবং গণনাকার্যে এর স্বাচ্ছন্দ্য ও সহজবোধ্যতার কারণে প্রথমত পণ্ডিতেরা এবং পরে ব্যবসায়ীরা সে সব শিখতে উদ্বুদ্ধ হয়। এছাড়াও গণনাকার্যে এই স্বাচ্ছন্দ্যবোধ সারা ইউরোপে জ্ঞানের বিস্তার ঘটাতে অনুপ্রেরণা যোগায়। (দেখুন গণিতের ইতিহাস)
১৩শ শতাব্দীর মধ্যেই অক্সফোর্ড[৪] ও প্যারিসের বিশ্ববিদ্যালয়গুলো [৫] চালু হয়। বিদ্যার্থীরা তখন গণিত ও দর্শন নিয়ে পড়ার পাশাপাশি পার্থিব জীবনের নিত্যনৈমিত্তিক টুকিটাকি ঘটনাবলী নিয়েও কিছুটা উদ্বিগ্ন উৎকণ্ঠিত ছিল, তাদের ভাবনার মধ্যে খ-বস্তর গতিও ছিল; তবে তাদের চিন্তাভাবনার ক্ষেত্রগুলি আধুনিক সময়ের মতো এতো স্পষ্টভাবে চিহ্নিত ছিলনা এটা উল্লেখ করতেই হবে। এমন সময়েই একাধারে গণিতবিদ জ্যোতির্বিদ জ্যোতিষী ও চিকিৎসাবিদ জোহানেস ক্যাম্পানাস ইউক্লিড ও অ্যারিস্টটলের কাজের বহু সংখ্যক সম্পাদনা ও সারাংশ (redactions and compendia) রচনা করেন যেগুলো ছাত্রদের কাছে শুধু সহজবোধ্যই ছিল না বরং সেগুলো ছাত্রদেরকে আরও কিছু প্রশ্নের বিশেষকরে এরিস্টটলের রেখে যাওয়া দার্শনিক সমস্যাগুলোর সম্মুখীন করেছিল। ক্যাম্পানাসের এসব রচনাই ছাত্রদেরকে গতিশীল বস্তুর রাশিসমূহের পারস্পারিক সম্পর্কের বহিঃপ্রকাশরূপে অ্যারিস্টটলের অসীমতা ও ইউক্লিডের অনুপাত তত্ত্বের ধারণারসমূহের সাথে পরিচয় করিয়ে দেয়। অ্যারিস্টটল সংখ্যার প্রতি খুবই দুর্বল ছিলেন, তিনি সব কিছুই সংখ্যার মাধ্যমে প্রকাশ করার চেষ্টা করেছিলেন। এই সম্পর্কগুলো পরে সূত্রের রূপ পায় এবং এই অধ্যয়ন-অনুসন্ধানই জ্ঞানের নতুন এক শাখার পথ দেখায় যা এখন পদার্থবিজ্ঞান নামে পরিচিত।[৬]
প্যারিস বিশ্ববিদ্যালয়ের বুদ্ধিজীবিদের মর্যাদার অনুকরণে অক্সফোর্ড বিশ্ববিদ্যালয়ের মের্টন কলেজও প্রাকৃতিক বিজ্ঞানের অনুরাগী (মূলত পদার্থবিজ্ঞান, জ্যোতির্বিজ্ঞান ও গণিতের) একদল স্কলারের মাথার উপর ছাতা মেলে ধরে। এই পণ্ডিতদের মধ্যে থমাস ব্র্যাডওয়ার্ডাইন অ্যারিস্টটলের রাশিসমূহের (যেমনঃ দূরত্ব ও বেগ) প্রসারণ ঘটিয়ে এগুলোকে তীক্ষ্ণ ও বিবর্ধিত করে তোলেন। ব্র্যাডওয়ার্ডাইন বল, প্রতিরোধ, সময়, দূরত্ব ও বেগের সমন্বয়ে একটি সূচকীয় সূত্রের প্রস্তাব করেন। নিকোল অরেস্মে ব্র্যাডওয়ার্ডাইনের সিদ্ধান্তের আরও প্রসার ঘটান। মের্টন স্কুল প্রমাণ করে যে, একটি সুষমভাবে ত্বরিত গতির (uniformly accelerated motion) অধীনে চলমান বস্তুর গতির রাশি (quantity of motion), ত্বরিত গতির মাধ্যমে অর্ধ-পথ অতিক্রমের পর লব্ধ দ্রুতিতে একটি সুষম গতীয় রাশির (quantity of a uniform motion) অনুরূপ বা সমান।
গ্যালিলিওর পূর্বে ক্ষুদ্র সময় ব্যবধান পরিমাপ করা যেত না, ফলে সময় ও গতির ঘনিষ্ট সম্পর্ক সৃতিবিদ্যার লেখকদের জন্য দুর্বোধ্যই ছিল। তারা সময়কে দূরত্বের ফাংশন হিসেবে এবং মুক্তভাবে পড়ন্ত বস্তুর ক্ষেত্রে বৃহত্তর বেগকে (greater velocity), বৃহত্তর সীমা বা উচ্চতার (greater elevation) ফলাফল হিসেবে ব্যবহার করতেন। স্পেনিশ ধর্মতত্ত্ববিদ ডোমিংগো দে সোটো অ্যারিস্টটলীয় পদার্থবিজ্ঞানের উপর লেখা তার এক ভাষ্যে (১৫৪৫ এ প্রকাশিত) "uniform difform" গতির সংজ্ঞা নির্ধারণ করেন যা আসলে সুষমভাবে ত্বরিত গতি (uniformly accelerated motion) এবং শুধু তিনিই এই ভাষ্যে বেগ শব্দটিকে সময়ের সমানুপাতিক হিসেবে না ব্যবহার করে ঘোষণা করেন যে, মুক্তভাবে পড়ন্ত বস্তুর গতি ও প্রাসের গতি নির্ভুলভাবে শনাক্তযোগ্য; তবে সময়, বেগ ও দূরত্বনির্ভর কোন সূত্রের প্রস্তাব, ইঙ্গিত বা প্রমাণ কোনটিই তিনি দেন নি। ডোমিংগো দে সোটোর ভাষ্য ত্বরণের সংজ্ঞা এবং তার পর্যবেক্ষণের সাথে মারাত্মকভাবে মিলে যায় ও সঠিক প্রমাণিত হয়। ত্বরণকে তিনি সময়ের সাথে গতির (বেগ) পরিবর্তনরূপে দেখেছিলেন এবং ঊর্ধমুখী গতির ক্ষেত্রে ত্বরণ যে ঋণাত্মক হবে সেটাও পর্যবেক্ষণ করেছিলেন।
এই ধরনের টীকা-ভাষ্য-বক্তব্য সারা ইউরোপে ছড়িয়ে পড়লে স্পষ্টতই তা গ্যালিলিও ও অন্যদেরকে প্রভাবিত করে এবং সৃতিবিদ্যার ভিত্তি স্থাপনে সহায়ক হয়ে উঠে।[৭] গ্যালিলিও তার অনুসন্ধান কার্যে গড় দ্রুতি উপপাদ্য তথা মের্টন নিয়ম ব্যবহার করে জ্যামিতিকভাবে s = +১/২gt2 সমীকরণে উপনীত হন[৮], যা এখন সৃতিবিদ্যার সমীকরণসমূহের মধ্যে এক বিশেষ ঘটনা হিসেবে পরিচিত। বর্তমান সময়ের সুপরিচিত গাণিতিক যুক্তির প্রয়োগ তিনি করতে পারেন নাই। দ্রুতি, দূরত্ব, সময় ও ত্বরণের মধ্যে সম্পর্ক তখনকার সময়ে জানা ছিল না।
গ্যালিলিও'ই প্রথম দেখান যে প্রাসের গতি অধিবৃত্তাকার। কেন্দ্রবিমুখী বল সম্পর্কে গ্যালিলিওর জানা ছিল, তিনি ভরবেগের একটি সঠিক সংজ্ঞা দেন। ভরবেগকে গতিবিদ্যার মৌলিক রাশি হিসেবে তুলে ধরার এই ঝোঁক-প্রবণতা খুবই তাৎপর্যপূর্ণ। বেগ ও ওজনের গুণফলের মাধ্যমে তিনি ভরবেগ পরিমাপ করেন; ভরের ধারণা তখনও অজানা যা পরে আসে এবং হাইগেন্স ও নিউটন এর উন্নয়ন করেন। সরল দোলকের দোলনের ক্ষেত্রে গ্যালিলও তার ডিসকোর্সে বলেন[৯] "একটি চাপ বরাবর (দোলকের ববের) অবরোহণের ফলে লব্ধ প্রতিটি ভরবেগ, একই চাপ বরাবর গতিশীল একই বস্তুর আরোহণের জন্য যা দায়ী তার সমান"। তিনি গতির প্রথম ও দ্বিতীয় সূত্র যে আয়ত্তে নিয়ে এসেছিলেন প্রাস নিয়ে তার বিশ্লেষণী কাজ সে ইঙ্গিতই দেয়। তবে বস্তু কিংবা পৃথিবীর অভিকর্ষ কোনটির জন্যই তিনি এগুলোকে সরলীকরণ ও প্রয়োগযোগ্য করে তুলেন নি, এ অবদান নিউটনের।
স্থির বস্তুর ক্ষেত্রে "জড়তা" শব্দটির ব্যবহার কেপলারের মাধ্যমে শুরু হয়। এখন গতির প্রথম সূত্রটিকে প্রায়শই জড়তার সূত্র বলা হয়।
গ্যালিলিও অ্যারিস্টটলের কিছু ভুল সংশোধন করলেও তিনি ক্রিয়া-প্রতিক্রিয়ার সমতার সূত্র তথা গতির তৃতীয় সূত্রটি পুরোপুরি আয়ত্ত করতে পারেন নি। এছাড়াও সাইমন স্টিভেন ও অন্যান্যদের সাথে তিনিও স্থিতিবিদ্যার বই লেখেন। তিনি বলের সামান্তরিক সূত্রটি প্রণয়ন করলেও তিনি এর তাৎপর্যটি পুরোপুরি বুঝতে পারেন নি।
এছাড়াও গ্যালিলিও দোলকের সূত্র নিয়েও আগ্রহী ছিলেন। দোলকের প্রথম সূত্রটি তিনি তরুণ থাকাকালীন সময়েই পর্যবেক্ষণ করেন। ১৫৮৩ সালে পিসার ক্যাথেড্রালে প্রার্থনা করার সময় একটি বিশালাকৃতির দীপের প্রতি তার নজর আটকে যায়। দীপটি আলো ছড়াচ্ছিল আর দুলছিল। তিনি তার নাড়ির স্পন্দনের সাথে সময় মিলিয়ে এর পর্যায়কাল পর্যবেক্ষণ করেন। দোলকের সমকালীনত্ব (isochronism) উদ্ঘাটনের মাধ্যমে তিনি লক্ষ্য করেন যে বাতিটির দোলনের পর্যায় বরাবর একই, এমনকি দোলন অনেকাংশে হ্রাস পাওয়ার পরেও সেটা তার কাছে একই মনে হয়েছিল।
পরে তিনি আরও সতর্ক পরীক্ষা-নিরীক্ষা চালান যা তিনি তার ডিসকোর্সে বর্ণনা করেন এবং লেখেন, দোলনের পর্যায়কাল দোলকের দৈর্ঘ্যের বর্গমূলের উপর নির্ভর করে তবে দোলকের (ববের) উপর এটি নির্ভর করে না অর্থাৎ ভরের ব্যাপারে এটি স্বাধীন।
এভাবেই আমরা র্যনে দেকার্ত, নিউটন, লিবনিজ এবং অন্যান্যদের কাছে পৌঁছাই আর উপনিত হই গতির সমীকরণগুলোর বিবর্তিত গঠনসমূহের মাঝে যা এখন স্বীকৃত হচ্ছে আধুনিক হিসেবে।
এছাড়াও পরে তড়িৎ ক্ষেত্র ও চৌম্বক ক্ষেত্রে চার্জিত কণার গতি ব্যাখ্যায় তড়িৎ গতিবিদ্যাতেও গতির সমীকরণসমূহের প্রয়োগ দেখা যায়। লরেঞ্জ বল হল সাধারণ সমীকরণ যা, তড়িৎ ক্ষেত্র ও চৌম্বক ক্ষেত্র বলতে কী বোঝায় তার সংজ্ঞা হিসেবে ব্যবহৃত হয়। বিশেষ আপেক্ষিকতা ও সাধারণ আপেক্ষিকতা তত্ত্বের আবির্ভুত হওয়ার সাথে সাথে স্থান-কাল নামক তাত্ত্বিক ধারণাটির আবির্ভাব হয়, ফলত আলোর সসীম বেগের এবং স্থান-কালের বক্রতার জন্য গতির চিরায়ত সমীকরণগুলিও মোডিফাই করা হয়। বলের রূপান্তর অথবা শক্তির রূপান্তর দ্বারা প্রভাবিত হয়ে উক্ত সকল ক্ষেত্রেই, অবস্থান-স্থানাঙ্ক ও সময়-স্থানাঙ্কের অধীনে কণার গতিপথ (trajectory) ব্যাখ্যায় ব্যবকলনী সমীকরণকে একটি ফাংশন হিসেবে বয়বহার করা হয়।[১০]
যাইহোক, কোয়ান্টাম বলবিদ্যার সমীকরণগুলো, কণার স্পেস ও সময় স্থানাঙ্কের মাধ্যমে কোয়ান্টাম স্টেটের আচরণ ব্যাখ্যাকারী তরঙ্গফাংশনের ব্যবকলনী সমীকরণ হওয়ায়, কোয়ান্টাম বলবিদ্যার এই সমীকরণগুলোকেও "গতির সমীকরণ" হিসেবে বিবেচনা করা যেতে পারে। পদার্থবিজ্ঞানের অন্যান্য ক্ষেত্রগুলোতেও গতির সমীকরণের অনুরূপ বিষয়-বস্তু রয়েছে, যেগুলো তরঙ্গ, প্রবাহী অথবা ক্ষেত্র ইত্যাদি ভৌত প্রপঞ্চ (ফেনোমেনা) হিসেবে স্বীকৃত।
একটি কণার জন্য সৃতিবিদ্যার সমীকরণ[সম্পাদনা]
সৃতিবিদ্যার রাশিসমূহ[সম্পাদনা]

অতি ক্ষুদ্র সময় ব্যবধানকে তাৎক্ষণিক সময় বলে। t তাৎক্ষণিক সময়ে কোন কণার তাৎক্ষণিক অবস্থান r = r(t), তাৎক্ষণিক বেগ v = v(t), ত্বরণ a = a(t) এর সাধারণ ও স্থানাঙ্ক-অনির্ভর সংজ্ঞা রয়েছে।[১১] সংজ্ঞানুসারে পাই—
লক্ষ্যণীয় যে, বেগের অভিমুখ সর্বদা কণার গতির দিকে, অন্য কথায় বক্রপথ হল স্পর্শক ভেক্টর। সহজভাবে বলা যায়, প্রথম ডেরিভেটিভ বা অন্তরজ বক্ররেখার স্পর্শকের সাথে সম্পর্কিত। তবে বক্রপথের ক্ষেত্রে, ত্বরণের দিক হবে বক্রতার কেন্দ্রের দিকে। আরও সহজভাবে বলা যায়, দ্বিতীয় ডেরিভেটিভ বক্রতার সাথে সম্পর্কিত।
কোন বস্তু একটি স্থির বিন্দু বা অক্ষের সাপেক্ষে ঘুরতে থাকলে এর গতিকে ঘূর্ণন গতি বলে। ঘূর্ণন গতির ক্ষেত্রে রৈখিক গতির সদৃশ রাশিগুলো হবে কৌণিক ভেক্টর θ = θ(t) (বিন্দু বা অক্ষের সাপেক্ষে বস্তু যে কৌণিক দূরত্ব অতিক্রম করে), কৌণিক বেগ ω = ω(t) এবং কৌণিক ত্বরণ α = α(t)। তাহলে কৌণিক গতির সংজ্ঞা হতে পাই—
এখানে n̂ একটি একক ভেক্টর যার দিক ঘূর্ণন অক্ষের দিকে এবং θ হল অক্ষের সাপেক্ষে বস্তুর ঘূর্ণন কোণ বা অতিক্রান্ত কৌণিক দূরত্ব।
এবার একটি বিন্দু কণা বিবেচনা করা যাক যা প্রসঙ্গ কাঠামোর একটি অক্ষের সাপেক্ষে ω কৌণিক বেগে আবর্তন করছে। এর অবস্থান ভেক্টর r (ঘূর্ণন অক্ষ থেকে কণার ভ্রমণ পথের ব্যাসার্ধ) এবং স্পর্শীয় বেগ v। তাহলে আমরা যে সমীকরণটি পাব[১২] —
এই সমীকরণটি আবর্তনশীল কণার কৌণিক বেগ ও রৈখিক বেগের মধ্যে সম্পর্ক নির্দেশ করে। ঘূর্ণায়মান দৃঢ় বস্তুর অভ্যন্তরে প্রতিটি বিন্দুতে এই সম্পর্কগুলো বিদ্যমান।
সম ত্বরণ বা সুষম ত্বরণ[সম্পাদনা]
সরল রেখা বরাবর ধ্রুব বা সম ত্বরণে চলমান কোন কণার গতির ব্যবকলনী সমীকরণটি একটি সাধারণ সমীকরণ। ত্বরণ যেহেতু ধ্রুবক তাই বস্তকণার অবস্থানের দ্বিতীয় ডেরিভেটিভটিও ধ্রুবক। ত্বরণজাত ফলাফল নিচে সংক্ষিপ্ত আকারে উত্থাপন করা হল।
সরল রেখা বরাবর ধ্রুব অনুবাদী ত্বরণ[সম্পাদনা]
পদার্থবিজ্ঞানে অনুবাদ বলতে ঘূর্ণন ছাড়াই সুষম গতিকে বোঝায়। একটি সরল রেখা বরাবর ধ্রুব ত্বরণে গতিশীল কণার উপর ত্রিমাত্রিকভাবে রৈখিকহারে এই সমীকরণগুলো প্রযুক্ত হয়। অবস্থান, বেগ ও ত্বরণ ভেক্টরত্রয় সমরৈখিক হওয়ায় অর্থাৎ এরা পরস্পরের সমান্তরালে বা একই রেখা বরাবর ক্রিয়া করায় এদের শুধু মান প্রয়োজন এবং বেগ ভেক্টরটি সরল রেখা বরাবর ক্রিয়া করায় গতীয় সমস্যাটি ত্রিমাত্রিক থেকে একমাত্রিক বা রৈখিকে রূপান্তরিত হয়। এক্ষেত্রে গতির সমীকরণসমূহ হবে—
যেখানে:—
- কণার আদি অবস্থান = r0
- কণার শেষ অবস্থান = r
- কণার আদি বেগ = v0
- কণার শেষ বেগ = v
- কণার ত্বরণ = a
- সময় ব্যবধান = t
r(t0) = r0 এবং v(t0) = v0 আদি শর্তে বেগ ও ত্বরণের সংজ্ঞাকে সমাকলন করলে যথাক্রমে নং ও নং সমীকরণ পাওয়া যাবে—
স্কেলার করে পাই—
নং সমীকরণ গড় বেগ +v + v০/২ এর সাথে জড়িত। সুষম ত্বরণের ক্ষেত্রে বেগ স্বতঃস্ফূর্তভাবে রৈখিকহারে বৃদ্ধি পায়। সুতরাং গড় বেগকে সময় দ্বারা গুণ করলে, বেগ v0 হতে v এ বৃদ্ধিকালে কণা যে দূরত্ব অতিক্রম করে তা পাওয়া যাবে। বর্গাকার লেখচিত্রে বেগ বনাম সময় লেখ অঙ্কন করেও এ দূরত্ব বের করা যাবে। বীজগাণিতিকভাবে (i) নং সমীকরণ হতে এই সমীকরণটি প্রতিপাদন করা যায়। (i) নং সমীকরণ হতে আমরা পাই—
একে নং সমীকরণে প্রতিস্থাপন করে পাই—
এর সাধারণ আকার হবে—
স্কেলার আকার হবে—
নং সমীকরণ থেকে পাই—
নং-এ t প্রতিস্থাপন করে পাই—
পুনরায় নং সমীকরণ থেকে—
কে নং বসাই—
মূলত প্রথম চারটি সমীকরণ প্রয়োজনীয়, পঞ্চমটি ঐচ্ছিক।
এখানে a হল ধ্রুব ত্বরণ। যেমন: অভিকর্ষের প্রভাবে মুক্তভাবে পড়ন্ত বস্তুর ত্বরণ তথা অভিকর্ষজ ত্বরণ হল ধ্রুব ত্বরণ। অভিকর্ষের প্রভাবে গতিশীল বস্তুর ক্ষেত্রে আদর্শ অভিকর্ষ g পদটি ব্যবহৃত হয়। অভিকর্ষের দরুন আদর্শ ত্বরণকে অর্থাৎ মুক্তভাবে পতনজনিত আদর্শ ত্বরণকে আদর্শ অভিকর্ষ বলা হয়। লক্ষ্যণীয় যে, সমীকরণগুলোর প্রতিটিতে চারটি চলক বিদ্যমান। সুতরাং সরণ, আদি বেগ, শেষ বেগ, ত্বরণ ও সময় এই পাঁচটি চলকের দুটি দেওয়া থাকলে অন্য তিনটি অনায়াসেই বের করা যাবে।
অপেক্ষাকৃত নিচের ক্লাশের শিক্ষার্থীদের জন্য এই একই সমীকরণগুলোই ভিন্ন কয়েকটি প্রতীকের মাধ্যমে লেখা হয়। যেমন:
এখানে v0 এর পরিবর্তে u এবং r - r0 এর পরিবর্তে s ব্যবহৃত হয়েছে। এই সমীকরণগুলোকে SUVAT সমীকরণ বলা হয়, যেখানে: s = সরণ, u = আদি বেগ, v = শেষ বেগ, a = ত্বরণ এবং t = সময়।[১৩][১৪]
যে কোন দিকে ধ্রুব রৈখিক ত্বরণ[সম্পাদনা]

আদি অবস্থান, আদি বেগ ও আদি ত্বরণ ভেক্টরত্রয়ের সমরৈখিক হওয়া বাধ্যতামূলক নয় এবং এদের প্রায় অভিন্ন আকার বিদ্যমান। একমাত্র পার্থক্য এই যে, বেগের বর্গ মানের জন্য ডট বা স্কেলার গুণন প্রয়োজন। ব্যবকলনী প্রক্রিয়াগুলো অপরিহার্যভাবেই সমরৈখিকের ঘটনার মতই। এক্ষেত্রে সমীকরণ আকার হবে—
যদিও টরিসেলির সমীকরণটি (() নং সমীকরণ) ডট গুণনের বণ্টনের সূত্রের দ্বারা নিম্নরূপে প্রতিপাদন করা যায়:—
প্রয়োগ[সম্পাদনা]
সৃতিবিদ্যার সাধারণ এবং বহুল আলোচিত সমস্যাবলী যেমন: প্রাসের গতি, উদাহরণ স্বরূপ একটি বলকে u আদিবেগে উপরের দিকে বায়ুতে নিক্ষেপ করলে বলটির নিম্নমুখী গতি শুরুর পূর্বে এটি সর্বোচ্চ কত উচ্চতায় উঠবে গতির এই সমীকরণ ব্যবহার করে যে কারও পক্ষে তা নির্ণয় করা সম্ভব। বলটি নিচে নামার সময় এর ত্বরণটি হবে স্থানীয় ত্বরণ অর্থাৎ অভিকর্ষজ ত্বরণ g। এখানে অবশ্যই খেয়াল রাখতে হবে যে, ব্যবহৃত রাশিসমূহ স্কেলার হলে সরণ, বেগ ও ত্বরণের অভিমুখ খুবই তাৎপর্যপূর্ণ এক বিষয়। আদতে এরা একমুখী ভেক্টর হতে পারে। বলটির সর্বোচ্চ উচ্চতা s নির্ণয়ের জন্য একে ভূমি থেকে উপরের দিকে বিবেচনা করলে ত্বরণ a অবশ্যই -g হবে, যেহেতু অভিকর্ষজ বল নিচের দিকে ক্রিয়া করে এবং এই কারণে বলটির উপর প্রযুক্ত ত্বরণও -g হবে।
এখন, নং সমীকরণ হতে পাই—
সর্বোচ্চ বিন্দতে বলটি স্থির, ফলে সেখানে v = 0,
- v = 0 প্রতিস্থাপন করে এবং ঋণাত্মক মান বর্জন করে পাই—
সর্বোচ্চ উচ্চতা,
এছাড়াও এই সমীকরণগুলো প্রতিপাদন করে ভূমির সাথে তির্যকভাবে নিক্ষিপ্ত বস্তুর সঞ্চারপথ, সর্বোচ্চ পাল্লা এবং সঞ্চারপথের যেকোন বিন্দুতে বস্তুর অবস্থান কালের সময়ের সূত্রও বের করা যাবে।
ধ্রুব বৃত্তীয় ত্বরণ[সম্পাদনা]
উপরের সমীকরণগুলোর অনুকরণে ঘূর্ণন গতির জন্য অক্ষীয় ভেক্টর নির্ভর সমীকরগুলোকে নিম্নোক্তভাবে লেখা যায়। উল্লেখ্য যে, অক্ষীয় তথা ঘূর্ণন ভেক্টরগুলো অবশ্যই ঘূর্ণন অক্ষের সমান্তরাল হবে এবং এক্ষেত্রে ভেক্টরের শুধু মান প্রয়োজন।
যেখানে, α = ধ্রুব কৌণিক ত্বরণ, ω = ধ্রুব কৌণিক বেগ, ω0 = আদি কৌণিক বেগ, θ = কৌণিক সরণ বা ঘূর্ণন কোণ, θ0 = আদি কোণ এবং t = সময় ব্যবধান= কণার θ0 থেকে θ অবস্থানে যেতে প্রয়োজনীয় সময়।
সাধারণ সমতলীয় গতি[সম্পাদনা]
এগুলো কোন সমতলে সঞ্চারপথকে আড়াআড়িভাবে অতিক্রমকারী কণার কাইনেমেটিক সমীকরণ যাদেরকে r = r(t) অবস্থান দ্বারা বর্ণনা করা হয়[১৫]। কৌণিক বেগ ω এবং কৌণিক ত্বরণ α এর জন্য ভৌত রাশির সংজ্ঞার ভিত্তিতে এই সমীকরণগুলো সাধারণভাবে কোন সমতলীয় মেরু স্থানাঙ্কে অবস্থান ভেক্টরের সময় ডেরিভেটিভ। এগুলো সময়ের সাথে পরিবর্তনশীল তাৎক্ষণিক রাশি।
কণার অবস্থান:
যেখানে êr এবং êθ হচ্ছ মেরূ একক ভেক্টর। একে সময়ের সাপেক্ষে ব্যবকলন করলে বেগ পাওয়া যাবে।
এখানে +dr/dt এবং rω হল ঘূর্ণনের ফলে সৃষ্ট যথাক্রমে রেডিয়াল উপাদান এবং অতিরিক্ত উপাদান।
একে পুনরায় সময়ের সাপেক্ষে ব্যবকলন করলে ত্বরণ পাওয়া যাবে।
এখানে ত্বরণ রেডিয়াল ত্বরণ +d২r/dt২, কেন্দ্রমুখী ত্বরণ –rω2, কোরিওলিস ত্বরণ 2ω+dr/dt এবং কৌণিক ত্বরণ rα এ বিভাজিত।
এই সমীকরণগুলোর মাধ্যমে ব্যাখ্যাযোগ্য গতির বিশেষ অবস্থাসমূহকে নিচের ছকে সংক্ষেপে উত্থাপন করা হয়েছে। রেডিয়াল উপাদান বা কৌণিক উপাদানগুলির যে কোন একটি শুন্য হবে এবং গতির অশূন্য উপাদান সুষম ত্বরণকে ব্যাখ্যা করে এমন ক্ষেত্রে দুটি বিশেষ অবস্থা আগেই আলোচনা করা হয়েছে।
| গতির অবস্থা | ধ্রুবক r | t-তে রৈখিক r | t-তে দ্বিঘাতী r | t-তে অরৈখিক r |
|---|---|---|---|---|
| ধ্রুবক θ | নিশ্চল | সুষম অনুবাদ (ধ্রুব অনুবাদী বেগ) | ধ্রুব অনুবাদী ত্বরণ | অনিয়মিত অনুবাদ |
| t-তে রৈখিক θ | বৃত্তীয়পথে সুষম কৌণিক গতি (ধ্রুব কৌণিক বেগ) | সর্পিলপথে সুষম কৌণিক গতি, ধ্রুব রেডিয়াল বেগ | সর্পিলপথে কৌণিক গতি, ধ্রুব রেডিয়াল ত্বরণ | সর্পিলপথে সুষম কৌণিক গতি, পরিবর্তনশীল রেডিয়াল ত্বরণ |
| t-তে দ্বিঘাতী θ | বৃত্তীয়পথে সুষম কৌণিক ত্বরণ | সর্পিলপথে সুষম কৌণিক ত্বরণ, ধ্রুব রেডিয়াল বেগ | সর্পিলপথে সুষম কৌণিক ত্বরণ, ধ্রুব রেডিয়াল ত্বরণ | সর্পিলপথে সুষম কৌণিক ত্বরণ, পরিবর্তনশীল রেডিয়াল ত্বরণ |
| t-তে অ-রৈখিক θ | বত্তপথে অনিয়মিত কৌণিক ত্বরণ | সর্পিলপথে অনিয়মিত কৌণিক ত্বরণ, ধ্রুব রেডিয়াল বেগ | সর্পিলপথে অনিয়মিত কৌণিক ত্বরণ, ধ্রুব রেডিয়াল ত্বরণ | সর্পিলপথে অনিয়মিত কৌণিক ত্বরণ, পরিবর্তনশীল রেডিয়াল ত্বরণ |
সাধারণ ত্রিমাত্রিক গতি[সম্পাদনা]
ত্রিমাত্রিক স্থানে (r, θ, φ) গোলকীয় স্থানাঙ্কে êr, êθ এবং êφ একক ভেক্টরত্রয়ের সংশ্লিষ্ট অবস্থান, বেগ এবং ত্বরণ যথাক্রমে—
ধ্রুব φ এর ক্ষেত্রে এটা উপরের সমতলীয় সমীকরণসমূহে সংকুচিত হয়।
গতিশীল বস্তুর গতিবিদ্যার সমীকরণ[সম্পাদনা]
নিউটনীয় বলবিদ্যা[সম্পাদনা]
নিউটনের দ্বিতীয় গতিসূত্রটি দিয়ে গতির প্রথম সাধারণ সূত্রটির উন্নয়ন ঘটানো হয়েছে। নিউটনের দ্বিতীয় গতিসূত্রটিকে ভরবেগের পরিবর্তনের সূত্রও বলা হয়। নিউটনের দ্বিতীয় গতিসূত্রটি হল, গতিশীল বস্তুর ভরবেগের পরিবর্তনের হার এর উপর প্রযুক্ত বলের সমানুপাতিক এবং বল যে দিকে ক্রিয়া করে ভরবেগের পরিবর্তনও সেদিকে হবে।
- ধরা যাক, বস্তুর ভরবেগ, p = p(t) = mv(t) এবং বল, F = F(x(t), v(t), t);
তাহলে বলের সমীকরণটি হবে [১৬]
- (সমানুপাতিক ধ্রুবককে ধরা হয়েছে)।
এটি নিউটনের দ্বিতীয় গতিসূত্রটির অতি সাধারণ রূপ যা ভরবেগের পরিবর্তনের হার নির্দেশ করে। উল্লেখ্য যে, এখানে F হল বস্তুটির উপর প্রযুক্ত বল, আলোচনাধীন বস্তুটি দ্বারা অন্য বস্তুর উপর প্রযুক্ত বল নহে।
- এছাড়াও সমীকরণের ভরবেগকে ভর ও বেগের গুণন দ্বারা প্রতিস্থাপন করে নিম্নরূপেও লেখা যায়—
- (যেহেতু ভর m নিউটনীয় বলবিদ্যায় ধ্রুব)
সূত্রের এই রূপটি অধিক জনপ্রিয়।
নিউটনের দ্বিতীয সূত্রটি বিন্দুতে কাজ করে, যেমন কোন কণা এবং দৃঢ় বস্তুর অভ্যন্তরে যে কোন বিন্দু। এছাড়াও ভর সমষ্টি যেমন: আকারহীন কঠিন বা প্রবাহীর ক্ষেত্রেও এটি কাজ করে। প্রতিটি ক্ষেত্রেই গতি হিসেবে সিস্টেমের গতি বিবেচনা করা হয়। আরও জানতে Material derivative বা জড় অন্তরজ দেখুন। এক্ষেত্রে ভর ধ্রুবক নয়, ভর ও বেগের সময় ডেরিভেটিভের জন্য Product rule বা গুণের সূত্র ব্যবহার পর্যাপ্ত নয়। এবং নিউটনের দ্বিতীয় গতিসূত্রটির জন্য ভরবেগের সংরক্ষণের সাথে সঙ্গতিপূর্ণ কিছু পরিবর্তন প্রয়োজন। দেখুন Variable-mass System বা পরিবর্তনযোগ্য-ভর ব্যবস্থা।
নিউটনের সূত্র ব্যবহার করে গতিসূত্রগুলোকে সহজে ভেক্টর আকারে লেখা যায় কিন্তু এর ফলে সমীকরণের অংশবিশেষে স্থানিক স্থানাঙ্ক ও সময়জনিত জটিলতা তৈরি হতে পারে যেগুলো সমাধান করা সহজ নয়। এসব সমস্যার পূর্ণাঙ্গ সমাধানের ক্ষেত্রে প্রায়ই বাড়তি চলকের আবির্ভাব ঘটে। তাই সকল সিস্টেমের গতি নির্ণয়ের ক্ষেত্রে নিউটনের সূত্রগুলো সবসময় সর্বাধিক কার্যকর পদ্ধতি নয়। কার্তেসীয় স্থানাংকে আয়তাকার জ্যামিতির সাধারণ সমস্যাগুলোতে নিউটনের সূত্রগুলো সুন্দরভাবে কাজ করলেও অন্যান্য স্থানাঙ্ক ব্যবস্থায় তা নাটকীয়ভাবে জটিল হয়ে পড়ে।
অধিক জটিল সিস্টেমের ক্ষেত্রে ভরবেগের সাধারণীকরণ করা হয়েছে এবং এটি বিশেষ ও সাধারণ আপেক্ষিকতাকে সাধারণীকরণ করে। একারণে ভরবেগ আকারটির ব্যবহার অধিক সুবিধাজনক। ( দেখুন: four-momentum বা চার-ভরবেগ)[১৬]। এছাড়াও ভরবেগের সংরক্ষণও ব্যবহার করা যেতে পারে। যাই হোক, কোন বস্তুর উপর ক্রিয়াশীল লব্ধি বল ভরবেগকে প্রকাশ করে, নিউটনের সূত্রগুলো এই সত্যতার সাথে খুবই সঙ্গতিপূর্ণ হওয়ায় নিউটনের সূত্রগুলো ভরবেগের সংরক্ষণের তুলনায় অধিক মৌলিক নয়, যেখানে ভরবেগ নির্দেশকারী লব্ধি বল ধ্রুব নহে। একটি স্বতন্ত্র সিস্টেমের জন্য ভরবেগের সংরক্ষণ সর্বদাই সত্য যা লব্ধি বলের সাথে সম্পর্কিত নয়।
নির্দিষ্ট সংখ্যাক কণার ক্ষেত্রে, অন্যান্য কণার ন্যায় i কণার সমীকরণটি হবে—
যেখানে, pi = i কণার ভরবেগ, Fij = i কণার উপর j কণা দ্বারা প্রযুক্ত বল, এবং FE = বহিস্থ কোন উৎস দ্বারা ব্যবস্থাটির উপর প্রযুক্ত লব্ধি বল। i কণাটি কখনোই নিজেই নিজের উপর বল প্রয়োগ করে না। (দেখুন: Many-body problem বা বহু-বস্তু সমস্যা)
অয়লারের গতিসূত্রসমূহ নিউটনের সূত্রগুলোর অনুরূপ তবে এগুলো বিশেষকরে শুধু দৃঢ় বস্তুর গতির ক্ষেত্রে প্রয়োগ করা হয়। নিউটন-অয়লার সমীকরণ দৃঢ় বস্তুর উপর ক্রিয়াশীল বল ও বলের ভ্রামক বা টর্কসমুহকে একটি সমীকরণের মাধ্যমে সমন্বিত করে।
ঘূর্ণন গতির জন্য নিউটনের দ্বিতীয় সূত্রটির অনুরূপ সমীকরণটি হবে নিম্নরূপ—
এখানে বস্তুর উপর প্রযুক্ত টর্ক τ এর সাথে কৌণিক ভরবেগ L কে সমীকৃত করা হয়েছে।[১৭] সহজ কথায়, রৈখিক গতি সৃষ্টিকারী ফ্যাক্টরটি বল, অন্যদিকে কৌণিক গতি সৃষ্টিকারী ফ্যাক্টরটি হল টর্ক।
অনুরূপভাবে কৌণিক গতির ক্ষেত্রে ভরের সদৃশ রাশি হবে জড়তার ভ্রামক I (টেন্সর), যা ঘূর্ণনাক্ষের সাপেক্ষে বস্তুর ভরের বিন্যাস ও ঘূর্ণনাক্ষের অবস্থানের উপর নির্ভর করে। কৌণিক ত্বরণ α হল কৌণিক বেগের পরিবর্তনের হার।
পুণশ্চ, এই সমীকরণগুলো বিন্দুকণাতে বা দৃঢ় বস্তুর প্রতিটি বিন্দুতে প্রযুক্ত হয়।
অধিকন্তু ঘূর্ণন গতির ক্ষেত্রে নির্দিষ্ট সংখ্যক কণার ক্ষেত্রে i কণার জন্য সমীকরণটি হবে—
যেখানে, Li = i কণার কৌণিক ভরবেগ, τij = i কণা উপর j কণা দ্বারা প্রযুক্ত টর্ক, এবং τE = ব্যবস্থাটির উপর বহিস্থ কোন উৎস দ্বারা প্রযুক্ত লব্ধি টর্ক। i কণাটি কখনোই নিজেই নিজের উপর টর্ক প্রয়োগ করে না।[১৭] [১৮]
নিম্নের তালিকা লক্ষ্য করলে রৈখিক গতি ও ঘূর্ণন গতির সাদৃশ্য আরও স্পষ্ট হবে—
| রৈখিক গতি | ঘূর্ণন গতি | |
|---|---|---|
| i | রৈখিক সরণ | কৌণিক সরণ |
| ii | রৈখিক বেগ | কৌণিক বেগ |
| iii | রৈখিক ত্বরণ | কৌণিক ত্বরণ |
| iv | রৈখিক গতি সৃষ্টিকারী বল | কৌণিক গতি সৃষ্টিকারী টর্ক |
| v | রৈখিক ভরবেগ | কৌণিক ভরবেগ |
| vi | বস্তুর ভর | জড়তার ভ্রামক |
| vii | রৈখিক গতিশক্তি | ঘূর্ণন গতিশক্তি |
বিঃদ্রঃ উক্ত রাশিগুলো পারস্পরিক সদৃশ হলেও এরা কিন্তু পরস্পরের সমান নয়।
প্রয়োগ[সম্পাদনা]
নিচে একটি সরল দোলকের গতির আলোকে এবং সাইনোসাইডাল বৈশিষ্ট্য সম্পন্ন (সাইন তরঙ্গযুক্ত) ছন্দিত-স্পন্দকের গতির আলোকে নিউটনের গতিসূত্রগুলোর কিছু উদাহরণ দেওয়া হল[১৯]—
- সরল দোলক:
- এবং ছন্দিত স্পন্দক:
মহাকর্ষ বলের দরুন ভরসমূহের গতিকে ব্যাখ্যা করার জন্য, নিউটনের মহাকর্ষ সূত্রকে নিউটনের দ্বিতীয় গতিসূত্রের সাথে সমন্বিত করা যেতে পারে। নিচে দুটি উদাহরণ দেওয়া হল:
- R = R(r, t) (প্রতিরোধী বল) ভেক্টর ক্ষেত্রে উপর দিকে বায়ু প্রবাহের অনুকূলে m ভরের একটি বল নিক্ষেপ করা হল।
যেখানে, G = মহাকর্ষ ধ্রুবক, M = পৃথিবীর ভর, এবং A = +R/m = বায়ু প্রবাহের দিকে r অবস্থানে ও t সময়ে প্রাসটির (বলটির) ত্বরণ।
- এবং অভিকর্ষের দরুন পরস্পরের সাথে মিথষ্ক্রিয়ারত N সংখ্যক কণার চিরায়ত N-বস্তু সমস্যা হল N সংখ্যক দ্বিতীয় ক্রমের অরৈখিক সংযোজিত সাধারণ ব্যবকলন সমীকরণসমূহের (ODE) একটি সেট।
যেমন ব্যবকলন সমীকরণ:
যেখানে, i = 1, 2, …, N প্রতিটি কণার সাথে জড়িত ভর, অবস্থান ইত্যাদি রাশিকে চিহ্নিত করেছে।
বিশ্লেষণী বলবিদ্যা[সম্পাদনা]

ব্যবস্থাটির সীমাবদ্ধতার দরুন ত্রিমাত্রিক স্থানের তিনটি স্থানাঙ্কের প্রতিটির ব্যবহার করার প্রয়োজন নেই। যদি ব্যবস্থাটির স্বাধীনতার মাত্রা N হয়, তবে ব্যবস্থাটির রূপরেখার (configuration of the system) সংজ্ঞার জন্য, N সংখ্যক সাধারণীকৃত স্থানাঙ্ক q(t) = [q1(t), q2(t) ... qN(t)] এর একটি সেট ব্যবহার করা যেতে পারে। এগুলোকে চাপের দৈর্ঘ্য বা কোণ আকারে ব্যবহার করা যেতে পারে। কোন ব্যবস্থার গতির ব্যাখ্যায় এগুলো যথেষ্ট সরল, কারণ ব্যবস্থাটির গতির সীমা নির্ধারণে এদের স্বকীয় সীমাবদ্ধতার সুযোগ বিদ্যমান এবং স্থানাঙ্কগুলোর সংখ্যা সর্বনিম্ন হয়। সাধারণীকৃত স্থানাঙ্কগুলোর সময় অন্তরজ হল সাধারণীকৃত বেগ
অয়লার-ল্যাগ্রাঞ্জ সমীকরণ[২১]:—
যেখানে, ল্যাগ্রাঞ্জিয়ান হল q রূপরেখার (configuration) এবং +dq/dt এর পরিবর্তনে এর সময়-হার (এবং সম্ভাব্য সময় t) এর একটি ফাংশন।
ব্যবস্থাটির ল্যাগ্রাঞ্জিয়ান বসিয়ে, অতঃপর সমীকরণসমূহে এটা প্রতিস্থাপন করে এবং অংশক্রমে অন্তরজের মান নির্ণয় করে সরলীকরণ করলে স্থানাঙ্কে N যুক্ত দ্বিতীয় ক্রমের সাধারণ ব্যবকলনী সমীকরণসমূহের একটি সেট পাওয়া যাবে।
এখানে হল হ্যামিল্টনিয়ান যা q রূপরেখার (configuration) এবং সাধারণীকৃত-ভরবেগের একটি ফাংশন
- যেখানে, এবং
এখানে +∂/∂q = (+∂/∂q১, +∂/∂q২, …, +∂/∂qN) হল নির্দিষ্ট চলক এবং সম্ভাব্য সময় t এর সাপেক্ষে অংশক্রমে অন্তরজ ভেক্টরের একটি শর্টহ্যান্ড প্রতীক। (হর প্রতীকের উদাহরণের জন্য ম্যাট্রিক্স ক্যালকুলাস দেখুন।)
ব্যবস্থাটির হ্যামিল্টনিয়ান বসিয়ে, অতঃপর সমীকরণসমূহে এটা প্রতিস্থাপন করে এবং অংশক্রমে-অন্তরজের মান নির্ণয় করে সরলীকরণ করলে qi স্থানাঙ্কে এবং pi ভরবেগে 2N যুক্ত প্রথম ক্রমের সাধারণ ব্যবকলনী সমীকরণসমূহের একটি সেট পাওয়া যাবে।
- যেখানে, হল হ্যামিল্টনের মূল ফাংশন; একে চিরায়ত ক্রিয়াও বলা হয় যা L এর একটি ফাংশনা। এক্ষেত্রে ভরবেগ হল:
যদিও সমীকরণটির একটি সাধারণ আকার রয়েছে, তবুও প্রদত্ত হ্যামিল্টনিয়ানের কারণে N + 1 চলকগুলোতে এটি আসলে প্রথম ক্রমের একটি একক অরৈখিক অংশক্রমে ব্যবকলন সমীকরণ। S ক্রিয়াটি যান্ত্রিক ব্যবস্থার সংরক্ষিত রাশিগুলোকে সনাক্তকরণের অনুমতি দেয়, এমনকি যান্ত্রিক সমস্যাটি পূর্ণাঙ্গভাবে সমাধান করা না গেলেও। কারণ এমি নোয়েথারের উপপাদ্য অনুসারে, একটি ভৌত সিস্টেমের ক্রিয়ার যেকোন ব্যবকলনযোগ্য প্রতিসাম্যের একটি আনুষঙ্গিক সংরক্ষণ সূত্র বিদ্যমান।
ন্যূনতম ক্রিয়ার হ্যামিল্টনের মূল নীতি হিসেবে পরিচিত ভেরিয়েশনাল মূলনীতি থেকে সকল চিরায়ত সমীকরণসমূহ প্রতিপাদন করা যেতে পারে। রূপরেখা স্থান (configuration space) বরাবর সিস্টেমের পথরেখাকে বিবৃতকারী চিরায়ত সমীকরণ S ন্যূনতম ক্রিয়ার মধ্যে একটি।
তড়িৎ গতিবিদ্যা[সম্পাদনা]
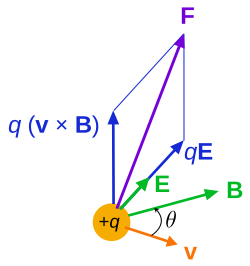
যুগপৎ ক্রিয়ারত E তড়িৎ ক্ষেত্র ও B চৌম্বক ক্ষেত্রে q আধানটি গতিশীল হলে এর উপর প্রযুক্ত লব্ধি বলকেই তড়িৎ গতিবিদ্যায় লরেঞ্জ বল বলা হয়। গাণিতিকভাবে[২৩]—
একে নিউটনের দ্বিতীয় সূত্রের সাথে সমন্বিত করলে কণার অবস্থানের ভিত্তিতে গতির প্রথম ক্রমের নিম্নোক্ত ব্যবকলনী সমীকরণটি পাওয়া যাবে:
অথবা এর যে ভরবেগ পাওয়া যাবে:
m ভরের এবং q চার্জের একটি কণার জন্য ল্যাগ্রাঞ্জিয়ান ব্যবহার করে (এবং উপরের ল্যাগ্রাঞ্জ সমীকরণসমূহ প্রয়োগ করে) একই সমীকরণ পাওয়া যাবে:[২৪]
যেখানে A এবং ϕ হল তড়িৎচুম্বকীয় স্কেলার এবং ভেক্টর বিভব ক্ষেত্র। ল্যাগ্রাঞ্জিয়ান একটি অতিরিক্ত ব্যাখ্যা নির্দেশ করে: ল্যাগ্রাঞ্জিয়ান বলবিদ্যায় শুধু শুধু ভরবেগ mv এর পরিবর্তে ক্যানোনিকাল ভরবেগ ব্যবহার করা হয়, যা নিম্নরূপ:
এটি কণার ভর এবং চার্জের মাধ্যমে মৌলিকভাবে নির্ধারিত চার্জিত কণার গতিকে বোঝায়। বলের সমীকরণ প্রতিপাদনের জন্য ল্যাগ্রাঞ্জিয়ান রাশিমালা প্রথম ব্যবহৃত হয়েছিল।
বিকল্পভাবে, হ্যমিল্টনিয়ান থেকে (এবং সমীকরণসমূহে প্রতিস্থাপনের মাধ্যমে) লরেঞ্জ বল সমীকরণ প্রতিপাদন করা যাবে;
যেখানে,
সাধারণ আপেক্ষিকতা[সম্পাদনা]
গতির জিওডেসিক সমীকরণ[সম্পাদনা]

উপরের সমীকরণসমূহ সমতলীয় স্থানকালে কার্যকর। বক্র স্থানকালে কোন সরল রেখা থাকে না, সরলরেখাকে সেখানে বক্র স্থানকালটির জিওডেসিক দ্বারা সাধারণিকরণ এবং প্রতিস্থাপন করা হয়। (জিওডেসিক হল কোন বক্ররেখার দুটি বিন্দুর ক্ষুদ্রতম দূরত্ব)। যার ফলে এরূপ স্থানকালের যে কোন কিছু গাণিতিকভাবে আরও জটিল হয়ে পড়ে। g মেট্রিক টেন্সর যুক্ত বক্র বহুভাঁজের দরুন মেট্রিকটি বৃত্তচাপ দৈর্ঘ্যের ধারণা দেয়। (বিস্তারিত জানতে রেখা উপাদান দেখুন)। ব্যবকলনী চাপ দৈর্ঘ্যকে নিচে দেওয়া হল:[২৬]
আর স্থানাঙ্ক ব্যবস্থায় জিওডেসিক সমীকরণটি হবে একটি দ্বিতীয় ক্রমের ব্যবকলনী সমীকরণ যার সাধারণ সমাধান হবে নিম্নোক্ত জিওডেসিক পরিবারভুক্ত:[২৭]
এখানে Γ μαβ হল একটি দ্বিতীয় প্রকার ক্রিস্টোফেল প্রতীক স্থানাঙ্ক ব্যবস্থার সাপেক্ষে যার মেট্রিক বিদ্যমান।
ভর-শক্তি বণ্টন প্রদানকারী আইনস্টাইনের ক্ষেত্র সমীকরণসমূহ (যাদেরকে পীড়ন-শক্তি টেন্সর T αβ এর মাধ্যমে প্রকাশ করা হয়) হল দ্বিতীয় ক্রমের অরৈখিক অংশক্রমে ব্যবকলনী সমীকরণ এবং এরা স্থানকালের বক্রতাকে পরোক্ষভাবে প্রকাশ করে যা মহাকর্ষীয় ক্ষেত্রের সমতূল্য (সমতার মূলনীতি দেখুন)। বক্র স্থানকালে ভরের পতন মহাকর্ষীয় ক্ষেত্রে ভরের পতনের সমতূল্য — কারণ মহাকর্ষ হল কল্পিত বল। বক্র স্থানকালে একটি জিওডেসিক থেকে অন্য জিওডেসিকের আপেক্ষিক ত্বরণকে নিম্নরূপ জিওডেসিক চ্যুতি সমীকরণের মাধ্যমে লেখা যায়:—
যেখানে ξα = x2α − x1α হল জিওডেসিকের মধ্যে বিচ্ছেদ ভেক্টর, +D/ds (not just +d/ds) হল কোভেরিয়েন্ট অন্তরজ এবং Rαβγδ হল ক্রিস্টোফেল প্রতীক সংবলিত রেইম্যান বক্রতা টেন্সর। অন্য কথায়, জিওডেসিক চ্যুতি সমীকরণ হল বক্র স্থানকালে ভরসমূহের গতির সমীকরণ যা তড়িচ্চুম্বকীয় ক্ষেত্রে আধানসমূহের লরেঞ্জ বল সমীকরণের সাথে তুলনাযোগ্য, [২৮]।
সমতলীয় স্থানকালের জন্য, মেট্রিকটি একটি ধ্রুব টেন্সর হয়, ফলে ক্রিস্টোফেল প্রতীক বিলুপ্ত হয়ে যায় এবং জিওডেসিক সমীকরণটির সরল রৈখিক সমাধান থাকে। ভরসমূহ নিউটনের মহাকর্ষ সূত্রানুসারে গতিশীল হলেও ব্যবস্থাটি সীমাবদ্ধ আচরণ করবে।
স্পিন গতিসম্পন্ন বস্তু[সম্পাদনা]
সাধরণ আপেক্ষিকতায় ঘূর্ণন গতিকে স্পিন টেন্সরসহ আপেক্ষিক কৌণিক ভরবেগ টেন্সরের মাধ্যমে বর্ণনা করা হয়। স্পিন টেন্সর গতির সমীকরণগুলোকে প্রকৃত সময়ের সাপেক্ষে কোভেরিয়েন্ট অন্তরজের অধীনে নিয়ে আসে। ম্যাথিসন-পাপাপেট্রো–ডিকসন সমীকরণ মহাকর্ষ ক্ষেত্রে গতিশীল বস্তুর স্পিন গতি ব্যাখ্যা করে।
তরঙ্গ ও ক্ষেত্রের সমতূল্য সমীকরণ[সম্পাদনা]
কণার বলবিদ্যা বর্ণনাকারী গতির সমীকরণগুলো যেখানে সংযোজিত সাধারণ ব্যবকলনী সমীকরণগুলোর ব্যবস্থা, সেখানে বিপরীতক্রমে এদেরই সমতূল্য যে সমীকরণগুলো তরঙ্গ ও ক্ষেত্রের গতিবিদ্যা অধিষ্ঠাকারী সেগুলো সর্বদাই আংশিক ব্যবকলনীয়, কারণ তরঙ্গ এবং ক্ষেত্র হল স্থান ও কালের ফাংশন। নির্দিষ্ট একটি সমাধানের জন্য সীমা শর্তগুলোকে সেই সাথে আদি শর্তগুলোকে স্পষ্টভাবে নির্ধারিত হওয়া প্রয়োজন।
তদুপরি কখনো কখনো নিম্নলিখিত প্রসঙ্গগুলোর ক্ষেত্রে তরঙ্গ ও ক্ষেত্র সমীকরণগুলোকেও গতির সমীকরণ বলা হয়।
ক্ষেত্র সমীকরণ[সম্পাদনা]
যেসব সমীকরণ কোন ক্ষেত্রের স্থানিক নির্ভরতা ও সময়ের বিবর্তনের বর্ণনা দেয় তাদেরকে ক্ষেত্র সমীকরণ বলা হয়। এগুলোর মধ্যে রয়েছে:—
- ম্যাক্সওয়েলের সমীকরণ যা তড়িচ্চুম্বকীয় ক্ষেত্রের বর্ণনা দেয়
- পয়সনের সমীকরণ যা নিউটনিয় মহাকর্ষ অথবা স্থির তড়িৎ ক্ষেত্র বিভবের বর্ণনা দেয়
- আইনস্টাইনের ক্ষেত্র সমীকরণ যা মহাকর্ষের বর্ণনা দেয় (নিউটনের মহাকর্ষ সূত্র দুর্বল মহাকর্ষীয় ক্ষেত্র এবং স্বল্প গতির কণার জন্য বিশেষভাবে কার্যকর)।
এই পরিভাষাটি সার্বজনীন নয়: যেমন নেভিয়ার-স্টোকস সমীকরণগুলো একটি প্রবাহীর জন্য বেগ ক্ষেত্র প্রতিষ্ঠা করলেও এদেরকে সচরাচর ক্ষেত্র সমীকরণ বলা হয় না; এই প্রসঙ্গে এরা বরং প্রবাহীটির ভরবেগকে নির্দেশ করায় এদেরকে ক্ষেত্র সমীকরণ না বলে ভরবেগের সমীকরণ বলা হয়।
তরঙ্গ সমীকরণ[সম্পাদনা]
তরঙ্গ গতির সমীকরণগুলোই তরঙ্গ সমীকরণ। তরঙ্গ সমীকরণের সমাধান থেকে বিস্তারের সময়-বিবর্তন এবং স্থানিক নির্ভরতা পাওয়া যায়। তরঙ্গ সমীকরণের সমাধানগুলো চলমান তরঙ্গ অথবা স্থির তরঙ্গ নির্দেশ করলে সীমা শর্তগুলো নির্ধারিত হয়।
গতির চিরায়ত সমীকরণ এবং ক্ষেত্র সমীকরণগুলো থেকে যান্ত্রিক, মহাকর্ষীয় তরঙ্গ এবং তড়িচ্চুম্বকীয় তরঙ্গ সমীকরণগুলো প্রতিপাদন করা যায়। সাধারণ রৈখিক তরঙ্গ সমীকরণের ত্রিমাত্রিক আকার হবে—
এখানে, v হল দশা বেগ এবং X = X(r, t) হল যেকোন যান্ত্রিক অথবা তড়িচ্চুম্বকীয় ক্ষেত্রের বিস্তার। X নিম্নোক্ত প্রসঙ্গগুলো নির্দেশ করে[২৯]:—
- কম্পমান দণ্ড বা রড, তার (wire), রশি (cable), পর্দা ইত্যাদির অনুদৈর্ঘ্য অথবা অনুপ্রস্থ সরণ,
- কোন মাধ্যমের তরঙ্গায়িত চাপ, শব্দ চাপ,
- E বা D তড়িৎ ক্ষেত্র, B বা H চৌম্বক ক্ষেত্র,
- কোন পরিবর্তী প্রবাহ তড়িৎ বর্তনীর বিভব V অথবা তড়িৎ প্রবাহ I
v(X) দ্বারা v কে প্রতিস্থাপন করে, অরৈখিক সমীকরণগুলো থেকে বিস্তারের উপর দশাবেগের নির্ভরতার প্রতিরূপ পাওয়া যায়। এছাড়াও বিশেষ বিশেষ কার্যক্ষেত্রের জন্য অন্যান্য রৈখিক এবং অরৈখিক তরঙ্গ সমীকরণসমূহ রয়েছে। উদাহরণ স্বরূপ কর্টেভ–ডি ভ্রাইস সমীকরণ দেখা যেতে পারে।
কোয়ান্টাম তত্ত্ব[সম্পাদনা]
কোয়ান্টম তত্ত্বে তরঙ্গ ও ক্ষেত্র উভয় ধারণাই দৃশ্যমান।
কোয়ান্টাম বলবিদ্যায় তরঙ্গ-কণা দ্বৈত নীতি অনুসারে কণাসমূহের তরঙ্গ সদৃশ ধর্ম বিদ্যমান। কোয়ান্টাম বলবিদ্যার আলোকে গতির চিরায়ত সমীকরণগুলোর সাথে তুলনীয় সমীকরণগুলো (যেমন: নিউটনের সূত্র, অয়লার-ল্যাগ্রাঞ্জ সমীকরণ, হ্যামিল্টন-জ্যাকোবি সমীকরণ ইত্যাদি) হল নিম্নোক্ত আকারের অতি সাধারণ শ্রোডিঙ্গার সমীকরণ:
এখানে Ψ হল সিস্টেমের তরঙ্গফাংশন, Ĥ হল কোয়ান্টাম হ্যামিল্টনিয়ান অপারেটর যা চিরায়ত বলবিদ্যায় নিছকই একটি ফাংশন এবং ħ হল প্লাঙ্ক ধ্রুবক h এর 2π দ্বারা ভাগ। হ্যামিল্টনিয়ান প্রতিস্থাপন করে একে সমীকরণটিতে সন্নিবেশ করলে একটি তরঙ্গ সমীকরণ পাওয়া যাবে; একে সমাধান করলে তরঙ্গফাংশনটি (Ψ) পাওয়া যাবে যা স্থান ও কালের একটি ফাংশন। ħ শূন্য হয় এমন সীমায় আনুষঙ্গিক মূলনীতিটি বিবেচনা করা হলে শ্রোডিঙ্গার সমীকরণটি হ্যামিল্টন-জ্যাকোবি সমীকরণে রূপান্তরিত (reduce) হবে।
আপেক্ষিক কিংবা অ-আপেক্ষিক কোয়ান্টাম তত্ত্বের সকল পরিপ্রেক্ষিতে শ্রোডিঙ্গারের সমীকরণের বিকল্প অনেক বিধি রয়েছে যেগুলো কোয়ান্টাম ব্যবস্থার সময়-বিবর্তন এবং আচরণ নিয়ন্ত্রণ করে। উদাহরণ স্বরূপ:—
- যদি গতীয় পর্যবেক্ষগুলোকে তাদের কোয়ান্টাম অপারেটর দ্বারা এবং চিরায়ত পয়সন বন্ধনীকে কমিউটেটর দ্বারা প্রতিস্থাপন করা হয় তবে হাইজেনবার্গের গতির সমীকরণটি অবস্থান, ভরবেগ এবং সময়ের মত চিরায়ত পর্যবেক্ষণগুলোর (observables) সময়-বিবর্তনের সদৃশ হবে,
- অবস্থান এবং ভরবেগকে সম-পদবিক্ষেপে সন্নিবেশের মাধ্যমে [[দশা-স্থান[স্থায়ীভাবে অকার্যকর সংযোগ] বিধি]] চিরায়ত হ্যামিল্টনিয়ান বলবিদ্যাকে ঘনিষ্ঠভাবে অনুসরণ করে,
- হ্যামিল্টনিয়ান অপেক্ষা ল্যাগ্রাঞ্জিয়ান প্রয়োগের পক্ষে অধিক গুরুত্ব দেওয়ার মাধ্যমে, ফাইনম্যানের [স্থায়ীভাবে অকার্যকর সংযোগ] সংযোগ|তারিখ=জানুয়ারি ২০২৩ |bot=InternetArchiveBot |ঠিক করার প্রচেষ্টা=yes }} সংযোগ|তারিখ=ডিসেম্বর ২০২২ |bot=InternetArchiveBot |ঠিক করার প্রচেষ্টা=yes }} সংযোগ|তারিখ=নভেম্বর ২০২২ |bot=InternetArchiveBot |ঠিক করার প্রচেষ্টা=yes }} সংযোগ|তারিখ=ফেব্রুয়ারি ২০২২ |bot=InternetArchiveBot |ঠিক করার প্রচেষ্টা=yes }} সংযোগ|তারিখ=ফেব্রুয়ারি ২০২২ |bot=InternetArchiveBot |ঠিক করার প্রচেষ্টা=yes }} সংযোগ|তারিখ=ফেব্রুয়ারি ২০২২ |bot=InternetArchiveBot |ঠিক করার প্রচেষ্টা=yes }} সংযোগ|তারিখ=জানুয়ারি ২০২২ |bot=InternetArchiveBot |ঠিক করার প্রচেষ্টা=yes }} সংযোগ|তারিখ=জানুয়ারি ২০২২ |bot=InternetArchiveBot |ঠিক করার প্রচেষ্টা=yes }} সংযোগ|তারিখ=অক্টোবর ২০২১ |bot=InternetArchiveBot |ঠিক করার প্রচেষ্টা=yes }} পথ সমাকলন বিধি ন্যূনতম ক্রিয়ার মূলনীতিকে কোয়ান্টাম বলবিদ্যায় এবং ক্ষেত্র তত্ত্বে সম্প্রসারিত করে।
আরও দেখুন[সম্পাদনা]
তথ্যসূত্র[সম্পাদনা]
- ↑ Encyclopaedia of Physics (second Edition), R.G. Lerner, G.L. Trigg, VHC Publishers, 1991, ISBN (Verlagsgesellschaft) 3-527-26954-1 (VHC Inc.) 0-89573-752-3
- ↑ Analytical Mechanics, L.N. Hand, J.D. Finch, Cambridge University Press, 2008, আইএসবিএন ৯৭৮-০-৫২১-৫৭৫৭২-০
- ↑ "Is the Solar System Stable?", Scott Tremaine, 2011
- ↑ University of Oxford
- ↑ Universities-of-Paris-I-XIII
- ↑ The transmission of Greek and Arabic learning
- ↑ The Britannica Guide to History of Mathematics, ed. Erik Gregersen
- ↑ Discourses, Galileo
- ↑ Dialogues Concerning Two New Sciences, by Galileo Galilei; translated by Henry Crew, Alfonso De Salvio
- ↑ Halliday, David; Resnick, Robert; Walker, Jearl (২০০৪-০৬-১৬)। Fundamentals of Physics (7 Sub সংস্করণ)। Wiley। আইএসবিএন 0-471-23231-9।
- ↑ Dynamics and Relativity, J.R. Forshaw, A.G. Smith, Wiley, 2009, আইএসবিএন ৯৭৮-০-৪৭০-০১৪৬০-৮
- ↑ M.R. Spiegel; S. Lipschutz; D. Spellman (২০০৯)। Vector Analysis। Schaum's Outlines (2nd সংস্করণ)। McGraw Hill। পৃষ্ঠা 33। আইএসবিএন 978-0-07-161545-7।
- ↑ Hanrahan, Val; Porkess, R (২০০৩)। Additional Mathematics for OCR। London: Hodder & Stoughton। পৃষ্ঠা 219। আইএসবিএন 0-340-86960-7।
- ↑ Keith Johnson (২০০১)। Physics for you: revised national curriculum edition for GCSE (4th সংস্করণ)। Nelson Thornes। পৃষ্ঠা 135। আইএসবিএন 978-0-7487-6236-1।
The 5 symbols are remembered by "suvat". Given any three, the other two can be found.
- ↑ 3000 Solved Problems in Physics, Schaum Series, A. Halpern, Mc Graw Hill, 1988, আইএসবিএন ৯৭৮-০-০৭-০২৫৭৩৪-৪
- ↑ ক খ An Introduction to Mechanics, D. Kleppner, R.J. Kolenkow, Cambridge University Press, 2010, p. 112, আইএসবিএন ৯৭৮-০-৫২১-১৯৮২১-৯
- ↑ ক খ "Mechanics, D. Kleppner 2010"
- ↑ "Relativity, J.R. Forshaw 2009"
- ↑ The Physics of Vibrations and Waves (3rd edition), H.J. Pain, John Wiley & Sons, 1983, আইএসবিএন ০-৪৭১-৯০১৮২-২
- ↑ R. Penrose (২০০৭)। The Road to Reality। Vintage books। পৃষ্ঠা 474। আইএসবিএন 0-679-77631-1।
- ↑ {{"Classical Mechanics 1973">Classical Mechanics (second edition), T.W.B. Kibble, European Physics Series, 1973, আইএসবিএন ০-০৭-০৮৪০১৮-০
- ↑ উদ্ধৃতি ত্রুটি:
<ref>ট্যাগ বৈধ নয়;Classical Mechanics 1973নামের সূত্রটির জন্য কোন লেখা প্রদান করা হয়নি - ↑ Electromagnetism (second edition), I.S. Grant, W.R. Phillips, Manchester Physics Series, 2008 আইএসবিএন ০-৪৭১-৯২৭১২-০
- ↑ Classical Mechanics (second Edition), T.W.B. Kibble, European Physics Series, Mc Graw Hill (UK), 1973, আইএসবিএন ০-০৭-০৮৪০১৮-০.
- ↑ Misner, Thorne, Wheeler, Gravitation
- ↑ C.B. Parker (১৯৯৪)। McGraw Hill Encyclopaedia of Physics (second সংস্করণ)। পৃষ্ঠা 1199। আইএসবিএন 0-07-051400-3।
- ↑ C.B. Parker (১৯৯৪)। McGraw Hill Encyclopaedia of Physics (second সংস্করণ)। পৃষ্ঠা 1200। আইএসবিএন 0-07-051400-3।
- ↑ J.A. Wheeler; C. Misner; K.S. Thorne (১৯৭৩)। Gravitation। W.H. Freeman & Co। পৃষ্ঠা 34–35। আইএসবিএন 0-7167-0344-0।
- ↑ H.D. Young; R.A. Freedman (২০০৮)। University Physics (12th সংস্করণ)। Addison-Wesley (Pearson International)। আইএসবিএন 0-321-50130-6।

![{\displaystyle M\left[\mathbf {r} (t),\mathbf {\dot {r}} (t),\mathbf {\ddot {r}} (t),t\right]=0\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c8af0a1cc881877bb37453609e50c61bd060c52)










































































![{\displaystyle L=L\left[\mathbf {q} (t),\mathbf {\dot {q}} (t),t\right]\,.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a30f80cbaa05dc7438902e9efb67fbad8ea096c)



![{\displaystyle H=H\left[\mathbf {q} (t),\mathbf {p} (t),t\right]\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aecc975922b815e9bb266e1e3158865400b860c7)


![{\displaystyle S[\mathbf {q} ,t]=\int _{t_{1}}^{t_{2}}L(\mathbf {q} ,\mathbf {\dot {q}} ,t)\,dt\,,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0dde602b4562727a396922b4b680ebe4afdc9828)












