স্থান-কাল
| স্থান-কাল |
|---|
| একটি সিরিজের অংশ |
 |
|
বিশেষ আপেক্ষিকতা সাধারণ আপেক্ষিকতা |
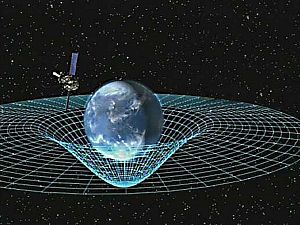
পদার্থবিজ্ঞানে স্থান-কাল বলতে যেকোন গাণিতিক মডেলকে বোঝায় যা সময় এবং স্থানকে মিলিয়ে স্থান-কাল সাংতত্যক নামক একটি একক কাঠামো গঠন করে। স্থান-কাল মূলত স্থানের তিনটি মাত্রার সাথে সময়কে যোগ করে একটি চতুর্মাত্রিক ধারণার জন্ম দেয়। ইউক্লিডীয় স্থান ধারণা অনুযায়ী স্থানকে ত্রিমাত্রিক এবং সময়কে একটি আলাদা মাত্রা হিসেবে বিবেচনা করা হতো। কিন্তু এই দুয়ের মিলন ঘটানোর মাধ্যমে পদার্থবিজ্ঞানীরা অনেকগুলো বৈজ্ঞানিক জটিলতা ও সমস্যার সমাধান করতে পেরেছেন। এই চতুর্মাত্রিক নীতি দিয়ে বৃহৎ স্কেলে মহাবিশ্বের গঠন থেকে শুরু করে অনেক ক্ষুদ্রাতিক্ষুদ্র বস্তু পর্যন্ত প্রায় সবারই পরিচালনার নীতি ব্যাখ্যা করা যায়।
ব্যাখ্যা
[সম্পাদনা]চিরায়ত বলবিদ্যা অনুসারে ইউক্লিডীয় স্থানে স্থান-কালের ব্যবহার যথাযথভাবে করা যায় কারণ সময় সেখানে ধ্রুবক এবং তা স্থানের ত্রিমাত্রিক গতি নিরপেক্ষ। এই তত্ত্ব কেবল নিম্ন গতির বস্তুর ক্ষেত্রেই প্রযোজ্য। আপেক্ষিকতাভিত্তিক তত্ত্বের কথা চিন্তা করলে, কালকে স্থানের থেকে আলাদা করে দেখার কোন উপায় নেই। কারণ এক্ষেত্রে কাল আলোর বেগের সাপেক্ষে ত্রিমাত্রিক স্থানের গতির উপর নির্ভরশীল। এছাড়া এটি তীব্র মহাকর্ষীয় ক্ষেত্রের উপরও নির্ভরশীল, কারণ তীব্র মহাকর্ষীয় ক্ষেত্র সময়ের গতিকে মন্থর করে দিতে পারে।
প্রকৃতিতে স্থান এবং সময় অবিচ্ছেদ্য ভাবে মিলে আছে। গাণিতিকভাবে এটা হল প্রসঙ্গ কাঠামো দাড়া বর্ণনাকৃত নানাবিধ ঘটনা। সাধারণত তিনটি স্থানিক মাত্রা (দৈর্ঘ্য, প্রস্থ, ঊচ্চতা) ও একটি সময়গত মাত্রা (সময়) প্রয়োজনীয়। কোন সুনির্দিষ্ট স্থান-কাল কে প্রকাশ করার জন্য মাত্রাগুলো প্রসঙ্গ কাঠামোর স্বাধীন উপাদান। যেমন পৃথিবীতে অক্ষাংশ ও দ্রাঘিমা দুটি মৌলিক মাত্রা যারা সম্মিলিত ভাবে একটি স্থান নির্দিষ্ট করে। অনেক সময় দেখা যায়, কোন পর্যবেক্ষক যা শুধু দৈর্ঘ্যর সাহায্যে পরিমাপ করছেন অন্য পর্যবেক্ষক হয়তো দৈর্ঘ্য ও সময় উভয়ের সাহায্যে পরিমাপ করছেন। যেকোন ঘটনাই স্থান-কাল নামক চতুর্মাত্রিক জগতে ঘটছে এটা ধরে নেয়াই হল আপেক্ষিকতার বিশেষ তত্ত্বের ফলাফল প্রকাশ করার সবচেয়ে সহজ এবং ভাল পদ্ধতি যেখানে তিনটি মাত্রা x, y, z স্থান নির্দেশ করে এবং চতুর্থ মাত্রা ict (i=(-1)1/2) সময় নির্দেশ করে। সময়ের মাত্রা t ব্যবহার না করে ict ব্যবহার করার কারণ হল নিচের সমীকরনটি লরেঞ্জ রূপান্তরের ফলে অপরিবর্তনীয় থাকে।
s2=x2+y2+z2-(ct)2
অর্থাৎ যদি কোন ঘটনা S প্রস্ংগ কাঠামোর সাপেক্ষে x, y, z, t এবং S1 প্রসংগ কাঠামোর সাপেক্ষে x1, y1, z1, t1 এ ঘটে তাহলে
s2=x2+y2+z2-(ct)2 =x12+y12+z12-(ct1)2
