সংরক্ষণ সূত্র

সংরক্ষণ সূত্র পদার্থবিজ্ঞানের এমন একটি সূত্র,যার বিবৃতি নিম্নরূপ -"বিচ্ছিন্ন অবস্থায় কোনো বস্তুর পরিমাপযোগ্য বৈশিষ্ট্য বিদ্যমান হলে, সময়ের সাথে অবস্থার পরিবর্তন হলেও কখনো পরিমাপযোগ্য বৈশিষ্ট্যের কোনো পরিবর্তন হয় না।"শক্তির সংরক্ষণশীলতা, সরলরৈখিক ভরবেগের সংরক্ষণশীলতা, কৌণিক ভরবেগের সংরক্ষণশীলতা ও তড়িৎ আধানের সংরক্ষণশীলতা সংরক্ষণ সূত্রের প্রমাণ। ভর, ত্রিমাত্রিক ক্ষেত্রের স্থানাঙ্কের চিহ্নের পরিবর্তন (Parity),লেপটন সংখ্যা, বেরিওন সংখ্যা, কোনো বস্তুর কোয়ার্ক দশায় গঠন (Strangeness) এবং শক্তিশালী আন্তঃক্রিয়ার কোয়ান্টাম প্রভাব ( Hypercharge) -এসব ক্ষেত্রেও সংরক্ষণ সূত্রের প্রভাব উল্লেখযোগ্য।

"মানের পরিবহন সমীকরণ" দ্বারা সংরক্ষণ সূত্র প্রকাশ করা হয়। একে আংশিক ব্যবকলনীয় সমীকরণের মাধ্যমেও প্রকাশ করা যায়। কোনো বিন্দুতে বা কোনো স্থানের অভ্যন্তরে সংরক্ষিত মান শুধু তখনই পরিবর্তিত হবে, যখন স্থানটির ভিতরে বা বাইরে সঞ্চারিত শক্তির মানের পরিবর্তন ঘটবে।

নোয়েথারের উপপাদ্য অনুযায়ী, প্রতিটি সংরক্ষণ সূত্রের সাথে প্রতিসমতা কোনো না কোনোভাবে সম্পর্কিত।

সংরক্ষণ সূত্র ও এর প্রায় "নির্ভুলতার" ক্ষেত্র

সংরক্ষণ সূত্র কোনো কোনো মানের ক্ষেত্রে কোনো কোনো সময় শতভাগ প্রযোজ্য হলেও বিশেষ দশায় বিশেষ ক্ষেত্রে এটি শতভাগ না হলেও প্রায় নির্ভুলভাবে প্রযোজ্য। এগুলো হলো-

(১) যান্ত্রিক শক্তির সংরক্ষণশীলতা

(২)স্থির ভরের সংরক্ষণশীলতা

(৩)বেরিওন সংখ্যার সংরক্ষণশীলতা

(৪)লেপটন সংখ্যার সংরক্ষণশীলতা

(৫)মৌলিক কণিকার দশার সংরক্ষণশীলতা

(৬)স্থানাঙ্ক চিহ্নের পরিবর্তন সমতা

প্রতিসমতার সাথে সম্পর্কিত সংরক্ষণ সূত্রের তালিকা

প্রতিসমতার মূলনীতি মেনে চলে, কিংবা প্রতিসমতার সাথে কোনো না কোনোভাবে সম্পৃক্ত সূত্রগুলোর তালিকা নিম্নরূপ:

(১) ভর-শক্তি সংরক্ষণ সূত্র (এক মাত্রার সমীকরণ, সময়কে অক্ষ বিবেচনা করে)

(২) রৈখিক ভরবেগের সংরক্ষণ সূত্র (তিন মাত্রার সমীকরণ, x,y,z -কে অক্ষ বিবেচনা করে)

(৩)কৌণিক ভরবেগের সংরক্ষণ সূত্র (তিন মাত্রার সমীকরণ, x,y,z অক্ষের ঘূর্ণন বিবেচনা করে)

(৪)ভরবেগ-কেন্দ্রের বেগের সংরক্ষণশীলতা সূত্র ( x,y,z অক্ষ বরাবর "লরেঞ্জ বুস্ট" বিবেচনা করে)

(৫)তড়িৎ আধানের সংরক্ষণশীলতা (চতুর্মাত্রিক ক্ষেত্র-সময় বিবেচনায় স্কেলার ক্ষেত্র; x,y, z অক্ষ ও সময়-কে একত্রে চারটি মাত্রা ধরে)

(৬)কালার-চার্জ সংরক্ষণশীলতা সূত্র (r,g, b অক্ষ বরাবর তিনটি মাত্রা বিবেচনা করে)

(৭) দুর্বল সম-স্পিন সংরক্ষণশীলতার সূত্র (দুর্বল আধানকে এক মাত্রা বিবেচনা করে)

(৮)সম্ভাবনার সংরক্ষণশীলতা সূত্র (সময় বিবর্তনের ক্ষেত্রে x,y,z মাত্রা বরাবর সম্ভাবনার সমষ্টি সর্বদাই ১)

ব্যবকলনীয় রূপ

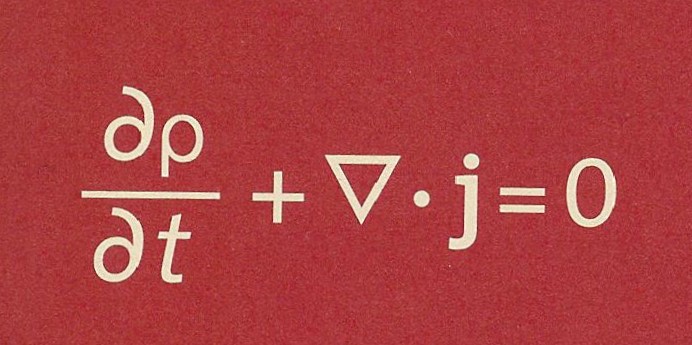"মানের পরিবহন" বলবিদ্যায় মান-পরিবহন সূত্র সংরক্ষণ সূত্রের অন্যতম ব্যবকলনীয় রূপ পরিগণিত হয়। যেমন- কোনো তড়িৎ আধান q এর সংরক্ষণশীলতা নিম্নরূপ:

${\frac {\partial \rho }{\partial t}}=-\nabla \cdot \mathbf {j} \,$

এখানে, ∇. হলো ডাইভারজেন্স অপারেটর, ρ হলো আধানের ঘনত্ব, j হলো আধানের ফ্লাস্ক আর t হলো সময়।

আমরা যদি ধরে নিই, আধানের গতি u সময় ও অবস্থানের একটি সচল ফাংশন, তাহলে:

$\mathbf {j} =\rho \mathbf {u}$

${\frac {\partial \rho }{\partial t}}=-\nabla \cdot (\rho \mathbf {u} )\,.$

একমাত্রিক ক্ষেত্রে, বক্ররৈখিক আংশিক ব্যবকলনীয় সমীকরণের অধিবৃত্তাকার রূপরেখার মাধ্যমে একে নিম্নরূপে প্রকাশ করা যায়:

$y_{t}+A(y)y_{x}=0$

এখানে অধীন চলক y হলো সংরক্ষিত মানের ঘনত্ব এবং A(Y) কারেন্ট জ্যাকোবিয়ান।

অসমজাতীয় ঘটনার ক্ষেত্রে সমীকরণটি নিম্নরূপ :

$y_{t}+A(Y)y_{x}=s$

অসমজাতীয় ঘটনার ক্ষেত্রে সমীকরণটি প্রকৃতপক্ষে সংরক্ষণ সূত্র মেনে চলে না ;এটিকে সমতার সমীকরণ অভিহিত করা যেতে পারে। নির্ভরশীল চলক y হলো অসংরক্ষিত মান এবং অসম ধ্রুবক s(x,y,t) হলো ডাইভারজেন্স। ভরবেগ, শক্তি (নেভিয়ার স্টোকস সমীকরণ) ও বিশৃঙ্খলা মাত্রা সাম্য সমীকরণ এর প্রকৃষ্ট উদাহরণ।