ত্বরণ
| ত্বরণ | |
|---|---|
 শূন্যস্থানে (বায়ুর বাধা নেই), পৃথিবী দ্বারা আকৃষ্ট সকল বস্তুর গতি নির্দিষ্ট হারে বৃদ্ধি পায়। | |
সাধারণ প্রতীক | a বা g (অভিকর্ষজ ত্বরণ) |
| এসআই একক | m/s2, m·s−2, m s−2 (মিটার প্রতি বর্গসেকেন্ড) |
অন্যান্য রাশি হতে উৎপত্তি | |
| মাত্রা | [LT-2] |
| চিরায়ত বলবিজ্ঞান |
|---|
| বিষয়ের উপর একটি ধারাবাহিকের অংশ |
বলবিজ্ঞানে ত্বরণ (Acceleration) হলো সময়ের সাথে কোনও বস্তুর বেগ পরিবর্তনের হার। এটি একটি সদিক রাশি বা ভেক্টর রাশি, অর্থাৎ এটির মান ও দিক উভয়ই বিদ্যমান।[১][২] কোনও বস্তুর ত্বরণের দিক সেই বস্তুর উপর প্রযুক্ত বলসমূহের লব্ধি বলের দিকে হয়। নিউটনের দ্বিতীয় সূত্রানুসারে,[৩] ত্বরণের মান হলো নিম্নোক্ত দুটি কারণের সম্মিলিত প্রভাব:
- বস্তুতে প্রযুক্ত সমস্ত বাহ্যিক নীট বলের ক্ষেত্রে — ত্বরণের মান নীট লব্ধি বলের সরাসরি সমানুপাতিক।
- বস্তুটির ভর — ত্বরণের মান বস্তুর ভরের ব্যস্তানুপাতিক।
ত্বরণের এসআই একক হলো মিটার প্রতি বর্গ সেকেন্ড (m⋅s−2, )।
উদাহরণস্বরূপ, যখন কোনও যানবাহন স্থির অবস্থা (একটি জড় প্রসঙ্গ কাঠামোর সাপেক্ষে বেগ শূন্য) থেকে শুরু করে এবং ক্রমবর্ধমান গতিতে একটি সরলরেখা বরাবর গতিশীল হয়, তখন এটি ভ্রমণের দিকের দিকে ত্বরান্বিত হয়। যানবাহনটি বাঁক নিলে নতুন দিক বরাবর ত্বরান্বিত হয় এবং গতি ভেক্টর পরিবর্তিত হয়। বর্তমান গতির দিকে গাড়ির ত্বরণকে রৈখিক (বা বৃত্তীয় গতির ক্ষেত্রে স্পর্শিনী) ত্বরণ বলা হয়, যার প্রতিক্রিয়া হিসেবে উপস্থিত যাত্রীরা পিছনের দিকে একটি বল অনুভব করেন। দিক পরিবর্তন করার সময়, কার্যকর ত্বরণকে কেন্দ্রমুখী (বা বৃত্তীয় গতির ক্ষেত্রে লাম্বিক) ত্বরণ বলা হয়, যার প্রতিক্রিয়া হিসাবে যাত্রীরা একটি অপকেন্দ্র বল অনুভব করেন। যদি গাড়ির গতি হ্রাস পায় তবে ত্বরণ বিপরীত দিকে হয় এবং গাণিতিকভাবে এটি ঋণাত্মক, যাকে কখনও কখনও মন্দন বলা হয় এবং মন্দনের প্রতিক্রিয়া হিসাবে যাত্রীরা তাদেরকে সামনে ঠেলে দেওয়ার মতো একটি জড়তা বল অনুভব করে। এই জাতীয় ঋণাত্মক ত্বরণ প্রায়শই মহাকাশযানে রেট্রোকেট জ্বালিয়ে অর্জন করা হয়।[৪] ত্বরণ এবং মন্দন উভয়ই একই বিবেচনা করা হয়, এগুলি উভয়ই বেগ পরিবর্তনের হার। এই ত্বরণগুলির প্রতিটি (স্পর্শিনী, কেন্দ্রমুখী, মন্দন) যাত্রীদের দ্বারা অনুভূত হয় যতক্ষণ না তাদের আপেক্ষিক (পার্থক্যমূলক) বেগ যানবাহনের সাপেক্ষে নিরপেক্ষ হয়।
সংজ্ঞা এবং বৈশিষ্ট্য[সম্পাদনা]

গড় ত্বরণ[সম্পাদনা]
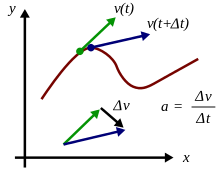
একটি বস্তুর গড় ত্বরণ হলো নির্দিষ্ট সময় ব্যবধানে বেগের পরিবর্তন এবং সময় ব্যবধান এর ভাগফলের সমান। গাণিতিকভাবে,
তাৎক্ষণিক ত্বরণ[সম্পাদনা]

- ত্বরণের অপেক্ষক a(t);
- ত্বরণের সমাকলন হলো বেগের অপেক্ষক v(t);
- এবং বেগের সমাকলন হলো সরণের অপেক্ষক s(t).
তাৎক্ষণিক ত্বরণ হলো, ক্ষুদ্রাতিক্ষুদ্র সময়ের ব্যবধানে গড় ত্বরণের সীমাস্থ মান। ক্যালকুলাসের ভাষায় তাৎক্ষণিক ত্বরণ হলো সময়ের সাপেক্ষে বেগ ভেক্টরের অন্তরজ:
যেহেতু ত্বরণকে সময় t এর সাপেক্ষে বেগ v এর অন্তরজ দ্বারা সংজ্ঞায়িত করা হয়, এবং বেগকে সময়ের সাপেক্ষে সরণ x এর অন্তরজের মাধ্যমে সংজ্ঞায়িত করা হয়, সেহেতু ত্বরণকে সময় t এর সাপেক্ষে সরণ x এর দ্বিতীয় অন্তরজ হিসেবে বিবেচনা করা যেতে পারে:
(এখানে এবং অন্য কোথাও যদি গতি একটি সরলরেখা বরাবর থাকে তবে সমীকরণগুলিতে ভেক্টর পরিমাণগুলিকে স্কেলার পরিমাণ দ্বারা প্রতিস্থাপিত করা যেতে পারে।)
ক্যালকুলাসের মৌলিক উপপাদ্য অনুযায়ী দেখা যায় যে, ত্বরণ ফাংশন a(t) এর সমাকলন হলো বেগের ফাংশন v(t); যা হলো, ত্বরণ-সময় (a vs. t) লেখচিত্রের বক্ররেখার নিচের ক্ষেত্রফল, যা বেগ নির্দেশ করে।
তেমনি, ত্বরণের অন্তরকলন জার্ক ফাংশন, j(t) এর সমাকলন ব্যবহার করে নির্দিষ্ট সময়ে ত্বরণ নির্ণয় করা যেতে পারে:
একক[সম্পাদনা]
ত্বরণের মাত্রা সমীকরণ হল বেগ (L/T) এবং সময়ের মাত্রার ভাগফল, অর্থাৎ L T−2 এবং এর এস.আই একক হলো মিটার প্রতি বর্গ সেকেন্ড (m s−2) বা মিটার প্রতি সেকেন্ড প্রতি সেকেন্ড; এবং সিজিএস একক হলো সেন্টিমিটার প্রতি বর্গ সেকেন্ড (cm s−2)।
অন্যান্য[সম্পাদনা]
বৃত্তীয় গতিতে চলমান একটি বস্তু - যেমন পৃথিবীকে প্রদক্ষিণকারী উপগ্রহ — গতির দিক পরিবর্তনের কারণে ত্বরান্বিত হয়, যদিও এর দ্রুতি স্থির থাকতে পারে। এক্ষেত্রে এটি কেন্দ্রমুখী (কেন্দ্রের দিকে নির্দেশিত) ত্বরণে চলছে।
যথাযথ ত্বরণ বা মুক্ত-পতনের শর্ত সাপেক্ষে একটি বস্তুর ত্বরণ অ্যাক্সিলারোমিটার নামক যন্ত্র দ্বারা পরিমাপ করা হয়।
চিরায়ত বলবিদ্যায় ধ্রুব ভরসম্পন্ন বস্তুর ক্ষেত্রে বস্তুর ভরকেন্দ্রের (ভেক্টর) ত্বরণ এর উপর প্রযুক্ত নীট বল ভেক্টরের (অর্থাৎ সমস্ত বলের যোগফল) সমানুপাতিক (নিউটনের দ্বিতীয় সূত্র):
যেখানে F হলো বস্তুর উপর প্রযুক্ত নীট বল, m হলো বস্তুর ভর, এবং a হলো ভরকেন্দ্রের ত্বরণ। বেগ যখন আলোর গতির কাছাকাছি পৌছায়, আপেক্ষিক প্রভাবগুলি ক্রমশ বৃদ্ধি পেতে থাকে।
স্পর্শিনী এবং অভিকেন্দ্র ত্বরণ[সম্পাদনা]


একটি কণার গতি একটি বক্রপথ বরাবর হলে সময়ের অপেক্ষক:
যেখানে v(t) হলো পথ বরাবর বেগ, এবং
নির্দিষ্ট মুহুর্তে গতির দিক নির্দেশকারী পথ বরাবর একটি একক ভেক্টর স্পর্শক। পরিবর্তনশীল বেগ v(t) এবং ut,এর পরিবর্তনশীল দিক বিবেচনা করে বক্রপথে চলমান একটি কণার ত্বরণ সময়ের দুটি অপেক্ষকের জন্য অন্তরকলনের চেইন বিধি [৫] ব্যবহার করে লেখা করা যেতে পারে:
যেখানে un হলো কণার প্রক্ষেপন পথের একক (অভ্যন্তরস্থ) সাধারণ ভেক্টর (principal normal নামেও পরিচিত), এবং r হলো t সময়ে বক্রপথের ব্যাসার্ধ। এই উপাংশগুলিকে বলা হয় স্পর্শিনী ত্বরণ এবং সাধারণ বা কেন্দ্রমুখী ত্বরণ।
ত্রি-মাত্রিক স্থান বক্ররেখার জ্যামিতিক বিশ্লেষণ, যা স্পর্শিনী, (মূল) সাধারণ এবং বাইনোমরাল ব্যাখ্যা করে, ফ্রেনেট-সেরেট সূত্রগুলি দ্বারা বর্ণিত হয়।[৬][৭]
বিশেষ ক্ষেত্র[সম্পাদনা]
সমত্বরণ[সম্পাদনা]
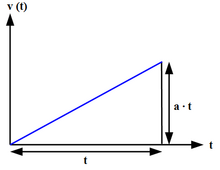
অভিন্ন বা ধ্রুবক ত্বরণ হল এক ধরনের গতি যাতে বস্তুর বেগ সমান সময়কালে সমান পরিমাণে পরিবর্তিত হয়।
অভিন্ন ত্বরণের একটি প্রায়শই উদ্ধৃত উদাহরণ হলো অভিন্ন মহাকর্ষীয় ক্ষেত্রে মুক্তভাবে পড়ন্ত বস্তু। গতির প্রতিরোধের অনুপস্থিতিতে একটি পতিত বস্তুর ত্বরণ কেবল মহাকর্ষ ক্ষেত্র প্রাবল্য g (মহাকর্ষের কারণে সৃষ্ট ত্বরণও বলা হয়) এর উপর নির্ভরশীল। নিউটনের দ্বিতীয় সূত্রানুযায়ী বস্তুর উপর প্রযুক্ত বল হলো:
সমত্বরণের ক্ষেত্রে সাধারণ বিশ্লেষণমূলক বৈশিষ্ট্যের কারণে সরণ, প্রাথমিক এবং সময় নির্ভর বেগ এবং অতিবাহিত সময়ের সাথে ত্বরণ সম্পর্কিত সহজ সূত্র রয়েছে:[৮]
যেখানে
- হলো অতিক্রান্ত সময়,
- হলো উৎস থেকে আদি সরণ,
- হলো তম সময়ে উৎস থেকে সরণ,
- হলো আদিবেগ,
- হলো তম সময়ে বেগ, এবং
- হলো সমত্বরণ
বিশেষত, গতিকে দুটি লম্ব অংশে সমাধান করা যেতে পারে, একটি হলো ধ্রুব বেগ এবং অন্যটি উপরের সমীকরণ অনুসারে। গ্যালিলিও যেমন দেখিয়েছিলেন, নীট ফলাফল হলো পরাবৃত্তীয় গতি, যা পৃথিবী পৃষ্ঠের নিকটবর্তী শূন্যস্থানে একটি প্রাসের গতিপথ বর্ণনা করে।[৯]
বৃত্তীয় গতি[সম্পাদনা]
সমবৃত্তীয় গতির ক্ষেত্রে, যেখানে একটি বৃত্তাকার পথ ধরে ধ্রুব গতিতে এগিয়ে চলেছে, একটি কণা বেগ ভেক্টরের দিকের পরিবর্তনের ফলে একটি ত্বরণ অনুভব করে, যদিও এর মান স্থির থাকে। সময়ের সাপেক্ষে একটি বক্ররেখার বিন্দুর অবস্থানের অন্তরকলন, অর্থাৎ এর গতিবেগ সর্বদা বক্ররেখার ঠিক স্পর্শক বরাবর এবং এই বিন্দুর ব্যাসার্ধের সাথে লম্ব বরাবর অবস্থান করে। যেহেতু সমগতিতে স্পর্শকীয় দিকের গতিবেগ পরিবর্তন হয় না, ত্বরণ অবশ্যই ব্যাসার্ধের দিকে হতে হবে, যা বৃত্তের কেন্দ্রের দিকে নির্দেশ করে। এই ত্বরণটি ক্রমাগত বেগের ভেক্টরকে প্রতিবেশী বিন্দুতে স্পর্শক হওয়ার জন্য পরিবর্তন করে, যার ফলে গতিবেগের সাথে বেগ ভেক্টরটিকে ঘোরানো হয়।
• নির্দিষ্ট দ্রুতি এর ক্ষেত্রে জ্যামিতিকভাবে সংঘটিত ত্বরণ (কেন্দ্রমুখী ত্বরণ) বৃত্তের ব্যাসার্ধ এর সমানুপাতিক, এবং এই দ্রুতির বর্গের হারে বৃদ্ধি পায়,
• মনে রাখবেন যে, প্রদত্ত কৌণিক বেগ এর জন্য, কেন্দ্রমুখী ত্বরণ ব্যাসার্ধ এর সাথে সরাসরি সমানুপাতিক। এর কারণ ব্যাসার্ধ এর উপর বেগ এর নির্ভরতা।
কেন্দ্রমুখী ত্বরণ ভেক্টরকে পোলার উপাংশে প্রকাশ করার ক্ষেত্রে, যেখানে হলো বৃত্তের কেন্দ্র থেকে কণা পর্যন্ত দুরত্বের মানসম্পন্ন একটি ভেক্টর, এবং ত্বরণের দিক বিবেচনা করলে দাঁড়ায়,
ঘূর্ণনের ক্ষেত্রে সচরাচর একটি কণার দ্রুতি বিন্দুর দূরত্ব এর সাপেক্ষে কৌণিক দ্রুতি হিসাবে প্রকাশ করা যেতে পারে
এভাবে,
এই ত্বরণ এবং কণার ভর বৃত্তাকার কেন্দ্রের দিকে নির্দেশিত প্রয়োজনীয় কেন্দ্রমুখী বল নির্ধারণ করে, যা এটিকে সমবৃত্তীয় গতিতে রাখার জন্য নীট বল হিসাবে এই কণার উপর প্রযুক্ত হয়। তথাকথিত 'কেন্দ্রবিমুখী বল' বস্তুর উপর বাহ্যিকভাবে কাজ করে বলে মনে হয়, যা একটি তথাকথিত নকল বল যা বস্তুর রৈখিক ভরবেগের কারণে বস্তুর প্রসঙ্গ কাঠামোতে অনুভূত হয়, যা গতির বৃত্তের জন্য একটি ভেক্টর স্পর্শক হিসেবে থাকে।
অসম বৃত্তীয় গতিতে, অর্থাৎ, যেখানে বক্রপথের গতি পরিবর্তিত হচ্ছে, বক্ররেখার স্পর্শক বরাবর ত্বরণের অ-শূন্য উপাংশ রয়েছে, এবং প্রধান প্রান্তিকের মধ্যে সীমাবদ্ধ নয়, যা দোলকের বৃত্তের কেন্দ্রে পরিচালিত করে, তা কেন্দ্রমুখী ত্বরণের ব্যাসার্ধ নির্ধারণ করে। স্পর্শিনী উপাংশটি কৌণিক ত্বরণ এবং ব্যাসার্ধ এর গুণফলের সমান,
ত্বরণের স্পর্শিনী উপাংশটির চিহ্ন কৌণিক ত্বরণের () চিহ্ন দ্বারা নির্ধারিত হয় এবং স্পর্শকটি সর্বদা ব্যাসার্ধ ভেক্টরের ডান কোণে নির্দেশিত হয়।
আপেক্ষিকতার সাথে সম্পর্ক[সম্পাদনা]
বিশেষ আপেক্ষিকতা[সম্পাদনা]
আপেক্ষিকতার বিশেষ তত্ত্বটি শূন্যস্থানে অন্য কোনো বস্তুর সাপেক্ষে আলোর বেগে চলমান বস্তুর আচরণ বর্ণনা করে। নিউটনীয় বলবিজ্ঞান হুবহু বাস্তবের সান্নিধ্য হিসাবে প্রকাশিত হয়েছে, নিম্ন গতিতে দুর্দান্ত নির্ভুলতার জন্য কার্যকর। আপেক্ষিক গতি আলোর গতির কাছাকাছি বৃদ্ধি পাওয়ার সাথে সাথে ত্বরণ আর চিরায়ত সমীকরণ অনুসরণ করে না।
আলোর গতির কাছাকাছি পৌঁছালে, প্রদত্ত বল দ্বারা উৎপাদিত ত্বরণ হ্রাস পায়, এবং আলোর গতির কাছে পৌঁছানোর সাথে সাথে অপরিমেয় রূপে ক্ষুদ্র হয়ে যায়; ভরসম্পন্ন কোনও বস্তু এই গতির দিকে তাত্পর্যপূর্ণভাবে আগাতে পারে, তবে কখনও সেই গতিতে পৌঁছাতে পারে না।
সাধারণ আপেক্ষিকতা[সম্পাদনা]
কোনও বস্তুর গতির অবস্থা জানা না থাকলে, পর্যবেক্ষিত কোনো বল মাধ্যাকর্ষণ নাকি ত্বরণের কারণে তা পার্থক্য করা অসম্ভব — কারণ মাধ্যাকর্ষণ এবং প্রারম্ভিক ত্বরণের প্রভাব অভিন্ন এবং তার মধ্যে পার্থক্য করা অসম্ভব। আলবার্ট আইনস্টাইন এটিকে সমতুল্য নীতি হিসাবে অভিহিত করেছেন এবং বলেছিলেন যে কেবল পর্যবেক্ষকরা যারা মহাকর্ষের বলসহ কোনও ধরনের বলের প্রভাব বোধ করেন না তাদের ক্ষেত্রে এই সিদ্ধান্ত যুক্তিযুক্ত যে তারা ত্বরান্বিত হচ্ছে না।[১০]
রূপান্তর[সম্পাদনা]
| মূল মান | (গ্যাল, বা সেমি/সে2) | (ফুট/সে2) | (মি/সে2) | (আদর্শ অভিকর্ষ বল, g0) |
|---|---|---|---|---|
| ১ গ্যাল, বা সেমি/সে2 | ১ | ০.০৩২৮০৮৪ | ০.০১ | ০.০০১০১৯৭২ |
| ১ ফুট/সে2 | ৩০.৪৮০০ | ১ | ০.৩০৪৮০০ | ০.০৩১০৮১০ |
| ১ মি/সে2 | ১০০ | ৩.২৮০৮৪ | ১ | ০.১০১৯৭২ |
| ১ g0 | ৯৮০.৬৬৫ | ৩২.১৭৪০ | ৯.৮০৬৬৫ | ১ |
আরও দেখুন[সম্পাদনা]
তথ্যসূত্র[সম্পাদনা]
- ↑ Bondi, Hermann (১৯৮০)। Relativity and Common Sense। Courier Dover Publications। পৃষ্ঠা 3। আইএসবিএন 978-0-486-24021-3।
- ↑ Lehrman, Robert L. (১৯৯৮)। Physics the Easy Way। Barron's Educational Series। পৃষ্ঠা 27। আইএসবিএন 978-0-7641-0236-3।
- ↑ Crew, Henry (২০০৮)। The Principles of Mechanics। BiblioBazaar, LLC। পৃষ্ঠা 43। আইএসবিএন 978-0-559-36871-4।
- ↑ Raymond A. Serway; Chris Vuille; Jerry S. Faughn (২০০৮)। College Physics, Volume 10। Cengage। পৃষ্ঠা 32। আইএসবিএন 9780495386933।
- ↑ Weisstein, Eric W.। "Chain Rule"। Wolfram MathWorld। Wolfram Research। সংগ্রহের তারিখ ২ আগস্ট ২০১৬।
- ↑ Larry C. Andrews; Ronald L. Phillips (২০০৩)। Mathematical Techniques for Engineers and Scientists। SPIE Press। পৃষ্ঠা 164। আইএসবিএন 978-0-8194-4506-3।
- ↑ Ch V Ramana Murthy; NC Srinivas (২০০১)। Applied Mathematics। New Delhi: S. Chand & Co.। পৃষ্ঠা 337। আইএসবিএন 978-81-219-2082-7।
- ↑ Keith Johnson (২০০১)। Physics for you: revised national curriculum edition for GCSE (4th সংস্করণ)। Nelson Thornes। পৃষ্ঠা 135। আইএসবিএন 978-0-7487-6236-1।
- ↑ David C. Cassidy; Gerald James Holton; F. James Rutherford (২০০২)। Understanding physics। Birkhäuser। পৃষ্ঠা 146। আইএসবিএন 978-0-387-98756-9।
- ↑ Brian Greene, The Fabric of the Cosmos: Space, Time, and the Texture of Reality, page 67. Vintage আইএসবিএন ০-৩৭৫-৭২৭২০-৫
বহিঃসংযোগ[সম্পাদনা]
- Acceleration Calculator সাধারণ ত্বরণ একক রূপান্তরকারী
- Acceleration Calculator ত্বরণ রূপান্তর ক্যালকুলেটর মিটার প্রতি বর্গ সেকেন্ড, কিলোমিটার প্রতি বর্গ সেকেন্ড মিলিমিটার প্রতি বর্গ সেকেন্ড ইত্যাদি একককে রূপান্তর করে।


















![{\displaystyle {v^{2}}(t)={v_{0}}^{2}+2\mathbf {a\cdot } [\mathbf {s} (t)-\mathbf {s} _{0}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dad0ae6651010935bfa411ced51abe128c9e8647)



















