কোয়ান্টাম বিজড়ন
| কোয়ান্টাম বলবিজ্ঞান |
|---|
| বিষয়ক একটি ধারাবাহিকের অংশ |
কোয়ান্টাম বিজড়ন (ইংরেজি: Quantum entanglement) হল এমন একটি ভৌত ঘটনা যেখানে একাধিক কণার একটি সমবায় এমনভাবে উৎপন্ন হয়, এবং যেখানে কণাগুলি এমনভাবে পরস্পরের সঙ্গে আন্তঃক্রিয়া সম্পাদন করে কিংবা স্থানিক নৈকট্য ভাগাভাগি করে, যাতে যেকোনও একটি কণার কোয়ান্টাম অবস্থা অন্য কণাগুলির সাপেক্ষে স্বাধীনভাবে ব্যাখ্যা করা যায় না, এবং তার পরিবর্তে সম্পূর্ণ সমবায়টির কোয়ান্টাম অবস্থা একত্রে ব্যাখা করতে হয়। কণাগুলি পরস্পরের থেকে অতিবৃহৎ দূরত্বে অবস্থান করলেও এইরূপ বিজড়িত অবস্থা বজায় থাকে। কোয়ান্টাম বিজড়নের বিষয়টি চিরায়ত ও কোয়ান্টাম বলবিজ্ঞানের মধ্যে অসমতার কেন্দ্রে অবস্থিত। অর্থাৎ বিজড়ন হল কোয়ান্টাম বলবিজ্ঞানের একান্তই নিজস্ব একটি মৌলিক ধর্ম, যেটি চিরায়ত বলবিজ্ঞানে বিদ্যমান নয়।
বিজড়িত কণাসমূহের অবস্থান, ভরবেগ, স্পিন, মেরুকরণ (পোলারাইজেশন) ইত্যাদি ভৌত ধর্মগুলি পরিমাপ করলে কিছু কিছু ক্ষেত্রে ঐ পরিমাপকৃত মানগুলিকে একে অপরের সাথে সম্পূর্ণ সহ-সম্পর্কিত অবস্থায় পাওয়া যায়। উদাহরণস্বরূপ কোনও একটি প্রক্রিয়ায় যদি দুইটি বিজড়িত কণা এমনভাবে উৎপন্ন হয় যে তাদের মোট জ্ঞাত ঘূর্ণন বা স্পিন শূন্য হয়, তবে একটি কণার স্পিন যদি কোনও অক্ষের সাপেক্ষে ঘড়ির কাঁটার দিকে পাওয়া যায়, তবে অন্য কণাটির স্পিন অবশ্যই সেই অক্ষের সাপেক্ষে ঘড়ির কাঁটার বিপরীতে হবে। তবে এই আচরণটি আপাতদৃষ্টিতে এক ধরনের কূটাভাসমূলক (পরস্পরবিরোধী) ক্রিয়ার জন্ম দেয়: কোনও কণার ধর্মের যেকোনও ধরনের পরিমাপ ঐ কণার জন্য একটি অপ্রত্যাবর্তী তরঙ্গ অপেক্ষক ধস ঘটায় এবং আদি কোয়ান্টাম অবস্থাটি পরিবর্তন করে ফেলে। বিজড়িত কণাগুলির ক্ষেত্রে ঐ ধরনের পরিমাপ বিজড়িত ব্যবস্থাটিকে সামগ্রিকভাবে প্রভাবিত করে।
১৯৩৫ সালে আলবার্ট আইনস্টাইন, বরিস পোদলস্কি ও নেথান রোজেন একটি গবেষণাপত্রে এই ঘটনাগুলি নিয়ে লেখেন।[১] এর স্বল্পকাল পরেই এরউইন শ্র্যোডিঙার বিষয়টির উপর একাধিক গবেষণাপত্র প্রকাশ করেন[২][৩] এমন একটি ঘটনাটির বর্ণনা দেন, যা বর্তমানে আইনস্টাইন-পোদলস্কি-রোজেন কূটাভাস হিসেবে পরিচিত। আইনস্টাইন ও তাঁর সহযোগীরা এই ধরনের আচরণ অসম্ভব হিসেবে গণ্য করতেন, কেননা এটি কার্যকারণ সম্পর্কের স্থানিক বাস্তবতাবাদ লঙ্ঘন করেছিল। আইনস্টাইন ঘটনাটিকে "ভৌতিক দূরবর্তী কাজ" নামে অভিহিত করেন। ("spooky action at a distance")[৪] এবং এই যুক্তি দেন যে এর পরিণামস্বরূপ কোয়ান্টাম বলবিজ্ঞানের স্বীকৃত সূত্রায়নটি অবশ্যই অসম্পূর্ণ।
কিন্তু পরবর্তীকালে কিছু পরীক্ষায় কোয়ান্টাম বলবিজ্ঞানের এই আপাত স্বজ্ঞাবিরোধী ভবিষ্যৎবাণীগুলি যাচাই করা হয়।[৫][৬][৭] এই পরীক্ষাগুলিতে বিজড়িত কণাসমূহের মেরুকরণ বা স্পিন পৃথক পৃথক অবস্থানে পরিমাপ করা হয়, যা কিনা পরিসংখ্যানিকভাবে বেলের অসমতা লঙ্ঘন করে। প্রথম দিকের পরীক্ষাগুলিতে একটি বিন্দুতে প্রাপ্ত ফলাফল যে অগোচরে দূরবর্তী দ্বিতীয় বিন্দুটিতে সম্প্রচারিত হয়ে যায়নি ও সেটির ফলাফল প্রভাবিত করেনি, সে ব্যাপারটি নাকচ করা সম্ভব হয়নি।[৭] তবে তথাকথিত "ফাঁকফোঁকরবিহীন" বেলের পরীক্ষাগুলি সম্পাদন করা সম্ভব হয়েছে যেখানে অবস্থানগুলি এমন যথেষ্ট পরিমাণ দূরত্বে পৃথক যে পরিমাপগুলির মধ্যে সময়ের ব্যবধানের তুলনায় আলোর দ্রুতিতে যোগাযোগ স্থাপন করতে অনেক দীর্ঘতর সময় - একটি ক্ষেত্রে ১০ হাজার গুণ বেশি সময় - লাগত।[৬][৫]
কোয়ান্টাম বলবিজ্ঞানের ব্যাখ্যাসমূহের কয়েকটি অনুযায়ী কোনও পরিমাপের প্রভাব তাৎক্ষণিকভাবে ঘটে। অন্যান্য কিছু ব্যাখ্যাতে তরঙ্গ অপেক্ষকের ধসের ঘটনাটিকে স্বীকার করা হয় না, বরং আদৌ কোনও "প্রভাব" আছে কি না, তা নিয়েই প্রশ্ন তোলা হয়। তবে সবগুলি ব্যাখ্যাই সহমত যে বিজড়ন পরিমাপগুলির মধ্যে সহসম্পর্ক সৃষ্টি করে এবং এভাবে বিজড়িত কণাগুলির মধ্যে পারস্পরিক তথ্যকে কাজে লাগানো সম্ভব, কিন্তু আলোর চেয়ে বেশি দ্রুতিতে তথ্যের সম্প্রচার অসম্ভব।[৮][৯]
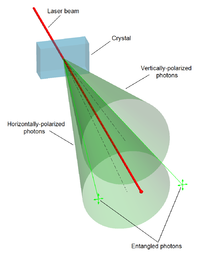
কোয়ান্টাম বিজড়ন পরীক্ষার মাধ্যমে ফোটন[১০], নিউট্রিনো[১১][১২] ইলেকট্রন,[১৩][১৪] এমনকি বাকিগোলকের মতো বড় অণু[১৫][১৬] ও ক্ষুদ্র হীরার[১৭][১৮] মাধ্যমে প্রদর্শন করা হয়েছে। কোয়ান্টাম যোগাযোগ, কোয়ান্টাম পরিগণন ও কোয়ান্টাম রাডার প্রযুক্তিগুলিতে বিজড়নের প্রয়োগ গবেষণা ও বিকাশের একটি অত্যন্ত সক্রিয় ক্ষেত্র।
"বিজড়িত ফোটনসমূহ নিয়ে পরীক্ষানিরীক্ষার মাধ্যমে বেল অসমতাগুলির লঙ্ঘন প্রতিষ্ঠান করা ও কোয়ান্টাম তথ্যবিজ্ঞানের অগ্রপথিকসুলভ গবেষণাকর্মের জন্য" ২০২২ সালে যৌথভাবে ফরাসি পদার্থবিজ্ঞানী আলাঁ আস্পে, মার্কিন পদার্থবিজ্ঞানী জন ক্লাউজার ও অস্ট্রীয় বিজ্ঞানী আন্টন সাইলিঙারকে পদার্থবিজ্ঞানে নোবেল পুরস্কার প্রদান করা হয়।[১৯]
গবেষণার ইতিহাস
[সম্পাদনা]কোয়ান্টাম বিজড়ন একটি অদ্ভূত ঘটনা যেখানে দুই বা ততোধিক কণা একটি তথাকথিত বিজড়িত অবস্থাতে বিদ্যমান থাকে। এই অস্বাভাবিক পরিস্থিতিতে একটি কণার উপর সাধিত কোনও ক্রিয়ার প্রভাব তাৎক্ষণিকভাবে, আপাতদৃষ্টিতে আলোর দ্রুতির চেয়েও বহুগুণ বেশি দ্রুতিতে সমগ্র বিজড়িত সমবায়টির ভেতর দিয়ে প্রবাহিত হয়ে অপর কণাটির আচরণ ভবিষ্যৎবাণী করতে পারে, এমনকি যদি সেগুলি একে অপরের থেকে বহু লক্ষ কিলোমিটার দূরেও অবস্থিত হয়। যদি কোনও পর্যবেক্ষক এরকম একটি কণার অবস্থা নির্ণয় করেন, তাহলে সেই কণাটির সাথে বিজড়িত প্রতিবিম্বরূপী কণাটি বা কণাগুলি সেই অবস্থাটির প্রতিফলন দেখাবে, এবং সেগুলি বহুদূরে, এমনকি মহাবিশ্বের অপর প্রান্তের কোনও ছায়াপথেও অবস্থান করতে পারে। এই অদ্ভূত ঘটনাটি আধুনিক কোয়ান্টাম প্রযুক্তিগুলির ক্ষেত্রে একটি মৌলিক বিষয়ে পরিণত হয়েছে। এই ঘটনাটি এতটাই স্বজ্ঞাবিরোধী ও আপাতদৃষ্টিতে অসম্ভব যে আলবার্ট আইনষ্টাইন এটিকে "দূরবর্তী ভৌতিক ঘটনা" বলে তিরস্কার করেছিলেন।[২০]
১৯৩০-এর দশকে আলবার্ট আইনস্টাইন বিশ্বাস করতেন যে অতিবৃহৎ গ্রহ থেকে ক্ষুদ্রাতিক্ষুদ্র কণা পর্যন্ত সমস্ত বস্তু এমন সব মৌলিক ধর্মের অধিকারী যেগুলিকে সুস্পষ্ট পর্যবেক্ষণের মাধ্যমে নির্ণয় করা সম্ভব। যদি আইনষ্টাইনের এই অনুমান সঠিক হয়, তাহলে কোয়ান্টাম বলবিজ্ঞানীরা অতিপারমাণবিক বিশ্বের কণাগুলির সহজাত কিন্তু অদ্যাবধি-অনাবিষ্কৃত কিছু "লুক্কায়িত চলরাশি"র ব্যাখ্যা দিতে পারেননি বলেই একটি অলীক বিভ্রম হিসেবে কোয়ান্টাম বিজড়ন দৃষ্ট হয়। যদি কোয়ান্টাম বিজড়িত কণাগুলির অবস্থা প্রাকনির্দিষ্ট করে দেওয়া যায়, তাহলে সেগুলিকে বিশাল দূরত্বে বিচ্ছিন্ন করে তারপরে পরিমাপ করলেও কীভাবে সেগুলি একে অপরের অবস্থার প্রতিফলন ঘটাতে পারে, সে ব্যাপারটি লুক্কায়িত চলরাশির মাধ্যমে সুন্দর করে ব্যাখ্যা করা সম্ভব। কেননা অন্যথায় তাদের মধ্যে তথ্য আলোর চেয়েও দ্রুত গতিবেগে গমন করবে, যা কিনা পদার্থবিজ্ঞানের সবচেয়ে মৌলিক একটি বিশ্বাস বা মতবাদের চরম লঙ্ঘন হবে। কিন্তু আইনষ্টাইনের এই লুক্কায়িত চলরাশি তত্ত্বটি নিলস বোর, এরভিন শ্র্যোডিঙার ও অন্যান্য পদার্থবিজ্ঞানীরা প্রত্যাখ্যান করেন। তাদের মতে বাস্তবতা সহজাতভাবেই অস্পষ্ট এবং কণাগুলিকে কেবল পরিমাপ করতে গেলে তবেই সেগুলি কিছু বিশেষ ধর্ম অর্জন করে।[২০]
এর প্রায় ৩ দশক পর ১৯৬০-এর দশকে উত্তর আইরীয় পদার্থবিজ্ঞানী জন স্টুয়ার্ট বেল কোয়ান্টাম বিজড়নের ঘটনাটিকে আবার গভীরভাবে অনুসন্ধান করেন। তিনি এইরূপ বিজড়নের "ভৌতিকতা" বাস্তবতার মৌলিক প্রকৃতি সম্পর্কে আমাদেরকে কী বলে, তা বুঝতে চেয়েছিলেন। তিনি আইনষ্টাইন ও তাঁর সহযোগী পদার্থবিজ্ঞানী বরিস পোদলস্কি ও নেথান রোজেনের প্রস্তাবকৃত একটি ধারণার সম্প্রসারণ সাধন করেন এবং কিছু চিন্তন পরীক্ষার মাধ্যমে দেখান যে যদি তাঁদের প্রস্তাবিত লুক্কায়িত চলরাশির অস্তিত্ব থাকত, তাহলে একাধিক কোয়ান্টাম বিজড়িত কণাজোড়কে সাবধানতার সাথে পরিমাপ করে ঐসব লুক্কায়িত রাশির উপস্থিতি পরীক্ষার মাধ্যমে অনুমান করা যেত। যেমন এই ধরনের বিজড়িত কণাগুলির "স্পিন"-গুলি যদি বিভিন্ন অভিমুখী অক্ষ (অর্থাৎ শুধু ঊর্ধ্বমুখী বা নিম্নমুখী নয়, বরং এই দুইয়ের মধ্যবর্তী অন্যান্য বিভিন্ন অবস্থাতে) ধরে পরিমাপ করা হয়, তাহলে এভাবে সামষ্টিক জোড়বদ্ধ স্পিনগুলির মধ্যে কিছু সহসম্পর্ক কোয়ান্টাম বলবিজ্ঞানের নিয়মের কারণে অবশ্যই অনেক সবল হবে। অন্যদিকে যদি এগুলি লুক্কায়িত চলরাশিগুলি দ্বারা প্রভাবিত হয়, তাহলে এই সহসম্পর্কগুলি অপেক্ষাকৃত দুর্বল হবে। এ ব্যাপারে বেল একটি গাণিতিক অসমতা প্রদান করেন, যার নাম দেওয়া হয়েছে বেল অসমতা। এটি অনুযায়ী যদি লুক্কায়িত চলরাশি থাকে, তাহলে বৃহৎ সংখ্যক পরিমাপের ফলাফলগুলির মধ্যে সহ-সম্পর্কের মান কখনোই একটি নির্দিষ্ট মানের বেশি হতে পারবে না। কিন্তু কোয়ান্টাম বলবিজ্ঞান ভবিষ্যৎবাণী করে যে কিছু বিশেষ ধরনের পরীক্ষায় বেলের অসমতাটি লংঘিত হবে। যদি বেলের এই চিন্তন পরীক্ষাগুলি ব্যবহারিকভাবে সম্পাদন করা সম্ভব হয়, তাহলে বাস্তবতা যে সবশেষ বিবেচনায় বিশুদ্ধ কোয়ান্টাম বলবৈজ্ঞানিক প্রকৃতির, এ ব্যাপারটি নিশ্চিত করা যাবে, কিংবা এর বিপরীতে ভৌত জটিল বাস্তবতার যে আরও গভীর, আরও মৌলিক স্তরের অস্তিত্ব আছে, সে ব্যাপারটি উন্মোচিত হবে। তবে বেলের প্রস্তাবিত এই পরীক্ষাগুলিতে ("বেলের পরীক্ষাসমূহ") একাধিক সম্ভাব্য ফাঁকফোঁকর ছিল, যার কারণে সেগুলির ফলাফলে বিভ্রান্তির সৃষ্টি হবার সম্ভাবনা রয়ে গিয়েছিল। এরপর বহু দশক ধরে বহুসংখ্যক গবেষক ঐসব ফাঁকফোঁকর বন্ধ করার জন্য কাজ করেন।[২০][১৯]
১৯৬৯ সালে জন ক্লাউজার প্রথম ব্যক্তি হিসেবে একটি ব্যবহারিক "বেলের পরীক্ষা" নকশা করেন। ক্লাউজারের পরীক্ষাটিতে দুইটি ফোটন কণাজোড়কে বিপরীত দিকে উৎক্ষেপণ করার পরে সেগুলির মেরুকরণ নির্ণয় করার মাধ্যমে সেগুলির মধ্যে কোয়ান্টাম বিজড়ন পরিমাপ করতে হয়। ক্লাউজার ১৯৭২ সালে প্রয়াত স্টুয়ার্ট ফ্রিডম্যানের (তৎকালীন স্নাতকোত্তর ছাত্র) সাথে একত্রে এই পরীক্ষাটি সম্পাদন করেন, এবং নিশ্চিত করেন যে ভৌতভাবে বিচ্ছিন্ন হওয়া সত্ত্বেও ফোটনগুলি পরস্পর বিজড়িত থাকার আচরণ প্রদর্শন করেছে। ক্লাউজারের এই পরীক্ষা থেকে আঁচ করা যায় যে আইনষ্টাইনের প্রস্তাবিত লুক্কায়িত চলরাশিগুলি কোয়ান্টাম বিজড়নের প্রভাবগুলি ঠিকমত ব্যাখ্যা করতে পারে না, এবং বাস্তবতাকে মোটামুটি সম্পূর্ণরূপে ব্যাখ্যাকারী একটি তত্ত্ব হিসেবে কোয়ান্টাম তত্ত্ব অটুট রয়েছে।[২০][১৯]
কিন্তু বেলের পরীক্ষায় আরও ফাঁকফোঁকর ছিল। ক্লাউজারের পরীক্ষার প্রায় ১০ বছর পরে ১৯৮০-র দশকে ফরাসি পদার্থবিজ্ঞানী আলাঁ আস্পে ও তাঁর সহযোগীরা ক্লাউজারের পরীক্ষাটিকে আরও পরিশীলিত করেন এবং আরেকটি ফাঁক বন্ধ করেন। তাঁরা ফোটন কণাগুলি উৎস থেকে নিঃসরিত হবার এক সেকেন্ডের একশত কোটিভাগের এক ভাগ সময়ের মধ্যে (কিন্তু শনাক্তকারকের কাছে পৌঁছানোর আগে) সেগুলির অভিমুখ বা দিক পরিবর্তন করার উপায় বের করেন। তাঁরা এ-ও নিশ্চিত করেন যে ফোটন নিঃসরণের সময় যে পরিমাপ ব্যবস্থাগুলি বিদ্যমান ছিল, সেগুলি যেন সর্বশেষ ফলাফলকে প্রভাবিত করতে না পারে। এভাবে লুক্কায়িত চলরাশিগুলির যে কোনও অস্তিত্ব নেই সে ব্যাপারটির উপর জোর দেওয়া হয়। বিজড়িত কণাগুলির পরিমাপের সময় মৌলিকভাবে যা-ই ঘটুক না কেন, আস্পে-র কাজ এটি দেখাতে সক্ষম হয় যে এই ঘটনাটি বিদ্যমান কোয়ান্টাম তত্ত্বের পরিধির ভেতরে থেকেই সংঘটিত হয়। এরপর ২০১৫ সালে চারটি ভিন্ন ভিন্ন গবেষক বেলের পরীক্ষাগুলির শেষ গুরুত্বপূর্ণ ফাঁকটি বন্ধ করেন।[২০][১৯]
অন্যদিকে অস্ট্রীয় পদার্থবিজ্ঞানী আন্টন সাইলিঙার ও তাঁর সহযোগীরা পরিশীলিত সরঞ্জাম ও ধারাবাহিক অনেকগুলি পরীক্ষার মাধ্যমে বিজড়িত কোয়ান্টাম অবস্থাগুলির অধ্যয়ন ও প্রয়োগের ব্যাপক সম্প্রসারণ সাধন করেন। বিশেষ করে তাঁরা ১৯৯৭ সালে (ইতালীয় পদার্থবিজ্ঞানী ফ্রাঞ্চেসকো দে মার্তিনি-র নেতৃত্বে আরেকটি গবেষক দলের সাথে সমসাময়িকভাবে ও স্বাধীনভাবে) কোয়ান্টাম দূর-বহন (কোয়ান্টাম টেলিপোর্টেশন) নামক একটি ঘটনা প্রদর্শন করেন। এই ঘটনাটিতে কোয়ান্টাম বিজড়নকে ব্যবহার করে একটি কণা থেকে যতখুশি দূরত্বে আরেকটি কণাতে কোয়ান্টাম অবস্থা স্থানান্তর করা যায়। সাইলিঙারের গবেষক দল কোয়ান্টাম তথ্যবিজ্ঞান ক্ষেত্রে আরও কয়েকটি অভূতপর্ব কৃতিত্ব অর্জনে সক্ষম হয়। কোয়ান্টাম দূর-বহন প্রক্রিয়াটি ভবিষ্যতে একটি বিশ্বব্যাপী কোয়ান্টাম তথ্য আন্তর্জাল (কোয়ান্টাম ইন্টারনেট) নির্মাণের জন্য যে প্রাথমিক প্রচেষ্টাগুলি হাতে নেওয়া হচ্ছে, সেগুলির কেন্দ্রবিন্দুতে অবস্থিত। সাইলিঙার এই কৌশলটি ব্যবহার করে চীনের মোৎসি মহাকাশযানটি নির্মাণকার্যে সহযোগিতা করেন; ২০১৬ খ্রিস্টাব্দের ইতিহাসের সর্বপ্রথম কোয়ান্টাম যোগাযোগমূলক কৃত্রিম উপগ্রহ হিসেবে এটিকে উৎক্ষেপণ করা হয়।[২০][১৯]
২০২২ খ্রিস্টাব্দে কোয়ান্টাম বিজড়িত ফোটন ব্যবহার করে বাস্তবতার কোয়ান্টাম ভিত্তি নিয়ে গবেষণাকর্মের জন্য ক্লাউজার, আস্পে ও সাইলিঙারকে যৌথভাবে পদার্থবিজ্ঞানে নোবেল পুরস্কার প্রদান করা হয়। এই তিন গবেষক একে অপরের চেয়ে স্বাধীনভাবে কাজ করে কোয়ান্টাম বিজড়ন নামের ঘটনাটির উপর বৈজ্ঞানিক অনুসন্ধানকার্য পরিচালনা করেন ও এটি প্রদর্শনের জন্য নতুন নতুন পরীক্ষার সৃষ্টি করেন। সামষ্টিকভাবে তাদের গবেষণাকর্মগুলি আমাদের কাছে নতুন এক বিশ্বের দ্বার উন্মোচন করেছে এবং আমরা পরিমাপ নিয়ে কীভাবে চিন্তা করি, তার ভিত্তি নড়িয়ে দিয়েছে। একই সাথে তাদের গবেষণাকর্মগুলি কোয়ান্টাম তথ্যবিজ্ঞান ক্ষেত্রটিতে ব্যাপক অবদান রেখেছে। কোয়ান্টাম তথ্যবিজ্ঞান হল সেই বৈজ্ঞানিক ক্ষেত্র যেখানে পরিগণন (কম্পিউটিং), যোগাযোগ ও তথ্যগুপ্তিবিদ্যা বা গুপ্তলিখনবিদ্যা (ক্রিপ্টোগ্রাফি) ক্ষেত্রগুলিতে নাটকীয় অগ্রগতি অর্জনের উদ্দেশ্যে কোয়ান্টামীয় মূলনীতিগুলিকে ব্যবহার করে ব্যবহারিক যন্ত্রপাতি ও কৌশল সৃষ্টির প্রতিযোগিতা চলমান আছে। আস্পে, ক্লাউজার ও সাইলিঙারের গবেষণাকর্মগুলি ব্যবহারিক ক্ষেত্রে প্রয়োগযোগ্য এমন সব তাত্ত্বিক পদ্ধতি ও এমন সব নিষ্পত্তিকারী পরীক্ষাভিত্তিক পরিমাপ প্রদান করেছে, যেগুলি চিরায়ত বিশ্ব ও কোয়ান্টাম বিশ্বের মধ্যে বিদ্যমান পার্থক্যকে আরও সুস্পষ্ট করেছে। এগুলি দেখিয়েছে যে কোয়ান্টাম বস্তুগুলি বিজড়নের মাধ্যমে এমন উপায়ে একে অপরের সম্পর্কিত যে ব্যাপারটি চিরায়ত বস্তুতে অসম্ভব। তাদের কাজ কোয়ান্টাম পরিগণন ও কোয়ান্টাম যোগাযোগের মৌলিক ভিত্তি গঠন করেছে।[২০]
সহজ ভাষায় ব্যাখ্যা
[সম্পাদনা]ধরুন, আপনার ও আপনার বন্ধুর কাছে একটি বাক্স আছে, যাতে দুটো হাতমোজা আছে। হাত মোজার একটি বৈশিষ্ট্য হলো, এক হাতের হাতমোজা অন্য হাতে পড়া যায় না। একটা হাতমোজা ডান হাতের ও অন্যটা বাম হাতের। এখন, আপনি ও আপনার বন্ধু দৈবচয়ন পদ্ধতিতে চোখ বন্ধ করে দুটি হাত মোজা নিলেন ও একটি বিমানে উঠে একজন ব্রিটেনে ও অন্যজন কাতারে চলে আসলেন। উল্লেখ্য, আপনারা কেউই আপনাদের হাতমোজা খুলে দেখেননি।
এখন আপনি যদি ব্রিটেনে আপনার হাতমোজা বের করে দেখেন যে সেটা বাম হাতের হাতমোজা, তাহলেই আপনি জেনে যাবেন যে আপনার বন্ধুর কাছে যে মোজাটা রয়েছে সেটা ডান হাতের মোজা। সে পকেট থেকে বের করার আগেই আপনি নিশ্চিতভাবে জানতে পারবেন তার মোজার তথ্য।
এখানে আমরা বলতে পারি যে হাতমোজা দুইটি বিজড়িত (এনট্যাঙ্গল্ড) হয়ে ছিল। তাই একটা সম্পর্কে জানা মাত্রই অপরটি সম্পর্কে জানা হয়ে গেছে।
তথ্যসূত্র
[সম্পাদনা]- ↑
Einstein A, Podolsky B, Rosen N; Podolsky; Rosen (১৯৩৫)। "Can Quantum-Mechanical Description of Physical Reality Be Considered Complete?"। Phys. Rev.। 47 (10): 777–780। ডিওআই:10.1103/PhysRev.47.777
 । বিবকোড:1935PhRv...47..777E।
। বিবকোড:1935PhRv...47..777E।
- ↑ Schrödinger E (১৯৩৫)। "Discussion of probability relations between separated systems"। Mathematical Proceedings of the Cambridge Philosophical Society। 31 (4): 555–563। এসটুসিআইডি 121278681। ডিওআই:10.1017/S0305004100013554। বিবকোড:1935PCPS...31..555S।
- ↑ Schrödinger E. (১৯৩৬)। "Probability relations between separated systems"। Mathematical Proceedings of the Cambridge Philosophical Society। 32 (3): 446–452। এসটুসিআইডি 122822435। ডিওআই:10.1017/S0305004100019137। বিবকোড:1936PCPS...32..446S।
- ↑ উত্তর আইরীয় পদার্থবিজ্ঞানী জন বেল depicts the Einstein camp in this debate in his article entitled "Bertlmann's socks and the nature of reality", p. 143 of Speakable and unspeakable in quantum mechanics: "For EPR that would be an unthinkable 'spooky action at a distance'. To avoid such action at a distance they have to attribute, to the space-time regions in question, real properties in advance of observation, correlated properties, which predetermine the outcomes of these particular observations. Since these real properties, fixed in advance of observation, are not contained in quantum formalism, that formalism for EPR is incomplete. It may be correct, as far as it goes, but the usual quantum formalism cannot be the whole story." And again on p. 144 Bell says: "Einstein had no difficulty accepting that affairs in different places could be correlated. What he could not accept was that an intervention at one place could influence, immediately, affairs at the other." Downloaded 5 July 2011 from Bell, J. S. (১৯৮৭)। Speakable and Unspeakable in Quantum Mechanics (পিডিএফ)। CERN। আইএসবিএন 0521334950। ১২ এপ্রিল ২০১৫ তারিখে মূল (পিডিএফ) থেকে আর্কাইভ করা। সংগ্রহের তারিখ ১৪ জুন ২০১৪।
- ↑ ক খ Yin, Juan; Cao, Yuan; Yong, Hai-Lin; Ren, Ji-Gang; Liang, Hao; Liao, Sheng-Kai; Zhou, Fei; Liu, Chang; Wu, Yu-Ping; Pan, Ge-Sheng; Li, Li; Liu, Nai-Le; Zhang, Qiang; Peng, Cheng-Zhi; Pan, Jian-Wei (২০১৩)। "Bounding the speed of 'spooky action at a distance"। Physical Review Letters। 110 (26): 260407। arXiv:1303.0614
 । এসটুসিআইডি 119293698। ডিওআই:10.1103/PhysRevLett.110.260407। পিএমআইডি 23848853। বিবকোড:2013PhRvL.110z0407Y।
। এসটুসিআইডি 119293698। ডিওআই:10.1103/PhysRevLett.110.260407। পিএমআইডি 23848853। বিবকোড:2013PhRvL.110z0407Y।
- ↑ ক খ Matson, John (১৩ আগস্ট ২০১২)। "Quantum teleportation achieved over record distances"। Nature News। এসটুসিআইডি 124852641। ডিওআই:10.1038/nature.2012.11163।
- ↑ ক খ Francis, Matthew. Quantum entanglement shows that reality can't be local, Ars Technica, 30 October 2012
- ↑ Roger Penrose, The Road to Reality: A Complete Guide to the Laws of the Universe, London, 2004, p. 603.
- ↑ Griffiths, David J. (২০০৪), Introduction to Quantum Mechanics (2nd ed.), Prentice Hall, আইএসবিএন 978-0-13-111892-8
- ↑ Kocher, CA; Commins, ED (১৯৬৭)। "Polarization Correlation of Photons Emitted in an Atomic Cascade"। Physical Review Letters। 18 (15): 575–577। ডিওআই:10.1103/PhysRevLett.18.575। বিবকোড:1967PhRvL..18..575K।
- ↑ Carl A. Kocher, Ph.D. Thesis (University of California at Berkeley, 1967). Polarization Correlation of Photons Emitted in an Atomic Cascade
- ↑ J. A. Formaggio, D. I. Kaiser, M. M. Murskyj, and T. E. Weiss (2016), "Violation of the Leggett-Garg inequality in neutrino oscillations". Phys. Rev. Lett. Accepted 23 June 2016.
- ↑ Hensen, B.; ও অন্যান্য (২১ অক্টোবর ২০১৫)। "Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres"। Nature। 526 (7575): 682–686। arXiv:1508.05949
 । hdl:2117/79298। এসটুসিআইডি 205246446। ডিওআই:10.1038/nature15759। পিএমআইডি 26503041। বিবকোড:2015Natur.526..682H। See also free online access version.
। hdl:2117/79298। এসটুসিআইডি 205246446। ডিওআই:10.1038/nature15759। পিএমআইডি 26503041। বিবকোড:2015Natur.526..682H। See also free online access version.
- ↑ Markoff, Jack (২১ অক্টোবর ২০১৫)। "Sorry, Einstein. Quantum Study Suggests 'Spooky Action' Is Real."। The New York Times। সংগ্রহের তারিখ ২১ অক্টোবর ২০১৫।
- ↑ Arndt, M; Nairz, O; Vos-Andreae, J; Keller, C; van der Zouw, G; Zeilinger, A (১৪ অক্টোবর ১৯৯৯)। "Wave–particle duality of C60 molecules"। Nature। 401 (6754): 680–682। এসটুসিআইডি 4424892। ডিওআই:10.1038/44348। পিএমআইডি 18494170। বিবকোড:1999Natur.401..680A। (সদস্যতা প্রয়োজনীয়)
- ↑ Olaf Nairz, Markus Arndt, and Anton Zeilinger, "Quantum interference experiments with large molecules", American Journal of Physics, 71 (April 2003) 319–325.
- ↑ Lee, K. C.; Sprague, M. R.; Sussman, B. J.; Nunn, J.; Langford, N. K.; Jin, X.- M.; Champion, T.; Michelberger, P.; Reim, K. F.; England, D.; Jaksch, D.; Walmsley, I. A. (২ ডিসেম্বর ২০১১)। "Entangling macroscopic diamonds at room temperature"। Science। 334 (6060): 1253–1256। এসটুসিআইডি 206536690। ডিওআই:10.1126/science.1211914। পিএমআইডি 22144620। বিবকোড:2011Sci...334.1253L।
- ↑ sciencemag.org, supplementary materials
- ↑ ক খ গ ঘ ঙ "Press release: The Nobel Prize in Physics 2022"। অজানা প্যারামিটার
|site=উপেক্ষা করা হয়েছে (সাহায্য) - ↑ ক খ গ ঘ ঙ চ ছ Lee Billings (৪ অক্টোবর ২০২২)। "Explorers of Quantum Entanglement Win 2022 Nobel Prize in Physics"। Scientific American। সংগ্রহের তারিখ ৫ অক্টোবর ২০২২।

