বৃত্ত

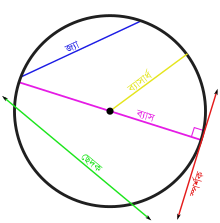একটি নমুনা বৃত্ত

ইউক্লিডিয় জ্যামিতিতে, একটি নির্দিষ্ট বিন্দু (কেন্দ্র) থেকে একটি নির্দিষ্ট দূরত্বে (ব্যাসার্ধ) একই সমতলে অবস্থিত সমস্ত বিন্দুর সেটকে বৃত্ত বলা হয়।

বৃত্তের উপর অবস্থিত যেকোন দুটি বিন্দুর সংযোগকারী সরলরেখাংশকে বলা হয় জ্যা । বৃত্তের কেন্দ্রগামী যেকোন জ্যাকে বলা হয় তার ব্যাস । বৃত্তের ব্যাস হ্ল তার দীর্ঘতম জ্যা । ব্যাসের দৈর্ঘ্য ব্যাসার্ধের দ্বিগুন হয় ।

বৃত্ত একটি আবদ্ধ বক্ররেখা বিধায় যেকোন বৃত্ত স্থানকে অন্তস্থঃ এবং বহিস্থঃ - এই দুইভাগে ভাগ করে । এদের মধ্যে অন্তস্থঃ অঞ্চলটি সসীম এবং বহিস্থঃ অংশটি অসীম। অন্তস্থ অঞ্চলটি চাকতি বা disk হিসেবেও পরিচিত ।

বৃত্তের সীমানাকে বলা হয় পরিধি এবং পরিধির অংশকে বলা হয় বৃত্তচাপ ।

বৃত্ত একটি বিশেষ ধরনের উপবৃত্ত যার উপকেন্দ্রদ্বয় সমবিন্দু । একটি বৃত্তীয় কনিকের অক্ষের সাপেক্ষে লম্ব সমতল কনিকটিকে ছেদ করলে প্রাপ্ত বক্ররেখাটি একটি বৃত্ত হয় ।

বিশ্লেষণী ফলাফল সমূহ

বৃত্তের ব্যাসার্ধ r=1, কেন্দ্র (a, b)=(1.2, -0.5)।

জ্যা, অভিলম্ব, স্পর্শক এবং ব্যাস ।

x-y কার্তেসীয় স্থানাঙ্ক ব্যাবস্থায়, (a, b) কেন্দ্র এবং r ব্যাসার্ধ বিশিষ্ট বৃত্তের সমীকরণ হল :

$\left( x - a \right)^2 + \left( y - b \right)^2=r^2.$

বৃত্তস্থঃ যেকোন বিন্দুর উপর পিথাগোরাসের উপপাদ্য প্রয়োগ করে বৃত্তের এই সমীকরণটি পাওয়া যায় । মূলবিন্দুতে কেন্দ্র হলে সমীকরণটি দাঁড়ায় :

$x^2 + y^2 = r^2. \!\$

পরামিতিক সমীকরণে রূপান্তর করা হলে :

$x = a+r\,\cos t,\,\!$

$y = b+r\,\sin t\,\!$

পাই (π)

পাই (π) হল বৃত্তের পরিধি এবং ব্যাসের অনুপাত, যা একটি ধ্রূবক। পাই অত্যন্ত বিখ্যাত একটি ধ্রুবক। গণিতবিদদের মতে পাই হল বিশ্বের সবচেয়ে সুন্দর সংখ্যা। এটি একটি তুরীয় ( ট্রান্সেডেন্টাল) সংখ্যা।

ক্ষেত্রফল

Area of the circle = π × area of the shaded square

বৃত্তের ভেতরে চাকতি আকারের অঞ্চলটির ক্ষেত্রফল $\pi$ এবং তার ব্যাসার্ধের বর্গের গুনফলের সমান ।

$Area = \pi \cdot r^2$

ইতিহাস

লিখিত ইতিহাস সংরক্ষণ শুরু হওয়ারও আগে থেকে বৃত্ত সম্পর্কে মানুষের ধারণা ছিল । চাকা, যা মানব সভ্যতার অগ্রগতীতে ব্যাপক অবদান রেখেছে, বৃত্তাকার । চাকার সাথে সম্পর্কিত আরো কিছু আবিষ্কার যেমন গিয়ার প্রভৃতিও বৃত্তাকার । গণিতে বৃত্তের অধ্যয়ন পরবর্তীতে জ্যামিতি ও ক্যালকুলাসের মত উচ্চতর শাখা গুলোর উন্নয়নে অবদান রেখেছে । বৃত্তের ইতিহাসে কয়েকটি গুরূত্বপূর্ণ ঘটনা হল :

• ১৭০০ খ্রী,পূ - রাইন্ড প্যাপিরাসে বৃত্তের ক্ষেত্রফল নির্নয়ের একটি পদ্ধতি লিপিবদ্ধ হয় । এতে ২৫৬/৮১ কে π এর মান ধরা হয় ।
• ৩০০ খ্রী,পূ - ইউক্লিডের এলিমেন্টস এর তৃতীয় গ্রন্থে বৃত্তের বৈশিষ্ট্য সমূহ নিয়ে বিস্তারিত আলোচনা করা হয় ।
• ১৮৮০ - লিন্ডেমান প্রমান করেন যে π একটি transcendental সংখ্যা । এর ফলে হাজার বছর ধরে চলে আসা বৃত্তকে বর্গ রূপান্তরের সমস্যাটির সুরাহা ঘটে ।

বৈশিষ্ট্য

• বৃত্ত হল নির্দিষ্ট পরিসীমার মধ্যে আবদ্ধ বৃহত্তম ক্ষেত্রফল ।
• বৃত্ত বিশেষ ধরনের প্রতিসাম্যের অধিকারী একটি আকৃতি । কেন্দ্রগামী যেকোন রেখাই প্রতিফলন প্রতিসম অক্ষ হিসেবে কাজ করে এবং কেন্দ্রের সাপেক্ষে যেকোন কোনে ঘূর্নণ প্রতিসাম্য তৈরি হয় ।
• প্রতিটি বৃত্তের আকৃতি অভিন্ন ।
  • বৃত্তের পরিধি ও ব্যাসের অনুপাত একটি ধ্রূব সংখ্যা, একে π দ্বারা প্রকাশ করা হয় ।
• কার্তেসীয় স্থানাঙ্ক ব্যাবস্থায় মূলবিন্দুতে কেন্দ্র বিশিষ্ট একক ব্যাসার্ধের বৃত্তকে বলা হয় একক বৃত্ত ।
• যেকোন তিনটি বিন্দুগামী, যারা অসমরেখ, একটি এবং কেবলমাত্র একটি বৃত্ত রয়েছে ।