পারমাণবিক বল

রেইড বিভব (১৯৬৮) অনুযায়ী দূরত্বের ফাংশন হিসেবে দুটি নিউক্লিয়নের মধ্যস্থ বল (10,000 N এককে)।^[১] নিউট্রন এবং প্রোটনের স্পিন সদৃশ এবং তারা S কৌণিক ভরবেগ অবস্থায় রয়েছে। কণাসমূহের মধ্যে আকর্ষক (ঋণাত্বক) বল ১ fm দূরত্বে সর্বোচ্চ মান ~২৫,০০০ N লাভ করে। ০.৮ fm এর চেয়ে খুব নিকটস্থ কণাসমূহ বৃহৎ বিকর্ষক (ধণাত্বক) বল অনুভব করে। ১ fm এর বেশি দূরত্বে থাকা কণাগুলোও আকর্ষণ অনুভব করে (ইউকাওয়া বিভব), তবে সে বল দূরত্বের ঘাতীয় ফাংশন হিসেবে পতনশীল।

রেইড বিভব (১৯৬৮) অনুযায়ী দূরত্বের ফাংশন হিসেবে অনুরূপ দুটি নিউক্লিয়নের মধ্যস্থ বিভবশক্তি (MeV এককে)। বিভব খাত ০.৮ fm দূরত্বে সর্বনিম্ন। এই বিভব দ্বারা নিউক্লিয়নগুলো ঋনাত্বক "যোজন শক্তি" দ্বারা যুক্ত হয়ে যেতে পারে।

পারমাণবিক বল বা নিউক্লীয় বল (অথবা নিউক্লিয়ন–নিউক্লিয়ন মিথষ্ক্রিয়া) হল পরমাণুতে প্রোটন ও নিউট্রনের মধ্যে ক্রিয়াশীল বল। নিউট্রন এবং প্রোটন উভয়েই নিউক্লিয়ন, এবং নিউক্লীয় বল দ্বারা প্রায় একইভাবে প্রভাবিত হয়। প্রোটনের +1 e চার্জ থাকার দরুণ একটি বিকর্ষক বৈদ্যুতিক বল অনুভব করে, কিন্তু নিকটদূরত্বে নিউক্লীয় বল এই বিকর্ষণ বলের চেয়ে বেশি প্রভাবশীল। পারমাণবিক বলের কারণেই প্রোটন ও নিউট্রন একত্রিত হয়ে পরমাণুর নিউক্লিয়াস গঠন করে।

~১ ফেমটোমিটার (fm, বা ১.০ × ১০^−১৫ মিটার) দূরত্বে নিউক্লিয়নসমূহের মধ্যে পারমাণবিক বল প্রচণ্ড আকর্ষণ উৎপন্ন করে, কিন্তু ~২.৫fm এর বেশি দূরত্বে খুব দ্রুত এর প্রাবল্যের পতন ঘটে এবং লক্ষণীয় প্রভাব হারিয়ে যায়। অন্যদিকে, ০.৭ fm এর কম দূরত্বে পারমাণবিক বল বিকর্ষক হয়ে যায়। এই বিকর্ষক বৈশিষ্ট্য নিউক্লিয়াসের আকারের নিম্নসীমার জন্য দায়ী, কেননা নিউক্লিয়নগুলো এই বল অতিক্রম করে আরও কাছাকাছি আসতে পারে না। তুলনামূলকভাবে, পরমাণুর আকার, এই দূরত্বের তুলনায় পাঁচ ঘাত বেশি। পারমাণবিক বল কোন সরল বল নয়, কারণ এটি নিউক্লিয়নের স্পিন এর ওপর নির্ভর করে, এর স্থিতিস্থাপক বৈশিষ্ট্য আছে, এবং নিউক্লিয়নের আপেক্ষিক ভরবেগের সথেও সম্পর্কিত হতে পারে।^[২] পারমাণবিক বল, পাঁচটি মৌলিক বলের অন্তর্গত।

পারমাণবিক শক্তি কেন্দ্রে এবং পারমাণবিক অস্ত্রে ব্যবহৃত শক্তির উৎস হিসেবে নিউক্লীয় বলের গুরুত্বপূর্ণ ভূমিকা রয়েছে। চার্জযুক্ত প্রোটনসমূহের তড়িৎ বিকর্ষণ পরাভূত করে তাদের একত্রে আবদ্ধ করার জন্য কাজ (শক্তি) প্রয়োগ করতে হয়। পারমাণবিক বল দ্বারা প্রোটন-নিউট্রনের সমন্বয়ে নিউক্লিয়াস গঠনকালে সেই শক্তি সঞ্চিত হয়। পরমাণুর নিউক্লিয়াসের ভর, এর অন্তস্থ নিউক্লিয়নগুলোর মোট ভরের চেয়ে কম হয়। ভরের এই পার্থক্য হচ্ছে ভর ত্রুটি, যা কাঠামোটিতে প্রযুক্ত শক্তির সমতুল্য হিসেবে দেখানো যায়। একটি নিউক্লিয়াস ভেঙে নিউক্লিয়নে ফিরে যাবার সময় নিউক্লীয় যোজন শক্তি নির্গত হয়। এটি হচ্ছে এক ধরনের তড়িৎচুম্বকীয় বিভব শক্তি, যা চার্জযুক্ত নিউক্লীয় কণার ওপর পারমাণবিক বলের প্রভাব বিলুপ্ত হওয়ার সময় নির্গত হয়।^[৩]^[৪]

নিউক্লীয় বলের পরিমাপ, আংশিকভাবে পরীক্ষালদ্ধ কিছু সমীকরণের ওপর নির্ভরশীল। এই সমীকরণগুলো নিউক্লিয়নসমূহের মধ্যস্থ বিভব শক্তির ব্যাখ্যা করে। (সাধারণত কণা পর্যায়ের কাঠামোকে বিভব শক্তি দ্বারা সরলভাবে বর্ণনা করা যায়; বিভবের ঋণাত্বক নতি ভেক্টর বলের সমান।) এসব সমীরকণের ধ্রুবক রাশিগুলোর মানও পরীক্ষালদ্ধ। নিউক্লিয়ন-নিউক্লিয়ন মিথষ্ক্রিয়ার বৈশিষ্ট্য বর্ণনার প্রচেষ্টায় এই বিভব কাজে আসে। মান নির্ণয়ের পর এসব কণা বিভবকে বিভিন্ন সমীকরণে প্রয়োগ করা যায়, যেমন শ্রোডিঙার সমীকরণ দ্বারা নিউক্লিয়ন কাঠামোর কোয়ান্টাম বৈশিষ্ট্য নির্ধারণের ক্ষেত্রে।

১৯৩২ সালে নিউট্রন আবিষ্কার এর পর জানা যায়, পারমাণবিক নিউক্লিয়াস প্রোটন ও নিউট্রন মিলে তৈরি, যারা একটি আকর্ষক বল দ্বারা সংযুক্ত থাকে। ১৯৩৫ সালের মধ্যে নিউক্লীয় বলের ধারণাটি স্বীকৃতি পেয়ে গিয়েছিল, এবং বলটি মেসন কণা দ্বারা প্রবাহিত বলে কল্পনা করা হত। এই তাত্ত্বিক ধারণায় ইউকাওয়া বিভবের সংজ্ঞা অন্তর্ভুক্ত ছিল, যা প্রথমদিককার একটি নিউক্লীয় বিভবের উদাহরণ। ১৯৪৭ সালে একটি পরীক্ষায় মেসন কণা আবিষ্কৃত হয়। ১৯৭০ এর মধ্যে কোয়ার্ক কাঠামো তত্ত্ব বিকশিত হয়, যেখানে মেসন এবং নিউক্লিয়ন কণাগুলো কোয়ার্ক এবং গ্লুয়ন দ্বারা গঠিত বলে ব্যাখ্যা করা হয়। এই কাঠামো অনুযায়ী, পাশাপাশি অবস্থিত নিউক্লিয়নের মধ্যে মেসন বিনিময় থেকে নিউক্লীয় বলের উদ্ভব ঘটে, এবং বলটি মূলত সবল নিউক্লীয় বলের অবশিষ্টাংশ বলে প্রতীয়মান হয়।

বর্ণনা[সম্পাদনা]

নিউক্লীয় বল সাধারণত নিউক্লিয়নের সংশ্লিষ্ট বলে গণিত হলেও এটি মূলত হ্যাড্রন বা কোয়ার্ক-গঠিত কণাসমূহের মধ্যে কাজ করে। কণাসমূহ ~ ০.৭ fm এর চেয়ে নিকটাবস্থায় এলে (স্পিন সাপেক্ষে) বলটি বিকর্ষক হয়ে ওঠে, যা নিউক্লিয়নসমূহের মধ্যে একটি গড়পড়তা নূন্যতম দূরত্ব বজায় রাখে। এই বিকর্ষক বৈশিষ্ট্যটি সমরূপ নিউক্লিয়নসমূহের মধ্যে পাউলির অপবর্জন নীতি থেকে উদ্ভূত। ভিন্ন জাতীয় দুটি নিউক্লিয়নের অন্তর্গত সমরূপ কোয়ার্কসমূহের মধ্যেও পাউলি অপবর্জন কার্যকর হতে পারে।

ক্ষেত্র প্রাবল্য[সম্পাদনা]

০.৭ fm এর বেশি দূরত্বে নিউক্লীয় বল আকর্ষক বৈশিষ্ট্য অর্জন করে, এবং নিউক্লিয়নসমূহের মধ্যে ০.৯ fm দূরত্বে সর্বোচ্চ শক্তি প্রদর্শন করে। তবে এর বেশি দূরত্বে বলটি দ্রুত কমতে থাকে এবং ২.০ fm দূরত্বে একদমই নগণ্য হয়ে যায়। প্রসঙ্গত, নিউক্লিয়নের ব্যাসার্ধ সাধারণত ০.৮ fm হয়।^[৫]

নিকট দূরত্বে (~ <১.৭ fm) পারমাণবিক বলের আকর্ষণ শক্তি কুলম্ব বিকর্ষণের চেয়ে প্রবল হয়, ফলে নিউক্লিয়াসে প্রোটনসমূহের মধ্যকার বিকর্ষণকে অতিক্রম করে তাদের সংঘবদ্ধ করতে পারে। তবে কুলম্ব বিকর্ষণের প্রভাব বেশি দূরত্বে বিস্তৃত, তাই ২ থেকে ২.৫ fm দূরত্বে এটিই প্রোটনগুলোর মধ্যে প্রধান কার্যকর বলে পরিণত হয়।

নিউক্লীয় বলের একটি স্পিন-নির্ভর অনুষঙ্গ রয়েছে। সমন্বিত স্পিনের নিউক্লিয়নগুলোর মধ্যে বলটি প্রবলতর। একই জাতীয় দুটি কণার মধ্যে বলটির শক্তি তাদের আবদ্ধ করার মত যথেষ্ট শক্তিশালী নয়, কেননা পরস্পরের নিকটস্থ বা একই কোয়ান্টাম দশাস্থিত দুটি সমরূপ কণার স্পিন ভেক্টর অবশ্যই বিপরীতমুখী হতে হয়। ফার্মিয়নের এই প্রয়োজনীয়তা পাউলি অপবর্জন নীতি হতে উদ্ভূত। ভিন্নধর্মী ফার্মিয়ন কণা (যেমন একটি নিউট্রন ও একটি প্রোটন) পরস্পরের নিটকবর্তী হলেও স্পিন সমন্বিত রাখতে পারে এবং এক্ষেত্রে পাউলির নীতি ভঙ্গ হয় না, এবং নিউক্লীয় বল কণাগুলোকে সংঘবদ্ধ করতে পারে কারণ ভিন্ন স্পিনের কণাযুগলের মধ্যে বলটির প্রাবল্য বেশি।

নিউক্লীয় বলের একটি স্থিতিস্থাপক বৈশিষ্ট্যও রয়েছে যা নিউক্লিয়নের স্পিন ও কৌণিক ভরবেগের ওপর নির্ভর করে, এবং এর ফলে নিউক্লিয়াসের আদর্শ গোলাকার কাঠামোয় বিকৃতি হয়।

নিউক্লীয় যোজন[সম্পাদনা]

একটি নিউক্লিয়াসকে অযুগ্ন প্রোটন ও নিউট্রনে বিভক্ত করতে হলে পারমাণবিক বলের বিরুদ্ধে কাজ করতে হয়। আবার বিপরীতভাবে, একাধিক নিউক্লিয়ন বা নিউক্লিয়াস থেকে একটি নিউক্লিয়াস গঠনের সময় নিউক্লীয় যোজন শক্তি নির্গত হয়। ভর-শক্তি সমতা (তথা E = mc²) সূত্র অনুসারে, ওই শক্তি নির্গমনের ফলে নিউক্লিয়াসের ভর তার সদস্য নিউক্লিয়নগুলোর মোট ভরের তুলনায় কম হয়, এবং তথাকথিত "ভর ত্রুটি" পরিলক্ষিত হয়।^[৬]

পারমাণবিক বল নিউট্রন ও প্রোটনের সাপেক্ষে প্রায় অপরিবর্তিত থাকে। এই বৈশিষ্ট্য হল চার্জ স্বাধীনতা। এই বল নিউক্লিয়নসমূহের স্পিনের ওপর নির্ভর করে, কারণ এর একটি বিকেন্দ্রিক বা স্থিতিস্থাপক অনুষঙ্গ রয়েছে। বলের এই অংশটি চক্রীয় কৌণিক ভরবেগ সংরক্ষণ করে না (যা কেন্দ্রীয় শক্তি দ্বারা সংরক্ষিত হয়ে থাকে)।

ওয়ার্নার হাইজেনবার্গের প্রস্তাবনা অনুসারে, যে প্রতিসাম্য থেকে সবল শক্তির জন্ম হয় তা হল: প্রোটন এবং নিউট্রন কেবল চার্জ ব্যতীত অন্য সব দিক দিয়ে অভিন্ন (যদিও এই সমতা নিখুঁত নয়, কারণ নিউট্রনসমূহ প্রোটনের তুলনায় অতি সামান্য ভারী হয়)। তাই প্রোটন এবং নিউট্রনকে একই কণা হিসেবে দেখা হয়, যাদের আইসোস্পিন কোয়ান্টাম সংখ্য ভিন্ন; গতানুগতিকভাবে, প্রোটেনের আইসোস্পিন আপ এবং নিউট্রনের আইসোস্পিন ডাউন। SU(2) আইসোস্পিন রূপান্তরের অধীনে, কণাসমূহের অন্যান্য মিথষ্ক্রিয়ার মত সবল মিথষ্ক্রিয়াও অপরিবর্তনশীল থাকে। পরস্পর-ক্রিয়াশীল কণাগুলোর মোট আইসোস্পিনের মান ০ হলেই কেবল সবল আকর্ষণ উপস্থিত থাকে, যা পরীক্ষা দ্বারা সমর্থিত।^[৭]

হালকা নিউক্লিয়াসের যোজন শক্তির পর্যবেক্ষণ এবং বিক্ষেপণ পরীক্ষাই হল পারমাণবিক বল সম্পর্কে বর্তমানে প্রাপ্ত ধারণার উৎস।

পারমাণবিক বলের উদ্ভব ঘটে নিউক্লিয়নসমূহের মধ্যে কাল্পনিক (ভার্চুয়াল) লঘু মেসন কণার হস্তান্তর থেকে, যেমন কাল্পনিক পাইয়ন, এবং স্পিনসম্পন্ন রো এবং ওমেগা ভেক্টর মেসন। এই "কাল্পনিক মেসন" কাঠামোতে ভেক্টর মেসনগুলোই নিউক্লীয় বলের স্পিন-নির্ভরতার কারণ।

পারমাণবিক বা নিউক্লীয় বল, পূর্বপ্রচলিত দুর্বল মিথষ্ক্রিয়া বা দুর্বল নিউক্লীয় বল হতে ভিন্ন। দূর্বল মিথষ্ক্রিয়া চারটি মৌলিক মিথষ্ক্রিয়ার মধ্যে একটি, এবং বিটা ক্ষয় এর মত প্রক্রিয়ায় ভূমিকা রাখে। দূর্বল নিউক্লীয় বল নিউক্লিয়নের পারস্পরিক ক্রিয়ায় ভূমিকা রাখে না, তবে এটি নিউট্রন থেকে প্রোটন এবং বিপরীতমুখী রূপান্তরের জন্য দায়ী।

ইতিহাস[সম্পাদনা]

জেমস চ্যাডউইক ১৯৩২ সালে নিউট্রন আবিষ্কারের মধ্য দিয়ে পারমাণবিক বিজ্ঞানের সূচনা করেন, এবং সূচনাকাল থেকেই এই ক্ষেত্রের কেন্দ্রে রয়েছে পারমাণবিক বল। নিউক্লিয়নসমূহের মধ্যস্থ ক্রিয়া-প্রতিক্রিয়া বা নিউক্লিয়ন-নিউক্লিয়ন বল (NN forces) দ্বারা পদার্থের পরমাণুর সামগ্রিক বৈশিষ্ট্যের ব্যাখ্যা করাই হল নিউক্লীয় বিজ্ঞানীদের চিরাচরিত লক্ষ্য।

নিউট্রন আবিষ্কারের কয়েকমাস পরেই ওয়ার্নার হাইজেনবার্গ^[৮]^[৯]^[১০] এবং দিমিত্রি ইভানেনকো^[১১] প্রোটন-নিউট্রন ভিত্তিক নিউক্লিয়াসের কাঠামোর প্রস্তাব করেন।^[১২] হাইজেনবার্গ এজন্য কোয়ান্টাম তত্ত্বের আশ্রয় নিয়েছিলেন, যা ছিল সে সময়ের সাপেক্ষে একটি অসাধারণ পন্থা, এবং নিউক্লিয়াসকে একটি কোয়ান্টাম কাঠামো হিসেবে ব্যাখ্যায় অসামান্য অগ্রগতি এনেছিল।^[১৩] নিউক্লিয়নসমূহের বন্ধনে নিউক্লীয় বিনিময় শক্তির ধারণাটিও হাইজেনবার্গই প্রথম উত্থাপন করেন। তিনি প্রোটন এবং নিউট্রনকে একই কণার ভিন্ন কোয়ান্টাম দশা হিসেবে দেখতেন, যাদের পার্থক্য কেবল কেবল আইসোস্পিন কোয়ান্টাম সংখ্যায়।

নিউক্লিয়াস কাঠামোর প্রারম্ভিক আর একটি তত্ত্ব ছিল ১৯৩০ দশকের তরল বিন্দু কাঠামো। সকল স্থিতিশীল নিউক্লিয়াসে প্রতিটি নিউক্লিয়নের গড় বন্ধন শক্তি, একটি জলবিন্দুর পরমাণুসমূহের মতই প্রায় সমান। তরল বিন্দু কাঠামোতে নিউক্লয়িাসকে এক ফোঁটা অসংকোচনীয় পারমাণবিক তরল হিসেবে গণ্য করা হয়, যেখানে নিউক্লিয়নগুলো তরলের পরমাণুর ভূমিকা নেয়। এই কাঠামোটি সর্বপ্রথম প্রস্তাব করেছিলেন জর্জ গ্যামফ, এবং পরে এর উন্নতি সাধন করেছেন নিলস বোর, হাইজেনবার্গ, এবং কার্ল ফ্রিডরিখ ফন ভাইৎস্যেকার। এই কাঠামোটি নিউক্লিয়াসের সমস্ত বৈশিষ্ট্যের ব্যাখ্যা দিতে না পারলেও গোলাকার কাঠামোটি ব্যাখ্যা করতে সক্ষম হয়েছিল, এবং নিউক্লিয় বন্ধন শক্তিরও একটি ভাল ধারণা দিতে পেরেছিল।

পারমাণবিক শক্তির বর্ণনার প্রথম প্রয়াস এসেছিল ১৯৩৪ সালে হিদেকি ইউকাওয়ার গবেষণায়। তার তত্ত্ব অনুসারে নিউক্লিয়নসমূহের মিথষ্ক্রিয়ার মধ্যস্থতা করে বৃহৎ ভরের বোসন (মেসন) কণা। কোয়ান্টাম ক্রোমোডায়নামিক্স (QCD) মেসন তত্ত্বের মৌলিকত্ব বিলুপ্ত হলেও এই মেসন-বিনিময় কাঠামোটিই এখন পর্যন্ত NN বিভব গণনার সবচেয়ে কার্যকর উপায়। ইউকাওয়া বিভব (বা পরীক্ষিত কুলম্ব বিভব) হল নিম্নরূপ:

V_{\text{Yukawa}}(r)=-g^{2}{\frac {e^{-\mu r}}{r}},

এখানে g হল বিভবের বিস্তার, $\mu$ ইউকাওয়া কণা ভর, এবং r কণাটির ব্যাসার্ধীয় দূরত্ব। বিভবটি মোনোটোন হারে বর্ধিষ্ণু, যা ইঙ্গিত করে যে বলটি সবসময়ই আকর্ষক। ধ্রুবকগুলোর মান পরীক্ষালদ্ধ। ইউকাওয়া বিভবটি কেবল কণাসমূহের দূরত্বের ওপর নির্ভর করে, তাই এটি নিউক্লীয় শক্তিকে একটি কেন্দ্রীয় শক্তি হিসেবে গণনা করে।

১৯৩০ দশক জুড়ে কলাম্বিয়া বিশ্ববিদ্যালয়ে আই. আই. রাবির নেতৃত্বাধীন একটি দল নিউক্লিয়াসের চৌম্বক মোমেন্ট নির্ণয়ের জন্য চৌম্বক অনুরণন কৌশল উদ্ভাবন করেছিল। এভাবে প্রাপ্ত পরিমাপ থেকে ১৯৩৯ সালে আবিষ্কৃত হয় যে ডিউটেরনে একটি তড়িৎ কোয়াড্রাপোল মোমেন্টও উপস্থিত রয়েছে।^[১৪]^[১৫] একটি প্রোটন এবং একটি নিউট্রন দ্বারা গঠিত ডিউটেরন হল সরলতম পারমাণবিক কাঠামোগুলোর একটি। এই আবিষ্কারের মাধ্যমে জানা যায় যে ডিউটেরনের কাঠামো সম্পূর্ণ প্রতিসম নয়, যা নিউক্লিয়নসমূহকে আবদ্ধকারী নিউক্লীয় বল সম্পর্কে মূল্যবান তথ্য প্রদান করেছিল। বিষেশত, ওই পরীক্ষার ফলাফল থেকে জানা গিয়েছিল যে নিউক্লীয় বলটি কোন কেন্দ্রীয় বল নয়, বরং একধরনের স্থিতিস্থাপক বৈশিষ্ট্যধারী।^[১] হানস বিথ এর মতে, ডিউটেরনের কোয়াড্রাপোল মোমেন্টের আবিষ্কার ছিল পারমাণবিক বিজ্ঞানের প্রথম দিকের একটি অন্যতম গুরুত্বপূর্ণ ধাপ।^[১৪]

ঐতিহাসিকভাবে, পারমাণবিক বলের প্রপঞ্চবৈজ্ঞানিক ব্যাখ্যা গঠন করা ছিল খুবই কঠিনসাধ্য। এই উদ্দেশ্যে প্রথম অর্ধ-পরীক্ষামূলক কাঠামোর উত্থাপিত ১৯৫০ এর দশকে, যেমন উড‌্স-স্যাক্সন বিভব প্রস্তাবনা (১৯৫৪)।^[১] ১৯৬০ এবং ৭০ এর দশকে নিউক্লীয় বল সম্পর্কিত তাত্ত্বিক এবং পরীক্ষমূলক উভয় ক্ষেত্রেই ব্যাপক প্রগতি ঘটে। এসময় অন্যতম প্রভাব বিস্তারকারী একটি তত্ত্ব ছিল রেইড বিভব (১৯৬৮)।^[১]

V_{\text{Reid}}(r)=-10.463{\frac {e^{-\mu r}}{\mu r}}-1650.6{\frac {e^{-4\mu r}}{\mu r}}+6484.2{\frac {e^{-7\mu r}}{\mu r}}

সাম্প্রতিক গবেষণাসমূহ নিউক্লীয় শক্তির সুক্ষ্মতর বিষয়ে মনোযোগ দিচ্ছে, যেমন, চার্জের সঙ্গে এর সম্পর্ক, πNN যুগল ধ্রুবকের নিখুঁত মান নির্ণয়, দশা পরিবর্তন ক্রিয়ার উন্নত বিশ্লেষণ, উচ্চতর সুক্ষ্মতার NN বিভব এবং NN উপাত্ত , মধ্য থেকে উচ্চ শক্তিতে NN বিক্ষেপণ,এবং QCD থেকে পারমাণবিক বলে উপনীত হবার প্রচেষ্টা।

সবল মিথষ্ক্রিয়ার অবশেষ হিসেবে ব্যাখ্যা[সম্পাদনা]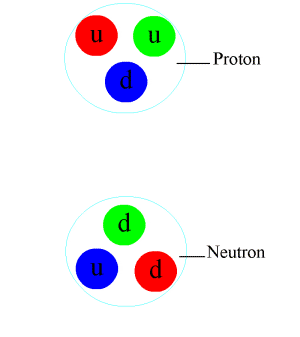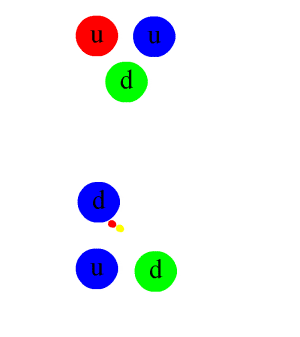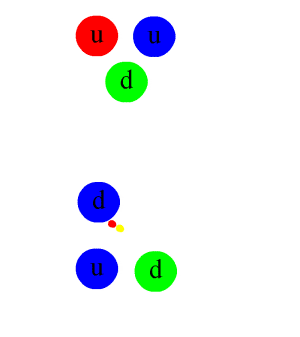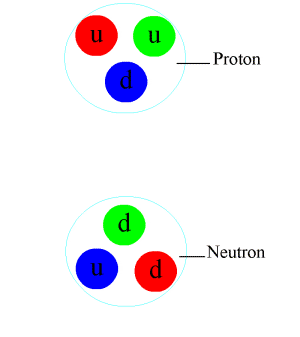

মিথষ্ক্রিয়ার অ্যানিমেশন। ক্ষুদ্র রঙিন বৃত্তযুগল হল গ্লুয়ন। রঙগুলো এই ডায়াগ্রাম ^{(বিবর্ধিত)} অনুসারে নির্ধারিত হয়েছে।

পারমাণবিক বলটি মৌলিক সবল মিথষ্ক্রিয়ার অবশিষ্টাংশ। সবল মিথষ্ক্রিয়া হল একটি আকর্ষক বল যা কোয়ার্কের মধ্যে ক্রিয়া করে নিউক্লিয়নসমূহ গঠন করে। এই বল গ্লুয়ন দ্বারা প্রবাহিত হয়। গ্লুয়ন কণা তড়িৎ চার্জের মত তবে তার চেয়ে শক্তিশালী রঙিন চার্জ দ্বারা কোয়ার্কগুলোকে আবদ্ধ রাখে। কোয়ার্ক, গ্লুয়ন প্রভৃতির ক্রিয়াকলাপ নিউক্লিয়নের মধ্যেই সীমিত থাকে, তবে তার প্রভাবক্ষেত্র নিউক্লিয়ন সীমানার কিছুটা বাইরে প্রসারিত হয়, এবং পারমাণবিক বলের জন্ম দেয়।

নিউক্লীয় বলগুলো নিউক্লিয়নসমূহের ভিতর কাজ করে, এবং রসায়নে বর্ণিত অণু-পরমাণুর অন্তস্থ লন্ডন শক্তির অনুরূপ। পরমাণুর গাঠনিক তড়িৎ-আকর্ষণ (যেমন নিউক্লিয়াস ও ইলেকট্রনের মধ্যস্থ বল) অপেক্ষা এধরনের বল অনেকটাই ক্ষীণ, এবং এদের প্রভাবক্ষেত্র খুবই সংকীর্ণ, কারণ এসব বল নিরপেক্ষ পরমাণুর অভ্যন্তরে খুবই ক্ষুদ্র চার্জ পার্থক্য থেকে উৎপন্ন। একইভাবে, নিউক্লিয়নসমূহ গ্লুয়নের শক্তি বাতিলকারী কোয়ার্ক দ্বারা গঠিত হলেও কোয়ার্ক-গ্লুয়নের কিছু সমন্বয় নিউক্লিয়ন থেকে ছাড়া পায়, এবং অল্প-পাল্লার নিউক্লীয় বলক্ষেত্র হিসেবে প্রতীয়মান হয়, যা অল্প দূরত্বে এক নিউক্লিয়ন থেক অন্য নিউক্লিয়নে কাজ করতে পারে। তবে এই নিউক্লীয় বল, নিউক্লিয়নের অন্তস্থ গ্লুয়ন বল অপেক্ষা খুবই দুর্বল, এবং খুবই অল্প পরিসরে কার্যকর থাকে। তথাপি, এই বল ক্ষুদ্র দূরত্বে নিউট্রন ও প্রোটনকে আবদ্ধ রাখার মত শক্তিশালী, এবং নিউক্লিয়াসে প্রোটনসমূহের তড়িৎ বিকর্ষণকে পরাস্ত করতে সক্ষম।

কখনও কখনও নিউক্লীয় বলকে অবশিষ্ট সবল বল (residual strong force) বলা হয়। এই নামটি ১৯৭০ সালে QCD তত্ত্ব গঠনকালে প্রচলিত হয়েছে। এর পূর্বে সবল নিউক্লীয় বল বলতে আন্ত-নিউক্লিয়ন বিভব বোঝানো হত, তবে কোয়ার্ক কাঠামো বিকশিত হবার পর QCD এর অর্থে ব্যবহৃত হচ্ছে।

নিউক্লিয়ন–নিউক্লিয়ন বিভব[সম্পাদনা]

দ্বি-নিউক্লিয়ন কাঠামোতে, যেমন ডিউটেরনে, পরমাণুর নিউক্লিয়াস এবং প্রোটন-প্রোটন ও নিউট্রন-প্রোটন জুটিগুলো NN বল পরীক্ষার জন্য উত্তম। নিউক্লিয়নগুলোতে ইউকাওয়া পটেনশিয়ালের মত একটি বিভব প্রয়োগ করে তা শ্রোডিঙার সমীকরণের সাহায্যে এ কাঠামোর ব্যাখ্যা করা সম্ভব। বিভবটির গঠন প্রপঞ্চবৈজ্ঞানিকভাবে পরিমাপ দ্বারা পাওয়া যায়, তবে দূরপাল্লার মিথষ্ক্রিয়ার ক্ষেত্রে মেসন-হস্তান্তর তত্ত্বও সহায়তা করে। বিভবের বৈশিষ্ট্য নির্ণয় করা হয় নিরীক্ষামূলক উপাত্ত থেকে, যেমন ডিউটেরনের যোজন শক্তি, NN দশান্তর, কিংবা NN স্থিতিস্থাপক বিক্ষেপণের প্রস্থচ্ছেদ।

সর্বাধিক প্রচলিত NN বিভবসমূহ হল প্যারিস, আর্গন এভি১৮,^[১৬] সিডি-বন, এবং নিমেজেন বিভব।

আধুনিকতর একটি পদ্ধতি হল নিউক্লিয়ন-নিউক্লিয়ন এবং ত্রি-নিউক্লিয়ন ব্যবস্থার ব্যাখ্যার জন্য প্রযোজ্য কার্যকর ক্ষেত্র তত্ত্ব গঠন করা। কোয়ান্টাম হ্যাড্রোডায়নামিক্স ক্ষেত্র তত্ত্বটি পারমাণবিক বলের জন্য উপযুক্ত; এটি রঞ্জন মিথষ্ক্রিয়ার জন্য QCD এবং তড়িৎচুম্বকীয় মিথষ্ক্রিয়ায় QED এর সাথে তুলনীয়। উপরন্তু, একটি কার্যকর ক্ষেত্র তত্ত্ব (কাইরাল বিচলন তত্ত্ব) ব্যবহার করে কাইরাল প্রতিসাম্য লঙ্ঘনের ঘটনাও নীরিক্ষা করা যায়, এবং পাইয়ন বিনিময় কণার মধ্যস্থতায় নিউক্লিয়নের মিথষ্ক্রিয়ায় বিচলন গণনায়ও সাহায্য করে।

নিউক্লিয়ন থেকে নিউক্লিয়াস[সম্পাদনা]

নিউক্লীয় পদার্থবিজ্ঞানের সামগ্রিক লক্ষ্য হল নিউক্লিয় মিথষ্ক্রিয়া দ্বারা সমস্ত পারমাণবিক ক্রিয়াকলাপের ব্যাখ্যা করা। একে মাইক্রোস্কোপিক বা ab initio পদ্ধতি বলা হয়। তবে এই লক্ষ্য অর্জনের পথে দুটি বড় বাধা উপস্থিত:

বহু-বস্তু কাঠামোতে গণনার জন্য খুব জটিল এবং উন্নত কৌশল প্রয়োজন।
প্রমাণ পাওয়া গেছে যে ত্রি-নিউক্লিয়ন বল (ও সম্ভাব্য উচ্চতর বহু-কণা মিথষ্ক্রিয়া) এক্ষেত্রে গুরুত্বপূর্ণ ভূমিকা পালন করে। অতএব এবিষয়ক কাঠামোতে তিন-নিউক্লিয়ন বিভব অন্তর্ভুক্ত করা আবশ্যক।

এটি একটি সক্রিয় গবেষণাক্ষেত্র। সর্বোচ্চ A = ১২ ভর সংখ্যার জন্য দুই- এবং তিন-নিউক্লিয়ন বিভব গণনার কৌশল আবিষ্কৃত হয়েছে। কম্পিউটেশন কৌশলে প্রতিনিয়ত উৎকর্ষ সাধনের মাধ্যমে নিউক্লীয় শেলের সুক্ষ্মতর গঠনবর্ণনা অর্জিত হচ্ছে।

পারমাণবিক বিভব[সম্পাদনা]

নিউক্লিয় মিথষ্ক্রিয়া বর্ণনার একটি উপায় হল স্বতন্ত্র নিউক্লিয়নসমূহের পরিবর্তে সম্পূর্ণ নিউক্লিয়াসের জন্য বিভব গণনা করা। একে ম্যাক্রোস্কোপিক পদ্ধতি বলা হয়। যেমন, নিউক্লিয়াসের বিভবে বাস্তব ও অবাস্তব অংশের সমন্বয়ে গঠিত একটি সমতলীয় তরঙ্গের সাহায্যে নিউক্লিয়াস থেকে নিউট্রনের বিক্ষেপণ ব্যাখ্যা করা যায়। এই কাঠামোটিকে অনেক সময় দৃশ্যমান বা অপটিকাল কাঠামো বলা হয় কারণ এটি অস্বচ্ছ কাঁচ গোলকে আলোক বিক্ষেপণের অনুরূপ।

নিউক্লিয় বিভব স্থানীয় অথবা সার্বজনীন হতে পারে। স্থানীয় বিভব সংকীর্ণ শক্তিসীমা বা সংকীর্ণ নিউক্লিয় ভরসীমার মধ্যে কার্যকর। অন্যদিকে সার্বজনীন বিভব শক্তি ও ভরের ফাংশন বলে যেকোন মানের শক্তি ও ভরের সাপেক্ষে কার্যকর। সার্বজনীন বিভব অপেক্ষাকৃত জটিল এবং গণনায় নির্ভুলতা কম, তবে এর বাস্তবিক প্রয়োগক্ষেত্র ব্যাপক।

আরও দেখুন[সম্পাদনা]

তথ্যসূত্র[সম্পাদনা]

↑ ^ক ^খ ^গ ^ঘ Reid, R.V. (১৯৬৮)। "Local phenomenological nucleon–nucleon potentials"। Annals of Physics। 50: 411–448। ডিওআই:10.1016/0003-4916(68)90126-7। বিবকোড:1968AnPhy..50..411R।
↑ Kenneth S. Krane (১৯৮৮)। Introductory Nuclear Physics। Wiley & Sons। আইএসবিএন 0-471-80553-X।
↑ Binding Energy, Mass Defect ওয়েব্যাক মেশিনে আর্কাইভকৃত ১৮ জুন ২০১৭ তারিখে, Furry Elephant physics educational site, retr 2012 7 1
↑ Chapter 4 NUCLEAR PROCESSES, THE STRONG FORCE, M. Ragheb 1/30/2013, University of Illinois
↑ Povh, B.; Rith, K.; Scholz, C.; Zetsche, F. (২০০২)। Particles and Nuclei: An Introduction to the Physical Concepts। Berlin: Springer-Verlag। পৃষ্ঠা 73। আইএসবিএন 978-3-540-43823-6।
↑ Stern, Dr. Swapnil Nikam (ফেব্রুয়ারি ১১, ২০০৯)। "Nuclear Binding Energy"। "From Stargazers to Starships"। NASA website। সংগ্রহের তারিখ ২০১০-১২-৩০।
↑ Griffiths, David, Introduction to Elementary Particles
↑ Heisenberg, W. (১৯৩২)। "Über den Bau der Atomkerne. I"। Z. Phys.। 77: 1–11। ডিওআই:10.1007/BF01342433। বিবকোড:1932ZPhy...77....1H।
↑ Heisenberg, W. (১৯৩২)। "Über den Bau der Atomkerne. II"। Z. Phys.। 78 (3–4): 156–164। ডিওআই:10.1007/BF01337585। বিবকোড:1932ZPhy...78..156H।
↑ Heisenberg, W. (১৯৩৩)। "Über den Bau der Atomkerne. III"। Z. Phys.। 80 (9–10): 587–596। ডিওআই:10.1007/BF01335696। বিবকোড:1933ZPhy...80..587H।
↑ Iwanenko, D.D., The neutron hypothesis, Nature 129 (1932) 798.
↑ Miller A. I. Early Quantum Electrodynamics: A Sourcebook, Cambridge University Press, Cambridge, 1995, আইএসবিএন ০৫২১৫৬৮৯১৯, pp. 84–88.
↑ Brown, L.M.; Rechenberg, H. (১৯৯৬)। The Origin of the Concept of Nuclear Forces। Bristol and Philadelphia: Institute of Physics Publishing। আইএসবিএন 0750303735।
↑ ^ক ^খ John S. Rigden (১৯৮৭)। Rabi, Scientist and Citizen। New York: Basic Books, Inc.। পৃষ্ঠা 99–114। আইএসবিএন 9780674004351। সংগ্রহের তারিখ মে ৯, ২০১৫।
↑ Kellogg, J.M.; Rabi, I.I.; Ramsey, N.F.; Zacharias, J.R. (১৯৩৯)। "An electrical quadrupole moment of the deuteron"। Physical Review। 55: 318–319। ডিওআই:10.1103/physrev.55.318। বিবকোড:1939PhRv...55..318K। সংগ্রহের তারিখ মে ৯, ২০১৫।
↑ Wiringa, R. B.; Stoks, V. G. J.; Schiavilla, R. (১৯৯৫)। "Accurate nucleon–nucleon potential with charge-independence breaking"। Physical Review C। 51: 38। arXiv:nucl-th/9408016 । ডিওআই:10.1103/PhysRevC.51.38। বিবকোড:1995PhRvC..51...38W।

গ্রন্থপঞ্জি[সম্পাদনা]

Gerald Edward Brown and A. D. Jackson, The Nucleon–Nucleon Interaction, (1976) North-Holland Publishing, Amsterdam আইএসবিএন ০-৭২০৪-০৩৩৫-৯
R. Machleidt and I. Slaus, "The nucleon–nucleon interaction", J. Phys. G 27 (2001) R69 (topical review).
E.A. Nersesov, Fundamentals of atomic and nuclear physics, (1990), Mir Publishers, Moscow, আইএসবিএন ৫-০৬-০০১২৪৯-২
P. Navrátil and W.E. Ormand, "Ab initio shell model with a genuine three-nucleon force for the p-shell nuclei", Phys. Rev. C 68, 034305 (2003).