পয়সোঁ বিন্যাস
সম্ভাবনা ভর ফাংশন 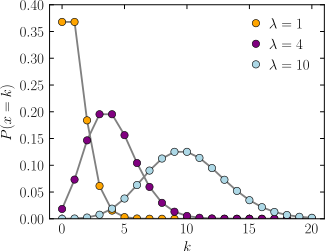 The horizontal axis is the index k, the number of occurrences. λ is the expected number of occurrences, which need not be an integer. The vertical axis is the probability of k occurrences given λ. The function is defined only at integer values of k. The connecting lines are only guides for the eye. | |
ক্রমযোজিত বিন্যাস ফাংশন 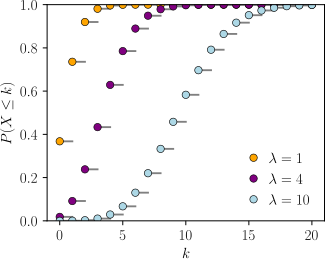 The horizontal axis is the index k, the number of occurrences. The CDF is discontinuous at the integers of k and flat everywhere else because a variable that is Poisson distributed takes on only integer values. | |
| সূচক | |
|---|---|
| পরামিতি | (real) — rate |
| ব্যবধি | |
| পিএমএফ | |
| সিডিএফ | , or , or (for , where is the upper incomplete gamma function, is the floor function, and Q is the regularized gamma function) |
| গড় | |
| মধ্যমা | |
| প্রচুরক | |
| ভেদাঙ্ক | |
| বঙ্কিমতা | |
| বর্ধিত সূচালতা | |
| এনট্রপি |
(for large ) |
| এমজিএফ | |
| পিজিএফ | |
| বৈশিষ্ট্য ফাংশন | |
| ফিশার তথ্য | |
পরিসংখ্যান ও সম্ভাবনা তত্ত্বে পয়সোঁ বিন্যাস একটি বিচ্ছিন্ন সম্ভাবনা বিন্যাস। ফরাসি গণিতবিদ সিমেওঁ দ্যনি পোয়াসোঁ এর নাম থেকে বিন্যাসটির নাম নেওয়া হয়েছে। বিন্যাসটি নির্দিষ্ট পরিমাণ সময় বা স্থানের ব্যাপ্তিতে ঘটা ঘটনার সংখ্যার সম্ভাবনা প্রকাশ করে, যেখানে ঘটনাগুলো একটি জানা নির্দিষ্ট হারে ঘটে এবং সর্বশেষ ঘটনার পরের সময়ের ওপর অনির্ভরশীল হয়[১] দূরত্ব, ক্ষেত্রফল বা আয়তন বা এ ধরনের অন্য নির্দিষ্ট ব্যাপ্তির ক্ষেত্রেও পয়সোঁ বিন্যাস ব্যবহার করা যেতে পারে।
উদাহরণস্বরূপ, কেউ যদি প্রতিদিন পাওয়া চিঠির পরিমাণের হিসাব রাখেন, তাহলে হয়ত দেখা যাবে প্রতি দিন গড়ে ৪টি চিঠি আসছে। যদি নির্দিষ্ট কোনো চিঠি ভবিষ্যতের কোনো চিঠি আসার সময়কে প্রভাবিত না করে, অর্থাৎ যদি চিঠিগুলো অনেকগুলো আলাদা আলাদা উৎস থেকে স্বাধীনভাবে আসে, তাহলে প্রতি দিন পাওয়া চিঠির সংখ্যা পয়সোঁ বিন্যাস মেনে চলবে ধরে নেওয়া একটি যুক্তিসঙ্গত অনুমান হবে।[২] পয়সোঁ বিন্যাসের অন্যান্য উদাহরণের মধ্যে রয়েছে কোনো কল সেন্টারে প্রতি ঘণ্টায় আসা ফোন কলের সংখ্যা ও কোনো তেজস্ক্রিয় উৎস থেকে প্রতি সেকেন্ডে ক্ষয়কৃত কণার সংখ্যা।
মৌলিক ধারণা[সম্পাদনা]
নির্দিষ্ট পরিমাণ সময় বা স্থানের ব্যাপ্তিতে ঘটা ঘটনার সংখ্যার মডেল তৈরিতে পয়সোঁ বিন্যাস খুব জনপ্রিয়।
উদাহরণ[সম্পাদনা]
নিচের ঘটনার ক্ষেত্রে পয়সোঁ বিন্যাসের সাহায্যে মডেল তৈরি করা যেতে পারে-
- প্রতি বছর এক মিটারের বেশি ব্যাসের যে পরিমাণ উল্কাপিণ্ড পৃথিবীর বুকে আঘাত হানে
- সকাল ১০টা থেকে রাত ১১টার মধ্যে যে পরিমাণ রোগী ইমারজেন্সি কক্ষে আসেন
- নির্দিষ্ট পরিমাণ সময়ের মধ্যে যে পরিমাণ ফোটন একটি ডিটেক্টরে ধরা পড়ে
অনুমান ও বৈধতা[সম্পাদনা]
নিচের অনুমানগুলো সত্য হলে পয়সোঁ বিন্যাসকে উপযুক্ত মডেল হিসেবে বিবেচনা করা যাবে।
- কোনো একটি নির্দিষ্ট ব্যাপ্তিতে ঘটনার সংখ্যাকে k দিয়ে প্রকাশ করলে যদি k এর মান হতে পারে ০, ১, ২, ...।
- কোনো ঘটনা পরবর্তী ঘটনা ঘটার সম্ভাবনাকে প্রভাবিত করবে না। অর্থাৎ, ঘটনাগুলো হবে স্বাধীন।
- ঘটনা ঘটার গড় হার হবে ধ্রুব।
- দুটি ঘটনা ঠিক একই সময়ে ঘটবে না। বরং, অতি ক্ষুদ্র ব্যাপ্তিতে কোনো ঘটনা হয় ঘটবে নয়ত ঘটবে না।
অথবা
- প্রকৃত সম্ভাবনা বিন্যাস হবে দ্বিপদী বিন্যাস এবং চেষ্টার (trial) সংখ্যা সংশ্লিষ্ট সফলতার সংখ্যার চেয়ে যথেষ্ট বড় হবে।
এই শর্তগুলো সত্য হলে k হবে একটি পয়সোঁ দৈব চলক আর k এর বিন্যাস হবে একটি পয়সোঁ বিন্যাস।
পয়সোঁ বিন্যাসে ঘটনার সম্ভাবনা[সম্পাদনা]
কোনো ব্যাপ্তিতে একটি ঘটনা ০, ১, ২, ... বার ঘটতে পারে। ব্যাপ্তির ঘটনার গড় সংখ্যাকে (ল্যামডা) দ্বারা প্রকাশ করা হয়। হলো ঘটনার হার, যাকে হার পরামিতিও বলা হয়। কোনো ব্যাপ্তিতে k সংখ্যক ঘটনা পর্যবেক্ষণ করার সম্ভাবনা
সমীকরণটি দিয়ে প্রকাশ করা যাবে, যেখানে
- হলো প্রতি ব্যাপ্তিতে ঘটনার গড় সংখ্যা
- e হলো একটি সংখ্যা, যার মান 2.71828... (অয়লার সংখ্যা ও প্রাকৃতিক লগারিদমের ভিত্তি)
- k এর মান হতে পারে ০, ১, ২, ...
- k! = k × (k − 1) × (k − 2) × … × 2 × 1 হলো k এর ফ্যাক্টরিয়াল।
এই সমীকরণটি হলো পয়সোঁ বিন্যাসের সম্ভাবনা ভর ফাংশন। লক্ষ্যনীয় যে, গড় ঘটনা এর বদলে ঘটনা ঘটার সময়ের হার দেওয়া থাকলেও সমীকরণটির পরিবর্তিত রূপ ব্যবহার করা যাবে। সেক্ষেত্রে হবে (যেখানে এর একক হলো ১/সময়) এবং
পয়সোঁ বিন্যাসে সম্ভাবনার উদাহরণ[সম্পাদনা]
কোনো একটি নির্দিষ্ট নদীতে গড়ে প্রতি একশত বছরে একবার অতিপ্রবাহের কারণে বন্যা হয়। পয়সোঁ মডেলকে উপযুক্ত ধরে নিয়ে ১০০ বছরের ব্যাপ্তিতে এমন k = ০, ১, ২, ৩, ৪, ৫ বা ৬টি বন্যা হবে তার সম্ভাবনা বের করা সম্ভব। এখানে গড় ঘটনার হার হলো প্রতি ১০০ বছরে একটি অতিপ্রবাহ। অর্থাৎ, λ = 1
১০০ বছর সময়কালের মধ্যে ০ থেকে ৬টি অতিপ্রবাহের সম্ভাবনা নিচের সারণিতে দেওয়া আছে।
| k | P(k overflow floods in 100 years) |
|---|---|
| 0 | 0.368 |
| 1 | 0.368 |
| 2 | 0.184 |
| 3 | 0.061 |
| 4 | 0.015 |
| 5 | 0.003 |
| 6 | 0.0005 |
উগারতে ও তার সহকর্মীরা জানিয়েছেন, ফুটবল বিশ্বকাপের একটি ম্যাচে গড় গোলের সংখ্যা প্রায় ২.৫ এবং পয়সোঁ মডেলের ব্যবহার যথাযথ।[৩] যেহেতু প্রতি ম্যাচে গোলের গড় সংখ্যা ২.৫, অতএব λ = 2.5।
নিচের সারণিতে কোনো ম্যাচে ০ থেকে ৭টি গোল হবার সম্ভাবনা দেওয়া আছে।
| k | P(k goals in a World Cup soccer match) |
|---|---|
| 0 | 0.082 |
| 1 | 0.205 |
| 2 | 0.257 |
| 3 | 0.213 |
| 4 | 0.133 |
| 5 | 0.067 |
| 6 | 0.028 |
| 7 | 0.010 |
প্রতি ব্যাপ্তিতে একবার ঘটা ঘটনা: λ = 1 ও k = 0 এর বিশেষ অবস্থা[সম্পাদনা]
ধরা যাক, জ্যোতির্বিদগণ হিসেব করে পেলেন যে বড় বড় উল্কাপিণ্ড (নির্দিষ্ট আকারের চেয়ে বড়) প্রতি ১০০ বছরে একবার পৃথিবীতে আঘাত হানে (প্রতি ১০০ বছরে λ = 1টি ঘটনা)। আরও দেখলেন যে পৃথিবীকে আঘাত করা এই আকারে উল্কাপিণ্ডের সংখ্যা পয়সোঁ বিন্যাস মেনে চলে। তাহলে পরবর্তী ১০০ বছরে k = 0টি উল্কাপিন্ড আঘাত হানবে তার সম্ভবনা কত?
এ অনুমানগুলো মেনে নিলে দেখা যায়, পরবর্তী ১০০ বছরে বড় কোনো উল্কাপিণ্ড পৃথিবীতে আঘাত হানবে না এমন সম্ভাবনা প্রায় ০.৩৭। বাকি ১ − ০.৩৭ = ০.৬৩ হলো পরবর্তী ১০০ বছরে ১, ২, ৩ বা আরও বেশি সংখ্যক বড় উল্কাপিণ্ড আঘাত হানার সম্ভাবনা। ওপরের একটি উদাহরণে অতিপ্রবাহজনিত বন্যা প্রতি ১০০ বছরে ১ বার ঘটেছিল (λ = 1)। একই হিসাব অনুসারেই ১০০ বছরে অতিপ্রবাহজনিত কোনো বন্যা না হবার সম্ভাবনা ছিল ০.৩৭। সাধারণভাবে প্রতি ব্যাপ্তিতে কোনো ঘটনা গড়ে একবার ঘটলে (λ = 1) এবং ঘটনাগুলো পয়সোঁ বিন্যাস মেনে চললে P(পরবর্তী ব্যাপ্তিতে ০টি ঘটনা) = ০.৩৭। এছাড়া, P(পরবর্তী ব্যাপ্তিতে শুধু একটি ঘটনা) = ০.৩৭, যেটা অতিপ্রবাহজনিত বন্যার সারণিতে দেখানো হয়েছে।
পয়সোঁ অনুমান মেনে চলে না এমন উদাহরণ[সম্পাদনা]
কোনো ছাত্র পরিষদে প্রতি মিনিটে উপস্থিত হওয়া ছাত্রদের সংখ্যা পয়সোঁ বিন্যাস নাও মেনে চলতে পারে, কারণ এখানে হার ধ্রুবক নয় (ক্লাস চলাকালে হার কম এবং ক্লাসের ফাঁকে হার বেশি)। আবার ছাত্রদের আসার ঘটনা স্বাধীনও নয় (ছাত্ররা সাধারণত দল বেঁধে আসে)। একটি বড় ভূমিকম্পের কারণে সমমাত্রার আফটারশকের সম্ভাবনা বেড়ে গেলে কোনো দেশে প্রতি বছর সংঘটিত ৫ মাত্রার ভূমিকম্পের সংখ্যা পয়সোঁ বিন্যাস নাও মেনে চলতে পারে। কোনো হাসপাতালের নিবিড় পরিচর্যা কেন্দ্রে ভর্তি রোগীদের ক্ষেত্রে অবস্থানের দিনের সংখ্যা পয়সোঁ বিন্যাস মেনে চলবে না, কারণ দিনের সংখ্যা শূন্য হওয়া সম্ভব নয়। এই বিন্যাসকে শূন্য-বিহীন পয়সোঁ বিন্যাসের সাহায্যে মডেল করা যেতে পারে। যে সকল গণনা বিন্যাসে শূন্যটি ঘটনার ব্যাপ্তির সংখ্যা পয়সোঁ মডেলের অনুমানের চেয়ে বেশি সেক্ষেত্রে শূন্য-স্ফীত মডেল ব্যবহার করা যেতে পারে।
পয়সোঁ নির্ভরণ ও ঋণাত্মক দ্বিপদী নির্ভরণ[সম্পাদনা]
অধীন চলক গণনাবাচক হলে অর্থাৎ কোনো ব্যাপ্তিতে ঘটনার সংখ্যা (০, ১, ২, ...) হলে পয়সোঁ নির্ভরণ ও ঋণাত্মক দ্বিপদী নির্ভরণ খুব ভালোভাবে কাজে লাগানো যায়।
ইতিহাস[সম্পাদনা]
সিমেওঁ দ্যনি পোয়াসোঁ (১৭৮১-১৮৪০) তাঁর ১৮৩১ সালের Recherches sur la probabilité des jugements en matière criminelle et en matière civile (ফৌজদারী ও বেসামরিক বিষয়াদি সম্পর্কিত রায়ের সম্ভাবনা বিষয়ক গবেষণা) কাজে সম্ভাবনা তত্ত্বের সাথে বিন্যাসটি সর্বপ্রথম প্রবর্তন ও প্রকাশ করেন।[৪] কাজটিতে একটি দৈব চলক N ব্যবহারের মাধ্যমে কোনো নির্দিষ্ট দেশের অন্যায় রায়ের সংখ্যা সম্পর্কে তত্ত্ব দেওয়া হয়। এই N অন্যান্য জিনিসের মধ্যে গণনা করে যে একটি নির্দিষ্ট সময় ব্যাপ্তিতে কতটি বিচ্ছিন্ন ঘটনা ঘটেছে। এই ফলাফল এর আগে আব্রাআম দ্য মোয়াভ্র্ও (১৭১১) ফিলোসোফিকেল ট্রাঞ্জেকশন অব রয়েল সোসাইটি জার্নালে De Mensura Sortis seu; de Probabilitate Eventuum in Ludis a Casu Fortuito Pendentibus নামে প্রকাশিত নিবন্ধে দেখিয়েছিলেন। এ কারণে এটি স্টিগলারের নিয়মেরও একটি উদাহরণ। আর এ কারণে অনেকে বলেছেন পয়সোঁ বিন্যাসে দ্য মোয়াভ্ররের নাম থাকা উচিত।[৫][৬] ১৮৯৮ সালে বিন্যাসটির একটি বাস্তব প্রয়োগ দেখিয়েছেন লাদিসলাউস বরতিকিউইসজ। তাঁকে প্রুশিয়ান সেনাবাহিনীতে ঘোড়ার পদাঘাতে দূর্ঘটনাক্রমে মারা যাওয়া সৈন্যের সংখ্যা নিয়ে তদন্ত করতে বলা হলে সে কাজের অংশ হিসেবে তিনি পয়সোঁ বিন্যাসের প্রয়োগ ঘটনা। এই পরীক্ষণের মাধ্যমে পয়সোঁ বিন্যাস নির্ভরযোগ্যতা প্রকৌশল শাস্ত্রে অন্তর্ভূক্ত হয়।[৭]
সংজ্ঞা[সম্পাদনা]
একটি বিচ্ছিন্ন দৈব চলক X , λ > 0 পরামিতির একটি পয়সোঁ বিন্যাস মেনে চলবে যদি k = 0, 1, 2, ..., এর জন্য X এর সম্ভাবনা ভর ফাংশন এ রকম হয়:[৮]
যেখানে
- e হলো অয়লার সংখ্যা (e = 2.71828...)।
- k! হলো k এর ফ্যাক্টোরিয়াল।
ধনাত্মক বাস্তব সংখ্যা λ হবে X এর প্রত্যাশিত মান ও ভেদাঙ্কের সমান।[৯]
অনেক বেশি সংখ্যক সম্ভাব্য ঘটনার প্রতিটি দুর্লভ ঘটনা হলে পয়সোঁ বিন্যাস ব্যবহার করা যেতে পারে। একটি নির্দিষ্ট সময় ব্যাপ্তিতে ঐ রকম কতগুলো ঘটনা ঘটবে সেটা উপযুক্ত পরিস্থিতিতে পয়সোঁ বিন্যাসের একটি দৈব সংখ্যা হবে। পয়সোঁ বিন্যাসের প্রচলিত সংজ্ঞায় এমন দুটি এমন দুটি পদ আছে যেগুলোর কারণে কম্পিউটার দিয়ে বিন্যাসটির কাজ করা সহজেই অসম্ভব হয়ে পড়ে। এগুলো হলো λk ও k!। এছাড়াও λk কে k! দ্বারা ভাগ দিলে যে আসন্নীকরণ ত্রুটি ঘটে তাও e−λ এর তুলনায় অনেক বড়। এ কারণে ভুল ফলাফল পাওয়া যায়। সংখ্যাভিত্তিক স্থিতিশীলতার জন্য পয়সোঁ সম্ভাবনা ভর ফাংশন এভাবে বের করা উচিত:
যা গাণিতিকভাবে সমতুল্য কিন্তু সংখ্যাভিত্তিকভাবে স্থিতিশীল। C প্রোগ্রামিং ল্যাংগুয়েজের আদর্শ লাইব্রেরি (C99) থেকে lgamma ফাংশন, R প্রোগ্রামিং ল্যাংগুয়েজ, ম্যাটল্যাবের gammaln ফাংশন, SciPy বা ফোরট্রানের ২০০৮ বা তার পরবর্তী সংস্করণের log_gamma ফাংশন ব্যবহার করে গামা ফাংশনের স্বাভাবিক লগারিদম বের করা যায়।
বৈশিষ্ট্য[সম্পাদনা]
বর্ণনামূলক পরিসংখ্যান[সম্পাদনা]
- পয়সোঁ বিন্যাস মেনে চলা দৈব চলকের প্রত্যাশিত মান ও ভেদাঙ্ক দুটিই λ।
- বিভেদাঙ্ক হলো এবং বিস্তার সূচকের মান ১।
- গড় পরম ব্যবধান হলো:
- λ অপূর্ণ সংখ্যা হলে পয়সোঁ বিন্যাসের দৈব চলকের প্রচুরক হবে , যার অর্থ হলো λ এর সমান বা ছোট পূর্ণ সংখ্যা। একে floor(λ) আকারেও লেখা হয়। λ ধনাত্মক পূর্ণসংখ্যা হলে প্রচুরক হবে λ ও λ-1।
- পয়সোঁ বিন্যাসের সবগুলো ক্রমযোজিত মান প্রত্যাশিত মান λ এর সমান হবে। পয়সোঁ বিন্যাসের nতম ফ্যাক্টোরিয়াল পরিঘাত হলো λn।
- পয়সোঁ প্রক্রিয়ার প্রত্যাশিত মানকে অনেক সময় তীব্রতা ও এক্সপোজারের (যাকে আরও সাধারণভাবে বলা যায় সময় বা স্থানের সাপেক্ষে তীব্রতা ফাংশনের ইন্টিগ্রাল) গুণফল আকারে লেখা হয়।[১০][১১]
মধ্যমা[সম্পাদনা]
বিন্যাসটির মধ্যমা (ν) জানা আছে এবং এটি খুব তীক্ষ্ণ:[১২]
উচ্চতর পরিঘাত[সম্পাদনা]
- মূলের সাপেক্ষে পয়সোঁ বিন্যাসের উচ্চতর পরিঘাত mkগুলো হলো λ এর তাচার্দ বহুপদী:
- যেখানে দ্বিতীয় বন্ধনীর ভেতরের পদটি হলো দ্বিতীয় প্রকারের স্টারলিং সংখ্যা।[১৩] বহুপদীর সহগগুলো আসে সমাবেশের সূত্র থেকে। বস্তুত, পয়সোঁ বিন্যাসের প্রত্যাশিত মান 1 হলে দোবিন্সকির সূত্র অনুসারে nতম পরিঘাত হবে n আকারের একটি সেটের বিভাজনসংখ্যার সমান।
পয়সোঁ দৈব চলকের সমষ্টি[সম্পাদনা]
যদি এর জন্য স্বাধীন হয় এবং হয়, তাহলে ।[১৪] বিপরীতভাবে বিবেচনা করলে পাওয়া যাবে রাইকভের উপপাদ্য, যেটি অনুসারে দুটি স্বাধীন দৈব চলকের সমষ্টি পয়সোঁ বিন্যাস মেনে চললে স্বাধীন দৈব চলকদুটিও পয়সোঁ বিন্যাস মেনে চলবে।[১৫]
অন্যান্য বৈশিষ্ট্য[সম্পাদনা]
- পয়সোঁ বিন্যাসগুলো হলো অসীমতক বিভাজ্য সম্ভাবনা বিন্যাস।[১৬][১৭]:159
- Pois(λ) থেকে Pois(λ0) এর নির্দেশিত কুলব্যাক-লেইবলার অপসরণ হলো
- ।
- পয়সোঁ দৈব চলক এর প্রান্তীয় সম্ভাবনার সীমা চেরনোফ সীমা থেকে নির্ণয় করা যায়।[১৮]
- ,
- যে অসমতাগুলো পয়সোঁ বিন্যাসের দৈব চলক এর সম্ভাবনা ফাংশনকে আদর্শ পরিমিত বিন্যাস ফাংশনের সাথে সম্পর্কিত করে সেগুলো হলো:[১৯]
- যেখানে হলো ওপরে উল্লিখিত নির্দেশিত কুলব্যাক-লেইবলার।
পয়সোঁ রেস[সম্পাদনা]
ধরা যাক, ও স্বাধীন দৈব চলক, যেখানে , তাহলে
এখানে ঊর্ধ্ব-সীমা প্রমাণ করা হয় আদর্শ চেরনোফ সীমা দিয়ে।
আবার হলো এর সম্ভাবনা, যেখানে , যার নিম্ন-সীমা হলো , যেখানে হলো আপেক্ষিক এনট্রপি। এভাবে নিম্ন-সীমাও প্রমাণ করা যায়। এছাড়াও সম্পর্ক দিয়ে শর্তহীন সম্ভাবনার নিম্ন-সীমা বের করলে ফলাফলটি পাওয়া যায়।[২০]
সম্পর্কিত বিন্যাস[সম্পাদনা]
- ও স্বাধীন হলে পার্থক্যটি স্কেলাম বিন্যাস মেনে চলবে।
- ও স্বাধীন হলে শর্তে একটি দ্বিপদী বিন্যাস মেনে চলবে।
- নির্দিষ্ট করে উল্লেখ করলে, হলে
- আরও সাধারণভাবে, X1, X2,..., Xn λ1, λ2,..., λn এর স্বাধীন পয়সোঁ দৈব চলক হলে এবং
- হলে । বস্তুত, ।
- যদি এবং X = k শর্তে একটি দ্বিপদী বিন্যাস মেনে চলে তাহলে Y একটি পয়সোঁ বিন্যাস মেনে চলবে। বস্তুত, X = k শর্তে একটি বহুপদী বিন্যাস মেনে চলবে। অর্থাৎ, হলে প্রতিটি একটি স্বাধীন পয়সোঁ বিন্যাস মেনে চলবে।
- দ্বিপদী বিন্যাসের চেষ্টাসংখ্যা অসীম হলে এবং সফলতার সংখ্যার প্রত্যাশিত মান ধ্রুব থাকলে বিন্যাসটির একটি সীমাস্থ অবস্থা হিসেবে পয়সোঁ বিন্যাস নির্ণয় করা যায়। অতএব, দ্বিপদী বিন্যাসের
n যথেষ্ট বড় হলে এবং pp যথেষ্ট ছোট হলে পয়সোঁ বিন্যাস দিয়ে দ্বিপদী বিন্যাসের খুব কাছাকাছি মান বের করা সম্ভব। একটি সাধারণ নীতি হলো, পয়সোঁ বিন্যাস দিয়ে দ্বিপদী বিন্যাসের মান ভালোভাবে বের করা যাবে যদি n অন্তত ২০ এবং pp ০.০৫ এর সমান বা ছোট হয়। আর n ≥ 100 ও np ≤ 10 হলে আসন্ন মান হবে খুবই নিখুঁত।[২১]
- পয়সোঁ বিন্যাস বিচ্ছিন্ন যৌগিক পয়সোঁ বিন্যাসের একটিমাত্র পরমাতিযুক্ত একটি বিশেষ অবস্থা।[২২][২৩] একচলকযুক্ত বহুপদী বিন্যাসের সীমাস্থ বিন্যাস থেকে বিচ্ছিন্ন যৌগিক পয়সোঁ বিন্যাসে পৌঁছা যায়। এটি আবার যৌগিক পয়সোঁ বিন্যাসের একটি বিশেষ অবস্থা।
- λ এর বড় মানের জন্য (ধরা যাক λ>1000) λ গড় ও λ ভেদাঙ্কের (অর্থাৎ, পরিমিতি ব্যবধান ) পরিমিত বিন্যাস দিয়ে পয়সোঁ বিন্যাসের আসন্ন মান খুব ভালোভাবে বের করা যাবে। λ ১০ এর বড় হলে পরিমিত বিন্যাস দিয়ে ভালো আসন্ন মান পাওয়া যাবে যদি অবিচ্ছিন্নতা সংশোধন সঠিকভাবে করা হয়। অর্থাৎ, P(X ≤ x)কে P(X ≤ x + 0.5) দ্বারা প্রতিস্থাপিত করলে, যেখানে X একটি অঋণাত্মক পূর্ণসংখ্যা
- ভেদাঙ্ক স্থিতিশীলকরণ রুপান্তর: কোনো চলক পয়সোঁ বিন্যাস মেনে চললে এর বর্গমূলের বিন্যাস পরিমিত বিন্যাসের কাছাকাছি হবে, যেখানে প্রত্যাশিত মান হবে এবং ভেদাঙ্ক হবে ১/৪।[২৪][১৭]:163 এই রূপান্তরের ফলে অরূপান্তরিত চলকের চেয়ে দ্রুত হারে পরিমিত বিন্যাসের বৈশিষ্ট্য (λ বাড়ার সাথে সাথে) অর্জন করা যায়। ভেদাঙ্ক স্থিতিশীলকরণ রুপান্তরের আরও কিছু ও কিছুটা জটিল পদ্ধতিও আছে। এর মধ্যে অন্যতম হলো অ্যান্সকম্ব রূপান্তর।
- যদি প্রতিটি t > 0 এর জন্য সময় ব্যাপ্তি [0, t]তে ঘটনার সংখ্যা λt গড়ের পয়সোঁ বিন্যাস মেনে চলে তাহলে ঘটনা ঘটনার মধ্যবর্তী সময়ের অনুক্রম স্বাধীন হবে এবং সবাই 1/λ গড়ের সূচকীয় বিন্যাস মেনে চলবে।[২৫]
- পয়সোঁ ও কাই-বর্গ বিন্যাসের ক্রমযোজিত বিন্যাস ফাংশনের সম্পর্ক এমন:
- ও
সংঘটন[সম্পাদনা]
গণনা বিষয়ক অসংখ্য শাখায় পয়সোঁ বিন্যাসের প্রয়োগ দেখা যায়:[২৬]
- টেলিযোগাযোগে উদাহরণ: কোনো সিস্টেমে আসা কলের সংখ্যা
- জ্যোতির্বিদ্যায় উদাহরণ: টেলিস্কোপে আসা ফোটন কণার সংখ্যা
- রসায়নে উদাহরণ: জীবন্ত পলিমারকরণের মোলার ভর বিন্যাস[২৭]
- জীববিদ্যায় উদাহরণ: ডিএনএ-এর প্রতি একক দৈর্ঘ্যের সুতায় পরিব্যক্তির সংখ্যা।
- ব্যবস্থাপনায় উদাহরণ: কোনো কাউন্টার বা কল সেন্টারে আসা গ্রাহকের সংখ্যা।
- অর্থসংস্থান ও বিমা উদাহরণ: একটি নির্দিষ্ট সময়ে ক্ষতি বা ক্ষতিপূরণের সংখ্যা।
- ভূমিকম্পবিদ্যায় উদাহরণ: বড় ভূমিকম্পের ক্ষেত্রে ঝুঁকি বিষয়ক অসীমতক পয়সোঁ মডেল।[২৮]
- তেজস্ক্রিয়তায় উদাহরণ: নির্দিষ্ট সময়ে একটি তেজস্ক্রিয় নমুনার ক্ষয়ের সংখ্যা।
পয়সোঁ বিন্যাস মূলত পয়সোঁ প্রক্রিয়া থেকে আসে। বিচ্ছিন্ন বৈশিষ্ট্যযুক্ত (অর্থাৎ, যে ঘটনাগুলো কোনো নির্দিষ্ট সময় বা স্থানে ০, ১, ২, ৩, ... ইত্যাদি বার ঘটতে পারে) বিভিন্ন ঘটনার ক্ষেত্রে এটি ব্যবহার করা যায় যদি ঐ ঘটনা ঘটার সম্ভাবনা সময় বা স্থানে ধ্রুব হয়। পয়সোঁ মডেল দিয়ে ব্যাখ্যা করা যাবে এমন কিছু উদাহরণ হলো:
- প্রুশিয়ান ঘোড়সওয়ার বাহিনীর প্রতিটি বিভাগে প্রতি বছর ঘোড়ার পদাঘাতে মৃত সৈন্যের সংখ্যা। লাদিসলাউস বরতিকিউইসজ (১৮৬৮-১৯৩১) একটি বইয়ে এই উদাহরণ ব্যবহার করেছেন।
- গিনেস বিয়ার চোলাইয়ের সময় ব্যবহৃত ঈস্ট কোষের সংখ্যা। এই উদাহরণ ব্যবহার করেছিলেন উইলিয়াম সিলি গসেট (১৮৭৬-১৯৩৭)।[২৯]
- এক মিনিটের মধ্যে কোনো কল সেন্টারে আসা কলের সংখ্যা। উদাহরণটির বিবরণ দিয়েছিলেন এ. কে. এরল্যাং।
- ইন্টারনেট ট্র্যাফিক।
- দুটি দলের কোনো খেলায় গোলের সংখ্যা।[৩০]
- কোনো নির্দিষ্ট বয়সসীমার মানুষের মধ্যে প্রতি বছর মৃত্যুর সংখ্যা।
- কোনো নির্দিষ্ট সময়ের মধ্যে শেয়ার বাজারের ঊর্ধ্বগতির সংখ্যা।
- সমধর্মীতা অনুমান সঠিক ধরে নিলে প্রতি মিনিটে একটি ওয়েব সার্ভারে যতবার প্রবেশ করা হয়।
- নির্দিষ্ট পরিমাণ বিকিরণের পরে একটি নির্দিষ্ট পরিমাণ ডিএনএ-তে ঘটা পরিব্যক্তির সংখ্যা।
- সংক্রমণ ঘটানো জীবাণু ও সংক্রমণযোগ্য কোষের হার ধ্রুব থাকলে সংক্রমিত কোষের অনুপাত।
- নির্দিষ্ট পরিমাণ তরলে ব্যাকটেরিয়ার সংখ্যা।[৩১]
- একটি পিক্সেল বর্তনীতে নির্দিষ্ট পরিমাণ আলো ফেললে নির্দিষ্ট সময়ে পৌঁছা ফোটনের সংখ্যা।
- দ্বিতীয় বিশ্বযুদ্ধের সময় লন্ডনের আকাশে ভি-১-ফ্লায়িং বোম্বিং এর পরিমাণ। ১৯৪৬ সালে এ নিয়ে কাজ করেন আর. ডি. ক্লার্ক।[৩২][৩৩]
১৯৭৬ সালে গ্যালাঘার দেখান যে ছোট ব্যাপ্তিতে মৌলিক সংখ্যার পরিমাণ পয়সোঁ বিন্যাস মেনে চলে, যদি হার্ডি ও লিটলউডের একটি অপ্রমাণিত অমুমানের নির্দিষ্ট সংস্করণ সত্য হয়।[৩৪]
দুর্লভ ঘটনার বিধি[সম্পাদনা]

কোনো ঘটনা ঘটার হারের সাথে কোনো একটি ছোট উপব্যাপ্তিতে (স্থান, সময় বা অন্য কিছুর) ঐ ঘটনা ঘটার সম্ভাবনার সাথে সম্পর্ক আছে। পয়সোঁ বিন্যাসের ক্ষেত্রে ধরে নেওয়া হয়, ছোট ছোট এমন অনেকগুলো উপব্যাপ্তি আছে যাতে একটি ঘটনা দুইবার ঘটার সম্ভাবনা নগণ্য। এই অনুমানের সাহায্যে দ্বিপদী বিন্যাস থেকে পয়সোঁ বিন্যাস তৈরি করা যায়। এর জন্য শুধু প্রয়োজন পূর্ণ ব্যাপ্তিতে মোট ঘটনার প্রত্যাশিত মান। ধরা যাক, এই সমষ্টি হলো । সম্পূর্ণ ব্যাপ্তিকে এবার সংখ্যক সমান আকারের উপব্যাপ্তিতে বিভক্ত করা হলো। এরা হলো । এখানে > হতে হবে (আমরা ব্যাপ্তির খুব সামান্য অংশ নিয়ে কাজ করছি বলে এই অনুমান অর্থবহই বটে)। এর অর্থ হলো প্রতিটি এর জন্য কোনো ব্যাপ্তি -এ প্রত্যাশিত ঘটনার সংখ্যা । এবার আমরা ধরে নেব, সম্পূর্ণ ব্যাপ্তিতে কোনো ঘটনার সংঘটন একটি বার্নুলি চেষ্টা, যেখানে তম চেষ্টা হলো উপব্যাপ্তিতে ঘটনা ঘটছে কি না তা দেখা, যার সম্ভাবনা । এমন চেষ্টায় প্রত্যাশিত ঘটনার সংখ্যা হবে , যা সম্পূর্ণ ব্যাপ্তিতে মোট ঘটনার প্রত্যাশিত মান। অতএব ব্যাপ্তির সবগুলো বিভক্ত অংশের জন্য আমরা ঘটনা ঘটাকে আকারের বার্নুলি প্রক্রিয়া দিয়ে আসন্নীকৃত করেছি। আগেও বলা হয়েছে, আমরা খুব ছোট উপব্যাপ্তি নিয়ে কাজ করছি। অতএব আমাদের এর সীমা হবে অসীমের দিকে। এক্ষেত্রে পয়সোঁ সীমা উপপাদ্যের মাধ্যমে দ্বিপদী বিন্যাস পয়সোঁ বিন্যাসের আসন্ন মান প্রদান করবে।
একটি নির্দিষ্ট ডিএনএ এর ক্রমের পরিব্যাপ্তির সংখ্যাসহ উপরের বেশ কিছু উদাহরণে গণনাকৃত ঘটনা প্রকৃতপক্ষে বিচ্ছিন্ন চেষ্টার ফলাফল। ফলে এদেরকে দ্বিপদী বিন্যাস দিয়ে মডেল করলেই বেশি নিখুঁত ফলাফল পাওয়া যাবে। অর্থাৎ,
এক্ষেত্রে n খুব বড় আর p খুব ছোট (ফলে np হবে মাঝামাঝি মানের)। তাহলে বিন্যাসটিকে অপেক্ষাকৃত সহজ উপায়ে পয়সোঁ বিন্যাস দিয়ে আসন্নীকৃত করা যাবে।
এই আসন্নীকরণকে অনেকসময় দুর্লভ ঘটনার বিধি বলা হয়[৩৫], কেননা প্রতিটি আলাদা n বার্নুলি ঘটনা এক একটি দুর্লভ ঘটনা। নামটি কিছুটা বিভ্রান্তিকর, কারণ np ছোট হলে পয়সোঁ প্রক্রিয়ার মোট সফলতার সংখ্যাকে দুর্লভ হতে হবে না। যেমন এক ঘণ্টায় একটি ব্যস্ত সুইচবোর্ডে আসা টেলিফোন কলের সংখ্যা পয়সোঁ বিন্যাস মেনে চলবে। এখানে অপারেটরের কাছে মনে হবে খুব ঘন ঘন কল আসছে। তবে একজন সাধারণ মানুষের কাছে একে দুর্লভ ঘটনা মনে হবে, কারণ ঐ নির্দিষ্ট ঘণ্টায় তিনি ঐ সুইচবোর্ড থেকে কল করবেন তার সম্ভাবনা খুব কম।
অনেক সময় বিধি কথাটিকে সম্ভাবনা বিন্যাসের প্রতিশব্দ হিসেবে ব্যবহার করা হয়। আর বিধির অভিসার বলতে বিন্যাসের অভিসার বোঝানো হয়। এ কারণে পয়সোঁ বিন্যাসকে অনেক সময় ছোট সংখ্যার বিধিও বলা হয়। কারণ এটি দুর্লভ ঘটনার সংখ্যার সম্ভাবনা বিন্যাস যেখানে ঘটনা অনেকভাবে ঘটতে পারে। লাদিসলাউস বরতিকিউইসজ ১৮৯৮ সালে ল অব স্মল নাম্বারস (ছোট সংখ্যার বিধি) নামে পয়সোঁ বিন্যাস নিয়ে একটি বই লিখেছেন।[৩৬]
পয়সোঁ বিন্দু পক্রিয়া[সম্পাদনা]
কোনো সসীম অঞ্চলে অবস্থিত কোনো পয়সোঁ বিন্দু প্রক্রিয়ার বিন্দু সংখ্যা থেকে পয়সোঁ বিন্যাস পাওয়া যায়। আরও নির্দিষ্ট করে বললে, D যদি কোনো স্থান হয়, যেমন ইউক্লিডীয় স্থান Rd, যাতে ক্ষেত্রফল, আয়তন বা আরও সার্বিক দৃষ্টিকোণ থেকে বললে লেবেসগ পরিমাপ |D| সসীম অঞ্চল হয় এবং N(D) দ্বারা D-তে বিন্দুর সংখ্যা বোঝানো হলে
বিজ্ঞানে অন্যান্য প্রয়োগ[সম্পাদনা]
পয়সোঁ প্রক্রিয়ায় পর্যবেক্ষণকৃত ঘটনার সংখ্যা λ থেকে কম-বেশি হয়। আর পরিমিত ব্যবধান হয় । এই কম-বেশি হওয়াকে বলে পয়সোঁ নয়েজ বা (বিশেষ করে ইলেকট্রনিক্সে) শট নয়েজ।
স্বাধীন বিচ্ছিন্ন সংঘটন পরিমাপের ক্ষেত্রে গড় ও পরিমিত ব্যবধানের সংশ্লেষণ বৈজ্ঞানিক দৃষ্টিকোণ থেকে খুব কার্যকর। গড় সঙ্কেতের আশেপাশে কতটা ওঠা-নামা বা স্পন্দন হয় সেটা লক্ষ করে একটিমাত্র ঘটনার প্রভাব পরিমাপ করা যায়, যদিও সেই প্রভাব সরাসরি লক্ষ করার মতো যথেষ্ট বেশি নাও হয়। যেমন তড়িৎ প্রবাহ ও এর শট নয়েজের সংশ্লেষণ কাজে লাগিয়ে একটি ইলেকট্রনের আধান e পরিমাপ করা যায়। কোনো নির্দিষ্ট t সময়ে N সংখ্যক ইলেকট্রন একটি বিন্দুকে অতিক্রম করলে গড় প্রবাহ হবে । যেহেতু প্রবাহের ওঠা-নামা হবে (যা পয়সোঁ প্রক্রিয়ার পরিমিত ব্যবধান) ক্রমের, অতএব আধান অনুপাত থেকে পরিমাপ করা যাবে।
একটি সাধারণ উদাহরণ হলো কোনো আলোকচিত্রকে বড় করা হলে যে কণা-প্রবণতা চোখে পড়ে। এ কণা-প্রবণতার কারণ কণারা নিজেরা নয়, বরং কারণ হলো রূপার কণায় পয়সোঁ স্পন্দন কমে যাওয়া। কণা-প্রবণতা ও প্রসারণের মাত্রার সংশ্লেষণ ব্যবহার করে প্রতিটি কণার প্রভাব পরিমাপ করা সম্ভব (এত ছোট এ প্রভাব খালি চোখে দেখা যায় না)। পয়সোঁ নয়েজের আরও অনেক আণবিক প্রয়োগ আবিষ্কৃত হয়েছে। যেমন, কোষ ঝিল্লিতে গ্রাহক অণুর সংখ্যা ঘনত্ব।
কার্যকারণ সেট তত্ত্বে স্থানকালের বিচ্ছিন্ন উপাদান আয়তনের মধ্যে পয়সোঁ বিন্যাস মেনে চলে।
পয়সোঁ দৈব চলক উৎপাদন[সম্পাদনা]
জনাব নুথ পয়সোঁ বিন্যাস থেকে সংখ্যা উৎপাদনের (ছদ্ম-দৈব সংখ্যা নমুনায়ন) একটি সরল অ্যালগোরিদম প্রদান করেছেন:
algorithm poisson random number (Knuth):
init:
Let L ← e−λ, k ← 0 and p ← 1.
do:
k ← k + 1.
Generate uniform random number u in [0,1] and let p ← p × u.
while p > L.
return k − 1.
প্রাপ্ত মান k এর জটিলতা রৈখিক, যার গড় মান λ। একে আরও উন্নত করে অনেকগুলো অ্যালগোরিদম তৈরি করা হয়েছে।
λ বড় হলে L = e−λ এর মান অনেক বেশি ছোট হয়ে যায়। অ্যালগোরিদমে সামান্য পরিবর্তন এনে এ সমস্যার সমাধান করা যায়। এ জন্য নতুন একটি পরামিতি STEP নিয়ে আসা হয় যাতে e−STEP এর মান আগের মতো ছোট হয়ে যায় না।
algorithm poisson random number (Junhao, based on Knuth):
init:
Let λLeft ← λ, k ← 0 and p ← 1.
do:
k ← k + 1.
Generate uniform random number u in (0,1) and let p ← p × u.
while p < 1 and λLeft > 0:
if λLeft > STEP:
p ← p × eSTEP
λLeft ← λLeft − STEP
else:
p ← p × eλLeft
λLeft ← 0
while p > 1.
return k − 1.
STEP এর মান নির্ভর করে প্রাথমিকভাবে সর্বোচ্চ কত বড় মান বাছাই করা হবে তার ওপর। ডাবল-প্রিসিশন ফ্লোটিং পয়েন্ট ফরম্যাটের ক্ষেত্রে প্রাথমিক মান e700 এর কাছাকাছি। অতএব STEP এর মান ৫০০ নেওয়া নিরাপদ।
λ এর বড় মানের ক্ষেত্রে অন্য সমাধানের মধ্যে রয়েছে প্রত্যাখ্যান নমুনায়ন ও গাউসীয় আসন্নীকরণ।
λ এর ছোট মানের ক্ষেত্রে বিপরীত রূপান্তর নমুনায়ন খুব সরল ও কার্যকর। এক্ষেত্রে প্রতিটি নমুনার জন্য শুধু একটি করে সুষম দৈব সংখ্যা u প্রয়োজন হয়। ক্রমযোজিত সম্ভাবনা u এর বেশি হওয়া পর্যন্ত নেওয়া হতে থাকে।
algorithm Poisson generator based upon the inversion by sequential search:[৩৭] init: Let x ← 0, p ← e−λ, s ← p. Generate uniform random number u in [0,1]. while u > s do: x ← x + 1. p ← p * λ / x. s ← s + p. return x.
পরামিতির পরিমাপ[সম্পাদনা]
সর্বোচ্চ সম্ভাব্যতা[সম্পাদনা]
i = 1, ..., n এর জন্য n সংখ্যক পরিমাপকৃত মান দেওয়া থাকলে আমরা যে পয়সোঁ সমগ্রক থেকে নমুনা নেওয়া হয়েছে তার λ পরামিতির মান পরিমাপ করতে পারব। সর্বোচ্চ সম্ভাব্যতা পরিমাপ হলো [৩৮]
প্রতিটি মানের প্রত্যাশিত মান λ হওয়ায় এই গড়ের প্রত্যাশিত মানও λ। ফলে সর্বোচ্চ সম্ভাব্যতা পরিমাপ λ এর একটি নিরপেক্ষ পরিমাপক হবে। এছাড়াও এটি হবে একটি সূক্ষ্ম পরিমাপক। অর্থাৎ, এর পরিমাপকৃত ভেদাঙ্ক ক্র্যামার-রাও নিম্ন সীমা (CRLB) অর্জন করবে। অতএব, এটি হবে ন্যূনতম ভেদাঙ্কের নিরপেক্ষ পরিমাপ। এছাড়াও দেখানো যাবে যে এর সমষ্টি (এবং নমুনা গড়, কারণ এটি সমষ্টির এক-এক অপেক্ষক) λ এর একটি পূর্ণাঙ্গ ও পর্যাপ্ত পরিসংখ্যা।
পর্যাপ্ততা প্রমাণের জন্য আমরা উৎপাদকায়ন উপপাদ্য ব্যবহার করতে পারি। এজন্য আমরা নমুনার যুক্ত পয়সোঁ বিন্যাসের সম্ভাবনা ভর অপেক্ষককে দুটি অংশ ভাগ করি: একটি অংশ কেবলমাত্র নমুনা এর ওপর নির্ভর করে (যাকে বলা হয়), আর আরেকটি নির্ভর করে λ ও অপেক্ষকের মাধ্যমে নমুনা এর ওপর। অতএব হবে λ এর পর্যাপ্ত পরিসংখ্যা।
এখানে প্রথম পদ শুধু এর ওপর নির্ভর করে। দ্বিতীয় পদ শুধু এর মাধ্যমে নমুনার ওপর নির্ভর করে। অতএব, পর্যাপ্ত।
সম্ভাবনা অপেক্ষককে সর্বোচ্চ মান প্রদানকারী λ এর মান বের করতে আমরা সম্ভাব্যতা অপেক্ষকের অ্যালগোরিদম ব্যবহার করতে পারি:
কে λ এর সাপেক্ষে অন্তরীকরণ করে ০ এর সাথে তুলনা করি:
λ এর জন্য এখান থেকে একটি স্থির বিন্দু পাওয়া যায়
অতএব, ki মানগুলোর গড় হলো λ। স্থির বিন্দুতে L এর দ্বিতীয় অন্তরকের চিহ্ন দেখে জানা যাবে λ কেমন চরম মান।
স্থির বিন্দুতে দ্বিতীয় অন্তরকের মান নির্ণয় করলে হবে:
যা ki মানগুলোর গড়ের বিপরীত সংখ্যার n গুণের ঋণাত্মক সংখ্যা। গড় ধনাত্মক হলে এটি ঋণাত্মক হয়। এই শর্ত পূরণ হলে সম্ভাবনা অপেক্ষক এই স্থির বিন্দুতে সর্বোচ্চ মান প্রদান করে।
অন্য দিকে, একটি বিন্যাস গুচ্ছকে পূর্ণাঙ্গ বলা হয় যদি এবং কেবল যদি সকল এর জন্য থেকে হয়। যদি গুলো সুষম ও স্বাধীন বিন্যাস মেনে চলে, তাহলে । আমাদের কাঙ্ক্ষিত বিন্যাস জানা থাকায় সহজেই দেখায় যায়, এই পরিসংখ্যা পূর্ণাঙ্গ।
এই সমীকরণকে সত্য হতে হলে এর মান ০ হতে হবে। কারণ সমষ্টির সকল ও এর সকল সম্ভাব্য মানের জন্য অন্য কোনো পদই ০ হবে না। অতএব, সকল এর জন্য থেকে । অতএব, পরিসংখ্যাটিকে পূর্ণাঙ্গ হিসেবে প্রমাণ করা গেল।
আস্থা ব্যাপ্তি[সম্পাদনা]
পয়সোঁ ও কাই-বর্গ বিন্যাসের ক্রমযোজিত বিন্যাস অপেক্ষকের সম্পর্কের মাধ্যমে পয়সোঁ বিন্যাসের গড়ের আস্থা ব্যাপ্তি বের করা যায়। কাই-বর্গ বিন্যাসের সাথে আবার গ্যামা বিন্যাসের নিবিড় সম্পর্ক রয়েছে। এটা থেকে একটি বিকল্প প্রকাশও পাওয়া যায়। μ গড় বিশিষ্ট পয়সোঁ বিন্যাসের একটি মান k দেওয়া থাকলে 1 – α আস্থা স্তরে μ এর আস্থা ব্যাপ্তি হবে
অথবা সমতুল্যরূপে,
যেখানে হলো n স্বাধীনতার মাত্রার কাই-বর্গ বিন্যাসের কোয়ান্টাইল অপেক্ষক (p এর নিম্ন প্রান্তে), আর হলো গ্যামা বিন্যাসের কোয়ান্টাইল অপেক্ষক যেখানে আকৃতি পরামিতি n ও মাপনী পরামিতি ১।[১৭]:১৭১[৩৯] এই ব্যাপ্তিটি এই অর্থে প্রকৃত যে এর কাভারেজ সম্ভবনা কখনও 1 – α এর কম হয় না।
গ্যামা বিন্যাসের কোয়ান্টাইল পাওয়া না গেলেও (উইলসন-হিলফেরটি রূপান্তরের ভিত্তিতে) প্রকৃত ব্যাপ্তির একটি নিখুঁত আসন্ন মান প্রস্তাব করা হয়েছে:[৪০]
যেখানে হলো আদর্শ পরিমিত বিন্যাসের মান, যার উর্ধ অংশের ক্ষেত্রফল α / 2।
উপরের মতো একই প্রসঙ্গে (λ গড়ের পয়সোঁ বিন্যাসের n সংখ্যক ki মানের একটি নমুনা দেওয়া থাকলে) এই সূত্রগুলোর প্রয়োগের জন্য নিচের সমীকরণটি কাজে লাগানো হয়:
এখান থেকে μ = nλ এর ব্যাপ্তি হিসেব করে বের করা হয় এবং পরিশেষে λ এর ব্যাপ্তি বের করা হয়।
বায়েসীয় অনুমিতি[সম্পাদনা]
বায়েসীয় অনুমিতিতে পয়সোঁ বিন্যাসের হার পরামিতি λ এর কনজুগেট প্রাইঅর হলো গ্যামা বিন্যাস।[৪১] ধরা যাক
দিয়ে বোঝানো হচ্ছে λ একটি গ্যামা সম্ভাবনা বিন্যাস g মেনে চলছে, যার আকৃতি পরামিতি α ও বিপরীত মাপনী পরামিতি β:
তাহলে আগের মতো n আকারের পরিমাপকৃত ki এর একটি নমুনা ও একটি Gamma(α, β) প্রাইঅর দেওয়া থাকলে পোস্টেরিয়র বা উত্তর হবে:
পোস্টেরিয়র গড় E[λ] সর্বোচ্চ সম্ভাব্যতা পরিমাপ এর কাছাকাছি হবে সীমায়, যা গ্যামা বিন্যাসের গড়ের সাধারণ প্রকাশ থেকে সাথে সাথেই পাওয়া যায়।
একটি বাড়তি মানের জন্য উত্তর পূর্বাভাসমূলক বিন্যাস হবে ঋণাত্মক দ্বিপদী বিন্যাস,[৪২] যাকে অনেকসময় গ্যামা-পয়সোঁ বিন্যাসও বলা হয়।
বহু পয়সোঁ গড়ের যুগপৎ পরিমাপ[সম্পাদনা]
ধরা যাক, হলো সংখ্যক পয়সোঁ বিন্যাসের এক গুচ্ছ স্বাধীন দৈব চলক, যাদের প্রতিটির পরামিতি , যেখানে । আমরা এই পরামিতিগুলো পরিমাপ করতে চাই। ক্লিভেনসন ও জিডেক দেখিয়েছেন যে পরমিতকৃত বর্গ ত্রুটি ক্ষয়ের অধীনে , যেখানে । তাহলে পরিমিত গড়ের ক্ষেত্রে স্টেইনের উদাহরণের মতোই সর্বোচ্চ সম্ভাব্যতা পরিমাপ (MLE) অগ্রহণযোগ্য।[৪৩]
এক্ষেত্রে যে-কোনো ও এর জন্য গুরুলঘু পরিমাপক গুচ্ছ হবে[৪৪]
দ্বিচলক পয়সোঁ বিন্যাস[সম্পাদনা]
এই বিন্যাসটিকে সম্প্রসারিত করে দুটি চলকের জন্যও উপযোগী করা হয়েছে।[৪৫] বিন্যাসটির উৎপাদী অপেক্ষক হলো
যেখানে
প্রান্তিক বিন্যাসগুলো হলো Poisson(θ1) ও Poisson(θ2) এবং সংশ্লেষণাঙ্ক
পরিসরে আবদ্ধ।
দ্বিচলক পয়সোঁ বিন্যাস উৎপাদন করার একটি সরল প্রক্রিয়া হলো তিনটি স্বাধীন পয়সোঁ বিন্যাস নেওয়া, যাদের গড় যথাক্রমে । অতঃপর বসাতে হবে। দ্বিচলক পয়সোঁ বিন্যাসের সম্ভাবনা অপেক্ষক হবে
পয়সোঁ বিন্যাসের জন্য কম্পিউটার সফটওয়্যার[সম্পাদনা]
নিবেদিত সফটওয়্যার লাইব্রেরিগুলো দিয়ে পয়সোঁ বিন্যাসের মূলত দুটি কাজ করা হয়: পয়সোঁ বিন্যাস এর মান নির্ণয় ও এ বিন্যাস থেকে দৈব চলক উৎপাদন।
পয়সোঁ বিন্যাসের মান নির্ণয়[সম্পাদনা]
নির্দিষ্ট ও এর জন্য এর মান সহজেই বের করা যায়। এটা করা হয় সূচকীয়, ঘাত ও ফ্যাক্টোরিয়াল অপেক্ষকের ভিত্তিতে এর আদর্শ সংজ্ঞা কাজে লাগিয়ে। অবশ্য এর বড় মানের ক্ষেত্রে নাকচ হয়ে যাওয়ার ঝুঁকি থেকেই যায়। এ ঝুঁকি এড়াতে আদর্শ লাইব্রেরি math.h এর lgamma ব্যবহার করা যেতে পারে।
কিছু কম্পিউটিং লাইব্রেরিতে সহজাতভাবেই পয়সোঁ বিন্যাস থাকে। যেমন:
- R প্রোগ্রামিং ল্যাংগুয়েজ: ফাংশন
dpois(x, lambda); - এক্সেল: ফাংশন
POISSON( x, mean, cumulative), যাতে ক্রমযোজিত বিন্যাস উল্লেখ করারও ব্যবস্থা আছে; - ম্যাথম্যাটিকা: এক চলকের পয়সোঁ বিন্যাস
PoissonDistribution[],[৪৬] দ্বিচলক পয়সোঁ বিন্যাসMultivariatePoissonDistribution[,{ , }],.[৪৭]
পয়সোঁ বিন্যাস থেকে দৈব চয়ন[সম্পাদনা]
নির্দিষ্ট এর জন্য পয়সোঁ বিন্যাস থেকে দৈব পূর্ণ সংখ্যা উৎপাদন করা আরও সহজ। এ কাজের জন্য আছে:
- জিএনইউ সায়েন্টিফিক লাইব্রেরি (GSL): ফাংশন gsl_ran_poisson
- R প্রোগ্রামিং ল্যাংগুয়েজ: ফাংশন
rpois(n, lambda);
আরও দেখুন[সম্পাদনা]
তথ্যসূত্র[সম্পাদনা]
উদ্ধৃতি[সম্পাদনা]
- ↑ Frank A. Haight (১৯৬৭)। Handbook of the Poisson Distribution। New York: John Wiley & Sons।
- ↑ "Statistics | The Poisson Distribution"। Umass.edu। ২০০৭-০৮-২৪। ২০১৪-০৪-১৯ তারিখে মূল থেকে আর্কাইভ করা। সংগ্রহের তারিখ ২০১৪-০৪-১৮।
- ↑ Ugarte, MD; Militino, AF; Arnholt, AT (২০১৬), Probability and Statistics with R (Second সংস্করণ), CRC Press, আইএসবিএন 978-1-4665-0439-4
- ↑ S.D. Poisson, Probabilité des jugements en matière criminelle et en matière civile, précédées des règles générales du calcul des probabilitiés (Paris, France: Bachelier, 1837), page 206.
- ↑ Stigler, Stephen M. (১৯৮২)। "Poisson on the poisson distribution"। Statistics & Probability Letters। 1: 33–35। ডিওআই:10.1016/0167-7152(82)90010-4।
- ↑ Hald, A.; de Moivre, Abraham; McClintock, Bruce (১৯৮৪)। "A. de Moivre: 'De Mensura Sortis' or 'On the Measurement of Chance'"। International Statistical Review / Revue Internationale de Statistique। 52 (3): 229–262। জেস্টোর 1403045। ডিওআই:10.2307/1403045।
- ↑ Ladislaus von Bortkiewicz, Das Gesetz der kleinen Zahlen [The law of small numbers] (Leipzig, Germany: B.G. Teubner, 1898). On page 1, Bortkiewicz presents the Poisson distribution. On pages 23–25, Bortkiewicz presents his analysis of "4. Beispiel: Die durch Schlag eines Pferdes im preussischen Heere Getöteten." (4. Example: Those killed in the Prussian army by a horse's kick.).
- ↑ Probability and Stochastic Processes: A Friendly Introduction for Electrical and Computer Engineers, Roy D. Yates, David Goodman, page 60.
- ↑ প্রমাণের জন্য দেখুন: Proof wiki: expectation and Proof wiki: variance
- ↑ Some Poisson models, Vose Software, সংগ্রহের তারিখ ২০১৬-০১-১৮
- ↑ Helske, Jouni (২০১৫-০৬-২৫), KFAS: Exponential family state space models in R (পিডিএফ), Comprehensive R Archive Network, arXiv:1612.01907
 , বিবকোড:2016arXiv161201907H, সংগ্রহের তারিখ ২০১৬-০১-১৮
, বিবকোড:2016arXiv161201907H, সংগ্রহের তারিখ ২০১৬-০১-১৮
- ↑ Choi KP (1994) On the medians of Gamma distributions and an equation of Ramanujan. Proc Amer Math Soc 121 (1) 245–251
- ↑ Riordan, John (১৯৩৭)। "Moment recurrence relations for binomial, Poisson and hypergeometric frequency distributions"। Annals of Mathematical Statistics। 8 (2): 103–111। ডিওআই:10.1214/aoms/1177732430। Also see Haight (1967), p. 6.
- ↑ E. L. Lehmann (১৯৮৬)। Testing Statistical Hypotheses (second সংস্করণ)। New York: Springer Verlag। আইএসবিএন 978-0-387-94919-2। page 65.
- ↑ Raikov, D. (1937). On the decomposition of Poisson laws. Comptes Rendus de l'Académie des Sciences de l'URSS, 14, 9–11. (The proof is also given in von Mises, Richard (১৯৬৪)। Mathematical Theory of Probability and Statistics। New York: Academic Press।)
- ↑ Laha, R. G. & Rohatgi, V. K. (১৯৭৯-০৫-০১)। Probability Theory। New York: John Wiley & Sons। পৃষ্ঠা 233। আইএসবিএন 978-0-471-03262-5।
- ↑ ক খ গ Johnson, N. L.; Kotz, S.; Kemp, A. W. (১৯৯৩)। Univariate Discrete distributions (2nd সংস্করণ)। Wiley। আইএসবিএন 0-471-54897-9।
- ↑ Michael Mitzenmacher & Eli Upfal (২০০৫-০১-৩১)। Probability and Computing: Randomized Algorithms and Probabilistic Analysis। Cambridge University Press। পৃষ্ঠা 97। আইএসবিএন 978-0521835404।
- ↑ http://downloads.hindawi.com/archive/2013/412958.pdf
- ↑ "Optimal Haplotype Assembly from High-Throughput Mate-Pair Reads, published in ISIT 2015"
- ↑ NIST/SEMATECH, '6.3.3.1. Counts Control Charts', e-Handbook of Statistical Methods, accessed 25 October 2006
- ↑ Huiming, Zhang; Yunxiao Liu; Bo Li (২০১৪)। "Notes on discrete compound Poisson model with applications to risk theory"। Insurance: Mathematics and Economics। 59: 325–336। ডিওআই:10.1016/j.insmatheco.2014.09.012।
- ↑ Huiming, Zhang; Bo Li (২০১৬)। "Characterizations of discrete compound Poisson distributions"। Communications in Statistics - Theory and Methods। 45 (22): 6789–6802। ডিওআই:10.1080/03610926.2014.901375।
- ↑ McCullagh, Peter; Nelder, John (১৯৮৯)। Generalized Linear Models। London: Chapman and Hall। আইএসবিএন 978-0-412-31760-6। page 196 gives the approximation and higher order terms.
- ↑ S. M. Ross (২০০৭)। Introduction to Probability Models (ninth সংস্করণ)। Boston: Academic Press। আইএসবিএন 978-0-12-598062-3। pp. 307–308.
- ↑ "The Poisson Process as a Model for a Diversity of Behavioural Phenomena"
- ↑ Paul J. Flory (১৯৪০)। "Molecular Size Distribution in Ethylene Oxide Polymers"। Journal of the American Chemical Society। 62 (6): 1561–1565। ডিওআই:10.1021/ja01863a066।
- ↑ Lomnitz, Cinna (১৯৯৪)। Fundamentals of earthquake prediction। New York: John Wiley & Sons। আইএসবিএন 0-471-57419-8। ওসিএলসি 647404423।
- ↑ Philip J. Boland (১৯৮৪)। "A Biographical Glimpse of William Sealy Gosset"। The American Statistician। 38 (3): 179–183। ডিওআই:10.1080/00031305.1984.10483195।
- ↑
Dave Hornby। "Football Prediction Model: Poisson Distribution"।
calculate the probability of outcomes for a football match, which in turn can be turned into odds that we can use to identify value in the market.
- ↑ Koyama, Kento; Hokunan, Hidekazu; Hasegawa, Mayumi; Kawamura, Shuso; Koseki, Shigenobu (২০১৬-১২-০১)। "Do bacterial cell numbers follow a theoretical Poisson distribution? Comparison of experimentally obtained numbers of single cells with random number generation via computer simulation"। Food Microbiology (ইংরেজি ভাষায়)। 60: 49–53। আইএসএসএন 0740-0020। ডিওআই:10.1016/j.fm.2016.05.019।
- ↑ Clarke, R. D. (১৯৪৬)। "An application of the Poisson distribution"। Journal of the Institute of Actuaries। 72 (3): 481। ডিওআই:10.1017/S0020268100035435।
- ↑
Aatish Bhatia (২০১২-১২-২১)। "What does randomness look like?"। Wired।
Within a large area of London, the bombs weren’t being targeted. They rained down at random in a devastating, city-wide game of Russian roulette.
- ↑ Gallagher, P. X. (১৯৭৬)। "On the distribution of primes in short intervals"। Mathematika। 23: 4–9। ডিওআই:10.1112/s0025579300016442।
- ↑ A. Colin Cameron; Pravin K. Trivedi (১৯৯৮)। Regression Analysis of Count Data। আইএসবিএন 9780521635677। সংগ্রহের তারিখ ২০১৩-০১-৩০।
(p.5) The law of rare events states that the total number of events will follow, approximately, the Poisson distribution if an event may occur in any of a large number of trials but the probability of occurrence in any given trial is small.
- ↑ Edgeworth, F. Y. (১৯১৩)। "On the use of the theory of probabilities in statistics relating to society"। Journal of the Royal Statistical Society। 76 (2): 165–193। জেস্টোর 2340091। ডিওআই:10.2307/2340091।
- ↑ Devroye, Luc (১৯৮৬)। "Discrete Univariate Distributions" (পিডিএফ)। Non-Uniform Random Variate Generation। New York: Springer-Verlag। পৃষ্ঠা 505।
- ↑ Paszek, Ewa। "Maximum Likelihood Estimation – Examples"।
- ↑ Garwood, F. (১৯৩৬)। "Fiducial Limits for the Poisson Distribution"। Biometrika। 28 (3/4): 437–442। ডিওআই:10.1093/biomet/28.3-4.437।
- ↑ Breslow, NE; Day, NE (১৯৮৭)। Statistical Methods in Cancer Research: Volume 2—The Design and Analysis of Cohort Studies। Paris: International Agency for Research on Cancer। আইএসবিএন 978-92-832-0182-3। ৮ আগস্ট ২০১৮ তারিখে মূল থেকে আর্কাইভ করা। সংগ্রহের তারিখ ২৩ আগস্ট ২০১৯।
- ↑ Fink, Daniel (১৯৯৭)। A Compendium of Conjugate Priors।
- ↑ Gelman; ও অন্যান্য (২০০৫)। Bayesian Data Analysis (2nd সংস্করণ)। পৃষ্ঠা 60।
- ↑ Clevenson, M. L.; Zidek, J. V. (১৯৭৫)। "Simultaneous Estimation of the Means of Independent Poisson Laws"। Journal of the American Statistical Association। 70 (351a): 698–705। ডিওআই:10.1080/01621459.1975.10482497।
- ↑ Berger, J. O. (১৯৮৫)। Statistical Decision Theory and Bayesian Analysis (2nd সংস্করণ)। Springer। বিবকোড:1985sdtb.book.....B।
- ↑ Loukas, S.; Kemp, C. D. (১৯৮৬)। "The Index of Dispersion Test for the Bivariate Poisson Distribution"। Biometrics। 42 (4): 941–948। জেস্টোর 2530708। ডিওআই:10.2307/2530708।
- ↑ "Wolfram Language: PoissonDistribution reference page"। wolfram.com। সংগ্রহের তারিখ ২০১৬-০৪-০৮।
- ↑ "Wolfram Language: MultivariatePoissonDistribution reference page"। wolfram.com। সংগ্রহের তারিখ ২০১৬-০৪-০৮।
















![{\displaystyle \lambda [1-\log(\lambda )]+e^{-\lambda }\sum _{k=0}^{\infty }{\frac {\lambda ^{k}\log(k!)}{k!}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf6cf37058d59e89453fd5bf9a1ece59a8c81d1a)
































































































































![{\displaystyle g(u,v)=\exp[(\theta _{1}-\theta _{12})(u-1)+(\theta _{2}-\theta _{12})(v-1)+\theta _{12}(uv-1)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0d994b2c4f3b36c80cfd0b97ed72fe289c0855d4)










