বোর মডেল

ইলেকট্রন নির্দিষ্ট পারমাণবিক কক্ষপথে ধনাত্মক নিউক্লিয়াস এর চারপাশে ঘুরতে থাকে এবং যখন ইলেকট্রন এক কক্ষপথ থেকে অন্য কক্ষপথে তার অবস্থান পরিবর্তন করে তখন নির্দিষ্ট পরিমাণ তড়িৎচৌম্বকীয় শক্তি উৎপন্ন হয়। [১]
যে সকল কক্ষপথে ইলেকট্রন প্রদক্ষিণ করতে পারে তাদের কে দেখানো হয়েছে ধূসর বৃত্ত দ্বারা;তাদের ব্যাসার্ধ এমন ভাবে বৃদ্ধি পায় যেন n2, যেখানে n প্রধান কোয়ান্টাম সংখ্যা। এখানে যে পরিবর্তন প্রদর্শিত হয়েছে তা বামার সিরিজ এর প্রথম রেখা উৎপন্ন করে এবং হাইড্রোজেনে এটি ৬৫৬ ন্যানোমিটার তরঙ্গদৈর্ঘ্য বিশিষ্ট ফোটন কণায় পরিণত হয় (লাল রং).]]
পারমাণবিক পদার্থবিদ্যায় সর্বপ্রথম, নীলস বোর, ১৯১৩ সালে পরমাণুর “বোর মডেল” বা রাদারফোর্ড-বোর মডেল উপস্থাপন করেন। তিনি দেখান পরমাণু একটি ধনাত্মক আধানযুক্ত নিউক্লিয়াস এবং তাকে কেন্দ্র করে প্রদক্ষিণরত ইলেকট্রন দ্বারা তৈরি ক্ষুদ্র কণিকা যেখানে ইলেকট্রনগুলো কতগুলি কক্ষপথে নিউক্লিয়াসের চারপাশে সৌরজগতের মতই ঘূর্ণায়মান; কিন্তু মহাকর্ষ বলের পরিবর্তে এখানে ক্রিয়াশীল থাকে স্থির বৈদ্যুতিক বল। ১৯০২ সালে কিউবিক মডেল, ১৯০৪ সালে প্লাম-পুডিং মডেল এবং স্যাটার্নিয়ান মডেল আর ১৯১১ সালে রাদারফোর্ড মডেল এর পরবর্তীতে ১৯১৩ সালে বোর তার এ মডেল উপস্থাপন করেন। রাদারফোর্ড মডেলের উন্নতি সাধনের মাধ্যমে এবং কোয়ান্টাম পদার্থবিদ্যা সমন্বয়ে তিনি এ তত্ত্ব দেন। পরবর্তীতে বোর মডেল বাতিল করা হলেও কোয়ান্টাম তত্ত্ব টিকে থাকে।
এই মডেলের সার্থকতা হল এটি হাইড্রোজেন পরমাণুর বর্ণালি, রাইডবার্গ সূত্র দ্বারা প্রমাণ করতে সক্ষম হয়। রাইডবার্গ সূত্র পরীক্ষামূলকভাবে পরিচিত থাকলেও তাত্ত্বিকভাবে এটি বোর মডেল প্রকাশের পূর্বে সফলতা অর্জন করে নি। বোর মডেল শুধুমাত্র রাইডবার্গ সূত্রের গঠনের-ই ব্যখ্যা করে না, বিভিন্ন ধ্রুবকের সাপেক্ষে এর পরিবর্তনেরও ব্যাখ্যা করে।
উৎস[সম্পাদনা]
বিংশ শতাব্দীর প্রথমভাগে আর্নেস্ট রাদারফোর্ড এর পরীক্ষার মাধ্যমে এটি পরীক্ষিত যে পরমাণু মূলত ঋণাত্মক আধানযুক্ত ইলেক্ট্রন পরিবেষ্টিত ক্ষুদ্রাকার, ঘন, ধনাত্মক আধানযুক্ত একটি নিউক্লিয়াস।[২] এ পরীক্ষিত উপাত্তের উপর ভিত্তি করে রাদারফোর্ড ১৯১১ সালে ইলেকট্রনের কক্ষপথে ঘূর্ণায়মান পরমাণু মডেল উপস্থাপন করেন। তিনি এ মডেল কে সৌরজগতের সাথে তুলনা করেন, কিন্তু এ তুলনার কিছু ত্রুটি থেকে যায়। শাস্ত্রীয় বলবিজ্ঞানের সূত্রমতে (লার্মর সূত্র), নিউক্লিয়াসকে প্রদক্ষিণকালে ইলেকট্রন তড়িৎ-চৌম্বকীয় বিকিরণ করতে থাকবে আর ক্রমাগত শক্তি হারানোর কারণে ইলেকট্রন একটি সর্পিল পথে ১৬ পিকোসেকেন্ডে নিউক্লিয়াসে পতিত হবে।[৩] এটি একটি বৈপ্লবিক মডেল, কারণ এটি দেখায় যে প্রত্যেক পরমাণুই পরিবর্তনশীল।[৪]
এছাড়া, যেহেতু সর্পিল পথে কেন্দ্রমুখী গমনের কারণে ভ্রমনের কক্ষপথ প্রতিনিয়ত ছোট হতে থাকে, বিকিরণের কম্পাঙ্ক প্রতিনিয়ত বাড়তে থাকবে । অর্থাৎ এটি তড়িৎচুম্বকীয় বিকিরণের কম্পাঙ্কে পরিবর্তন আনে। ১৯ শতকের শেষভাগে ইলেকট্রিক ডিসচার্জ নিয়ে আরও গবেষণায় দেখা যায় যে পরমাণু একটি নির্দিষ্ট কম্পাঙ্কের আলো বিকিরণ করে (যা তড়িৎচুম্বকীয় বিকিরণ)।
এ সকল সমস্যার সমাধানের জন্য ১৯১৩ সালে নীল্স বোর তার বোর-মডেল উপস্থাপন করেন। তিনি বলেন যে, ইলেকট্রনের পরিভ্রমণের কতগুলো নির্দিষ্ট নিয়ম থাকবেঃ
- পরমাণুতে ইলেক্ট্রন নিউক্লিয়াসকে কেন্দ্র করে প্রদক্ষিণ করবে।
- নির্দিষ্ট কক্ষপথে অবস্থানকালে এরা স্থিতিশীল থাকবে, কোন বিকিরণ করবে না। বোর এদেরকে "stationary orbits" বা নিশ্চল কক্ষপথ [৫])হিসেবে আখ্যায়িত করেন এসকল কক্ষপথের নিজস্ব শক্তি বর্তমান। এদেরকে শক্তিশেল বা শক্তিস্তর বলা হয়। এসকল শক্তিস্তরে পরিভ্রমণকালে ইলেকট্রন কোন প্রকার শক্তি অর্জন বা বিকিরণ করে না। পরমাণুর বোর-মডেলের ভিত্তি মূলত, বিকিরণ সম্পর্কিত প্ল্যাঙ্কের কোয়ান্টাম তত্ব।
- এক কক্ষপথ থেকে অন্য কক্ষপথে অবস্থান পরিবর্তনকালে ইলেকট্রন নির্দিষ্ট পরিমাণ শক্তি অর্জন বা বিকিরণ করে যা ওই দুই কক্ষপথের শক্তির পার্থক্য “v” এর সমান। প্ল্যাঙ্কের সম্পর্ক থেকে,
যেখানে h হল প্ল্যাঙ্কের ধ্রুবক। কোন নির্দিষ্ট সময় “T” এর মাঝে তড়িতবিকিরণের কম্পাঙ্কের পরিবর্তন হবে শাস্ত্রীয় বলবিদ্যা আনুসারে
বোর-মডেলের তাৎপর্য এই যে, এখানে ইলেকট্রন কতগুলো কোয়ান্টাম সূত্রমতে শাস্ত্রীয় বলবিদ্যা অনুসারে নিউক্লিয়াসের চারপাশে ঘুরতে থাকে। যদিও ৩ নং সুত্র উপশক্তিস্তরের সঠিক ধারণা দিতে সক্ষম নয়, বোর ৩ নং সূত্রের সাহায্যে দুই শক্তিস্তরের শক্তির পার্থক্য ব্যখ্যা করেন এবং একটি কোয়ান্টাম সূত্রের অবতারণা করেন যে, কৌণিক ভরবেগ “L” হবে কোন নির্দিষ্ট সংখ্যার পূর্ণগুণিতক।
যেখানে n = 1, 2, 3, ... হচ্ছে প্রধান কোয়ান্টাম সংখ্যা, এবং ħ = h/2π। n এর সর্বনিম্ন মান ১;ফলে সবচে ছোট কক্ষপথের ব্যাসার্ধ হয় ০.০৫২৯ ন্যানোমিটার যা বোর ব্যাসার্ধ নামে পরিচিত। যখন একটি ইলেকট্রন এই সর্বনিম্ন কক্ষপথে অবস্থান করে, এটি নিউক্লিয়াসের কাছাকাছি আর যেতে পারে না। কৌণিক ভরবেগের কোয়ান্টাম নীতি থেকে বোর Bohr[২] হাইড্রোজেন পরমাণু ও অন্যান্য হাইড্রোজেন-সম পরমাণু ও আয়নের নির্দিষ্ট কক্ষপথের শক্তি নির্ণয় করতে সক্ষম হন।
১৯২৪ সালে দে ব্রগলির স্থিরতরঙ্গ তত্ত্ব মূলত, বোর প্রদত্ত সূত্র, কৌণিক ভরবেগ, ħ এর পূর্ণ গুণিতক এর পুনরায় প্রতিফলন ঘটায়ঃ ইলেক্ট্রনকে দেখানো হয় একটি তরঙ্গ হিসেবে যার সম্পূর্ণ তরঙ্গদৈর্ঘ্য তার কক্ষপথের পরিধির অভ্যন্তরে থাকবে
দে ব্রগলির তরঙ্গদৈর্ঘ্য, λ = h/p কে পরিবর্তন করলে বোরের নীতি পাওয়া যায়। ১৯১৩ সালে বোর তার নীতি কে তৎকালীন নিয়মের সাহায্যে প্রমাণ করলেও এর তরঙ্গের ব্যাপারে কোন ধারণা দেন নি। ১৯১৩ সালে ইলেকট্রন বা এরকম বস্তুর তরঙ্গধর্ম উত্থাপিত হয় নি।
১৯২৫ সালে কোয়ান্টাম বলবিদ্যা উপস্থাপিত হউ যেখানে কোয়ান্টাইজ্ড কক্ষপথে ইলেকট্রনের বিচরণের বোর-মডেল কে ইলেকট্রনের গতিপথের আরও সঠিক মডেলে রূপান্তর করা হয়। এই নতুন তত্ব উত্থাপন করেন ওয়ার্নার হাইজেনবার্গ। আস্ট্রেলিয়ান পদার্থবিদ আরউইন শ্রুডিঙ্গার একই তত্বের ভিন্ন রুপ, তরঙ্গ তত্ত্ব স্বাধীনভাবে এবং ভিন্ন যুক্তি দিয়ে উত্থাপন করেন। তিনি দে ব্রগলির পদার্থের তরঙ্গকে ব্যবহার করে একটি ত্রি-মাত্রিক সমীকরণের সমাধান খুঁজছিলেন যা হাইড্রোজেন-সম পরমাণুর নিউক্লিয়াসের ধনাত্মক আধানের প্রভাবে ঘূর্ণায়মান ইলেকট্রন সমূহ কে ব্যাখ্যা করে।
ইলেকট্রনের শক্তিস্তর[সম্পাদনা]
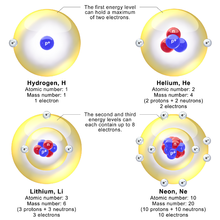
আলো থেকে অনেক কম গতিসম্পন্ন এবং পরস্পরকে প্রদক্ষিণরত দুটি চার্জিত কণার ক্ষেত্রে বোর-মডেল প্রায় সঠিক ফলাফল দিতে পারে। শুধুমাত্র হাইড্রোজেন পরমাণুর মত একক-ইলেক্ট্রন বিশিষ্ট পরমাণু কিংবা একক আয়নযুক্ত হিলিয়াম বা দ্বিত্ব-আয়নযুক্ত লিথিয়াম ছাড়াও পসিট্রনিয়াম ও যেকোনো পরমাণুর রাইডবার্গ অবস্থার ক্ষেত্রেও এটি প্রযোজ্য যেখানে একটি ইলেক্ট্রন অন্য যে কোন কিছুর থেকে অনেক দূরে অবস্থিত। কে-লাইন হতে এক্স-রে রুপান্তরের গণনায় একে ব্যবহার করা যায় যদি অন্যান্য ধারনাগুলো সংযোগ করা হয়(দেখুন, মোসলের নীতি)। উচ্চ শক্তি পদার্থবিদ্যায় হেভি কোয়ার্ক মেসন এর ভর নির্নয়ে একে ব্যবহার করা যায়।
কক্ষপথের গণনায় দুইটি অনুমানের প্রয়োজন।
- চিরায়ত বলবিজ্ঞান
- স্থিরবৈদ্যুতিক আকর্ষণ বলের কারণে ইলেক্ট্রন একটি বৃত্তাকার কক্ষপথে আবদ্ধ থাকে। ইলেকট্রনের কেন্দ্রমুখী বল হয় কুলম্ব বল এর সমান।
- যেখানে me হল ইলেকট্রন এর ভর, e ইলেক্ট্রনের চার্জ, ke হচ্ছে কুলম্বের ধ্রুবক এবং Z হল পরমাণুর পারমাণবিক সংখ্যা।
এখানে ধারণা করা হয় যে, নিউক্লিয়াসের ভর ইলেক্ট্রনের ভর অপেক্ষা অনেক বেশি। এই সমীকরণ যেকোন ব্যাসার্ধে ইলেকট্রনের গতি নির্ণয় করেঃ
- এটি নির্দিষ্ট ব্যাসার্ধে ইলেকট্রনের মোট শক্তিও প্রকাশ করেঃ
- মোট শক্তি ঋণাত্বক এবং r এর ব্যাস্তানুপাতিক। তার মানে ইলেকট্রন কে তার কক্ষপথে পরিভ্রমণকালে প্রোটন থেকে দূরে সরাতে হলে শক্তি প্রয়োজন। r এর অসীম মানের জন্য শক্তির পরিমাণ শূন্য, যা প্রোটন হতে অসীম দূরত্বে অবস্থিত ইলেকট্রনকে বোঝায়। এখানে মোট শক্তি বিভব শক্তি এর অর্ধেক যা অবৃত্তাকার কক্ষপথের জন্য ভিরিয়াল উপপাদ্য দ্বারা প্রমাণিত।
• কোয়ান্টাম নীতি
- কৌণিক ভরবেগ L = mevr হবে ħ এর পূর্ণগুণিতকঃ
- গতিসূত্রকে পরিবর্তন করে n এর সাপেক্ষে r এর জন্য একটি সমীকরণ পাওয়া যায়:
- তাই যেকোন n এ নির্দিষ্ট কক্ষপথের ব্যাসার্ধ হবেঃ
- হাইড্রোজেন পরমাণুর ক্ষেত্রে r এর সর্বনিম্ন মানকে বলা হয় বোর ব্যাসার্ধ যা
- যেকোনো পরমাণুর “n”-তম কক্ষপথের শক্তি নির্ধারিত হয় কক্ষপথের ব্যাসার্ধ ও কোয়ান্টাম সংখ্যা দ্বারাঃ
হাইড্রোজেন পরমাণুর সর্বনিম্ন কক্ষপথে (n = 1) অবস্থিত ইলেকট্রনের শক্তি নিউক্লিয়াস হতে অসীম দূরত্বে অবস্থিত নিশ্চল ইলেকট্রনের তুলনায় প্রায় ১৩.৬ eV কম। পরবর্তী শক্তিস্তরের (n = 2) ক্ষেত্রে এর মান -৩.৪ eV, এবং এর পরের শক্তিস্তরের (n = 3) ক্ষেত্রে এর মান হয় -১.৫১ eV। “n” এর বৃহত্তর মানের জন্য এটি হচ্ছে, বড় কক্ষপথে ঘূর্ণায়মান একটি ইলেকট্রন সম্পন্ন উত্তেজিত পরমাণু সমূহের বন্ধন শক্তি।
শক্তির এ সূত্রে ব্যবহৃত সাধারণ ধ্রুবকগুলোর এ সমাহার কে বলা হয় রাইডবার্গ এনার্জি (RE):
এই অভিব্যক্তি যাচাইকৃত হয় আরও সমন্বয়ের মাধ্যমে যা আরও সাধারণ একক গঠন করেঃ
- হল ইলেকট্রনের অবশিষ্ট ভরশক্তি (৫১১ keV)
- হল সূক্ষ্ম গঠন ধ্রুবক
যেহেতু নিউক্লিয়াসের চারপাশে একটি ইলেকট্রন ঘূর্ণায়মান (এই তত্ত্বের ক্ষেত্রে), সেহেতু ইলেকট্রনের চার্জ q = Z e (যেখানে, “Z” হচ্ছো পারমাণবিক সংখ্যা)হলে আমরা হাইড্রোজেন-সম পরমাণুর শক্তিস্তরের আসল মাত্রার একটি গড়পড়তা ধারণা পাওয়া যায়। তাই “Z” প্রোটন সমৃদ্ধ নিউক্লিয়াসের ক্ষেত্রে শক্তিস্তর হবে (গড়পড়তা হিসাব) :
একটির অধিক ইলেকট্রনের ক্ষেত্রে শক্তিস্তরগুলোকে সঠিকভাবে বিশ্লেষণ করা সম্ভব নয় কারণ এক্ষেত্রে ইলেকট্রনগুলো শুধুমাত্র নিউক্লিয়াস দ্বারাই আকৃষ্ট হয় না, কুলম্ব বল এর কারণে পরস্পর পরস্পরের উপর প্রভাব ফেলে।
বোর নীতি ইলেকট্রনের ভরের পরিবর্তে এর হ্রাসকৃত ভর কে সঠিক ভাবে ব্যবহার করেঃ । এ সংখ্যাগুলো প্রায় সমান কারণ ইলেকট্রনের তুলনার প্রোটনের ভর প্রায় ১৮৩৬.১ গুণ বেশি। এই ব্যাপারটি ঐতিহাসিক ভাবে গুরুত্বপূর্ণ কারণ এটি রাদারফোর্ড কে বোর মডেলের গুরুত্ব বুঝতে সাহায্য করে। এটি ব্যখ্যা করে যে একক-আয়নিত হিলিয়ামের স্পেক্ট্রামে উৎপন্ন রেখা হাইড্রোজেনের ৪ নং ফ্যাক্টরের স্পেক্ট্রামে উৎপন্ন রেখা মূলত একই রকম।
পজিট্রনিয়ামের জন্যও সূত্রটি হ্রাসকৃত ভর ব্যবহার করে, কিন্তু এক্ষেত্রে এটি হয় ইলেকট্রনের ভরের দ্বি-গুণ। এই ব্যাসার্ধের যেকোনো মানের জন্য ইলেকট্রন এবং পজিট্রন উভয়েই তাদের সাধারণ গতির অর্ধেক গতিতে তাদের সাধারণ ভরকেন্দ্রকে প্রদক্ষিণ করতে থাকে। এ সময় গতিশক্তি থাকে সাধারণ গতিশক্তির এক-চতুর্থাংশ। মোট গতিশক্তি হবে একটি ভারী নিউক্লিয়াসকে কেন্দ্র করে ঘূর্ণায়মান একটি ইলেকট্রনের গতিশক্তির অর্ধেক।
- (পজিট্রনিয়াম)
রাইডবার্গ সূত্র[সম্পাদনা]
বোরের তত্ত্বে, ইলেকট্রনের এক শক্তিস্তর থেকে অন্য স্তরে অবস্থান্তর বা কোয়ান্টাম লাফ এর ফলে উদ্ভূত শক্তির পরিবর্তন কে ব্যখ্যা করতে রাইডবার্গ সূত্র ব্যবহার করা হয়। এ সূত্র এর আগেও পরিচিত ছিল। বোরের সূত্র, ইলেকট্রনের চার্জ ও প্ল্যাঙ্কের ধ্রুবক এর মতো আরও কয়টি মৌলিক ধ্রুবকের সাহায্যে, ইতোমধ্যেই জানা এবং পরিমাপকৃত রাইডবার্গ ধ্রুবক এর সংখ্যাতত্ত্বীয় মান দেয়।
যখন ইলেকট্রনকে তার অবস্থান থেকে উচ্চতর স্তরে নিয়ে যাওয়া হয়, এটি তার নিজের স্তরে ফিরে আসার আগ পর্যন্ত সকল স্তরে লাফ দিয়ে যায়, যার ফলে একটি ফোটন নিঃসরণ হয়। হাইড্রোজেনের বিভিন্ন শক্তিস্তরের সূত্র থেকে হাইড্রোজেনের বিকীর্ণ আলোর তরঙ্গদৈর্ঘ্য পাওয়া যায়।
হাইড্রোজেনের দুইটি শক্তিস্তরের শক্তির পার্থক্য থেকে হাইড্রোজেন পরমাণু হতে নিঃসৃত ফোটন কণার শক্তি নির্ণয় করা যায়ঃ
যেখানে nf হল সর্বশেষ শক্তিস্তর, এবং ni হল সর্বপ্রথম শক্তিস্তর.
যেহেতু ফোটন এর শক্তি হল,
নিঃসৃত ফোটনের তরঙ্গদৈর্ঘ্য হবে,
এটি রাইডবার্গ সূত্র নামে পরিচিত, এবং রাইডবার্গ ধ্রুবক R হল সাধারন একক এ , বা । এই তত্ত্ব ১৯ শতকের স্পেক্ট্রোস্কোপি নিয়ে গবেষণারত বিজ্ঞানীদের কাছে পরিচিত ছিল, কিন্তু বোরের পূর্বে এর কোন তাত্ত্বিক ব্যখ্যা কিংবা R এর মান সংক্রান্ত কোন তাত্ত্বিক ধারণা কেউ দেন নি। বিভিন্ন স্পেক্ট্রাল রেখা যেমন লাইম্যান (), বামার (), পাশ্চেন () এর উপর পরীক্ষামূলক পর্যবেক্ষণের উপর ভিত্তি করে বোর সূত্র গঠিত হয়। তখনও পর্যন্ত অন্য রেখাগুলো পর্যবেক্ষণ করা হয় নি বলে বোরের মডেল সাথে সাথে গ্রহণ করা হয়।
একের অধিক ইলেক্ট্রন সম্পন্ন পরমাণুর ক্ষেত্রে, রাইডবার্গ সূত্রের পরিবর্তন করা যায় "Z" এর স্থানে "Z − b" অথবা "n" এর স্থানে "n − b" বসিয়ে, যেখানে b একটি ধ্রুবক যা অন্তর্গত-শেল ও অন্যান্য ইলেকট্রনের প্রভাবে স্ক্রিনিং ইফেক্ট কে প্রদর্শন করে। বোর তার মডেল উপস্থাপনের পূর্বে এটি প্রায়োগিকভাবে প্রতিষ্ঠিত ছিল।
তথ্যসূত্র[সম্পাদনা]
- ↑ Akhlesh Lakhtakia (Ed.); Salpeter, Edwin E. (১৯৯৬)। "Models and Modelers of Hydrogen"। American Journal of Physics। World Scientific। 65 (9): 933। আইএসবিএন 981-02-2302-1। ডিওআই:10.1119/1.18691। বিবকোড:1997AmJPh..65..933L।
- ↑ ক খ Niels Bohr (১৯১৩)। "On the Constitution of Atoms and Molecules, Part I" (পিডিএফ)। Philosophical Magazine। 26 (151): 1–24। ডিওআই:10.1080/14786441308634955।
- ↑ "Olsen and McDonald 2005" (পিডিএফ)। ৯ সেপ্টেম্বর ২০১৯ তারিখে মূল (পিডিএফ) থেকে আর্কাইভ করা। সংগ্রহের তারিখ ২২ ডিসেম্বর ২০১৪।
- ↑ "CK12 – Chemistry Flexbook Second Edition – The Bohr Model of the Atom"। সংগ্রহের তারিখ ৩০ সেপ্টেম্বর ২০১৪।
- ↑ Niels Bohr (১৯১৩)। "On the Constitution of Atoms and Molecules, Part II Systems Containing Only a Single Nucleus" (পিডিএফ)। Philosophical Magazine। 26 (153): 476–502। ডিওআই:10.1080/14786441308634993।
আরো পড়ুন[সম্পাদনা]
- Niels Bohr (১৯১৩)। "On the Constitution of Atoms and Molecules, Part I" (পিডিএফ)। Philosophical Magazine। 26 (151): 1–24। ডিওআই:10.1080/14786441308634955।
- Niels Bohr (১৯১৩)। "On the Constitution of Atoms and Molecules, Part II Systems Containing Only a Single Nucleus" (পিডিএফ)। Philosophical Magazine। 26 (153): 476–502। ডিওআই:10.1080/14786441308634993।
- Niels Bohr (১৯১৩)। "On the Constitution of Atoms and Molecules, Part III Systems containing several nuclei"। Philosophical Magazine। 26: 857–875। ডিওআই:10.1080/14786441308635031।
- Niels Bohr (১৯১৪)। "The spectra of helium and hydrogen"। Nature। 92 (2295): 231–232। ডিওআই:10.1038/092231d0। বিবকোড:1913Natur..92..231B।
- Niels Bohr (১৯২১)। "Atomic Structure"। Nature। 107 (2682): 104–107। ডিওআই:10.1038/107104a0। বিবকোড:1921Natur.107..104B।
- A. Einstein (১৯১৭)। "Zum Quantensatz von Sommerfeld und Epstein"। Verhandlungen der Deutschen Physikalischen Gesellschaft। 19: 82–92। Reprinted in The Collected Papers of Albert Einstein, A. Engel translator, (1997) Princeton University Press, Princeton. 6 p. 434. (provides an elegant reformulation of the Bohr–Sommerfeld quantization conditions, as well as an important insight into the quantization of non-integrable (chaotic) dynamical systems.)
- Linus Carl Pauling (১৯৭০)। "Chapter 5-1"। General Chemistry (3rd সংস্করণ)। San Francisco: W.H. Freeman & Co।
- Reprint: Linus Pauling (১৯৮৮)। General Chemistry। New York: Dover Publications। আইএসবিএন 0-486-65622-5।
- George Gamow (১৯৮৫)। "Chapter 2"। Thirty Years That Shook Physics। Dover Publications।
- Walter J. Lehmann (১৯৭২)। "Chapter 18"। Atomic and Molecular Structure: the development of our concepts। John Wiley and Sons।
- Paul Tipler and Ralph Llewellyn (২০০২)। Modern Physics (4th সংস্করণ)। W. H. Freeman। আইএসবিএন 0-7167-4345-0।
- Klaus Hentschel: Elektronenbahnen, Quantensprünge und Spektren, in: Charlotte Bigg & Jochen Hennig (eds.) Atombilder. Ikonografien des Atoms in Wissenschaft und Öffentlichkeit des 20. Jahrhunderts, Göttingen: Wallstein-Verlag 2009, pp. 51–61
- Steven and Susan Zumdahl (২০১০)। "Chapter 7.4"। Chemistry (8th সংস্করণ)। Brooks/Cole। আইএসবিএন 978-0-495-82992-8।
- Helge Kragh (২০১১)। "Conceptual objections to the Bohr atomic theory — do electrons have a "free will" ?"। European Physical Journal H। 36 (3): 327। ডিওআই:10.1140/epjh/e2011-20031-x। বিবকোড:2011EPJH...36..327K।



























