গণিতে , বিপরীত ত্রিকোণমিতিক ফাংশন (কখনো কখনো আর্কাস ফাংশন , প্রতি-ত্রিকোণমিতিক ফাংশন বা সাইক্লোমেট্রিক ফাংশনও বলা হয়) হলো ত্রিকোণমিতিক ফাংশনসমূহের বিপরীত ফাংশন (উপযুক্তভাবে সীমাবদ্ধ ডোমেন সহ)। বিশেষভাবে, এগুলো সাইন , কোসাইন , ট্যানজেন্ট , কোট্যানজেন্ট , সেক্যান্ট এবং কোসেক্যান্ট ফাংশনের বিপরীত ফাংশন, [১] প্রকৌশলবিদ্যা , নেভিগেশন , পদার্থবিজ্ঞান এবং জ্যামিতিতে ব্যবহৃত হয়।
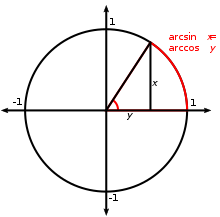
একক ব্যাসার্ধের বৃত্তের জন্য, arcsin এবং arccos হলো প্রকৃত বৃত্তচাপের দৈর্ঘ্য যা প্রদত্ত রাশি দ্বারা নির্ধারিত হয়। বিপরীত ত্রিকোণমিতিক ফাংশনের জন্য বেশ কয়েকটি নোটেশন বিদ্যমান। সবচেয়ে প্রচলিত রীতি হলো arc-উপসর্গ ব্যবহার করে বিপরীত ত্রিকোণমিতিক ফাংশনগুলোর নাম দেওয়া, যেমন: arcsin(x ) , arccos(x ) , arctan(x ) । এটি নিম্নোক্ত জ্যামিতিক সম্পর্ক থেকে আসে:
কোনো বৃত্তচাপ বৃত্তের কেন্দ্রে θ রেডিয়ান কোণ উৎপন্ন করলে বৃত্তচাপ -এর দৈর্ঘ্য rθ , যেখানে r হলো বৃত্তের ব্যাসার্ধ। তাই বলা যায়, কোণ বৃত্তচাপের সমানুপাতিক।
এভাবে একক বৃত্তের ক্ষেত্রে, "যে বৃত্তচাপের কোসাইন হলো x " এবং "যে কোণের কোসাইন হলো x " একই অর্থ প্রকাশ করে, কারণ বৃত্তের ব্যাসার্ধের সমান বৃত্তচাপের দৈর্ঘ্য রেডিয়ানে কোণের পরিমাপের সমান। কম্পিউটার প্রোগ্রামিং ভাষায়, বিপরীত ত্রিকোণমিতিক ফাংশনগুলোকে প্রায়শই asin , acos , atan ইত্যাদি সংক্ষিপ্ত রূপ দ্বারা প্রকাশ করা হয়। [২]
sin−1 (x ) , cos−1 (x ) , tan−1 (x ) , ইত্যাদি -এই নোটেশন ১৮১৩ সালে জন হার্শেল প্রবর্তন করেছিলেন (যা বেশিরভাগ ইংরেজি ভাষার বই ও ওয়েবসাইটগুলোতে ব্যবহৃত হয়)। এটি পুনরাবৃত্ত ফাংশন হিসেবে sin[−1] (x ) , cos[−1] (x ) , tan[−1] (x ) এই নোটেশনের তুলনায় বেশি ব্যবহৃত হয়, যা বিপরীত ফাংশনের নোটেশনের সাথে সামঞ্জস্যপূর্ণ। ফলে এটি প্রতিটি বিপরীত ত্রিকোণমিতিক ফাংশনের মাল্টিভ্যালুয়েড ফাংশন সংজ্ঞায়িত করতে খুবই উপযোগী। উদাহরণস্বরূপ:
tan
−
1
(
x
)
=
{
arctan
(
x
)
+
π
k
∣
k
∈
Z
}
.
{\displaystyle \tan ^{-1}(x)=\{\arctan(x)+\pi k\mid k\in \mathbb {Z} \}~.}
sin2 (x ) (যদিও বন্ধনী ব্যতীত শুধুমাত্র sin2 x এর ব্যবহার খুবই সাধারণ) এর মত অভিব্যক্তির জন্য সাধারণ শব্দার্থবিদ্যার সাথে যৌক্তিকভাবে বিরোধ দেখা দিতে পারে, যা ফাংশন গঠনের পরিবর্তে সংখ্যাগত ঘাতকে নির্দেশ করে এবং ফলস্বরূপ বিপ্রতীক ( গৌণিক বিপরীত ) এবং বিপরীত ফাংশনের জন্য ব্যবহৃত নোটেশনের মধ্যে বিভ্রান্তি সৃষ্টি হতে পারে। [৩]
তবে বিভ্রান্তি কিছুটা প্রশমিত হয় এই কারণে যে প্রতিটি বিপ্রতীক ত্রিকোণমিতিক ফাংশনের নিজস্ব নাম রয়েছে — উদাহরণস্বরূপ, (cos(x ))−1 = sec(x ) । তবুও, কিছু লেখক এটি ব্যবহার না করার পরামর্শ দেন, যেহেতু এটি অস্পষ্ট। এছাড়াও অল্প সংখ্যক লেখকের ব্যবহৃত আরেকটি অস্পষ্ট নিয়ম হলো প্রথমে একটি বড় হাতের অক্ষর ব্যবহার করা এবং সাথে একটি “ −1 ” সুপারস্ক্রিপ্ট থাকে, যেমন: Sin−1 (x ) , Cos−1 (x ) , Tan−1 (x ) , ইত্যাদি। যদিও এটি বিপ্রতীক-এর সাথে বিভ্রান্তি এড়ানোর উদ্দেশ্যে করা হয়েছে, যা sin−1 (x ) , cos−1 (x ) ইত্যাদি দ্বারা প্রকাশ করা উচিত অথবা, আরও ভালোভাবে, sin−1 x , cos−1 x ইত্যাদি দ্বারা। তবে এর পরিবর্তে এটি অস্পষ্টতার আরেকটি প্রধান উৎস তৈরি করে, বিশেষ করে যেহেতু অনেক জনপ্রিয় উচ্চ-স্তরের প্রোগ্রামিং ভাষা (যেমন ম্যাথমেটিকা এবং MAGMA ) আদর্শ ত্রিকোণমিতিক ফাংশনগুলোর জন্য এগুলোর মতো একইরকম বড় হাতের নোটেশন ব্যবহার করে, যেখানে অন্যরা ( Python , SymPy, NumPy , Matlab , MAPLE, ইত্যাদি) ছোট হাতের বর্ণ ব্যবহার করে প্রকাশ করে।
এজন্য, ২০০৯ সাল থেকে আইএসও ৮০০০০-২ স্ট্যান্ডার্ড অনুযায়ী বিপরীত ত্রিকোণমিতিক ফাংশনের জন্য শুধুমাত্র "arc" উপসর্গ নির্দিষ্ট করে দেওয়া হয়েছে। যদিও বাংলাদেশের কলেজ পর্যায়ের বইগুলোতে বিপরীত ফাংশনের অনুরূপ নোটেশনটি বেশি ব্যবহার করা হয়।
নাম
ব্যবহারিক চিহ্ন
সংজ্ঞা
ডোমেইন
রেঞ্জ রেডিয়ান )
রেঞ্জ ডিগ্রি )
arcsine
y
=
arcsin
(
x
)
{\displaystyle y=\arcsin(x)}
x = sin (y )
−
1
≤
x
≤
1
{\displaystyle -1\leq x\leq 1}
−
π
2
≤
y
≤
π
2
{\displaystyle -{\frac {\pi }{2}}\leq y\leq {\frac {\pi }{2}}}
−
90
∘
≤
y
≤
90
∘
{\displaystyle -90^{\circ }\leq y\leq 90^{\circ }}
arccosine
y
=
arccos
(
x
)
{\displaystyle y=\arccos(x)}
x = cos (y )
−
1
≤
x
≤
1
{\displaystyle -1\leq x\leq 1}
0
≤
y
≤
π
{\displaystyle 0\leq y\leq \pi }
0
∘
≤
y
≤
180
∘
{\displaystyle 0^{\circ }\leq y\leq 180^{\circ }}
arctangent
y
=
arctan
(
x
)
{\displaystyle y=\arctan(x)}
x = tan (y )সব বাস্তব সংখ্যা
−
π
2
<
y
<
π
2
{\displaystyle -{\frac {\pi }{2}}<y<{\frac {\pi }{2}}}
−
90
∘
<
y
<
90
∘
{\displaystyle -90^{\circ }<y<90^{\circ }}
arccotangent
y
=
arccot
(
x
)
{\displaystyle y=\operatorname {arccot}(x)}
x = cot (y )সব বাস্তব সংখ্যা
0
<
y
<
π
{\displaystyle 0<y<\pi }
0
∘
<
y
<
180
∘
{\displaystyle 0^{\circ }<y<180^{\circ }}
arcsecant
y
=
arcsec
(
x
)
{\displaystyle y=\operatorname {arcsec}(x)}
x = sec (y )
|
x
|
≥
1
{\displaystyle {\left\vert x\right\vert }\geq 1}
0
≤
y
<
π
2
or
π
2
<
y
≤
π
{\displaystyle 0\leq y<{\frac {\pi }{2}}{\text{ or }}{\frac {\pi }{2}}<y\leq \pi }
0
∘
≤
y
<
90
∘
or
90
∘
<
y
≤
180
∘
{\displaystyle 0^{\circ }\leq y<90^{\circ }{\text{ or }}90^{\circ }<y\leq 180^{\circ }}
arccosecant
y
=
arccsc
(
x
)
{\displaystyle y=\operatorname {arccsc}(x)}
x = csc (y )
|
x
|
≥
1
{\displaystyle {\left\vert x\right\vert }\geq 1}
−
π
2
≤
y
<
0
or
0
<
y
≤
π
2
{\displaystyle -{\frac {\pi }{2}}\leq y<0{\text{ or }}0<y\leq {\frac {\pi }{2}}}
−
90
∘
≤
y
<
0
∘
or
0
∘
<
y
≤
90
∘
{\displaystyle -90^{\circ }\leq y<0^{\circ }{\text{ or }}0^{\circ }<y\leq 90^{\circ }}
arcsin(x ) (লাল) ও arccos(x ) (নীল) arctan(x ) ও arccot(x ) arcsec(x ) ও arccsc(x ) পূরক কোণ:
arccos
(
x
)
=
π
2
−
arcsin
(
x
)
arccot
(
x
)
=
π
2
−
arctan
(
x
)
arccsc
(
x
)
=
π
2
−
arcsec
(
x
)
{\displaystyle {\begin{aligned}\arccos(x)&={\frac {\pi }{2}}-\arcsin(x)\\[0.5em]\operatorname {arccot}(x)&={\frac {\pi }{2}}-\arctan(x)\\[0.5em]\operatorname {arccsc}(x)&={\frac {\pi }{2}}-\operatorname {arcsec}(x)\end{aligned}}}
ঋণাত্মক আরগুমেন্ট:
arcsin
(
−
x
)
=
−
arcsin
(
x
)
arccsc
(
−
x
)
=
−
arccsc
(
x
)
arccos
(
−
x
)
=
π
−
arccos
(
x
)
arcsec
(
−
x
)
=
π
−
arcsec
(
x
)
arctan
(
−
x
)
=
−
arctan
(
x
)
arccot
(
−
x
)
=
π
−
arccot
(
x
)
{\displaystyle {\begin{aligned}\arcsin(-x)&=-\arcsin(x)\\\operatorname {arccsc}(-x)&=-\operatorname {arccsc}(x)\\\arccos(-x)&=\pi -\arccos(x)\\\operatorname {arcsec}(-x)&=\pi -\operatorname {arcsec}(x)\\\arctan(-x)&=-\arctan(x)\\\operatorname {arccot}(-x)&=\pi -\operatorname {arccot}(x)\end{aligned}}}
অন্যোন্যক আরগুমেন্ট:
arcsin
(
1
x
)
=
arccsc
(
x
)
arccsc
(
1
x
)
=
arcsin
(
x
)
arccos
(
1
x
)
=
arcsec
(
x
)
arcsec
(
1
x
)
=
arccos
(
x
)
arctan
(
1
x
)
=
arccot
(
x
)
=
π
2
−
arctan
(
x
)
,
if
x
>
0
arctan
(
1
x
)
=
arccot
(
x
)
−
π
=
−
π
2
−
arctan
(
x
)
,
if
x
<
0
arccot
(
1
x
)
=
arctan
(
x
)
=
π
2
−
arccot
(
x
)
,
if
x
>
0
arccot
(
1
x
)
=
arctan
(
x
)
+
π
=
3
π
2
−
arccot
(
x
)
,
if
x
<
0
{\displaystyle {\begin{aligned}\arcsin \left({\frac {1}{x}}\right)&=\operatorname {arccsc}(x)&\\[0.3em]\operatorname {arccsc} \left({\frac {1}{x}}\right)&=\arcsin(x)&\\[0.3em]\arccos \left({\frac {1}{x}}\right)&=\operatorname {arcsec}(x)&\\[0.3em]\operatorname {arcsec} \left({\frac {1}{x}}\right)&=\arccos(x)&\\[0.3em]\arctan \left({\frac {1}{x}}\right)&=\operatorname {arccot}(x)&={\frac {\pi }{2}}-\arctan(x)\,,{\text{ if }}x>0\\[0.3em]\arctan \left({\frac {1}{x}}\right)&=\operatorname {arccot}(x)-\pi &=-{\frac {\pi }{2}}-\arctan(x)\,,{\text{ if }}x<0\\[0.3em]\operatorname {arccot} \left({\frac {1}{x}}\right)&=\arctan(x)&={\frac {\pi }{2}}-\operatorname {arccot}(x)\,,{\text{ if }}x>0\\[0.3em]\operatorname {arccot} \left({\frac {1}{x}}\right)&=\arctan(x)+\pi &={\frac {3\pi }{2}}-\operatorname {arccot}(x)\,,{\text{ if }}x<0\end{aligned}}}
উপরের অভেদগুলি
sin
{\displaystyle \sin }
csc
{\displaystyle \csc }
csc
=
1
sin
{\displaystyle \csc ={\tfrac {1}{\sin }}}
cos
{\displaystyle \cos }
sec
,
{\displaystyle \sec ,}
tan
{\displaystyle \tan }
cot
{\displaystyle \cot }
শুধু সাইন ব্যবহার করে:
arcsin
(
x
)
=
1
2
arccos
(
1
−
2
x
2
)
,
if
0
≤
x
≤
1
arcsin
(
x
)
=
arctan
(
x
1
−
x
2
)
arccos
(
x
)
=
1
2
arccos
(
2
x
2
−
1
)
,
if
0
≤
x
≤
1
arccos
(
x
)
=
arctan
(
1
−
x
2
x
)
arccos
(
x
)
=
arcsin
(
1
−
x
2
)
,
if
0
≤
x
≤
1
, from which you get
arccos
(
1
−
x
2
1
+
x
2
)
=
arcsin
(
2
x
1
+
x
2
)
,
if
0
≤
x
≤
1
arcsin
(
1
−
x
2
)
=
π
2
−
sgn
(
x
)
arcsin
(
x
)
arctan
(
x
)
=
arcsin
(
x
1
+
x
2
)
arccot
(
x
)
=
arccos
(
x
1
+
x
2
)
{\displaystyle {\begin{aligned}\arcsin(x)&={\frac {1}{2}}\arccos \left(1-2x^{2}\right)\,,{\text{ if }}0\leq x\leq 1\\\arcsin(x)&=\arctan \left({\frac {x}{\sqrt {1-x^{2}}}}\right)\\\arccos(x)&={\frac {1}{2}}\arccos \left(2x^{2}-1\right)\,,{\text{ if }}0\leq x\leq 1\\\arccos(x)&=\arctan \left({\frac {\sqrt {1-x^{2}}}{x}}\right)\\\arccos(x)&=\arcsin \left({\sqrt {1-x^{2}}}\right)\,,{\text{ if }}0\leq x\leq 1{\text{ , from which you get }}\\\arccos &\left({\frac {1-x^{2}}{1+x^{2}}}\right)=\arcsin \left({\frac {2x}{1+x^{2}}}\right)\,,{\text{ if }}0\leq x\leq 1\\\arcsin &\left({\sqrt {1-x^{2}}}\right)={\frac {\pi }{2}}-\operatorname {sgn}(x)\arcsin(x)\\\arctan(x)&=\arcsin \left({\frac {x}{\sqrt {1+x^{2}}}}\right)\\\operatorname {arccot}(x)&=\arccos \left({\frac {x}{\sqrt {1+x^{2}}}}\right)\end{aligned}}}
arctan
(
x
)
=
arccos
(
1
1
+
x
2
)
,
if
x
≥
0
{\displaystyle \arctan(x)=\arccos \left({\sqrt {\frac {1}{1+x^{2}}}}\right)\,,{\text{ if }}x\geq 0}
cos
(
arctan
(
x
)
)
=
1
1
+
x
2
=
cos
(
arccos
(
1
1
+
x
2
)
)
{\displaystyle \cos \left(\arctan \left(x\right)\right)={\sqrt {\frac {1}{1+x^{2}}}}=\cos \left(\arccos \left({\sqrt {\frac {1}{1+x^{2}}}}\right)\right)}
অর্ধ-কোণ সূত্র যেকে,
tan
(
θ
2
)
=
sin
(
θ
)
1
+
cos
(
θ
)
{\displaystyle \tan \left({\tfrac {\theta }{2}}\right)={\tfrac {\sin(\theta )}{1+\cos(\theta )}}}
arcsin
(
x
)
=
2
arctan
(
x
1
+
1
−
x
2
)
arccos
(
x
)
=
2
arctan
(
1
−
x
2
1
+
x
)
,
if
−
1
<
x
≤
1
arctan
(
x
)
=
2
arctan
(
x
1
+
1
+
x
2
)
{\displaystyle {\begin{aligned}\arcsin(x)&=2\arctan \left({\frac {x}{1+{\sqrt {1-x^{2}}}}}\right)\\[0.5em]\arccos(x)&=2\arctan \left({\frac {\sqrt {1-x^{2}}}{1+x}}\right)\,,{\text{ if }}-1<x\leq 1\\[0.5em]\arctan(x)&=2\arctan \left({\frac {x}{1+{\sqrt {1+x^{2}}}}}\right)\end{aligned}}}
z এর সাপেক্ষে অন্তরকলন:
d
d
z
arcsin
(
z
)
=
1
1
−
z
2
;
z
≠
−
1
,
+
1
d
d
z
arccos
(
z
)
=
−
1
1
−
z
2
;
z
≠
−
1
,
+
1
d
d
z
arctan
(
z
)
=
1
1
+
z
2
;
z
≠
−
i
,
+
i
d
d
z
arccot
(
z
)
=
−
1
1
+
z
2
;
z
≠
−
i
,
+
i
d
d
z
arcsec
(
z
)
=
1
z
2
1
−
1
z
2
;
z
≠
−
1
,
0
,
+
1
d
d
z
arccsc
(
z
)
=
−
1
z
2
1
−
1
z
2
;
z
≠
−
1
,
0
,
+
1
{\displaystyle {\begin{aligned}{\frac {d}{dz}}\arcsin(z)&{}={\frac {1}{\sqrt {1-z^{2}}}}\;;&z&{}\neq -1,+1\\{\frac {d}{dz}}\arccos(z)&{}=-{\frac {1}{\sqrt {1-z^{2}}}}\;;&z&{}\neq -1,+1\\{\frac {d}{dz}}\arctan(z)&{}={\frac {1}{1+z^{2}}}\;;&z&{}\neq -i,+i\\{\frac {d}{dz}}\operatorname {arccot}(z)&{}=-{\frac {1}{1+z^{2}}}\;;&z&{}\neq -i,+i\\{\frac {d}{dz}}\operatorname {arcsec}(z)&{}={\frac {1}{z^{2}{\sqrt {1-{\frac {1}{z^{2}}}}}}}\;;&z&{}\neq -1,0,+1\\{\frac {d}{dz}}\operatorname {arccsc}(z)&{}=-{\frac {1}{z^{2}{\sqrt {1-{\frac {1}{z^{2}}}}}}}\;;&z&{}\neq -1,0,+1\end{aligned}}}
শুধু মাত্র বাস্তব x এর জন্য:
d
d
x
arcsec
(
x
)
=
1
|
x
|
x
2
−
1
;
|
x
|
>
1
d
d
x
arccsc
(
x
)
=
−
1
|
x
|
x
2
−
1
;
|
x
|
>
1
{\displaystyle {\begin{aligned}{\frac {d}{dx}}\operatorname {arcsec}(x)&{}={\frac {1}{|x|{\sqrt {x^{2}-1}}}}\;;&|x|>1\\{\frac {d}{dx}}\operatorname {arccsc}(x)&{}=-{\frac {1}{|x|{\sqrt {x^{2}-1}}}}\;;&|x|>1\end{aligned}}}
এগুলি ত্রিকোণমিতিক অপেক্ষকের সাহায্যেও নির্ণয় করা সম্ভব। যেমন, যদি
x
=
sin
θ
{\displaystyle x=\sin \theta }
d
x
/
d
θ
=
cos
θ
=
1
−
x
2
,
{\textstyle dx/d\theta =\cos \theta ={\sqrt {1-x^{2}}},}
d
d
x
arcsin
(
x
)
=
d
θ
d
x
=
1
d
x
/
d
θ
=
1
1
−
x
2
.
{\displaystyle {\frac {d}{dx}}\arcsin(x)={\frac {d\theta }{dx}}={\frac {1}{dx/d\theta }}={\frac {1}{\sqrt {1-x^{2}}}}.}
নির্দিষ্ট সমাকল [ সম্পাদনা ]
arcsin
(
x
)
=
∫
0
x
1
1
−
z
2
d
z
,
|
x
|
≤
1
arccos
(
x
)
=
∫
x
1
1
1
−
z
2
d
z
,
|
x
|
≤
1
arctan
(
x
)
=
∫
0
x
1
z
2
+
1
d
z
,
arccot
(
x
)
=
∫
x
∞
1
z
2
+
1
d
z
,
arcsec
(
x
)
=
∫
1
x
1
z
z
2
−
1
d
z
=
π
+
∫
−
x
−
1
1
z
z
2
−
1
d
z
,
x
≥
1
arccsc
(
x
)
=
∫
x
∞
1
z
z
2
−
1
d
z
=
∫
−
∞
−
x
1
z
z
2
−
1
d
z
,
x
≥
1
{\displaystyle {\begin{aligned}\arcsin(x)&{}=\int _{0}^{x}{\frac {1}{\sqrt {1-z^{2}}}}\,dz\;,&|x|&{}\leq 1\\\arccos(x)&{}=\int _{x}^{1}{\frac {1}{\sqrt {1-z^{2}}}}\,dz\;,&|x|&{}\leq 1\\\arctan(x)&{}=\int _{0}^{x}{\frac {1}{z^{2}+1}}\,dz\;,\\\operatorname {arccot}(x)&{}=\int _{x}^{\infty }{\frac {1}{z^{2}+1}}\,dz\;,\\\operatorname {arcsec}(x)&{}=\int _{1}^{x}{\frac {1}{z{\sqrt {z^{2}-1}}}}\,dz=\pi +\int _{-x}^{-1}{\frac {1}{z{\sqrt {z^{2}-1}}}}\,dz\;,&x&{}\geq 1\\\operatorname {arccsc}(x)&{}=\int _{x}^{\infty }{\frac {1}{z{\sqrt {z^{2}-1}}}}\,dz=\int _{-\infty }^{-x}{\frac {1}{z{\sqrt {z^{2}-1}}}}\,dz\;,&x&{}\geq 1\\\end{aligned}}}
যেখানে x = ১।
arcsin
(
z
)
=
z
+
(
1
2
)
z
3
3
+
(
1
⋅
3
2
⋅
4
)
z
5
5
+
(
1
⋅
3
⋅
5
2
⋅
4
⋅
6
)
z
7
7
+
⋯
=
∑
n
=
0
∞
(
2
n
−
1
)
!
!
(
2
n
)
!
!
z
2
n
+
1
2
n
+
1
=
∑
n
=
0
∞
(
2
n
)
!
(
2
n
n
!
)
2
z
2
n
+
1
2
n
+
1
;
|
z
|
≤
1
{\displaystyle {\begin{aligned}\arcsin(z)&=z+\left({\frac {1}{2}}\right){\frac {z^{3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{5}}{5}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {z^{7}}{7}}+\cdots \\[5pt]&=\sum _{n=0}^{\infty }{\frac {(2n-1)!!}{(2n)!!}}{\frac {z^{2n+1}}{2n+1}}\\[5pt]&=\sum _{n=0}^{\infty }{\frac {(2n)!}{(2^{n}n!)^{2}}}{\frac {z^{2n+1}}{2n+1}}\,;\qquad |z|\leq 1\end{aligned}}}
arctan
(
z
)
=
z
−
z
3
3
+
z
5
5
−
z
7
7
+
⋯
=
∑
n
=
0
∞
(
−
1
)
n
z
2
n
+
1
2
n
+
1
;
|
z
|
≤
1
z
≠
i
,
−
i
{\displaystyle \arctan(z)=z-{\frac {z^{3}}{3}}+{\frac {z^{5}}{5}}-{\frac {z^{7}}{7}}+\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}z^{2n+1}}{2n+1}}\,;\qquad |z|\leq 1\qquad z\neq i,-i}
অন্যান্য ত্রিকোণমিতিক অপেক্ষকের সাপেক্ষে সিরিজ নির্ধারিত করা সম্ভব। যেমন,
arccos
(
x
)
=
π
/
2
−
arcsin
(
x
)
{\displaystyle \arccos(x)=\pi /2-\arcsin(x)}
arccsc
(
x
)
=
arcsin
(
1
/
x
)
{\displaystyle \operatorname {arccsc}(x)=\arcsin(1/x)}
[৪]
2
(
arcsin
(
x
2
)
)
2
=
∑
n
=
1
∞
x
2
n
n
2
(
2
n
n
)
.
{\displaystyle 2\left(\arcsin \left({\frac {x}{2}}\right)\right)^{2}=\sum _{n=1}^{\infty }{\frac {x^{2n}}{n^{2}{\binom {2n}{n}}}}.}
লেওনার্ড অয়লার কর্তৃক আবিষ্কৃত সূত্র (টেলর ধারা অপেক্ষা দ্রুততর নির্ণয়যোগ্য):
arctan
(
z
)
=
z
1
+
z
2
∑
n
=
0
∞
∏
k
=
1
n
2
k
z
2
(
2
k
+
1
)
(
1
+
z
2
)
.
{\displaystyle \arctan(z)={\frac {z}{1+z^{2}}}\sum _{n=0}^{\infty }\prod _{k=1}^{n}{\frac {2kz^{2}}{(2k+1)(1+z^{2})}}.}
[৫] এছাড়াও, এটিকে নিম্নলিখিত ভাবেও প্রকাশ করা সম্ভব:
arctan
(
z
)
=
∑
n
=
0
∞
2
2
n
(
n
!
)
2
(
2
n
+
1
)
!
z
2
n
+
1
(
1
+
z
2
)
n
+
1
.
{\displaystyle \arctan(z)=\sum _{n=0}^{\infty }{\frac {2^{2n}(n!)^{2}}{(2n+1)!}}{\frac {z^{2n+1}}{(1+z^{2})^{n+1}}}.}
আর্কট্যানজেন্টের আরেকটি সিরিজ হল:
arctan
(
z
)
=
i
∑
n
=
1
∞
1
2
n
−
1
(
1
(
1
+
2
i
/
z
)
2
n
−
1
−
1
(
1
−
2
i
/
z
)
2
n
−
1
)
,
{\displaystyle \arctan(z)=i\sum _{n=1}^{\infty }{\frac {1}{2n-1}}\left({\frac {1}{(1+2i/z)^{2n-1}}}-{\frac {1}{(1-2i/z)^{2n-1}}}\right),}
যেগানে
i
=
−
1
{\displaystyle i={\sqrt {-1}}}
[৬]
আর্কট্যানজেন্টের অসীম ভগ্নাংশ [ সম্পাদনা ]
arctan
(
z
)
=
z
1
+
(
1
z
)
2
3
−
1
z
2
+
(
3
z
)
2
5
−
3
z
2
+
(
5
z
)
2
7
−
5
z
2
+
(
7
z
)
2
9
−
7
z
2
+
⋱
=
z
1
+
(
1
z
)
2
3
+
(
2
z
)
2
5
+
(
3
z
)
2
7
+
(
4
z
)
2
9
+
⋱
{\displaystyle \arctan(z)={\frac {z}{1+{\cfrac {(1z)^{2}}{3-1z^{2}+{\cfrac {(3z)^{2}}{5-3z^{2}+{\cfrac {(5z)^{2}}{7-5z^{2}+{\cfrac {(7z)^{2}}{9-7z^{2}+\ddots }}}}}}}}}}={\frac {z}{1+{\cfrac {(1z)^{2}}{3+{\cfrac {(2z)^{2}}{5+{\cfrac {(3z)^{2}}{7+{\cfrac {(4z)^{2}}{9+\ddots }}}}}}}}}}}
অনির্দিষ্ট সমাকল [ সম্পাদনা ] z এর বাস্তব ও জটিল মানের জন্য:
∫
arcsin
(
z
)
d
z
=
z
arcsin
(
z
)
+
1
−
z
2
+
C
∫
arccos
(
z
)
d
z
=
z
arccos
(
z
)
−
1
−
z
2
+
C
∫
arctan
(
z
)
d
z
=
z
arctan
(
z
)
−
1
2
ln
(
1
+
z
2
)
+
C
∫
arccot
(
z
)
d
z
=
z
arccot
(
z
)
+
1
2
ln
(
1
+
z
2
)
+
C
∫
arcsec
(
z
)
d
z
=
z
arcsec
(
z
)
−
ln
[
z
(
1
+
z
2
−
1
z
2
)
]
+
C
∫
arccsc
(
z
)
d
z
=
z
arccsc
(
z
)
+
ln
[
z
(
1
+
z
2
−
1
z
2
)
]
+
C
{\displaystyle {\begin{aligned}\int \arcsin(z)\,dz&{}=z\,\arcsin(z)+{\sqrt {1-z^{2}}}+C\\\int \arccos(z)\,dz&{}=z\,\arccos(z)-{\sqrt {1-z^{2}}}+C\\\int \arctan(z)\,dz&{}=z\,\arctan(z)-{\frac {1}{2}}\ln \left(1+z^{2}\right)+C\\\int \operatorname {arccot}(z)\,dz&{}=z\,\operatorname {arccot}(z)+{\frac {1}{2}}\ln \left(1+z^{2}\right)+C\\\int \operatorname {arcsec}(z)\,dz&{}=z\,\operatorname {arcsec}(z)-\ln \left[z\left(1+{\sqrt {\frac {z^{2}-1}{z^{2}}}}\right)\right]+C\\\int \operatorname {arccsc}(z)\,dz&{}=z\,\operatorname {arccsc}(z)+\ln \left[z\left(1+{\sqrt {\frac {z^{2}-1}{z^{2}}}}\right)\right]+C\end{aligned}}}
x (বাস্তব) ≥ 1:
∫
arcsec
(
x
)
d
x
=
x
arcsec
(
x
)
−
ln
(
x
+
x
2
−
1
)
+
C
∫
arccsc
(
x
)
d
x
=
x
arccsc
(
x
)
+
ln
(
x
+
x
2
−
1
)
+
C
{\displaystyle {\begin{aligned}\int \operatorname {arcsec}(x)\,dx&{}=x\,\operatorname {arcsec}(x)-\ln \left(x+{\sqrt {x^{2}-1}}\right)+C\\\int \operatorname {arccsc}(x)\,dx&{}=x\,\operatorname {arccsc}(x)+\ln \left(x+{\sqrt {x^{2}-1}}\right)+C\end{aligned}}}
x (বাস্তব), যখন -১ থেকে +১ এর মধ্যে নয়:
∫
arcsec
(
x
)
d
x
=
x
arcsec
(
x
)
−
sgn
(
x
)
ln
|
x
+
x
2
−
1
|
+
C
∫
arccsc
(
x
)
d
x
=
x
arccsc
(
x
)
+
sgn
(
x
)
ln
|
x
+
x
2
−
1
|
+
C
{\displaystyle {\begin{aligned}\int \operatorname {arcsec}(x)\,dx&{}=x\,\operatorname {arcsec}(x)-\operatorname {sgn}(x)\ln \left|x+{\sqrt {x^{2}-1}}\right|+C\\\int \operatorname {arccsc}(x)\,dx&{}=x\,\operatorname {arccsc}(x)+\operatorname {sgn}(x)\ln \left|x+{\sqrt {x^{2}-1}}\right|+C\end{aligned}}}
∫
u
d
v
=
u
v
−
∫
v
d
u
{\displaystyle \int u\,dv=uv-\int v\,du}
ইন্টিগ্রেশন বাই পার্টস ),
u
=
arcsin
(
x
)
d
v
=
d
x
d
u
=
d
x
1
−
x
2
v
=
x
{\displaystyle {\begin{aligned}u&=\arcsin(x)&dv&=dx\\du&={\frac {dx}{\sqrt {1-x^{2}}}}&v&=x\end{aligned}}}
তাহলে
∫
arcsin
(
x
)
d
x
=
x
arcsin
(
x
)
−
∫
x
1
−
x
2
d
x
,
{\displaystyle \int \arcsin(x)\,dx=x\arcsin(x)-\int {\frac {x}{\sqrt {1-x^{2}}}}\,dx,}
প্রতিস্থাপন করে
w
=
1
−
x
2
,
d
w
=
−
2
x
d
x
{\displaystyle w=1-x^{2},\ dw=-2x\,dx}
∫
arcsin
(
x
)
d
x
=
x
arcsin
(
x
)
+
1
−
x
2
+
C
{\displaystyle \int \arcsin(x)\,dx=x\arcsin(x)+{\sqrt {1-x^{2}}}+C}
↑ Weisstein, Eric W.। "Inverse Trigonometric Functions" । mathworld.wolfram.com (ইংরেজি ভাষায়)। সংগ্রহের তারিখ ২০২০-০৮-২৯ । ↑ Cook, John D. (২০২১-০২-১১)। "Trig functions across programming languages" । johndcook.com (blog)। সংগ্রহের তারিখ ২০২১-০৩-১০ । ↑ "Inverse trigonometric functions" । Brilliant Math & Science (brilliant.org) (ইংরেজি ভাষায়)। সংগ্রহের তারিখ ২০২০-০৮-২৯ । ↑ উদ্ধৃতি ত্রুটি: <ref> ট্যাগ বৈধ নয়; Borwein_2004 নামের সূত্রটির জন্য কোন লেখা প্রদান করা হয়নি ↑ Hwang Chien-Lih (২০০৫), "An elementary derivation of Euler's series for the arctangent function", The Mathematical Gazette , 89 (516): 469–470, এসটুসিআইডি 123395287 , ডিওআই :10.1017/S0025557200178404 ↑ S. M. Abrarov and B. M. Quine (২০১৮), "A formula for pi involving nested radicals", The Ramanujan Journal , 46 (3): 657–665, arXiv :1610.07713 এসটুসিআইডি 119150623 , ডিওআই :10.1007/s11139-018-9996-8




 , এসটুসিআইডি 119150623, ডিওআই:10.1007/s11139-018-9996-8
, এসটুসিআইডি 119150623, ডিওআই:10.1007/s11139-018-9996-8






















![{\displaystyle {\begin{aligned}\arccos(x)&={\frac {\pi }{2}}-\arcsin(x)\\[0.5em]\operatorname {arccot}(x)&={\frac {\pi }{2}}-\arctan(x)\\[0.5em]\operatorname {arccsc}(x)&={\frac {\pi }{2}}-\operatorname {arcsec}(x)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec43798232f580abb074cf15f3d77692edd36af0)

![{\displaystyle {\begin{aligned}\arcsin \left({\frac {1}{x}}\right)&=\operatorname {arccsc}(x)&\\[0.3em]\operatorname {arccsc} \left({\frac {1}{x}}\right)&=\arcsin(x)&\\[0.3em]\arccos \left({\frac {1}{x}}\right)&=\operatorname {arcsec}(x)&\\[0.3em]\operatorname {arcsec} \left({\frac {1}{x}}\right)&=\arccos(x)&\\[0.3em]\arctan \left({\frac {1}{x}}\right)&=\operatorname {arccot}(x)&={\frac {\pi }{2}}-\arctan(x)\,,{\text{ if }}x>0\\[0.3em]\arctan \left({\frac {1}{x}}\right)&=\operatorname {arccot}(x)-\pi &=-{\frac {\pi }{2}}-\arctan(x)\,,{\text{ if }}x<0\\[0.3em]\operatorname {arccot} \left({\frac {1}{x}}\right)&=\arctan(x)&={\frac {\pi }{2}}-\operatorname {arccot}(x)\,,{\text{ if }}x>0\\[0.3em]\operatorname {arccot} \left({\frac {1}{x}}\right)&=\arctan(x)+\pi &={\frac {3\pi }{2}}-\operatorname {arccot}(x)\,,{\text{ if }}x<0\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2fca7d530f42c84ed92b5895ccbafb013dc6645)











![{\displaystyle {\begin{aligned}\arcsin(x)&=2\arctan \left({\frac {x}{1+{\sqrt {1-x^{2}}}}}\right)\\[0.5em]\arccos(x)&=2\arctan \left({\frac {\sqrt {1-x^{2}}}{1+x}}\right)\,,{\text{ if }}-1<x\leq 1\\[0.5em]\arctan(x)&=2\arctan \left({\frac {x}{1+{\sqrt {1+x^{2}}}}}\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7dd6a9370a877ca5e198e28b7582bd06b377bdc3)






![{\displaystyle {\begin{aligned}\arcsin(z)&=z+\left({\frac {1}{2}}\right){\frac {z^{3}}{3}}+\left({\frac {1\cdot 3}{2\cdot 4}}\right){\frac {z^{5}}{5}}+\left({\frac {1\cdot 3\cdot 5}{2\cdot 4\cdot 6}}\right){\frac {z^{7}}{7}}+\cdots \\[5pt]&=\sum _{n=0}^{\infty }{\frac {(2n-1)!!}{(2n)!!}}{\frac {z^{2n+1}}{2n+1}}\\[5pt]&=\sum _{n=0}^{\infty }{\frac {(2n)!}{(2^{n}n!)^{2}}}{\frac {z^{2n+1}}{2n+1}}\,;\qquad |z|\leq 1\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a0f778db7f760db059cf12f13ee5c2bf239fbb2f)









![{\displaystyle {\begin{aligned}\int \arcsin(z)\,dz&{}=z\,\arcsin(z)+{\sqrt {1-z^{2}}}+C\\\int \arccos(z)\,dz&{}=z\,\arccos(z)-{\sqrt {1-z^{2}}}+C\\\int \arctan(z)\,dz&{}=z\,\arctan(z)-{\frac {1}{2}}\ln \left(1+z^{2}\right)+C\\\int \operatorname {arccot}(z)\,dz&{}=z\,\operatorname {arccot}(z)+{\frac {1}{2}}\ln \left(1+z^{2}\right)+C\\\int \operatorname {arcsec}(z)\,dz&{}=z\,\operatorname {arcsec}(z)-\ln \left[z\left(1+{\sqrt {\frac {z^{2}-1}{z^{2}}}}\right)\right]+C\\\int \operatorname {arccsc}(z)\,dz&{}=z\,\operatorname {arccsc}(z)+\ln \left[z\left(1+{\sqrt {\frac {z^{2}-1}{z^{2}}}}\right)\right]+C\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e3e2dde92bb82231c4326e45ce8b50e7298688bb)






