কুলম্বের সূত্র

কুলম্বের সূত্র তথা কুলম্বের বিপরীত বর্গীয় সূত্র হলো পদার্থবিজ্ঞানের এমন একটি সূত্র, যা দুটি আধানের (চার্জের) মধ্যবর্তী আকর্ষণ বা বিকর্ষণের স্বরূপ ব্যাখ্যা করে। ১৭৮৫ খ্রিষ্টাব্দ ফরাসি পদার্থবিদ চার্লস-অগাস্টিন-দে-কুলম্ব সূত্রটি আবিষ্কার করেন এবং তিনি তড়িৎ চুম্বকত্বের যথেষ্ট উন্নতি সাধন করেন। এই সূত্র নিউটনের মহাকর্ষীয় সূত্র-এর সদৃশ। কুলম্বের সূত্র থেকে গাউসের সূত্র পাওয়া যায় এবং বিপরীতক্রমে গাউসের সূত্র থেকেও কুলম্বের সূত্র পাওয়া যায়। এই সূত্রটি ব্যাপকভাবে পরীক্ষিত এবং প্রমাণিত।

F∝q1q2 F∝1/r ²

F=kq1q2/r2

প্রথম সূত্র

একই ধরনের চার্জ পরস্পরকে বিকর্ষণ করে এবং বিপরীতধর্মী চার্জ পরস্পরকে আকর্ষণ করে‌।

দ্বিতীয় সূত্র

দুটি স্থির বিন্দু আধান এর মধ্যে কার্যকর আকর্ষণ বা বিকর্ষণ বল আধান দ্বয়ের পরিমাণ এর গুণফলের সমানুপাতিক এবং তাদের মধ্যবর্তী দূরত্বের বর্গের ব্যস্তানুপাতিক

অর্থাৎ F ∝ q1q2

    F ∝ 1/r² 
   বা   F = k• q1•q2/r²
   যেখানে k(কুলম্বের ধ্রুবক) = 1/4πε
     ε = 8.85×10–¹² C²/N•M² বা C.G.S. পদ্ধতিতে

ইতিহাস

প্রাচীন ভূ-মধ্যসাগরীয়রা ধারণা করতো যে,রডের আম্বর নিশ্চিত বস্তু,যেটাকে বিড়ালের লোমের সাথে ঘর্ষন করলে পালকের এর মত বস্তুকে আকর্ষণ করে।মিলিটাস শহরের বিজ্ঞানী থেলাস ৬০০ শতাব্দির দিকে স্থির তড়িৎ এর ধারা তৈরী করে পর্যবেক্ষণ করেন এবং তিনি বিশ্বাস করতেন যে ঘর্ষণ অনুষ্ঠিত আম্বর চুম্বকীয়,অন্যভাবে খনিজ পদার্থ চুম্বকীয় কিন্তু যার ঘর্ষণ এর দরকার নেই। থেলাস এর ধারণা ভুল ছিল,সে বিশ্বাস করত যে এই আকর্ষণের কারণ হল চুম্বকীয় প্রভাব। কিন্তু, পরবর্তীতে বিজ্ঞান চুম্বক এবং তড়িৎ এর মধ্যে একটি সম্পর্ক প্রমাণ করে। ১৬০০ শতাব্দী পর্যন্ত তড়িৎ ছিল সহস্র বছরের কল্পনা, তখন ইংরেজ বিজ্ঞানী উইলিয়াম গিলবা্র্ট তড়িৎ এবং চুম্বকের সতর্কভাবে একটি পরীক্ষা করেছিলেন।

শার্ল-অগুস্তিন দু কুলম্ব

এই পরীক্ষায় তিনি আম্বর এর ঘর্ষণ দ্বারা স্থির তড়িৎ থেকে প্রভাব পার্থক্য করেছিলেন। তিনি ‘ইলেক্ট্রিকাস’ নামক নতুন ল্যাটিন শব্দ আবিষ্কার করেন(আম্বরের অথবা আম্বরের মতো গ্রীক শব্দ আম্বর)।যার মানে ঘর্ষণের পর কোন বস্তুর আকর্ষণী ধর্মকে বূঝায়।এই সমিতি দুটি ইংরেজি শব্দ ইলেক্ট্রিক এবং ইলেক্ট্রিসিটি দেয়। যা ১৬৪৬ সালে থমাস ব্রাউন এর সেউডক্সিয়া এপিদেমিকার (Pseudopodia Epidemica) প্রথম মুদ্রণে প্রকাশ পায়।

কুলম্বের টরসন ভারসাম্য

১৮ শতকের শুরুর দিকে বিজ্ঞানীরা সন্দেহ .করেছিল মধ্যাকর্ষণ শক্তির প্রভাবে তড়িৎ বল দুরত্তের সাথে হ্রাস পায়। যা ড্যানিয়েল বেরনলি এবং আলেক্সান্দ্রো ভোল্টা অন্তর্ভুক্ত করেন। তারা তড়িৎ ধারক এর উভয়পাতের বল পরিমাপ করেন।১৭৫৮ সালে ফ্রেঞ্চ আইপিনাস বিপরীত বর্গীয় সুত্র বের করেন। তড়িৎ চার্জ এর বলয়ের পরীক্ষার উপর ভিত্তি করে ইংল্যান্ড এর বিজ্ঞানী জোসেফ প্রিস্টলি একটি প্রস্তাব করেন যে,তড়িৎ বল বিপরীত বর্গীয় সূত্র মেনে চলে এবং এটি নিউটন এর সার্বজনীন অভিকর্ষ সূত্রের অনুরুপ,তবে তিনি এ নিয়ে আর বেশি গবেষণা করেননি।পরবর্তীতে ১৭৬৭ সালে তিনি অনুমান করেছিলেন যে, বিপরীত বর্গীয় দুরত্বের কারণে এই বলের চার্জ তারতম্য ঘটে। ১৭৬৯ সালে স্কটিশ পদারথবিদ রবিনসন ঘোষণা করেন যে, তার হিসাব মতে দুটি সমান চিহ্ন এর বলয়ের বিকর্ষণ বলের তারতম্য x-2.06।১৭৭০ এর শুরুর দিকে ইংল্যান্ড এর বিজ্ঞানী হেনরি ক্যাভেন্ডিস চার্জ কাঠামোতে বলের নির্ভরশীলতার জন্য উভয় দূরত্ব এবং চার্জ আবিষ্কার করেছিল কিন্তু প্রকাশ করেন নি। সর্বশেষ, ১৭৮৫ সালে ফরাসি পদার্থবিদ চার্লস অগাস্টটিন দ্যা কুলম্ব তার তড়িৎ এবং চুম্বক সম্পর্কিত প্রথম তিনটি প্রতিবেদন প্রকাশ করেন যেখানে তিনি তার সুত্র প্রদান করেছিলেন।তড়িৎ চুম্বকত্ব তত্তের উন্নতির জন্য এই প্রকাশনা ছিল খুব গুরুত্বপূর্ণ। তিনি চার্জ এর কণার আকর্ষণ এবং বিকর্ষণ বল বের করার জন্য কুণ্ডলী সমতা ব্যবহার করেন।এছাড়া চার্জ কণা দুটির চার্জ এর দূরতের বাস্তানুপাতিক। এই কুণ্ডলীর কাঠামো একটি চিকন সুতা দারা বারের সাথে ঝুলানো থাকে।এই সুতা কুণ্ডলীর সাথে খুবই হালকাভাবে ক্রিয়া করে। কুলম্ব এর পরীক্ষাতে, কুণ্ডলীটি সিল্কের সুতার সাথে এক প্রান্তে একটি ধাতব বল এবং অপর প্রান্তে একটি হালকা রডের সাথে যুক্ত ছিল।এই প্রথম বলটি স্থির তড়িৎ এর চার্জএ চার্জিত ছিল এবং অপর বলটি সমান চার্জএ চার্জিত করে এর নিকট আনা হয়েছিল। চার্জিত বল দুটি একটি নির্দিষ্ট কোণের মাধ্যমে সূক্ষ্ সুতার দারা একে অপরকে প্রতিহত করে,যা যন্ত্রটির উপরের স্কেল থেকে বুঝা যায়।এটা জানতে হলে,মাধমের কোণ তৈরিতে কতটুকু বল লাগবে তা জানতে হবে।কুলম্ব গোলক দুটির মধ্যে বল এবং সমানুপাতিক এবং বাস্তানুপাতিক বের করতে সক্ষম হয়েছিলেন।

সূত্র

দুটি স্থির বিন্দু আধানের মধ্যে ক্রিয়াশীল আকর্ষণ বা বিকর্ষণ বল তাদের আধানের পরিমাণের গুণফলের সমানুপাতিক এবং তাদের মধ্যের দূরত্বের বর্গের ব্যাস্তানুপাতিক এবং এই বল আধানদ্বয়ের সংযোজী রেখা বরাবর ক্রিয়া করে এবং মাধ্যমের প্রকৃতির ওপর নির্ভর করে। এই বল একইভাবে সোজাসুজি অংশগ্রহণ করে।যদি চার্জ এর চিহ্ন একই হয় তবে স্থির তড়িৎ বল একে অপরকে বিকর্ষণ করবে।আর যদি চার্জ এর চিহ্ন ভিন্ন হয়,তবে এইবল একে অপরকে আকর্ষণ করবে।

A graphical representation of Coulomb's law

কুলম্ব এর সুত্রকে অন্য উপায় গাণিতিকভাবে সহজে ব্যাখ্যা করা যায়।স্কেলার এবং ভেক্টর আকারে গাণিতিক সমীকরণ হল

$|\mathbf {F} |=k_{e}{|q_{1}q_{2}| \over r^{2}}\qquad$ and $\qquad \mathbf {F} _{1}=k_{e}{\frac {q_{1}q_{2}}{{|\mathbf {r} _{12}|}^{2}}}\mathbf {\hat {r}} _{12},\qquad$

যেখানে $k_{e}$ হল কুলম্ব এর ধ্রুবক। যার মান ($k_{e}=8.987\,551\,787\,368\,176\,4\times 10^{9}\ \mathrm {N\cdot m^{2}\cdot C} ^{-2}$), $q_{1}$ এবং $q_{2}$ হল চার্জ এর মান,এখানে $r$ হল স্কেলার রাশি দুটির মধ্যবর্তী দূরত্ব,ভেক্টর ${\boldsymbol {r_{12}}}={\boldsymbol {r_{1}-r_{2}}}$ হল চার্জ দুটির ভেক্টরীয় দূরত্ব এবং ${\boldsymbol {{\hat {r}}_{12}}}={{\boldsymbol {r_{12}}}/|{\boldsymbol {r_{12}}}|}$। (এর মান একটি একক ভেক্টর $q_{2}$ হতে $q_{1}$)।ভেক্টর সমীকরণ হিসাব মতে বল $\mathbf {F} _{1}$,$q_{1}$ দারা $q_{2}$ এর উপর প্রয়োগ করে।যদি এর পরিবর্তে $\mathbf {r} _{21}$ ব্যবহার হয়,তখন $q_{2}$ এর উপরের প্রভাবও পাওয়া যাবে।এটাও নিউটনের ৩য় সুত্র $\mathbf {F} _{2}=-\mathbf {F} _{1}$ থেকে হিসাব করা যায়।

একক

তড়িৎ চুম্বকীয় তত্ত্বে এস আই কে মানসম্মত একক ব্যবহার করা হয়।বলের একক নিউটন,চার্জ কুলম্ব এবং দূরত্ব মিটার। কুলম্ব এর ধ্রুবক $k_{e}=1/(4\pi \varepsilon _{0}\varepsilon )$।$\varepsilon _{0}$ ধ্রুবক একক C² m⁻² N⁻¹।এখানে $\varepsilon$ আপেক্ষিক উপাদান যেখানে চার্জ পরিপূর্ণ এবং মাত্রাহীন।তড়িৎ ক্ষেত্রের SI একক ভোল্ট/মিটার,নিউটন/কুলম্ব অথবা টেসলা মিটার/সেকেন্ড।

কুলম্ব এর সুত্র এবং কুলম্ব এর ধ্রুবককে অন্যভাবেও ব্যাখ্যা করা যায়

পারমাণবিক একক- পারমাণবিক এককে বলের একক হার্টরেস/বোরের ব্যাসার্ধ। চার্জ এর পরিবর্তে মৌলিক চার্জ এবং দূরতের পরিবর্তে বোরের ব্যাসার্ধ।

তড়িৎ একক বা গাউসের একক-তড়িৎ একক বা গাউসের একক এর মধ্যে একক চার্জ এর ব্যাখ্যা করা হয় যে কুলম্ব এর ধ্রুবক k অদৃশ্য কারণ এর একটা মান আছে এবং মাত্রাহীন।

তড়িৎক্ষেত্র

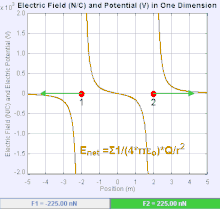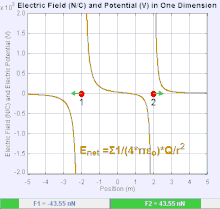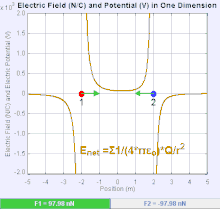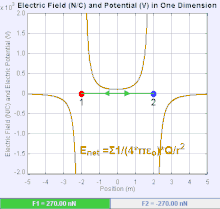
তড়িৎ ক্ষেত্র হল একটি ভেক্টর ক্ষেত্র যেখানে প্রত্যেকটি বিন্দুর কুলম্ব এর বল দ্বারা পরীক্ষা করা হয়। একে স্কেলার ও ভেক্টর দুইভাবেই প্রকাশ করা যায়। ভেক্টর রাশিটি হল তড়িৎপ্রাবল্য(E= F/q) অর্থাৎ একক আধানকে তড়িৎক্ষেত্রে আনতে যে বল প্রয়োজন, তাকে তড়িৎপ্রাবল্য বলে। আবার স্থির তাড়িতিক কার্য, W=(1/4πε)q¹q²/r = r•F তাই একক আধানকে তড়িৎক্ষেত্রের কোনো বিন্দুতে আনতে যে কার্য করতে হয়, তাকে তড়িৎবিভব বলে। V = W/q²= (1/4πε)•q/r এটি তড়িৎক্ষেত্র মাপার স্কেলার মাপক।

এটা খুব সাধারণ ব্যাপার,তড়িৎ ক্ষেত্রের সৃষ্টি হয়েছে শুধুমাত্র একটি বিন্দু চার্জ এর উৎস থেকে। ${\boldsymbol {F}}=q_{t}{\boldsymbol {E}}$ কুলম্ব এর বলের উপর চার্জ $q_{t}$ এবং তড়িৎ ক্ষেত্র ${\boldsymbol {E}}$ এর উপর নির্ভর করে।যদি তড়িৎ ক্ষেত্র ধনাত্মক চার্জ $q_{t}$ হতে সৃষ্টি হয়,তবে তড়িৎ ক্ষেত্রের দিক বাহ্যিকভাবে বাহিরের দিকে হয়,আর ঋণাত্মক উৎসের চার্জ এর ক্ষেত্রে দিক ভেতরের দিকে হয়।তড়িৎ ক্ষেত্রের মান কুলম্ব এর সূত্র হতে পাওয়া যায়।একটি বিন্দুকে চার্জ এর উৎস ধরতে হবে এবং অন্যটি হবে পরীক্ষামুলক চার্জ।কুলম্ব এর সূত্র হতে পাওয়া যায় যে,তড়িৎ ক্ষেত্র ${\boldsymbol {E}}$ তৈরি হয় একটি মাত্র বিন্দু চার্জ থেকে এবং একটি নির্দিষ্ট দূরত্ব $r$ থেকে।যার ফলে :$|{\boldsymbol {E}}|={1 \over 4\pi \varepsilon _{0}}{|q| \over r^{2}}$.যদি তড়িৎ চার্জ দুটির চিহ্ন একই হয় তবে একে অপরকে বিকর্ষণ করবে,যদি চিহ্ন বিপরীত হয় তবে একে অপরকে আকর্ষণ করবে।

If the two charges have the same sign, the electrostatic force between them is repulsive; if they have different sign, the force between them is attractive.

কুলম্বের ধ্রুবক

কুলম্বের ধ্রুবক একটি সমানুপাতিক উপাদান যা কুলম্বের সূত্রের সাথে স্থির তড়িৎ এর সম্পর্ক তুলে ধরে।

কুলম্বের সূত্রের সঠিক মান হল: ${\begin{aligned}k_{e}&={\frac {1}{4\pi \varepsilon _{0}}}={\frac {c_{0}^{2}\mu _{0}}{4\pi }}=c_{0}^{2}\times 10^{-7}\ \mathrm {H\cdot m} ^{-1}\\&=8.987\,551\,787\,368\,176\,4\times 10^{9}\ \mathrm {N\cdot m^{2}\cdot C} ^{-2}\end{aligned}}$

কুলম্বের সূত্রের শর্ত

1. চার্জটি অবশ্যই বিন্দু চার্জ হিসাবে গণনা করা হবে।
2. তারা একে অপরকে সমীহ করবে।

স্কেলার কাঠামো

যখন শুধুমাত্র স্থির তড়িৎ বলের মান বের করতে বলা হয়[দিক নয়]তখন স্কেলার রুপ ব্যবহার করা সবচেয়ে সহজ। কুলম্বের সুত্রের স্কেলার কাঠামো অনুযায়ী স্থির তড়িৎ বল ${\boldsymbol {F}}$ এবং $q_{1}$,$q_{2}$ চার্জ বিন্দু দুটির মান এবং চিহ্ন একই সাথে অনুসরণ করে :$|{\boldsymbol {F}}|=k_{e}{|q_{1}q_{2}| \over r^{2}}$ যেখানে $k_{e}$ হল কুলম্ব এর ধ্রুবক এবং এখানে $r$ হল স্কেলার রাশি দুটির মধ্যবর্তী দূরত্ব।যদি চার্জ বিন্দু দুটির গুনফল ধনাত্মক হয়,চার্জ দুটির মধ্যবর্তী বল পরস্পরকে বিকর্ষণ করবে। আর যদি চার্জ বিন্দু দুটির গুনফল ঋণাত্মক হয়, চার্জ দুটির মধ্যবর্তী বল পরস্পরকে আকর্ষণ করবে।[পাশের এই চিত্রটি দেখায় যে অভিন্ন চার্জগুলো একে অপরকে বিকর্ষণ করছে এবং বিপরীত চার্জগুলো একে অপরকে আকর্ষণ করছে।]

The absolute value of the force ${\boldsymbol {F}}$ between two point charges $q$ and $Q$ relates to the distance between the point charges and to the simple product of their charges. The diagram shows that like charges repel each other, and opposite charges attract each other.

ভেক্টর কাঠামো

In the image, the vector ${\boldsymbol {F}}_{1}$ is the force experienced by $q_{1}$, and the vector ${\boldsymbol {F}}_{2}$ is the force experienced by $q_{2}$. When $q_{1}q_{2}>0$ the forces are repulsive (as in the image) and when $q_{1}q_{2}<0$ the forces are attractive (opposite to the image). The magnitude of the forces will always be equal.

ভেক্টর কাঠামো অনুযায়ী স্থির তড়িৎ বল ${\boldsymbol {F}}_{1}$ দারা অনুভুত হয় চার্জ,$q_{1}$ এর অবস্থান ${\boldsymbol {r_{1}}}$।আবার,$q_{2}$ এর অবস্থান ${\boldsymbol {r_{2}}}$ হলে ${\boldsymbol {F_{1}}}={q_{1}q_{2} \over 4\pi \varepsilon _{0}}{({\boldsymbol {r_{1}-r_{2}}}) \over |{\boldsymbol {r_{1}-r_{2}}}|^{3}}={q_{1}q_{2} \over 4\pi \varepsilon _{0}}{{\boldsymbol {{\hat {r}}_{12}}} \over |{\boldsymbol {r_{12}}}|^{2}},$

যেখানে ${\boldsymbol {r_{12}}}={\boldsymbol {r_{1}-r_{2}}}$,একক ভেক্টর ${\boldsymbol {{\hat {r}}_{12}}}={{\boldsymbol {r_{12}}}/|{\boldsymbol {r_{12}}}|}$,এবং $\varepsilon _{0}$ হল তড়িৎ ধ্রুবক।[নিচের ছবিতে ভেক্টর বল ${\boldsymbol {F}}_{1}$,$q_{1}$এর উপর ক্রিয়া করে।${\boldsymbol {F}}_{2}$ বল $q_{2}$ এর উপর ক্রিয়া করে।যখন $q_{1}q_{2}>0$ তখন বলগুলো পরস্পরকে বিকর্ষণ করবে এবং $q_{1}q_{2}<0$তখন বলগুলো পরস্পরকে আকর্ষণ করবে।] ভেক্টর কাঠামোর ব্যাখ্যা স্কেলার কাঠামোর মতই কিন্তু এতি একটি একক ভেক্টর ${\boldsymbol {{\hat {r}}_{12}}}$ এবং সমান্তরাল চার্জ $q_{2}$ হতে $q_{1}$ পর্যন্ত।যদি উভয় চার্জ এর চিহ্ন অভিন্ন হয় তবে তাদের গুনফল ধনাত্মক হবে এবং $q_{1}$ এর উপর বলের দিক হবে ${\boldsymbol {{\hat {r}}_{12}}}$এবং চার্জগুলো একে অপরকে বিকর্ষণ করবে।যদি উভয় চার্জ এর চিহ্ন ভিন্ন হয় তবে তাদের গুনফল ঋণাত্মক হবে,$q_{1}$ এর উপর বলের দিক হবে $-{\boldsymbol {{\hat {r}}_{12}}}$; এবং তখন চার্জগুলো পরস্পরকে আকর্ষণ করবে।স্থির তড়িৎ বল ${\boldsymbol {F_{2}}}$,$q_{2}$দারা অনুভুত হবে।নিউটনের ৩য় সুত্রানুসারে, ${\boldsymbol {F_{2}}}=-{\boldsymbol {F_{1}}}$

পৃথক চার্জ এর পদ্ধতি

উপরিপাতনের নীতি কুলম্বের সূত্রকে যে কোনো বিন্দু চার্জ এর অন্তর্ভুক্ত করতে অনুমোদন করে।বিন্দু চার্জ এর পদ্ধতি অনুসারে বল বিন্দু চার্জ এর উপর ক্রিয়া করে।একক বলের জন্য বিন্দু চার্জ সাধারনত ভেক্টর যোগ হয়।তড়িৎ ক্ষেত্রের বিন্দুতে ভেক্টর বল সমান্তরাল যেখানে বিন্দু চার্জ অপসারন করা হয়ে থাকে।বল ${\boldsymbol {F}}$ এর উপর ক্ষুদ্র চার্জ $q$ যার অবস্থান ${\boldsymbol {r}}$ এবং চার্জ পৃথকীকরণ $N$ শূন্যর মধ্যে হলে :${\boldsymbol {F(r)}}={q \over 4\pi \varepsilon _{0}}\sum _{i=1}^{N}q_{i}{{\boldsymbol {r-r_{i}}} \over |{\boldsymbol {r-r_{i}}}|^{3}}={q \over 4\pi \varepsilon _{0}}\sum _{i=1}^{N}q_{i}{{\boldsymbol {\widehat {R_{i}}}} \over |{\boldsymbol {R_{i}}}|^{2}},$ যেখানে $q_{i}$ এবং ${\boldsymbol {r_{i}}}$ হল আপেক্ষিকভাবে $i^{th}$চার্জএর মান এবং অবস্থান। ${\boldsymbol {\widehat {R_{i}}}}$হল একক ভেক্টর যেখানে ${\boldsymbol {R}}_{i}={\boldsymbol {r}}-{\boldsymbol {r}}_{i}$ (ভেক্টর বিন্দুর $q_{i}$ হতে $q$)

ধারাবাহিক চার্জ পদ্ধতি

এই ক্ষেত্রে রৈখিক উপরিপাতন এর নীতি ব্যবহৃত হয়। ধারাবাহিক চার্জ বণ্টনের ক্ষেত্রে,এক খণ্ড চার্জ অঞ্চলের উপর যে পরিমান চার্জ বহন করে তা অসীম যোগফলের সমান $dq$ ক্ষুদ্রাতিক্ষুদ্র চার্জ এর মত আচারন করে।সাধারনত রৈখিক চার্জ বণ্টনের ক্ষেত্রে,পৃষ্ঠ অথবা আয়তনের সাহায্য পরিমাপ সংক্রান্ত।

রৈখিক চার্জ বণ্টনের ক্ষেত্রে (প্রায় ভাল চার্জ এর একটা তার)যেখানে $\lambda ({\boldsymbol {r'}})$প্রতিটি দৈর্ঘ্য এককে চার্জ দেয় ${\boldsymbol {r'}}$ এবং $dl'$ হল ক্ষুদ্রাতিক্ষুদ্র চার্জ দৈর্ঘ্য

$dq=\lambda ({\boldsymbol {r'}})dl'$.

পৃষ্ঠীয় চার্জ বণ্টনের ক্ষেত্রে(একটি সমান্তরাল বর্তনীতে প্রায় ভাল চার্জ)যেখানে $\sigma ({\boldsymbol {r'}})$প্রতি একক চার্জ দেয় এবং অবস্থান ${\boldsymbol {r'}}$।$dA'$ক্ষুদ্রাতিক্ষুদ্র চার্জ আয়তন :

$dq=\sigma ({\boldsymbol {r'}})\,dA'.$

চার্জ এর আয়তন বণ্টনের ক্ষেত্রে(চার্জ ভারি বস্তুর মধ্যে)যেখানে $\rho ({\boldsymbol {r'}})$প্রতি একক আয়তনে চার্জ দেয় এবং অবস্থান ${\boldsymbol {r'}}$, $dV'$ক্ষুদ্রাতিক্ষুদ্র চার্জ আয়তন হল

$dq=\rho ({\boldsymbol {r'}})\,dV'.$

একটি ছোট চার্জ $q'$ এর অবস্থান ${\boldsymbol {r}}$ হলে শূনের মধ্যে বল :${\boldsymbol {F}}={q' \over 4\pi \varepsilon _{0}}\int dq{{\boldsymbol {r}}-{\boldsymbol {r'}} \over |{\boldsymbol {r}}-{\boldsymbol {r'}}|^{3}}.$

কুলম্বের সূত্রের সত্যতা পরীক্ষা

Experiment to verify Coulomb's law.

একটি সহজ পরীক্ষা দ্বারা কুলম্বের সূত্রের সত্যতা যাচাই করা যায়।ধরা যাক,$m$ভরের দুটি গোলক নেয়া হল,তাদের সমান চার্জ $q$ সমান দূরত্ব $l$ এই গোলকের উপর তিন ধরনের বল কাজ করে,ওজন $mg$ রশির টান $T$ তড়িৎ বল ${\boldsymbol {F}}$।এই সাম্য অবস্থানে

$T\ \sin \theta _{1}=F_{1}\,\!$ ********(১)

এবং

$T\ \cos \theta _{1}=mg\,\!$ ********(২)

সমীকরণ ১ কে ২ দ্বারা ভাগ করে,

${\frac {\sin \theta _{1}}{\cos \theta _{1}}}={\frac {F_{1}}{mg}}\Rightarrow F_{1}=mg\tan \theta _{1}$

গোলকের চার্জ এর মধ্যে দূরত্ব $L_{1}\,\!$ এবং তাদের বিকর্ষণ বল $F_{1}\,\!$।ধরি,কুলম্বের সূত্র নির্ভুল এবং এটি

$F_{1}={\frac {q^{2}}{4\pi \epsilon _{0}L_{1}^{2}}}$

এবং

${\frac {q^{2}}{4\pi \epsilon _{0}L_{1}^{2}}}=mg\tan \theta _{1}\,\!$

এখন আমরা যদি যেকোনো একটি গোলককে চার্জ মুক্ত করি এবং যদি এটাকে চার্জ গোলকে রাখি তখন প্রতিটি চার্জ চার্জ q/2 অর্জন করবে। এই অবস্থায় হবে চার্জ এর মধ্যেবর্তি দূরত্ব এবং বিকর্ষণ বল হবে

$F_{2}={\frac {{(q/2)}^{2}}{4\pi \epsilon _{0}L_{2}^{2}}}={\frac {q^{2}/4}{4\pi \epsilon _{0}L_{2}^{2}}}\,\!$

আমরা জানি,$F_{2}=mg.\tan \theta _{2}\,\!$ *******(৩)

এবং ${\frac {\frac {q^{2}}{4}}{4\pi \epsilon _{0}L_{2}^{2}}}=mg.\tan \theta _{2}$ ******(৪)

৩ কে ৪ দারা ভাগ করি, ${\frac {\left({\cfrac {q^{2}}{4\pi \epsilon _{0}L_{1}^{2}}}\right)}{\left({\cfrac {q^{2}/4}{4\pi \epsilon _{0}L_{2}^{2}}}\right)}}={\frac {mg\tan \theta _{1}}{mg\tan \theta _{2}}}\Longrightarrow 4{\left({\frac {L_{2}}{L_{1}}}\right)}^{2}={\frac {\tan \theta _{1}}{\tan \theta _{2}}}$ *******(৫)

কোণ $\theta _{1}\,\!$,$\theta _{2}\,\!$ এবং চার্জ এর মধ্যে দূরত্ব $L_{1}\,\!$ and $L_{2}\,\!$ সমান প্রমাণ এর জন্য যথেষ্ট।পরীক্ষা ভুলের একটা হিসাব রাখতে হবে।অনুশীলনের ক্ষেত্রে কোণের মান বের করা বেশ কঠিন,যদি রাশির দৈর্ঘ্য বেশ বড় নেই তবে কর্ণের মান প্রায় ছোট হবে,

$\tan \theta \approx \sin \theta ={\frac {\frac {L}{2}}{l}}={\frac {L}{2l}}\Longrightarrow {\frac {\tan \theta _{1}}{\tan \theta _{2}}}\approx {\frac {\frac {L_{1}}{2l}}{\frac {L_{2}}{2l}}}$ **********(৬)

এই সম্ভাব্য সম্পর্ক কাজে লাগিয়ে সমীকরণ ৫ কে আরও সহজে লিখা যায়,

${\frac {\frac {L_{1}}{2l}}{\frac {L_{2}}{2l}}}\approx 4{\left({\frac {L_{2}}{L_{1}}}\right)}^{2}\Longrightarrow \,\!$ ${\frac {L_{1}}{L_{2}}}\approx 4{\left({\frac {L_{2}}{L_{1}}}\right)}^{2}\Longrightarrow {\frac {L_{1}}{L_{2}}}\approx {\sqrt[{3}]{4}}\,\!$

এইভাবে চার্জ এর দূরত্ব সত্যতা যাচাই করাটা সীমিত এবং ভাগ করা সম্ভাব্য তত্ত্ব দেখতে হবে।

প্রসারণ এর অসীম গতির পরীক্ষামূলক প্রমাণ

২০১২ সালের শেষের দিকে ‘ইষ্টিটুটো নাজিওনাল ডি ফিসিকা নিউক্লিয়ারের’ গবেষকরা রোমের ফ্রেস্কাটির এর ‘ল্যাবরেটরি নাজিওনাল ডি ফিসিকাটি’ তে একটি পরীক্ষা করেন। সেখানে তারা চিহ্নিত করেন যে,ইলেকট্রন এর কিরণ এবং আবিষ্কারক যন্ত্রের মধ্যে বলের প্রসারণএ কোন বিলম্ব হয় নি।এটা চিহ্নিত করাছিল যে, ইলেকট্রন এর কিরণ বা আলোকরশ্মি ক্ষেত্রটির সাথে ভ্রমণ করে যেন পূর্ববর্তী আলোকরশ্মিগুলোর গঠন দৃঢ় হয়।যদিও প্রত্যাশিত প্রতিপাদন এর ফলাফল চিহ্নিত করে যে,সাময়িক স্মৃতিভ্রংশ কুলম্বের বলে উপস্থিত ছিল না।

স্থিরতড়িৎ এর আসন্ন মান

অন্য সূত্রে দেখা যায় যে, কুলম্বের সূত্র পুরোপুরি নির্ভুল যখন বস্তুগুলো স্থির এবং যখন প্রায়ই ধীর গতিতে থাকে তখন প্রায় নির্ভুল। এই অবস্থাগুলোকে স্থির তড়িৎ এর আসন্ন বলে। যখন গতিবিধির ফলে স্থান দখল করে তখন তড়িৎ চুম্বক ক্ষেত্র যা পরিবর্তিত বলের প্রভাবে বস্তু দুটির মধ্যে উৎপন্ন হয়।গতিসম্পন্ন চার্জগুলোর মধ্যেবর্তী চুম্বকীয় আকর্ষণকে স্থির তড়িৎ ক্ষেত্রে বলের ঘটনা মনে করা হয়। কিন্তু আইনস্টাইনের আপেক্ষিক তত্ত্বের সাথেও একে বিবেচনা করা হয়। অন্যান্য তত্ত্ব যেমন ওয়েবার এর ইলেকট্রো ডায়নামিক বলে যে অন্যান্য গতি কুলম্বের সূত্র এর সংশোধনের উপর নির্ভরশীল।

পারমাণবিক বল

কুলম্বের সূত্র এর ব্যবহার পরমাণুর মধ্যেও আছে। পারমাণবিক নিউক্লিয়াস এর ধনাত্মক চার্জ এবং ইলেকট্রনের প্রতিটি ঋণাত্মক চার্জ এর মধ্যবর্তী বলকে নির্ভুলভাবে ব্যাখ্যা করতে এটি ব্যবহৃত হয়। অণু হতে পরমাণুকে একত্রে আলাদা করা কঠিন ও তরল হতে অণু, পরমাণুকে একত্রীকরণে এই সহজ সূত্রটি দারা নির্ভুলভাবে হিসাব পাওয়া যায়। সাধারণত, যেহেতু আয়ন এর মাঝে দূরত্ব বৃদ্ধি পাওয়া, আকর্ষণ শক্তি শুন্যের কাছাকাছি এবং আয়নিক বন্ধন কম সহায়ক। যেহেতু, বিপরীত চার্জ এর মান বৃদ্ধি, শক্তি বৃদ্ধি এবং আয়নিক বন্ধন অনেক সুবিধাপূর্ণ।