চৌম্বক ফ্লাক্স
| তড়িৎচুম্বকত্ব |
|---|
| সম্পর্কিত নিবন্ধ |
 |
এই নিবন্ধে তথ্যসূত্রের একটি তালিকা রয়েছে, কিন্তু উক্ত তালিকায় পর্যাপ্ত সংগতিপূর্ণ উদ্ধৃতির অভাব বিদ্যমান। (অক্টোবর ২০২০) |
পদার্থবিজ্ঞানে, বিশেষত তড়িচ্চুম্বকত্বে, কোনো তলের চৌম্বক ফ্লাক্স ( Φ বা ΦB দ্বারা প্রকাশিত) হলো, ঐ তলের লম্ব বরাবর, তলের ভেতর দিয়ে প্রবাহিত চৌম্বক ক্ষেত্রের ফ্লাক্স ঘনত্ব B এর উপাংশের তল সমাকলন (সারফেস ইন্টিগ্রাল)। চৌম্বক ফ্লাক্সের এসআই একক হলো ওয়েবার (Wb; আহরিত একক ভোল্ট-সেকেন্ড), এবং সিজিএস একক হলো ম্যাক্সওয়েল। চৌম্বক ফ্লাক্স সাধারণত ফ্লাক্সমিটার দিয়ে পরিমাপ করা হয়, যা এর ভেতরে থাকা কুন্ডলীর বিভব পরিবর্তন হিসাব করে চৌম্বক ফ্লাক্স গণনা করে। ১০ ওয়েবার চৌম্বক ফ্লাক্স বলতে বোঝায় কোনো কুন্ডলীর ক্ষেত্রফল ১ বর্গ মিটার হলে কুন্ডলীর তলের লম্ব বরাবর চৌম্বকক্ষেত্রের উপাংশ ১০ টেসলা। (1 Wb=1 Tm²)
বিবরণ[সম্পাদনা]
চৌম্বকীয় মিথস্ক্রিয়া ভেক্টর ক্ষেত্রের সাপেক্ষে বর্ণনা করা হয়, যেখানে প্রত্যেকটি বিন্দুকে একটি ভেক্টর মান দেওয়া হয়, যা নির্ধারণ করে কোনো গতিশীল আধান ঐ বিন্দুতে কি পরিমাণ বল অনুভব করবে (লরেঞ্জ বল দেখুন)।[১] যেহেতু শুরুতে একটি ভেক্টর ক্ষেত্র কল্পনা করা বেশ কঠিন, তাই প্রাথমিক পদার্থবিদ্যায় বলরেখা দ্বারা এই ক্ষেত্রটি কল্পনা করা হয়। এই সরলীকৃত চিত্রে, কিছু কিছু তলের ক্ষেত্রে, চৌম্বক ফ্লাক্স ঐ তলের মধ্য দিয়ে অতিক্রান্ত বলরেখার সংখ্যার সমানুপাতিক (কিছু ক্ষেত্রে, চৌম্বক ফ্লাক্সকে নির্দিষ্টভাবে ঐ তলের মধ্য দিয়ে অতিক্রান্ত বলরেখার সংখ্যার সমান হিসেবে সংজ্ঞায়িত করা হতে পারে; যদিও আসলে এটি বিভ্রান্তিকর তবুও এই প্রভেদ ততটা গুরুতর নয়)। চৌম্বক ফ্লাক্স হলো ঐ তলের মধ্য দিয়ে অতিক্রান্ত বলরেখার নিট সংখ্যা; অর্থাৎ একদিকে প্রবাহিত বলরেখা ও তার বিপরীত দিকে প্রবাহিত বলরেখার বিয়োগফল (বলরেখা কোনদিকে ধনাত্মক আর কোনদিকে ঋণাত্মক হবে তা জানার জন্য নিচে দেখুন)[২]। উচ্চতর পদার্থবিদ্যায়, বলরেখার রূপায়নটি প্রত্যাখ্যান করা হয় এবং চৌম্বক ফ্লাক্স সঠিকভাবে, কোনো তলের লম্ব বরাবর, এর ভেতর দিয়ে প্রবাহিত চৌম্বক ক্ষেত্রের ফ্লাক্স ঘনত্বের উপাংশের সমাকলন হিসেবে সংজ্ঞায়িত করা হয়। যদি চৌম্বক ক্ষেত্র ধ্রুবক হয় তবে, ভেক্টর ক্ষেত্র S এর মধ্য দিয়ে প্রবাহিত চৌম্বক ফ্লাক্স,


যেখানে B হলো চৌম্বক ক্ষেত্রের মাত্রা (চৌম্বক ফ্লাক্স ঘনত্ব), যার একক হলো Wb/m2 (টেসলা), S হলো তলের ক্ষেত্রফল এবং θ হলো S বরাবর লম্বরেখা ও চৌম্বক বলরেখার মধ্যবর্তী কোণ। পরিবর্তনশীল চৌম্বকক্ষেত্রের জন্য, আমরা প্রথমে অসীম সংখ্যক ক্ষুদ্র অংশ dS কে বিবেচনা করি, যার চৌম্বকক্ষেত্র স্থির বলে ধরা যেতে পারে:
অর্থাৎ, একটি পূর্ণাঙ্গ তল S অসীম সংখ্যক ক্ষুদ্র অংশে বিভক্ত করা যায়, এবং ঐ তলের চৌম্বক ফ্লাক্স হবে এদের সমাকলন এর সমান:
চৌম্বক ভেক্টর বিভব A এর সংজ্ঞা থেকে এবং কার্ল এর মৌলিক উপপাদ্য থেকে এভাবেও চৌম্বক ফ্লাক্স সংজ্ঞায়িত করা যায়:
যেখানে ∂S হিসেবে বর্ণিত, S তলের সীমানা দিয়ে রৈখিক সমাকলন করা হয়।
বদ্ধ তলের ভেতর দিয়ে চৌম্বক ফ্লাক্স[সম্পাদনা]

গাউসের চুম্বকত্বের সূত্র, যা ম্যাক্সওয়েলের সমীকরণ চারটির মধ্যে অন্যতম, বলে যে, বদ্ধ তলের ভেতর দিয়ে প্রবাহিত চৌম্বক ফ্লাক্সের মান ০ (বদ্ধ তল হলো এমন তল যা কোনো ছিদ্র ব্যতীত কোনো স্থান পরিপূর্ণভাবে আবদ্ধ করে রাখে)। এককপোল বিশিষ্ট চৌম্বক (ম্যাগনেটিক মনোপোল) কখনও খুঁজে পাওয়া যায়নি, এই পর্যবেক্ষণের ওপর ভিত্তি করে সূত্রটি তৈরী হয়েছে।
সোজা কথায়, গাউসের চুম্বকত্বের সূত্রের বিবৃতি হলো:
যেকোনো বদ্ধ তল S এর জন্য।
উন্মুক্ত তলের ভেতর দিয়ে চৌম্বক ফ্লাক্স[সম্পাদনা]
বদ্ধ তলের ভেতর দিয়ে প্রবাহিত চৌম্বক ফ্লাক্সের মান সর্বদা শূন্য হলেও, উন্মুক্ত তলের ক্ষেত্রে তা বাধ্যতামূলকভাবে শূন্য নয় এবং তড়িচ্চুম্বকত্বে এটি একটি গুরুত্বপূর্ণ পরিমাপ।
কোনো তলের মোট চৌম্বক ফ্লাক্স নির্ণয়ের সময় শুধুমাত্র তলের সীমানা নির্ধারণ করতে হয়, তলটির প্রকৃত আকার এখানে অপ্রাসঙ্গিক এবং একই সীমানা বিশিষ্ট তলের সমাকলন সমানই হবে। এটি বদ্ধ তলের চৌম্বক ফ্লাক্স ০ হওয়ার স্পষ্ট ফলাফল।
পরিবর্তনশীল চৌম্বক ফ্লাক্স[সম্পাদনা]
উদাহরণস্বরূপ, তড়িৎবাহী তারের মধ্য দিয়ে প্রবাহিত চৌম্বক ফ্লাক্সের মানে পরিবর্তন করা হলে কুন্ডলীতে তড়িচ্চালক শক্তি তথা তড়িৎ প্রবাহ তৈরী হবে। এই সম্পর্কটি ফ্যারাডের সূত্রে বিবৃত:
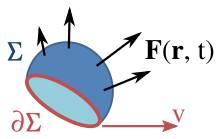
যেখানে,
- হলো তড়িচ্চালক শক্তি
- ΦB হলো উন্মুক্ত তল Σ এর ভেতর দিয়ে প্রবাহিত চৌম্বক ফ্লাক্স
- ∂Σ হলো উন্মুক্ত তল Σ এর সীমানা ; তলটি সাধারণত গতিশীল এবং বিক্ররত হতে পারে, আর তাই এটি সময়ের একটি ফাংশন। তড়িচ্চালক শক্তি এই সীমানা বরাবর আবিষ্ট হয়।
- dℓ হলো ∂Σ সীমানার ক্ষুদ্রাংশ
- v হলো সীমানা ∂Σ এর বেগ
- E হলো তড়িৎ ক্ষেত্র
- B হলো চৌম্বক ক্ষেত্র

তড়িচ্চালক শক্তির জন্য সমীকরণ দুটি হলো, প্রথমত, (সম্ভবত চলমান) তলের সীমানা জুড়ে একটি পরীক্ষাধীন চার্জ সরিয়ে নিতে লরেঞ্জ বলের বিরুদ্ধে প্রতি একক আধানে কৃতকাজ এবং দ্বিতীয়ত, উন্মুক্ত তল Σ এর ভেতর দিয়ে চৌম্বক ফ্লাক্সের পরিবর্তন হিসেবে। এই সমীকরণটি বৈদ্যুতিক জেনারেটর তৈরীর মূলনীতি।
তড়িৎ ফ্লাক্সের সাথে তুলনা[সম্পাদনা]
বিপরীত ভাবে, ম্যাক্সওয়েলের সমীকরণের আরেকটি, তড়িৎ ক্ষেত্রের জন্য গাউসের সূত্র:
যেখানে,
- E হলো তড়িৎ ক্ষেত্র
- S যেকোনো বদ্ধ তল
- Q হলো S তলের অভ্যন্তরে মোট বৈদ্যুতিক আধান
- ε0 হলো একটি সার্বিক ধ্রুবক (শূন্যস্থানের প্রবেশ্যতা)
বদ্ধ তলে E এর ফ্লাক্স সর্বদা শূন্য নয়, যা তড়িৎ একক আধানের অর্থাৎ মুক্ত ধনাত্মক বা ঋণাত্মক আধানের অস্তিত্ব নিশ্চিত করে।
আরও দেখুন[সম্পাদনা]
- চৌম্বক বর্তনী হলো একটি বদ্ধ পথ যাতে চৌম্বক ফ্লাক্স প্রবাহিত হয়
- চৌম্বক ফ্লাক্স কোয়ান্টাম
- ফ্লাক্স সংযোগ, চৌম্বক ফ্লাক্সের ধারনার সম্প্রসারণ
তথ্যসূত্র[সম্পাদনা]
- ↑ Purcell, Edward and Morin, David (২০১৩)। Electricity and Magnetism (3rd সংস্করণ)। New York: Cambridge University Press। পৃষ্ঠা 278। আইএসবিএন 978-1-107-01402-2।
- ↑ Browne, Michael (২০০৮)। Physics for Engineering and Science (2nd সংস্করণ)। McGraw-Hill/Schaum। পৃষ্ঠা 235। আইএসবিএন 978-0-07-161399-6।
বহিঃসংযোগ[সম্পাদনা]
- US 6720855, Vicci, "Magnetic-flux conduits", ইস্যু করা হয়েছে 2003
- Magnetic Flux through a Loop of Wire আর্নেস্ট লি কর্তৃক লিখিত, Wolfram Demonstrations Project.
- Conversion Magnetic flux Φ in nWb per meter track width to flux level in dB – Tape Operating Levels and Tape Alignment Levels
- wikt:magnetic flux











