ফ্লাক্স

এই নিবন্ধটি প্রাকৃতিক বিজ্ঞান এবং গণিতে ফ্লাক্সের ধারণা সম্পর্কে। অন্য ব্যবহারের জন্য ফ্লাক্স (দ্ব্যর্থতা নিরসন) দেখুন।

ভেক্টর ক্ষেত্র F প্রতি একক ক্ষেত্রফলের মধ্য দিয়ে প্রবাহিত ক্ষেত্র রেখা লম্ব বরাবর n, nথেকে F পর্যন্ত কোণ হলো θ. একটি প্রদত্ত ক্ষেত্রফলের মধ্য দিয়ে কি পরিমাণ ক্ষেত্র গেছে ফ্লাক্স হলো তার পরিমাণ। F কে n এর লম্ব বরাবর (⊥) এবং সমান্তরাল ( ‖ ) বরাবর দুই ভাগে বিভক্ত করা হয়। কেবল সমান্তরাল উপাদানটি ফ্লাক্সে অবদান রাখে, কারণ এটি কোনও বিন্দুতে পৃষ্ঠের উপর দিয়ে যাওয়া ক্ষেত্রের সর্বাধিক পরিমাণ, লম্ব অংশটি তাতে অবদান রাখে না। শীর্ষ: সমতল পৃষ্ঠের মধ্য দিয়ে তিনটি ক্ষেত্র রেখা, একটি তল থেকে লম্ব বরাবর , একটি সমান্তরাল এবং একটি মধ্যবর্তী। তলদেশ: বক্রাকার পৃষ্ঠের মধ্য দিয়ে ক্ষেত্র রেখা, ফ্লাক্স গণনা করার জন্য একক লম্ব ভেক্টর এবং পৃষ্ঠতলের উপাদানসমূহের গঠনকাঠামো দেখায়।

একটি ভেক্টর ক্ষেত্র $\mathbf {F}$ (লাল তীর) এর ফ্লাক্স গণনা করা জন্য এর পৃষ্ঠতল $S$কে ছোট ছোট অংশ $dS$ এ বিভক্ত করা হয়েছে । প্রতিটি অংশের মধ্যে প্রবাহিত ফ্লাক্সের মান ক্ষেত্র এর লম্ব উপাংশের সমান, $\mathbf {F} \cdot \mathbf {n} dS$ যা পৃষ্ঠতলের প্রতিটি অংশের জন্য পৃষ্ঠতলের মধ্য দিয়ে অতিক্রান্ত ফ্লাক্স এর পরিমাণ নির্দেশ করে । $\mathbf {x}$ বিন্দুতে $dS$ $dS$ ক্ষেত্র দ্বারা গুণ করে $\mathbf {F} (\mathbf {x} )$ এর সাথে লম্ব একক ভেক্টর $\mathbf {n} (\mathbf {x} )$ (নীল তীরগুলো) স্কেলার গুণন নির্ণয় করা হয় । প্রতিটি ক্ষুদ্র অংশের জন্য পৃষ্ঠতলের উপর $\mathbf {F} \cdot \mathbf {n} dS$ এর যোগফল ঐ পৃষ্ঠতলের মধ্য দিয়ে অতিক্রান্ত ফ্লাক্স নির্দেশ করে।

ফ্লাক্স হলো এমন এক ধরনের প্রভাব যা কোনও তল বা পদার্থের মধ্য দিয়ে অতিক্রম বা যাতায়াত অবস্থায় (বাস্তবে তা চালিত হোক বা না হোক) প্রদর্শিত হয় । ফ্লাক্স ফলিত গণিত এবং ভেক্টর ক্যালকুলাসের একটি ধারণা যার পদার্থবিজ্ঞানে অনেক প্রয়োগ রয়েছে। পরিবহন ঘটনার জন্য, ফ্লাক্স একটি ভেক্টর রাশি, যা কোনও পদার্থ বা বস্তুর প্রবাহের পরিমাণ এবং দিক নির্দেশ করে। ভেক্টর ক্যালকুলাসে ফ্লাক্স একটি স্কেলার রাশি, ভেক্টর ক্ষেত্রের লম্ব অংশসমূহের পৃষ্ঠতলের ব্যবকলন দ্বারা সংজ্ঞায়িত করা হয়।

পরিভাষা

ফ্লাক্স শব্দটি লাতিন শব্দ ফ্লাক্সাস এবং ফ্লুইর থেকে এসেছে : এদের অর্থ যথাক্রমে 'প্রবাহিত' এবং 'প্রবাহিত হওয়া'। আইজ্যাক নিউটন ফ্লাক্সিয়ন নামটি প্রথম ডিফারেন্সিয়াল ক্যালকুলাস এ ব্যবহার করে।

তাপ স্থানান্তর ঘটনার বিশ্লেষণে তাপ ফ্লাক্সের ধারণা জোসেফ ফুরিয়ে এর মূল অবদান ছিল। তার ধাতুবিষয়ক Théorie analytique de la chaleur (তাপের বিশ্লেষণাত্মক তত্ত্ব ) গ্রন্থে তিনি 'ফ্লাক্সন'কে কেন্দ্রীয় পরিমাণ হিসাবে সংজ্ঞায়িত করেছেন এবং কাচের ফলক জুড়ে তাপমাত্রার পার্থক্যের ক্ষেত্রে ফ্লাক্সের এখনকার সুপরিচিত সমীকরণগুলি অর্জন করতে এগিয়ে কাজ করে গিয়েছেন এবং তারপরে আরও সাধারণভাবে বিবেচনা করা হয় অন্যান্য জ্যামিতি জুড়ে তাপমাত্রার গ্রেডিয়েন্ট বা তাপমাত্রার ডিফারেনশিয়াল সমীকরণ অর্জন করতে এগিয়ে গিয়েছিলেন । জেমস ক্লার্ক ম্যাক্সওয়েলের, কাজের উপর ভিত্তি করে কেউ যুক্তি দিতে পারেন যে পরিবহন সংজ্ঞা তড়িৎ চৌম্বকীয়তায় ব্যবহৃত ফ্লাক্সের সংজ্ঞাটি মধ্যে আগে থেকে রয়েছে। ম্যাক্সওয়েলের নির্দিষ্ট উক্তিটি হলঃ

ফ্লাক্সের ক্ষেত্রে, আমাদের একটি পৃষ্ঠতলের উপরের প্রতিটি অংশের মধ্য দিয়ে অতিক্রান্ত ফ্লাক্সের যোগজীকরণ নিতে হবে। এই অপারেশনের ফলাফলকে বলা হয় ফ্লাক্সের পৃষ্ঠতলের যোগজীকরণ । এটি এমন পরিমাণকে উপস্থাপন করে যা পৃষ্ঠতলের মধ্য দিয়ে যায়।

— জেমস ক্লার্ক ম্যাক্সওয়েল

পরিবহন সংজ্ঞা অনুসারে, ফ্লাক্স একক ভেক্টর হতে পারে, বা এটি কোনও ভেক্টর ক্ষেত্র / অবস্থানের ফাংশন হতে পারে।পরবর্তী ক্ষেত্রে ফ্লাক্স সহজেই একটি পৃষ্ঠতলের উপর একীভূত হতে পারে।বিপরীতে, তড়িৎচুম্বকতত্ত্বের সংজ্ঞা অনুযায়ী ফ্লাক্স কোন পৃষ্ঠতলের উপর যোগজীকরণ হয়;। ফ্লাক্স এর দ্বিতীয় সংজ্ঞার কোন অর্থই হতে পারে না কারণ, এটি একটি পৃষ্ঠতলের উপর দুইবার যোগজীকরণকে বোঝায় ।সুতরাং, ম্যাক্সওয়েলের উদ্ধৃতিটি কেবল তখনই বোধগম্য হয় যদি "ফ্লাক্স" পরিবহন সংজ্ঞা অনুসারে ব্যবহৃত হয় (এবং তদুপরি একক ভেক্টরের পরিবর্তে এটি একটি ভেক্টর ক্ষেত্র )।এটি ব্যঙ্গাত্মক কারণ তড়িৎচুম্বকীয় সংজ্ঞা অনুসারে এখন আমরা যাকে "বৈদ্যুতিক ফ্লাক্স " এবং "চৌম্বকীয় ফ্লাক্স" বলি ম্যাক্সওয়েল তার অন্যতম প্রধান বিকাশকারী ছিলেন ।উদ্ধৃতি (এবং পরিবহন সংজ্ঞা) অনুসারে তাদের নামগুলি হবে "বৈদ্যুতিক ফ্লাক্সের পৃষ্ঠতলের যোগজ" এবং "চৌম্বকীয় ফ্লাক্সের পৃষ্ঠতলের যোগজ", সেই ক্ষেত্রে "বৈদ্যুতিক ফ্লাক্স" এর পরিবর্তে "বৈদ্যুতিক ক্ষেত্র" এবং "চৌম্বকীয় ফ্লাক্স" এর পরিবর্তে "" চৌম্বকীয় ক্ষেত্র " হিসাবে সংজ্ঞায়িত হবে ।এটি সূচিত করে যে, ম্যাক্সওয়েল এই ক্ষেত্রগুলি কোনও প্রকারের প্রবাহ / ফ্লাক্স হিসাবে কল্পনা করেছিলন।

তড়িৎ চুম্বকীয় সংজ্ঞা অনুসারে একটি ফ্লাক্স হলো ,সংশ্লিষ্ট ফ্লাক্স ঘনত্ব , যদি শব্দটি ব্যবহার করা হয়, ,তবে এটি যোগজীকরণকৃত পৃষ্ঠতল বরাবর এর ডেরিভেটিভকে বোঝায় ।ক্যালকুলাসের মৌলিক উপপাদ্য অনুসারে, পরিবহন সংজ্ঞা অনুসারে সংশ্লিষ্ট ফ্লাক্স ঘনত্ব একটি ফ্লাক্স। পরিবহন সংজ্ঞা অনুসারে, বৈদ্যুতিক কারেন্ট — প্রতি একক সময়ে প্রবাহিত চার্জ, তড়িৎ ঘনত্ব(প্রতি একক ক্ষেত্রফলে একক সময়ে প্রবাহিত চার্জের পরিমাণ ) ফ্লাক্স হবে। ফ্লাক্সের দ্বন্দ্বপূর্ণ সংজ্ঞা এবং প্রচলিত বাংলাতে ফ্লাক্স, প্রবাহ এবং তড়িৎ শব্দগুলো একে অপরের পরিবর্তিতে এবং অস্পষ্টভাবে অনুচ্ছেদে ব্যবহৃত হয়েছে।এই নিবন্ধের বাকী অংশে কংক্রিট ফ্লাক্সগুলি সাহিত্যে তাদের বিস্তৃত গ্রহণযোগ্যতা অনুসারে ব্যবহৃত হবে, ফ্লাক্সের যে সংজ্ঞাই শব্দটি বোঝায় না কেন।

প্রতি একক ক্ষেত্রফলে প্রবাহের হার হিসাবে ফ্লাক্স

পরিবহন ঘটনায় ( তাপ স্থানান্তর, ভর স্থানান্তর এবং তরল গতিবিদ্যা ), ফ্লাক্সকে প্রতি একক ক্ষেত্রফলে প্রবাহের হার হিসাবে সংজ্ঞায়িত করা হয়, যার মাত্রা সমীকরণ [পরিমাণ] [সময়] ⁻¹ · [ক্ষেত্র ] ⁻¹ । ক্ষেত্রফল ঐ অঞ্চল যার "মধ্য দিয়ে" বা "জুড়ে" ফ্লাক্স প্রবাহিত হচ্ছে।উদাহরণস্বরূপ, একটি নদীর স্রোতের বিশালতা, অর্থাৎ প্রতিটি সেকেন্ডে নদীর প্রতিটি ক্ষুদ্র অংশের মধ্য দিয়ে প্রবাহিত পানির পরিমাণ অথবা প্রতি সেকেন্ডে একটি ক্ষুদ্র অংশের উপর যে পরিমাণ সৌরশক্তি অবতরণ করে, তা এক হলো ধরনের ফ্লাক্স।

সাধারণ গাণিতিক সংজ্ঞা (পরিবহন)

জটিলতার ক্রম অনুযায়ী এখানে ৩ ধরনের সংজ্ঞা রয়েছে। প্রত্যেকটি নিম্নলিখিতগুলির একটি বিশেষ ঘটনা ।সমস্ত ক্ষেত্রে j, (বা J ) প্রতীক ফ্লাক্সের জন্য , Q ভৌত রাশির জন্য যা প্রবাহিত হয় , সময়ের জন্য t এবং ক্ষেত্রফলের জন্য A ব্যবহার করা হয় । এই শনাক্তকারীরা কেবল তখনই মোটা অক্ষরে লেখা হবে যখন এরা ভেক্টর হিসেবে ব্যবহার করা হয়।

প্রথমত, (একক) স্কেলার হিসাবে প্রবাহ:

$j={\frac {I}{A}}$

যেখানে:

$I=\lim \limits _{\Delta t\rightarrow 0}{\frac {\Delta q}{\Delta t}}={\frac {\mathrm {d} q}{\mathrm {d} t}}$

এক্ষেত্রে যে ক্ষেত্রফলের উপর ফ্লাক্স পরিমাপ করা হচ্ছে ঐ পৃষ্ঠতলটি স্থির থাকবে এবং এর ক্ষেত্রফল হবে A । পৃষ্ঠটি সমতল বলে ধরে নেওয়া হয়, এবং প্রবাহটি অবস্থানের সাথে এবং পৃষ্ঠের লম্বাকৃতির সাথে সর্বত্র ধ্রুবক হিসাবে ধরে নেওয়া হয়।

দ্বিতীয়ত, ফ্লাক্স একটি পৃষ্ঠতলের স্কেলার ক্ষেত্র হিসাবে সংজ্ঞায়িত প্রবাহ, যেমন পৃষ্ঠতলের উপর অবস্থিত বিন্দুগুলির একটি ফাংশন:

$j(\mathbf {p} )={\frac {\partial I}{\partial A}}(\mathbf {p} )$

$I(A,\mathbf {p} )={\frac {\mathrm {d} q}{\mathrm {d} t}}(A,\mathbf {p} )$

আগের মতোই, পৃষ্ঠটি সমতল বলে ধরে নেওয়া হয়েছে, এবং প্রবাহটি এর সর্বত্র লম্ব বলে মনে করা হয়।তবে প্রবাহটি ধ্রুবক হওয়ার দরকার নেই। q পৃষ্ঠতলের উপর অবস্থিত একটি বিন্দু p এর একটি ফাংশন, এবং A, একটি ক্ষেত্র । পৃষ্ঠতলের মধ্য দিয়ে মোট প্রবাহ পরিমাপ করার পরিবর্তে, q তে কেন্দ্র বিশিষ্ট A ক্ষেত্রবিশিষ্ট ডিস্কের মাধ্যমে ফ্লাক্স পরিমাপ করে।

অবশেষে, ভেক্টর ক্ষেত্র হিসাবে ফ্লাক্স:

$\mathbf {j} (\mathbf {p} )={\frac {\partial \mathbf {I} }{\partial A}}(\mathbf {p} )$

$\mathbf {I} (A,\mathbf {p} )={\underset {\mathbf {\hat {n}} }{\operatorname {arg\,max} }}\,\mathbf {\hat {n}} _{\mathbf {p} }{\frac {\mathrm {d} q}{\mathrm {d} t}}(A,\mathbf {p} ,\mathbf {\hat {n}} )$

এই ক্ষেত্রে ফ্লাক্স পরিমাপ করার জন্য কোন নির্দিষ্ট পৃষ্ঠতল নেই । q is a function of a point, an area, and a direction (given by a unit vector, {\displaystyle \mathbf {\hat {n}} }\mathbf {\hat {n}} ), and measures the flow through the disk of area A perpendicular to that unit vector. I is defined picking the unit vector that maximizes the flow around the point, because the true flow is maximized across the disk that is perpendicular to it. The unit vector thus uniquely maximizes the function when it points in the "true direction" of the flow. [Strictly speaking, this is an abuse of notation because the "arg max" cannot directly compare vectors; we take the vector with the biggest norm instead.] আমি ইউনিট ভেক্টরকে বাছাই করে সংজ্ঞায়িত করেছি যা বিন্দুর চারপাশে প্রবাহকে সর্বাধিক করে তোলে, কারণ প্রকৃত প্রবাহটি তার লম্বিত ডিস্ক জুড়ে সর্বাধিক হয়।ইউনিট ভেক্টর এভাবে প্রবাহের "সত্য দিক" নির্দেশ করে যখন অনন্যভাবে ফাংশন সর্বাধিক।[কড়া কথায় বলতে গেলে এটি স্বরলিপিটির অপব্যবহার কারণ "আর্গ সর্বাধিক" সরাসরি ভেক্টরদের তুলনা করতে পারে না; পরিবর্তে আমরা সবচেয়ে বড় আদর্শের সাথে ভেক্টরটি নিই।

সম্পত্তি

এই প্রত্যক্ষ সংজ্ঞাগুলি, বিশেষত শেষগুলি, বরং অনর্থক।উদাহরণস্বরূপ, আরগম্যাক্স নির্মাণটি অভিজ্ঞতাগত পরিমাপের দৃষ্টিকোণ থেকে কৃত্রিম, যখন একটি ওয়েদারভেন বা অনুরূপ কোনও সহজেই একটি বিন্দুতে প্রবাহের দিকটি হ্রাস করতে পারে।ভেক্টর ফ্লাক্সকে সরাসরি সংজ্ঞায়িত করার পরিবর্তে এটি সম্পর্কে কিছু বৈশিষ্ট্য বর্ণনা করা প্রায়শই স্বজ্ঞাত।তদুপরি, এই বৈশিষ্ট্যগুলি থেকে প্রবাহগুলি অনন্যভাবে যাইহোক নির্ধারণ করা যেতে পারে।

If the flux j passes through the area at an angle θ to the area normal $\mathbf {\hat {n}}$, then

$\mathbf {j} \cdot \mathbf {\hat {n}} =j\cos \theta$

যেখানে · নেই ডট পণ্যের ইউনিট ভেক্টর।এই পৃষ্ঠ (অর্থাত এটি স্বাভাবিক) মাধ্যমে সর্দি ক্ষণস্থায়ী উপাদান θ কোসাইন্ ঞ, যখন এলাকা থেকে সর্দি পাসিং স্পর্শিনী এর কম্পোনেন্ট ঞ পাপ θ, কিন্তু কোন সর্দি আসলে স্পর্শিনী এলাকা মাধ্যমে ক্ষণস্থায়ী হয় অভিমুখ.অঞ্চলে স্বাভাবিকভাবে প্রবাহিত প্রবাহের একমাত্র উপাদান হ'ল কোসাইন উপাদান।

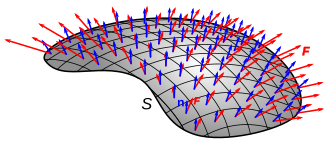
ভেক্টর ফ্লাক্সের জন্য, কোনও সারফেস এস-এর উপরে জের পৃষ্ঠের অবিচ্ছেদ্য, পৃষ্ঠের মধ্য দিয়ে সময়ের প্রতি ইউনিট যথাযথ প্রবাহিত করে।

${\frac {\mathrm {d} q}{\mathrm {d} t}}=\iint _{S}\mathbf {j} \cdot \mathbf {\hat {n}} \,{\rm {d}}A\ =\iint _{S}\mathbf {j} \cdot {\rm {d}}\mathbf {A}$

A (and its infinitesimal) is the vector area, combination of the magnitude of the area through which the property passes, A, and a unit vector normal to the area, $\mathbf {\hat {n}}$. সমীকরণের দ্বিতীয় সেট থেকে ভিন্ন, এখানে পৃষ্ঠতল সমতল হতে হবে না।

অবশেষে, আমরা সময়ের সময়কালে টি ₁ থেকে টি _{2 এর} মধ্যে আবার সংহত করতে পারি, সেই সময় পৃষ্ঠের উপর দিয়ে প্রবাহিত সম্পত্তির মোট পরিমাণ পেয়ে ( টি ₂ - টি ₁ ):

$q=\int _{t_{1}}^{t_{2}}\iint _{S}\mathbf {j} \cdot {\rm {d}}{\mathbf {A} }\,{\rm {d}}t$

পরিবহন ফ্লাক্স

পরিবহন ঘটনা সাহিত্য থেকে প্রবাহের সবচেয়ে প্রচলিত আটটি নিম্নলিখিত হিসাবে সংজ্ঞায়িত করা হয়:

1. গতি প্রবাহ, একটি ইউনিট অঞ্চল জুড়ে গতিবেগ স্থানান্তর হার (N N s · m ^·2 · s ⁻¹ )।( নিউটনের সান্দ্রতা আইন )
2. তাপ প্রবাহ, একক অঞ্চল জুড়ে তাপ প্রবাহের হার (J · m ⁻² · s ⁻¹ )।( বাহন বাহনের আইন ) (তাপ প্রবাহের এই সংজ্ঞাটি ম্যাক্সওয়েলের মূল সংজ্ঞা অনুসারে ফিট করে।
3. ডিফিউশন ফ্লাক্স, একটি ইউনিট অঞ্চল জুড়ে অণুগুলির গতির হার (মোল m এম ⁻² · s ⁻¹ )।( ফিক্সের বিচ্ছুরনের আইন )
4. ভলিউম্যাট্রিক প্রবাহ, একক অঞ্চল জুড়ে ভলিউমের ^{প্রবাহের হার (মি 3} · এম ⁻² · s ⁻¹ )।( ডার্সির ভূগর্ভস্থ জল প্রবাহের আইন )
5. ভর ফ্লাক্স, একক অঞ্চল জুড়ে ভর প্রবাহের হার (কেজি · এম ⁻² · s ⁻¹ )।(হয় ফিকের আইনের একটি বিকল্প রূপ যা আণবিক ভর অন্তর্ভুক্ত করে, বা ডার্সির আইনের একটি বিকল্প রূপ যা ঘনত্বকে অন্তর্ভুক্ত করে।)
6. বিকিরণীয় প্রবাহ, প্রতি সেকেন্ডের ক্ষেত্রের জন্য উৎস থেকে উৎস থেকে নির্দিষ্ট দূরত্বে ফোটন আকারে স্থানান্তরিত শক্তির পরিমাণ ^{(জে এম −2} · s ⁻¹ )।জ্যোতির্বিদ্যায় কোনও তারার দৈর্ঘ্য এবং বর্ণালী শ্রেণি নির্ধারণের জন্য ব্যবহৃত হয়।এছাড়াও তাপ প্রবাহের সাধারণীকরণ হিসাবে কাজ করে যা বৈদ্যুতিন চৌম্বকীয় বর্ণালীতে সীমাবদ্ধ থাকাকালীন রেডিয়েটিভ ফ্লাক্সের সমান।
7. শক্তি প্রবাহ, একক অঞ্চল (J · m ⁻² · s ⁻¹ ) এর মাধ্যমে শক্তি স্থানান্তরের হার।রেডিয়েটিভ ফ্লাক্স এবং হিট ফ্লাক্স শক্তি প্রবাহের নির্দিষ্ট ক্ষেত্রে।
8. কণা প্রবাহ, একক অঞ্চলের মাধ্যমে কণার স্থানান্তরের হার ([কণার সংখ্যা] এম ⁻² · s ⁻¹ )

এই ফ্লাক্সগুলি স্থানের প্রতিটি বিন্দুতে ভেক্টর, এবং একটি নির্দিষ্ট মাত্রা এবং দিক রয়েছে।এছাড়াও, স্থানের একটি নির্দিষ্ট বিন্দুর আশেপাশে নিয়ন্ত্রণের পরিমাণের পরিমাণের পরিমাণ নির্ধারণের জন্য এই প্রবাহগুলির যে কোনও একটির বিভাজন নিতে পারে।অদম্য প্রবাহের জন্য, ভলিউম ফ্লাক্সের বিচ্যুতি শূন্য।

রাসায়নিক বিস্তার

উপরে উল্লিখিত হিসাবে, একটি আইসোথার্মাল, আইসোবারিক সিস্টেমের একটি উপাদান A এর রাসায়নিক গোলার প্রবাহকে ফিকের বিচ্ছুরণের বিধান হিসাবে সংজ্ঞায়িত করা হয়েছে:

$\mathbf {J} _{A}=-D_{AB}\nabla c_{A}$

যেখানে নাবলা প্রতীক grad গ্রেডিয়েন্ট অপারেটরকে বোঝায় , ডি এ _বি উপাদান উপাদান বিয়ের মাধ্যমে বিভাজনকারী উপাদান A এর বিবর্তন সহগ (এম ² · s ⁻¹ ), সি _এ উপাদান উপাদান এ এর ঘনত্ব ( মোল / এম ³

এই প্রবাহটির মোল · এম ⁻² · s ⁻¹ এর ইউনিট রয়েছে এবং ম্যাক্সওয়েলের প্রবাহের মূল সংজ্ঞাটি ফিট করে।

For dilute gases, kinetic molecular theory relates the diffusion coefficient D to the particle density n = N/V, the molecular mass m, the collision cross section $\sigma$, and the absolute temperature T by

$D={\frac {2}{3n\sigma }}{\sqrt {\frac {kT}{\pi m}}}$

যেখানে দ্বিতীয় ফ্যাক্টরটি গড় মুক্ত পথ এবং বর্গমূল ( বোল্টজমানের ধ্রুবক কে সহ ) কণার গড় গতিবেগ।

অশান্ত প্রবাহে, এডি মোশনের মাধ্যমে পরিবহনটি একটি বৃহত্তর বর্ধিত প্রসার সহগ হিসাবে প্রকাশ করা যেতে পারে।

কোয়ান্টাম বলবিজ্ঞান

ইন কোয়ান্টাম বলবিজ্ঞান, এ ভর মি কণা কোয়ান্টাম রাষ্ট্র ψ (R, T) একটি আছে সম্ভাব্যতা ঘনত্ব হিসেবে সংজ্ঞায়িত করা

$\rho =\psi ^{*}\psi =|\psi |^{2}.\,$

সুতরাং ডিফারেন্সিয়াল ভলিউম উপাদান ডি ³ আর এর মধ্যে একটি কণা খুঁজে পাওয়ার সম্ভাবনা is

${\rm {d}}P=|\psi |^{2}{\rm {d}}^{3}\mathbf {r} .\,$

তারপরে প্রতিটি ইউনিট সময়কালের একটি ক্রস-সেকশনের ইউনিট ক্ষেত্রের মধ্য দিয়ে লম্বভাবে কণার সংখ্যা প্রবাহিত সম্ভাবনা;

$\mathbf {J} ={\frac {i\hbar }{2m}}\left(\psi \nabla \psi ^{*}-\psi ^{*}\nabla \psi \right).\,$

এটি কখনও কখনও সম্ভাব্যতা বর্তমান বা বর্তমান ঘনত্ব, বা সম্ভাব্যতা ফ্লাক্স ঘনত্ব হিসাবে পরিচিত।