ডায়নামো তত্ত্ব

পদার্থবিদ্যা অনুসারে ডায়নামো তত্ত্ব হলো এমন প্রক্রিয়া, যার মাধ্যমে কোন অপার্থিব জিনিস যেমন পৃথিবী বা তারকারাজি চৌম্বকীয় ক্ষেত্র তৈরি করে। ডায়নামো তত্ত্ব বর্ণনা করে, যে প্রক্রিয়ায় ঘূর্ণনশীল, পরিচলনরত এবং বিদ্যুৎ পরিবাহী কোন তরল সৌর সময়ের মধ্যে একটি চৌম্বক ক্ষেত্র বজায় রাখে। এই ডায়নামো তত্ত্বকেই পৃথিবীর চৌম্বক ক্ষেত্র সহ দীর্ঘকায় জোভিয়ান গ্রহপুঞ্জ, পারদ এগুলোর চৌম্বকক্ষেত্রের উৎস হিসেবে বর্ণনা করা হয়।

তত্ত্বের ইতিহাস[সম্পাদনা]

১৬০০ সালে ইংরেজ বিজ্ঞানী উইলিয়াম গিলবার্ট যখন তার ডি ম্যাগনেট প্রকাশ করেছিলেন তখন তিনি উপসংহারে এসেছিলেন যে, পৃথিবী চৌম্বকীয়। তিনি অনুমান করেছিলেন, এই চৌম্বকত্বের উৎস হলো আয়োডোস্টোনের মতোই স্থায়ী চুম্বক। ১৯১৯ সালে জোসেফ লারমোর প্রস্তাব দিয়েছিলেন, কোনও ডায়নামো এই চোম্বকক্ষেত্রটি তৈরি করছে।^[২]^[৩] যাইহোক, তিনি তার প্রস্তাবনাকে আরো উন্নত করার পরেও তৎকালীন কিছু বিশিষ্ট বিজ্ঞানী বিকল্প ব্যাখ্যা নিয়েই কাজ করছিলেন। আইনস্টাইন বিশ্বাস করতেন যে, ইলেক্ট্রন এবং প্রোটনের আধানের মধ্যে হয়তো অসাম্য থাকতে পারে যার ফলে পৃথিবীর চৌম্বকীয় ক্ষেত্রটি পুরো পৃথিবী দ্বারাই উৎপন্ন হয়। নোবেল পুরস্কার বিজয়ী প্যাট্রিক ব্ল্যাকেট কৌণিক ভরবেগ এবং চৌম্বকীয় ভরবেগের মধ্যে মৌলিক সম্পর্কের সন্ধানে একাধিক পরীক্ষা-নিরীক্ষা করেছিলেন, কিন্তু তিনি কিছুই খুঁজে পাননি।^[৪]^[৫]

ওয়াল্টার এম এলসাসার, বর্তমানে গৃহীত ডায়নামো তত্ত্বের একজন "পিতা" হিসাবে বিবেচিত হয়েছিলেন, পৃথিবীর চৌম্বকত্বের গ্রহণযোগ্য ব্যাখ্যা করার জন্য। তিনি প্রস্তাব করেছিলেন, এই চৌম্বকক্ষেত্রটি পৃথিবীর তরল বহিরাংশে তড়িৎপ্রবাহের ফলে তৈরি হয়েছে। তিনি পাথরের খনিজগুলির চৌম্বকীয় বিশ্লেষণ করে পৃথিবীর চৌম্বকক্ষেত্রের ইতিহাস প্রকাশ করেছিলেন।

ওহমিক ক্ষয়ের (যা ২০,০০০ বছরের মধ্যে দ্বিমেরুক্ষেত্রের জন্য ঘটে) বিরুদ্ধে চৌম্বকীয় ক্ষেত্রটি বজায় রাখতে, পৃথিবীর বাহ্যিক কোরটি অবশ্যই পরিচলনরত হতে হবে। এই পরিচিলনটি তাপীয় পরিচলন এবং ভূপৃষ্ঠের পদার্থের পরিচলন দোনোভাবেই হয়ে থাকে। আবরনটি কোর থেকে তাপ নিষ্কাশনের হার নিয়ন্ত্রণ করে। এই তাপের উৎসগুলো হলো, পৃথিবীর কোরের সংকোচনের ফলে যে মহাকর্ষীয় শক্তির নিঃস্বরন হয়, ক্রমবর্ধমান পৃথিবীর অভ্যান্তরীন কোরে আলোক নিঃস্বরনকারী উপাদানগুলি (যেমন সালফার, অক্সিজেন বা সিলিকন) কে প্রত্যাখ্যান করতে যে মহাকর্ষীয় শক্তির নিঃস্বরন হয়, অভ্যন্তরীণ কোরের স্ফটিকগুলোর সুপ্ত তাপ, এবং পটাশিয়াম, ইউরেনিয়াম এবং থোরিয়ামের তেজস্ক্রিয়তা।^[৬]

একবিংশ শতাব্দীর প্রথম দিকে, পৃথিবীর চৌম্বকক্ষেত্রের গাণিতিক মডেল সফলভাবে দেখানো যায়নি, যদিও হয়তো তা ছিল বলে মনে করা হয়। প্রাথমিক মডেলগুলি গ্রহের তরল বাহ্যিক কোরের মধ্যে পরিচলন দ্বারা চৌম্বকক্ষেত্র তৈরির উপর দৃষ্টিপাত করেছিলো। পৃথিবীর মতো শক্তিশালী চৌম্বক ক্ষেত্রের মতো গ্রহগুলোর চৌম্বকক্ষেত্রের উৎস ব্যাখ্যা করা সম্ভব ছিলো যখন মডেলটিতে অভিন্ন কোর-পৃষ্ঠের তাপমাত্রা এবং কোরের তরলের ব্যতিক্রমী রকম উচ্চ সান্দ্রতা থাকে। হিসেবগুলো খুবই বাস্তব সম্মত ফলাফল দিচ্ছিলো, এমনকি যে গ্রহগুলো পৃথিবীর সাথে কম মিলে এমন চৌম্বকক্ষেত্রের ব্যাপারেও গণনাগুলো এমন ফলাফল দিচ্ছিলো, যাতে করে হিসেবের কোথায় ভুল তা উপলব্ধি করে তা সংশোধন করে নেয়া যায়। কোর-পৃষ্ঠের তাপমাত্রায় কয়েক মিলি কেলভিনের সামান্য কিছু পরিবর্তনও পরিচলন প্রবাহ অনেক বাড়িয়ে দেয় যা চৌম্বকক্ষেত্রের আরো বাস্তব ব্যাখ্যা দিতে পারে। ^[৭]^[৮]

প্রচলিত সংজ্ঞা[সম্পাদনা]

ডায়নামো তত্ত্ব সেই প্রক্রিয়াটির বর্ণনা দেয় যার মাধ্যমে একটি ঘূর্ণনশীল, পরিচলনরত এবং তড়িৎপরিবাহী তরল পদার্থ চৌম্বকীয় ক্ষেত্র বজায় রাখে। এই তত্ত্বটি জ্যোতিঃপদার্থবিদ্যায় বিভ্রান্তিকর দীর্ঘমেয়াদী চৌম্বকীয় ক্ষেত্রগুলির উপস্থিতি ব্যাখ্যা করতে ব্যবহৃত হয়। ভূ-ডায়নামোতে পরিবাহী তরল হিসেবে বাহ্যিক কোরে তরল আয়রন এবং সৌর ডায়নামোতে ট্যাচোক্লাইন (tachocline) এ আয়নীকৃত গ্যাস রয়েছে। জ্যোতিঃপদার্থবিদ্যায় ডায়নামো তত্ত্ব দ্বারা তরলটি কীভাবে ক্রমাগত চৌম্বকক্ষেত্রকে পুনরূৎপাদন করে তা বের করতে চৌম্বকীয় হাইড্রোডাইনামিক (magnetohydrodynamic) সমীকরণ ব্যবহার করা হয়।^[৯]

একসময় বিশ্বাস করা হত যে দ্বিমেরু, যা পৃথিবীর চৌম্বকক্ষেত্রের বেশিরভাগ অংশ নিয়ে গঠিত এবং 11.3 ডিগ্রি দ্বারা আবর্তনের অক্ষ বরাবর বিভাজিত হয়, এটি পৃথিবীতে পদার্থগুলির স্থায়ী চৌম্বকত্বের কারণে হয়েছিল। এর অর্থ হল ডায়নামো তত্ত্ব দ্বারা সূর্যের চৌম্বকীয় ক্ষেত্র ব্যাখ্যা করা হয়েছিল, পৃথিবীর সাথে তার সম্পর্ক বিবেচনা করে। যাইহোক, ১৯৯১ সালে জোসেফ লারমোর দ্বারা প্রাথমিকভাবে প্রস্তাবিত এই প্রস্তাবনাটি চৌম্বক নিরপেক্ষ বৈচিত্র (secular variation), প্যালিওম্যাগনেটিজম paleomagnetism (মেরু পরিবর্তন সহ), ভূমিকম্প এবং সৌরজগতের উপাদানগুলির ব্যাপারে ব্যাপক অধ্যয়নের কারণে সংশোধিত হয়েছে। এছাড়াও, কার্ল ফ্রেডরিখ গাউসের তত্ত্বগুলি চৌম্বকীয় পর্যবেক্ষণে প্রয়োগ করে প্রমাণিত হয়েছিল যে পৃথিবীর চৌম্বকীয় ক্ষেত্রর উৎসটি বাহ্যিক এর পরিবর্তে অভ্যন্তরীণ ছিল।

ডায়নামো পরিচালনা করার জন্য তিনটি প্রয়োজনীয়তা রয়েছে:

একটি তড়িৎ পরিবাহী তরল মাধ্যম
আবর্তনশীল ঘূর্ণনের ফলে উৎপন্ন গতিশক্তি
তরলের মধ্য দিয়ে পরিচলন গতি চালানোর জন্য একটি অভ্যন্তরীণ শক্তির উৎস।^[১০]

পৃথিবীর ক্ষেত্রে চৌম্বকক্ষেত্রটি বাহ্যিক কোরে তরল আয়রনের পরিচলন দ্বারা উৎপন্ন হয় ও বজায় থাকে। চুম্বকক্ষেত্রের আবেশের জন্য কোন ঘূর্ণয়মান তরল প্রয়োজন। কোরিওলিস প্রভাব বাইরের কোরে এই ঘূর্ণন দেয় যা পৃথিবীর আবর্তনের ফলে উৎপন্ন হয়। কোরিওলিস বল ঘূর্ণন অক্ষের সাথে তরল গতি এবং তড়িৎ প্রবাহকে পর্যায় (টেইলর পর্যায়ও দেখুন) অনুসারে সংগঠিত করে। আবেশ বা চুম্বকক্ষেত্র তৈরি আবেশ সমতা (induction equation) দ্বারা ব্যাখ্যা করা যায়ঃ

{\frac {\partial \mathbf {B} }{\partial t}}=\eta \nabla ^{2}\mathbf {B} +\nabla \times (\mathbf {u} \times \mathbf {B} )

এখানে u হলো গতি, B হলো চুম্বকক্ষেত্র, t হলো সময়, এবং $\eta =1/(\sigma \mu )$ হলো চৌম্বক বিকীরক (magnetic diffusivity) যখন $\sigma$ হলো তড়িৎ পরিবাহিতা এবং $\mu$ হলো ভেদনযোগ্যতা(permeability). সমীকরনের ডান পাশে শেষ অংশের সাথে প্রথম অংশের ভাগফলকে চৌম্বক রেনল্ড রাশি বলে, যা বিকীরনের প্রতি চুম্বকক্ষেত্রের একটি দিক বিহীন রাশি।

তাপীয় স্রোতের ডায়নামো সমর্থন[সম্পাদনা]

প্রদক্ষিণকারী অপার্থিব বস্তুগুলোর মাঝে স্রোত এক প্রকার ঘর্ষণ সৃষ্টি করে যা তাদের অভ্যন্তরীণ অংশকে উত্তপ্ত করে। একে তাপীয় স্রোত বলে, এটি অভ্যন্তরটিকে তরল অবস্থায় রাখতে সহায়তা করে। ডায়নামো উৎপন্ন করতে একটি তরল অভ্যন্তর প্রয়োজন যা তড়িৎপরিবহন করতে পারে। শনির এনস্ল্যাডাস এবং বৃহস্পতির আইওগুলির অভ্যন্তরীণ কোরকে তরল রাখতে যথেষ্ট তাপীয় স্রোত রয়েছে, তবে তারা কোনও ডায়নামো তৈরি করতে পারে না কারণ তারা বিদ্যুৎ পরিবহন করতে পারে না।^[১১]^[১২] বুধের ছোট আকার থাকা সত্ত্বেও একটি চৌম্বকীয় ক্ষেত্র রয়েছে, কারণ এতে লৌহ মিশ্রিত পরিবাহী তরল কোর রয়েছে এবং এর ঘর্ষণ একটি শক্তিশালী উপবৃত্তাকার কক্ষপথ তৈরি করে।^[১৩] পৃথিবীর সাথে স্বল্প-স্থায়ী দূরত্বে অবস্থানের কারণে উৎপন্ন তাপীয় স্রোত এবং চৌম্বকীয় চন্দ্র শিলা থেকে প্রাপ্ত প্রমাণের ভিত্তিতে তাত্ত্বীয় ভাবে দেখা যায় যে চাঁদের একসময় চৌম্বকীয় ক্ষেত্র ছিল।^[১৪] কোন গ্রহের কক্ষপথ এবং ঘূর্ণন একটি তরল কোর উৎপন্ন করতে সহায়তা করে এবং গতিশক্তি সরবরাহ করে যা ডায়নামো ক্রিয়াকে সমর্থন করে।

ডায়নামো তত্ত্ব গতিবিদ্যা[সম্পাদনা]

ডায়নামো তত্ত্ব গতিবিদ্যায় গতিশীল চলকের পরিবর্তে এর গতিবেগের ক্ষেত্র নির্ধারন করা হয়। এই পদ্ধতিটি সম্পূর্ণ অরৈখিক বিশৃঙ্খল ডায়নামোর সময়ের সাথে পরিবর্তনশীল আচরণ দেখাতে পারে না তবে চৌম্বকীয় ক্ষেত্রের শক্তিমত্তা কীভাবে তার প্রবাহের কাঠামো এবং গতির সাথে পরিবর্তিত হয় তা বুঝতে সহায়তা করে।

ম্যাক্সওয়েলের সমীকরণ ব্যবহার করে একইসাথে ওহমের সূত্রকে কার্ল করে যদি চৌম্বকীয় ক্ষেত্রটি বেগের ক্ষেত্র থেকে স্বাধীন বলে ধরে নেই, তবে চৌম্বকীয় ক্ষেত্র (B) এর জন্য রৈখিক আইগেনভ্যালু সমীকরণ বের করা যায়। এর মাধ্যমে একটি জটিল চৌম্বকীয় রেনল্ড রাশি পাওয়া যায়, যার উপরে মান হলে চৌম্বকক্ষেত্রটি বিকশিত হতে পারে এবং যার নিচে মান হলে তা ক্ষয় হয়ে যায়।

ডায়নামো তত্ত্ব গতিবিদ্যার সবচেয়ে কার্যকর বৈশিষ্ট্য হলো, এটি একটি বেগ ক্ষেত্র কিনা, ডায়নামো ক্রিয়ায় সক্ষম কিনা তা পরীক্ষা করতে ব্যবহার করা যেতে পারে। একটি ছোট চৌম্বকীয় ক্ষেত্রে একটি নির্দিষ্ট বেগের ক্ষেত্র প্রয়োগ করা হলে প্রয়োগকৃত বেগের সাপেক্ষে চৌম্বকক্ষেত্রটি বৃদ্ধি পায় কিনা তা পর্যবেক্ষণ করে দেখা যায়। যদি চৌম্বকীয় ক্ষেত্রটি বৃদ্ধি পায় তবে সিস্টেমটি হয় ডায়নামো, অথবা ডায়নামো ক্রিয়ায় সক্ষম। আর যদি চৌম্বকক্ষেত্রটি বৃদ্ধি না পায় তবে কেবল এটা বোঝা যায় যে, এটি ডায়নামো নয়।

ঝিল্লি দৃষ্টান্ত(membrane paradigm) হলো কৃষ্ণগহ্বরের দিকে তাকানোর একটি উপায় যা তাদের পৃষ্ঠতলের কাছে থাকা পদার্থগুলিকে ডায়নামো তত্ত্বের ভাষায় প্রকাশ করতে দেয়।

ভূ-সম্পূর্ণপ্রতিসাম্যের(supersymmetry) স্বতঃস্ফূর্ত ভাঙ্গন[সম্পাদনা]

ডায়নামো তত্ত্ব গতিবিদ্যাকে ব্যাকগ্রাউন্ড পদার্থগুলোর প্রবাহের সাথে সম্পর্কিত সম্ভব্যতার ডিফারেনশিয়াল সমীকরণের ভূ-সম্পূর্ণপ্রতিসাম্যের স্বতঃস্ফূর্ত ভাঙ্গনের ঘটনা হিসাবেও দেখা যেতে পারে।^[১৫] সম্ভব্যতার সম্পূর্ণপ্রতিসাম্য তত্ত্বের (supersymmetric theory of stochastics) অনুযায়ী, সম্পূর্ণপ্রতিসাম্য হলো সকল সম্ভব্যতার ডিফারেনশিয়াল সমীকরণের একটি অভ্যন্তরীণ বৈশিষ্ট, যার অর্থ হলো সময়ের সাথে চলমান প্রবাহ দ্বারা মডেলের দশাগুলোর অবস্থানের ধারাবাহিকতা রক্ষা করা এবং এর স্বতঃস্ফূর্ত ভাঙ্গন হলো বিশৃঙ্খল নির্ণায়ক(deterministic chaos) ধারণার সম্ভব্যতার সাধারণ প্রকাশ।^[১৬] অন্য কথায়, ডায়নামো গতিবিদ্যা হলো ব্যাকগ্রাউন্ড পদার্থগুলোর অন্তর্নিহিত প্রবাহের বিশৃঙ্খলার প্রকাশ।

অরৈখিক ডায়নামো তত্ত্ব[সম্পাদনা]

গতিবিদ্যায় আসন্ন মানগুলো অকার্যকর হয়ে যায়, যখন চৌম্বক ক্ষেত্র তরল গতিকে প্রভাবিত করার মতো যথেষ্ট শক্তিশালী হয়ে উঠে। সেক্ষেত্রে বেগের ক্ষেত্রটি লরেন্জ বল দ্বারা প্রভাবিত হয় অতএব আবেশের সমীকরণটি চৌম্বকীয় ক্ষেত্রে আর রৈখিক হয় না। এর ফলে বেশিরভাগ ক্ষেত্রেই ডায়নামোটির বিস্তার হ্রাস পায়। এই জাতীয় ডায়নামোগুলকে অন্বক সময় হাইড্রোম্যাগনেটিক বা জলচৌম্বকীয় ডায়নামো ও বলা হয়।^[১৭] কার্যতঃ জ্যোতিঃপদার্থবিদ্যা এবং ভূ-পদার্থবিদ্যার সকল ডায়নামোই হাইড্রোম্যাগনেটিক ডায়নামো।

এই তত্ত্বের প্রধান ধারণা হলো, কোন কিছুর বহিরাবরণীতে যত ছোট চৌম্বকীয় ক্ষেত্রই থাকুক না কেন, তা লরেঞ্জ বলের প্রভাবে চলমান তরলে এক প্রকার তড়িৎপ্রবাহ তৈরি করে। এম্পিয়ারের সূত্রানুযায়ী এই প্রবাহটি আবার একটি চৌম্বক ক্ষেত্র তৈরি করে। তরল গতির কারণে এই প্রবাহ এমনভাবে বাহিত হয়, যাতে চৌম্বক ক্ষেত্র শক্তিশালী হয়ে ওঠে (যতক্ষন পর্যন্ত $\mathbf {u} \cdot (\mathbf {J} \times \mathbf {B} )$ ঋণাত্মক থাকে^[১৮])। এভাবেই একটি চৌম্বক ক্ষেত্রের "বীজ" বড় হতে থাকে, যতক্ষণ পর্যন্ত তা অচৌম্বকীয় বলের সমান হয়।

সম্পূর্ণ অরৈখিক ডায়নামোগুলো সিমুলেশন করতে সংখ্যাসূচক মডেল ব্যবহার করা হয়। নিম্নলিখিত সমীকরণগুলি ব্যবহৃত হয়ঃ

আবেশন সমীকরণ, যা উপরে উল্লেখ করা হয়েছে।
নগণ্য তড়িৎক্ষেত্রের জন্য ম্যাক্সওয়েলের সমীকরণঃ

\nabla \cdot \mathbf {B} =0

\nabla \times \mathbf {B} =\mu _{0}\mathbf {J}

ভরের নিত্যতার জন্য চলমান সমীকরণ, যার জন্য বোসিনেস্কীয় আসন্ন মান(Boussinesq approximation) ব্যবহৃত হয়ঃ

\nabla \cdot \mathbf {u} =0,

ভরবেগের নিত্যতার জন্য নেভিয়ার-স্টোকস সমীকরন, বাহ্যিক বল হিসেবে চৌম্বকীয় বল এবং মহাকর্ষীয় বলের জন্য একই আসন্ন মানটি হবেঃ

{\frac {D\mathbf {u} }{Dt}}=-{\frac {1}{\rho _{0}}}\nabla p+\nu \nabla ^{2}\mathbf {u} +\rho '\mathbf {g} +2\mathbf {\Omega } \times \mathbf {u} +\mathbf {\Omega } \times \mathbf {\Omega } \times \mathbf {R} +{\frac {1}{\rho _{0}}}\mathbf {J} \times \mathbf {B} ,

এখানে

\nu

হলো গতীয় সান্দ্রতা,

\rho _{0}

হলো লঘিষ্ট ঘণত্ব, এবং

\rho '

হলো প্লবতা প্রবণতার আপেক্ষিক ঘণত্ব (তাপীয় পরিচলনের ক্ষেত্রে

\rho '=\alpha \Delta T

যেখানে

\alpha

হলো তাপীয় প্রসারণ সহগ),

\Omega

হলো পৃথিবীর ঘূর্ণনের হার এবং

\mathbf {J}

হলো তড়িৎপ্রবাহ ঘণত্ব।

একটি সাধারণ তাপীয়(অনেক সময় আলোক কণারও) পরিবহন সমীকরণঃ

{\frac {\partial T}{\partial t}}=\kappa \nabla ^{2}T+\epsilon

এখানে T হলো তাপমাত্রা,

\kappa =k/\rho c_{p}

হলো তাপীয় বিকীরন যেখেন k হলো তাপ পরিবাহীতা,

c_{p}

হল তাপ ধারকত্ব,

\rho

হলো ঘণত্ব এবং

\epsilon

হলো অতিরিক্ত তাপ উৎস। অনেক সময় এই চাপটি কেন্দ্রাভীমুখিতা-মুক্ত জলীয় গতিশীল চাপ হইয়ে থাকে।

এই সমীকরনগুলো দিকমুখীতা মুক্ত হয়, যা দিকমুখীতা মুক্ত সহগ উৎপন্ন করে।

Ra={\frac {g\alpha TD^{3}}{\nu \kappa }},E={\frac {\nu }{\Omega D^{2}}},Pr={\frac {\nu }{\kappa }},Pm={\frac {\nu }{\eta }}

এখানে Ra হলো রেলেই(Rayleigh) সংখ্যা, E হলো একম্যান(Ekman) সংখ্যা, Pr এবং Pm হলো যথাক্রমে প্র্যান্ডটেল(Prandtl) এবং চৌম্বকীয় প্র্যান্ডটেল(magnetic Prandtl) সংখ্যা। চৌম্বকীয় ক্ষেত্র স্কেল অনেক সময় এলসাসার(Elsasser) সংখ্যা এককে হয়, $B=(\rho \Omega /\sigma )^{1/2}$ .

চৌম্বক এবং গতি শক্তির রুপান্তর[সম্পাদনা]

উপরের নেভিয়ার-স্টোকস সমীকরণের সাথে $\rho _{0}\mathbf {u}$ এর স্কেলার গুণন করলে সমীকরনের বামপাশে গতিশক্তির ঘণত্বের বৃদ্ধিহার, $(1/2)\rho _{0}u^{2}$ পাওয়া যায়। আর ডান পাশে অবশিষ্ট অংশটি হলো, $\mathbf {u} \cdot (\mathbf {J} \times \mathbf {B} )$ , লরেঞ্জ(Lorentz) বলের ফলে গতিশক্তির প্রভাব।

আবেশন সমীকরণের সাথে $(1/\mu _{0})\mathbf {B}$ এর স্কেলার গুণনের ফলে সমীকরনের বাম পাশে চৌম্বকীয় শক্তির ঘণত্বের বৃদ্ধিহার $(1/2\mu _{0})B^{2}$ পাওয়া যায়। আর ডান পাশে অবশিষ্ট অংশটি হলো, $(1/\mu _{0})\mathbf {B} \cdot \left(\nabla \times (\mathbf {u} \times \mathbf {B} )\right)$ . যেহেতু সমীকরণটি আয়তনের ইন্টিগ্রেশন করা, তাই এটি সীমানার(boundary) সমতুল্য (এবং স্কেলার তৃতীয় গুণন stp দুইবার করা হলে) $-\mathbf {u} \cdot \left((1/\mu _{0})(\nabla \times \mathbf {B} )\times \mathbf {B} )\right)=-\mathbf {u} \cdot (\mathbf {J} \times \mathbf {B} )$ (যেখানে ম্যাক্সওয়েলের একটি সমীকরণ ব্যবহৃত হয়েছে). এটি হলো তরল গতির ফলে চৌম্বকীয় শক্তির স্থানীয় প্রভাব।

সুতরাং $-\mathbf {u} \cdot (\mathbf {J} \times \mathbf {B} )$ এটি হলো গতিশক্তি থেকে চৌম্বক শক্তির রুপান্তরের হার। কাজেই এর মান ঋণাত্মক হওয়া চলবে না, অন্তত ডায়নামো থেকে চৌম্বক ক্ষেত্র তৈরির আয়তনটি।^[১৮]

পৃথিবীর ডায়নামো দ্বারা তৈরি চৌম্বক ক্ষেত্রের বিস্তারের মাত্রা[সম্পাদনা]

উপরোল্লোখিত গতিশক্তি থেকে চৌম্বক শক্তির রুপান্তর হারের সমীকরণটি $\mathbf {u}$ গতি সম্পন্ন বহিরাবরণীর বল $\mathbf {J} \times \mathbf {B}$ এর দ্বারা কৃত কাজের সমতুল্য। এই কাজটি হলো প্রকৃতপক্ষে তরলের উপর অচৌম্বকীয় বলের ফল।

অবশ্যই মহাকর্ষীয় বল এবং কেন্দ্রাতীগ বল দুটি সংরক্ষণশীল, ফলে আবদ্ধ আবর্তনের ক্ষেত্রে চলমান তরলের ওপর সামগ্রীকভাবে এদের কোন প্রভাব নেই। একম্যান সংখ্যা(উপরে উল্লেখিত) এটি হলো অবশিষ্ট দুটি বল সান্দ্রতা এবং করিওলিস বলের ভগ্নাংশ যা পৃথিবীর বহিরাংশে অত্যন্ত দূর্বল, কারণ তরলের কারণে এর সান্দ্রতা খুবই কম (1.2-1.5 x10⁻² প্যাস্কেল সেকেন্ড ps ^[১৯])

সুতরাং গড় সময়ে কেবল করিওলিস বলটি ক্রিয়াশীল থাকে, যার মান হলো $-2\rho \,\mathbf {\Omega } \times \mathbf {u}$ , এটি এবং $\mathbf {J} \times \mathbf {B}$ বল সাধারণভাবে নয়, কেবল মাত্র পরোক্ষভাবে সম্পর্কযুক্ত(অর্থাৎ তারা একে অপরের উপর ক্রিয়া করে তবে একই সময়ে একই যায়গায় নয়)।

ওহমের সূত্রানুসারে প্রবাহ ঘণত্ব J নিজেই হলো চৌম্বকক্ষেত্রের ফল। আবার পদার্থের গতি এবং তড়িৎপ্রবাহের ফলে ক্ষেত্রটি একই সময় এবং যায়গায় হওয়া জরুরী নয়। যাইহোক, এই সম্পর্কগুলো প্রশ্ন অনুসারে বিস্তার অনুমান করতে ব্যবহার করা যেতে পারে।

বিস্তারের বিন্যাসের ক্ষেত্রে $J\,B\sim \rho \,\Omega \,u$ এবং $J\sim \sigma uB$ , থেকে পাই $\sigma \,u\,B^{2}\sim \rho \,\Omega \,u$ , অথবাঃ

B\sim {\sqrt {\frac {\rho \,\Omega }{\sigma }}}

সমীকরনের দু'পাশের ভগ্নাংশ হলো এলসাসার সংখ্যার বর্গমূল।

লক্ষনীয়, আসন্ন মান থেকে চৌম্বক ক্ষেত্রের দিক অনুমান করা যায় না(অন্ততপক্ষে চিহ্ন) যেহেতু এটা বর্গকৃত এবং অনেক সময়, বিপরীতকরন কৃত, যদিও সাধারণত এটি $\mathbf {\Omega }$ এর সাথে একই অক্ষে ফেরান থাকে।

পৃথিবীর বহিরাবরণীর ক্ষেত্রে, ρ এর আসন্ন মান 10⁴ kg/m³,^[১৯] Ω=2π/day = 7.3x10⁻⁵ সেকেন্ড এবং σ এর আসন্ন মান 10⁷Ω⁻¹m⁻¹.^[২০] যার ফল 2.7x10⁻⁴ টেসলা (T).

চৌম্বক ক্ষেত্রের চৌম্বক দ্বিমেরুর দূরত্বের ক্ষেত্রে একপ্রকার ঘণকীয় সম্পর্ক রয়েছে, তাই ভূপৃষ্ঠের বিস্তারের বিন্যাস এর আসন্ন মান পাওয়া যাবে উপরের মানের সাথে (R_{outer core}/R_Earth)³ = (2890/6370)³ = 0.093, গুণ করে, যার ফল 2.5x10⁻⁵ টেসলা, যা ইকুয়েটরে(equator) প্রাপ্ত মান 3x10⁻⁵ টেসলার কাছাকাছি।

সংখ্যাতাত্ত্বিক মডেলগুলো[সম্পাদনা]

ব্যাপকভাবে বললে, ভূ-ডায়নামোর মডেলগুলি উপরের অনুচ্ছেদগুলিতে উল্লিখিত কিছু শর্ত এবং সমীকরণে পর্যবেক্ষণকৃত তথ্যের সাথে সামঞ্জস্য রেখে চৌম্বকীয় ক্ষেত্র তৈরির চেষ্টা করে। এক্ষেত্রে জলচৌম্বকগতির (magnetohydrodynamic) সমীকরণগুলি সফলভাবে বাস্তবায়নের বিশেষ গুরুত্ব রয়েছে, কারণ তারা ডায়নামোর মডেলগুলিকে স্ব-সামঞ্জস্যতার দিকে নিয়ে যায়। যদিও ভূ-ডায়নামো মডেলগুলি বহুল প্রচলিত, এবং ডায়নামো মডেলগুলি কেবল ভূ-ডায়নামোতেই সীমাবদ্ধ নয়; সৌর এবং সাধারণ ডায়নামো মডেলগুলিতেও এগুলির অংশ রয়েছে। ভূতত্ত্ববিদ্যায় ডায়নামো মডেলগুলি বিশ্লেষনের বেশ উপযোগিতা রয়েছে কারণ এর মাধ্যমে পৃথিবীর মতো জ্যোতিঃপদার্থবিদ্যার জিনিসগুলো কীভাবে চৌম্বকীয় ক্ষেত্র গঠন করে এবং কীভাবে চৌম্বকীয় ক্ষেত্রগুলিতে মেরু বিপরীতকরনের মতো কিছু বৈশিষ্ট্য প্রদর্শন করে তা বোঝা যায়।

ডায়নামোর সংখ্যাতাত্ত্বিক মডেলগুলিতে ব্যবহৃত সমীকরণগুলি অত্যন্ত জটিল। কয়েক দশক ধরে, তাত্ত্বিকরা উপরে বর্ণিত দ্বিমাত্রিক গতিশীল ডায়নামো মডেলের মধ্যে সীমাবদ্ধ ছিলেন, যেখানে আগেই তরল গতি বেছে নিয়ে চৌম্বকীয় ক্ষেত্রের প্রভাব নির্ণয় করা হয়েছিল। ডায়নামোর ত্রিমাত্রিক মডেলগুলিতে জলচৌম্বকীয়গতির সমীকরণগুলি সমাধানের ক্ষেত্রে মূলত বাধা ছিলো- গতিশীল মডেলগুলিতে অনেকগুলি অনুমানের প্রয়োজন হয়েছিল,রৈখিক থেকে অরৈখিক পর্যন্ত অগ্রগতি এই বাধা দূর করে এবং মডেলগুলিতে স্ব-সামঞ্জস্যতার সুযোগ দেয়।

১৯৯৫ সালে বিজ্ঞানীদের দুটি দল প্রথম স্ব-সামঞ্জস্যপূর্ণ ডায়নামো মডেল যা তরল গতি এবং চৌম্বকীয় ক্ষেত্র উভয়ই নির্ধারণ করে, উদ্ভাবন করেন, যার একটি জাপানে^[২১] এবং অপরটি মার্কিন যুক্তরাষ্ট্রে^[২২]^[২৩]। পরবর্তী মডেলটি ভূ-ডায়নামো হিসেবে তৈরি হয়েছিল এবং তা উল্লেখযোগ্য সাড়া ফেলেছিল কারণ তা পৃথিবীর চৌম্বকক্ষেত্রের কয়েকটি বৈশিষ্ট্য সফলভাবে পুনরুৎপাদন করে দেখিয়েছিল।^[১৮] এই যুগান্তকারী মডেলটি অনুসরণ করার পরে যুক্তিসঙ্গত ত্রিমাত্রিক ডায়নামো মডেলের বিকাশ ঘটে।^[১৮]

যদিও এখন অনেক স্ব-সামঞ্জস্যপূর্ণ মডেল রয়েছে, তবে তারা যে ফলাফলগুলি দিচ্ছে এবং যেভাবে বিকশিত হয়েছে, তার মাঝে অনেক পার্থক্য রয়েছে।^[১৮] ভূ-ডায়নামো মডেল উদ্ভাবনের ক্ষেত্রে জটিলতা রয়েছে, অনেক ক্ষেত্রেই সমস্যা তৈরি হতে পারে যেমন, ডায়নামোর শক্তি সরবরাহ প্রক্রিয়ার অনুমানগুলির সময়, সমীকরণে ব্যবহৃত প্যারামিটারগুলির মান নির্বাচনের সময়, বা সমীকরণগুলিকে স্বাভাবিক করার সময়। ঘটতে পারে এমন অনেক পার্থক্য থাকা সত্ত্বেও, বেশিরভাগ মডেলের স্পষ্ট অক্ষীয় দ্বিমেরুর মতো বৈশিষ্ট্য রয়েছে। এর মধ্যে অনেক মডেলে নিরপেক্ষ পরিবর্তন (secular variation) এবং ভূ-চৌম্বকীয় মেরু বিপরীতকরনের (geomagnetic polarity reversals) মতো ব্যাপারগুলি সফলভাবে পুনঃতৈরি হয়েছে।^[১৮]

পর্যবেক্ষণ[সম্পাদনা]

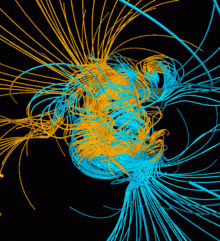
ডায়নামো মডেল থেকে অনেক রকম পর্যবেক্ষণ তৈরি করা যেতে পারে। সময়ের সাথে কীভাবে চুম্বকীয় ক্ষেত্রগুলি পরিবর্তিত হয় এবং মডেল ও পৃথিবীর মধ্যে মিল খুঁজে পেতে প্যালিওম্যাগনেটিক (paleomagnetic) ডেটার সাথে তুলনা বোঝার জন্য এই মডেলগুলি ব্যবহার করা যেতে পারে। অনেক ক্ষেত্রে প্যালিওম্যাগনেটিক পর্যবেক্ষণের অনিশ্চয়তার কারণে তুলনাগুলি সম্পূর্ণ যুক্তিযুক্ত বা কার্যকর হতে পারে না।^[১৮] সরলিকৃত ভূ-ডায়নামো মডেলগুলি ডায়নামো সংখ্যার (বাইরের কোরে ঘূর্ণন হারের পরিবর্তনশীলতা(variance in rotational rates) এবং প্রতিবিম্ব-অসমমিতিক পরিচলন দ্বারা প্রাপ্ত (যেমন যখন পরিচলনটি উত্তর দিকে থাকে, অপরটি তখন দক্ষিণে থাকে)) এবং চৌম্বকীয় মেরু বিপরীতকরনের মধ্যে সম্পর্ক দেখায়, যেমনটা ভূ-ডায়নামো এবং সূর্যের ডায়নামোর মধ্যে মিল পাওয়া যায়।^[১৮] অনেক মডেলের ক্ষেত্রে এমনটা হয় যে, চৌম্বকীয় ক্ষেত্রগুলিতে কিছু এলোমেলো দৈর্ঘ্য থাকে, যা স্বাভাবিক প্রবণতা অনুসরণ করে গড়ে যার ফলাফল শূন্য।^[১৮] এই পর্যবেক্ষণগুলি ছাড়াও, ভূ-ডায়নামোতে শক্তি সরবরাহ প্রক্রিয়া সম্পর্কে সাধারণ পর্যবেক্ষণগুলি পৃথিবী থেকে সংগৃহীত প্রকৃত উপাত্তকে কতটা সঠিকভাবে প্রতিফলিত করে তার উপর ভিত্তি করে তৈরি করা যেতে পারে।

আধুনিক মডেলিং[সম্পাদনা]

ডায়নামো মডেলিংয়ের জটিলতা এত বেশি যে, ভূ-ডায়নামোর মডেলগুলি সুপার কম্পিউটারের বর্তমান শক্তি পর্যন্ত সীমাবদ্ধ, কারণ বিশেষত বাইরের কোরের একম্যান এবং রেলেই সংখ্যা নির্ণয় করা অত্যন্ত কঠিন এবং এর জন্য বিপুল সংখ্যক হিসেব গণনার প্রয়োজন।

১৯৯৫ সালে স্ব-সামঞ্জস্যপূর্ণ যুগান্তকারী মডেলটি হওয়ার পর থেকে ডায়নামো মডেলিংয়ে অনেক উন্নত প্রস্তাবনা হয়েছে। জটিল চৌম্বকীয় ক্ষেত্রের পরিবর্তনগুলি বিশ্লেষণ করার একটি পরামর্শ হলো গণনা সহজ করার জন্য বর্ণালী পদ্ধতি(spectral methods) প্রয়োগ করা।^[২৪] শেষ পর্যন্ত কম্পিউটার পাওয়ারে যথেষ্ট উন্নতি না হওয়া অবধি বাস্তব সম্মত ডায়নামো মডেলগুলি গণনার পদ্ধতি আরও কর্মক্ষম করে তুলতে হবে, সুতরাং সংখ্যাতাত্ত্বিক ডায়নামো মডেলিংয়ের অগ্রগতির জন্য মডেলটির কম্পিউটিংয়ের পদ্ধতিগুলিতে উন্নতি করা অত্যন্ত গুরুত্বপূর্ণ।

আরও দেখুন[সম্পাদনা]

তথ্যসূত্র[সম্পাদনা]

↑ "How does the Earth's core generate a magnetic field?"। USGS FAQs। United States Geological Survey। ১৮ জানুয়ারি ২০১৫ তারিখে মূল থেকে আর্কাইভ করা। সংগ্রহের তারিখ ২১ অক্টোবর ২০১৩।
↑ Larmor, J. (১৯১৯)। "How could a rotating body such as the Sun become a magnet?"। Reports of the British Association। 87: 159–160।
↑ Larmor, J. (১৯১৯)। "Possible rotational origin of magnetic fields of sun and earth"। Electrical Review। 85: 412ff। Reprinted in Engineering, vol. 108, pages 461ff (3 October 1919).
↑ Nye, Mary Jo (১ মার্চ ১৯৯৯)। "Temptations of theory, strategies of evidence: P. M. S. Blackett and the earth's magnetism, 1947–52"। The British Journal for the History of Science। 32 (1): 69–92। ডিওআই:10.1017/S0007087498003495।
↑ Merrill, McElhinny এবং McFadden 1996, page 17 claim that in 1905, shortly after composing his special relativity paper, Albert Einstein described the origin of the Earth's magnetic field as being one of the great unsolved problems facing modern physicists. However, they do not provide details on where he made this statement.
↑ Sanders, Robert (২০০৩-১২-১০)। "Radioactive potassium may be major heat source in Earth's core"। UC Berkeley News। সংগ্রহের তারিখ ২০০৭-০২-২৮।
↑ Sakuraba, Ataru; Paul H. Roberts (৪ অক্টোবর ২০০৯)। "Generation of a strong magnetic field using uniform heat flux at the surface of the core"। Nature Geoscience। 2 (11): 802–805। ডিওআই:10.1038/ngeo643। বিবকোড:2009NatGe...2..802S।
↑ Buffett, Bruce (২০০৯)। "Geodynamo: A matter of boundaries"। Nature Geoscience। 2 (11): 741–742। ডিওআই:10.1038/ngeo673। বিবকোড:2009NatGe...2..741B।
↑ Brandenburg, Axel (২০০৭)। "Hydromagnetic dynamo theory"। Scholarpedia। সংগ্রহের তারিখ অক্টোবর ৭, ২০১৬।
↑ E. Pallé (২০১০)। The Earth as a Distant Planet: A Rosetta Stone for the Search of Earth-Like Worlds (Astronomy and Astrophysics Library)। Berlin: Springer। পৃষ্ঠা 316–317। আইএসবিএন 978-1-4419-1683-9। সংগ্রহের তারিখ ১৭ জুলাই ২০১০।
↑ Steigerwald, Bill (অক্টোবর ৬, ২০১০)। "Saturn's Icy Moon May Keep Oceans Liquid with Wobble"। NASA। মার্চ ২৪, ২০১৫ তারিখে মূল থেকে আর্কাইভ করা। সংগ্রহের তারিখ আগস্ট ১৪, ২০১২।
↑ Cassis, Nikki (মার্চ ১৯, ২০১২)। "Geologic map of Jupiter's moon Io details an otherworldly volcanic surface"। Astrogeology Science Center। সংগ্রহের তারিখ আগস্ট ১৪, ২০১২। ^{[স্থায়ীভাবে অকার্যকর সংযোগ]}
↑ "Mercury's Surprising Core and Landscape Curiosities"। MESSENGER। Carnegie Institution for Science। মার্চ ২১, ২০১২। জানুয়ারি ১৮, ২০১৫ তারিখে মূল থেকে আর্কাইভ করা। সংগ্রহের তারিখ আগস্ট ১৪, ২০১২।
↑ Stevens, Tim (নভেম্বর ৯, ২০১১)। "Ancient lunar dynamo may explain magnetized moon rocks"। University of California। সংগ্রহের তারিখ আগস্ট ১৪, ২০১২।
↑ Ovchinnikov, I.V.; Ensslin, T. A. (এপ্রিল ২০১৬)। "Kinematic dynamo, supersymmetry breaking, and chaos"। Physical Review D। 93 (8): 085023। arXiv:1512.01651 । ডিওআই:10.1103/PhysRevD.93.085023। বিবকোড:2016PhRvD..93h5023O।
↑ Ovchinnikov, I.V. (মার্চ ২০১৬)। "Introduction to Supersymmetric Theory of Stochastics"। Entropy। 18 (4): 108। arXiv:1511.03393 । ডিওআই:10.3390/e18040108। বিবকোড:2016Entrp..18..108O।
↑ Parker, Eugene N. (সেপ্টেম্বর ১৯৫৫)। "Hydromagnetic Dynamo Models"। The Astrophysical Journal। 122: 293–314। ডিওআই:10.1086/146087। বিবকোড:1955ApJ...122..293P।
↑ ^ক ^খ ^গ ^ঘ ^ঙ ^চ ^ছ ^জ ^ঝ Kono, Masaru; Roberts, Paul H. (২০০২)। "Recent geodynamo simulations and observations of the geomagnetic field"। Reviews of Geophysics। 40 (4): 1–53। ডিওআই:10.1029/2000RG000102। বিবকোড:2002RvGeo..40.1013K।
↑ ^ক ^খ "de Wijs, G. A., Kresse, G., Vočadlo, L., Dobson, D., Alfe, D., Gillan, M. J., & Price, G. D. (1998). The viscosity of liquid iron at the physical conditions of the Earth's core. Nature, 392(6678), 805." (পিডিএফ)। ২০ এপ্রিল ২০১৮ তারিখে মূল (পিডিএফ) থেকে আর্কাইভ করা। সংগ্রহের তারিখ ২৮ আগস্ট ২০১৯।
↑ Ohta, K., Kuwayama, Y., Hirose, K., Shimizu, K., & Ohishi, Y. (2016). Experimental determination of the electrical resistivity of iron at Earth’s core conditions. Nature, 534(7605), 95. Link to a summary
↑ Kageyama, Akira; Sato, Tetsuya (১ জানুয়ারি ১৯৯৫)। "Computer simulation of a magnetohydrodynamic dynamo. II"। Physics of Plasmas। 2 (5): 1421–1431। ডিওআই:10.1063/1.871485। বিবকোড:1995PhPl....2.1421K।
↑ Glatzmaier, Gary A.; Roberts, Paul H. (১৯৯৫)। "A three-dimensional self-consistent computer simulation of a geomagnetic field reversal"। Nature। 377 (6546): 203–209। ডিওআই:10.1038/377203a0। বিবকোড:1995Natur.377..203G।
↑ Glatzmaier, G; Roberts, Paul H. (১৯৯৫)। "A three-dimensional convective dynamo solution with rotating and finitely conducting inner core and mantle"। Physics of the Earth and Planetary Interiors। 91 (1–3): 63–75। ডিওআই:10.1016/0031-9201(95)03049-3। বিবকোড:1995PEPI...91...63G।
↑ Avery, Margaret S.; Constable, Catherine G.; Davies, Christopher J.; Gubbins, David (২০১৯-০১-০১)। "Spectral methods for analyzing energy balances in geodynamo simulations"। Physics of the Earth and Planetary Interiors। 286: 127–137। আইএসএসএন 0031-9201। ডিওআই:10.1016/j.pepi.2018.10.002। বিবকোড:2019PEPI..286..127A।

Demorest, Paul (২১ মে ২০০১)। "Dynamo Theory and Earth's magnetic Field (term paper)" (পিডিএফ)। ২১ ফেব্রুয়ারি ২০০৭ তারিখে মূল (পিডিএফ) থেকে আর্কাইভ করা। সংগ্রহের তারিখ ১৪ অক্টোবর ২০১১।
Fitzpatrick, Richard (১৮ মে ২০০২)। "MHD Dynamo Theory"। Plasma Physics। University of Texas at Austin। সংগ্রহের তারিখ ১৪ অক্টোবর ২০১১।
Merrill, Ronald T.; McElhinny, Michael W.; McFadden, Phillip L. (১৯৯৬)। The magnetic field of the earth: Paleomagnetism, the core, and the deep mantle। Academic Press। আইএসবিএন 978-0-12-491246-5।
Stern, David P.। "Chapter 12: The dynamo process"। The Great Magnet, the Earth। সংগ্রহের তারিখ ১৪ অক্টোবর ২০১১।
Stern, David P.। "Chapter 13: Dynamo in the Earth's Core"। The Great Magnet, the Earth। সংগ্রহের তারিখ ১৪ অক্টোবর ২০১১।

[1] "How does the Earth's core generate a magnetic field?"। USGS FAQs। United States Geological Survey। ১৮ জানুয়ারি ২০১৫ তারিখে মূল থেকে আর্কাইভ করা। সংগ্রহের তারিখ ২১ অক্টোবর ২০১৩।

[Larmor1919-2] Larmor, J. (১৯১৯)। "How could a rotating body such as the Sun become a magnet?"। Reports of the British Association। 87: 159–160।

[3] Larmor, J. (১৯১৯)। "Possible rotational origin of magnetic fields of sun and earth"। Electrical Review। 85: 412ff। Reprinted in Engineering, vol. 108, pages 461ff (3 October 1919).

[4] Nye, Mary Jo (১ মার্চ ১৯৯৯)। "Temptations of theory, strategies of evidence: P. M. S. Blackett and the earth's magnetism, 1947–52"। The British Journal for the History of Science। 32 (1): 69–92। ডিওআই:10.1017/S0007087498003495।

[5] Merrill, McElhinny এবং McFadden 1996, page 17 claim that in 1905, shortly after composing his special relativity paper, Albert Einstein described the origin of the Earth's magnetic field as being one of the great unsolved problems facing modern physicists. However, they do not provide details on where he made this statement.

[6] Sanders, Robert (২০০৩-১২-১০)। "Radioactive potassium may be major heat source in Earth's core"। UC Berkeley News। সংগ্রহের তারিখ ২০০৭-০২-২৮।

[7] Sakuraba, Ataru; Paul H. Roberts (৪ অক্টোবর ২০০৯)। "Generation of a strong magnetic field using uniform heat flux at the surface of the core"। Nature Geoscience। 2 (11): 802–805। ডিওআই:10.1038/ngeo643। বিবকোড:2009NatGe...2..802S।

[8] Buffett, Bruce (২০০৯)। "Geodynamo: A matter of boundaries"। Nature Geoscience। 2 (11): 741–742। ডিওআই:10.1038/ngeo673। বিবকোড:2009NatGe...2..741B।

[hydromagnetic_dynamo-9] Brandenburg, Axel (২০০৭)। "Hydromagnetic dynamo theory"। Scholarpedia। সংগ্রহের তারিখ অক্টোবর ৭, ২০১৬।

[10] E. Pallé (২০১০)। The Earth as a Distant Planet: A Rosetta Stone for the Search of Earth-Like Worlds (Astronomy and Astrophysics Library)। Berlin: Springer। পৃষ্ঠা 316–317। আইএসবিএন 978-1-4419-1683-9। সংগ্রহের তারিখ ১৭ জুলাই ২০১০।

[Enceladus-11] Steigerwald, Bill (অক্টোবর ৬, ২০১০)। "Saturn's Icy Moon May Keep Oceans Liquid with Wobble"। NASA। মার্চ ২৪, ২০১৫ তারিখে মূল থেকে আর্কাইভ করা। সংগ্রহের তারিখ আগস্ট ১৪, ২০১২।

[Io_geologic-12] Cassis, Nikki (মার্চ ১৯, ২০১২)। "Geologic map of Jupiter's moon Io details an otherworldly volcanic surface"। Astrogeology Science Center। সংগ্রহের তারিখ আগস্ট ১৪, ২০১২। ^{[স্থায়ীভাবে অকার্যকর সংযোগ]}

[mercury_core-13] "Mercury's Surprising Core and Landscape Curiosities"। MESSENGER। Carnegie Institution for Science। মার্চ ২১, ২০১২। জানুয়ারি ১৮, ২০১৫ তারিখে মূল থেকে আর্কাইভ করা। সংগ্রহের তারিখ আগস্ট ১৪, ২০১২।

[lunar_dynamo-14] Stevens, Tim (নভেম্বর ৯, ২০১১)। "Ancient lunar dynamo may explain magnetized moon rocks"। University of California। সংগ্রহের তারিখ আগস্ট ১৪, ২০১২।

[15] Ovchinnikov, I.V.; Ensslin, T. A. (এপ্রিল ২০১৬)। "Kinematic dynamo, supersymmetry breaking, and chaos"। Physical Review D। 93 (8): 085023। arXiv:1512.01651 । ডিওআই:10.1103/PhysRevD.93.085023। বিবকোড:2016PhRvD..93h5023O।

[16] Ovchinnikov, I.V. (মার্চ ২০১৬)। "Introduction to Supersymmetric Theory of Stochastics"। Entropy। 18 (4): 108। arXiv:1511.03393 । ডিওআই:10.3390/e18040108। বিবকোড:2016Entrp..18..108O।

[17] Parker, Eugene N. (সেপ্টেম্বর ১৯৫৫)। "Hydromagnetic Dynamo Models"। The Astrophysical Journal। 122: 293–314। ডিওআই:10.1086/146087। বিবকোড:1955ApJ...122..293P।

[Kono20022-18] ক ^খ ^গ ^ঘ ^ঙ ^চ ^ছ ^জ ^ঝ Kono, Masaru; Roberts, Paul H. (২০০২)। "Recent geodynamo simulations and observations of the geomagnetic field"। Reviews of Geophysics। 40 (4): 1–53। ডিওআই:10.1029/2000RG000102। বিবকোড:2002RvGeo..40.1013K।

[Wijs1998-19] ক ^খ "de Wijs, G. A., Kresse, G., Vočadlo, L., Dobson, D., Alfe, D., Gillan, M. J., & Price, G. D. (1998). The viscosity of liquid iron at the physical conditions of the Earth's core. Nature, 392(6678), 805." (পিডিএফ)। ২০ এপ্রিল ২০১৮ তারিখে মূল (পিডিএফ) থেকে আর্কাইভ করা। সংগ্রহের তারিখ ২৮ আগস্ট ২০১৯।

[20] Ohta, K., Kuwayama, Y., Hirose, K., Shimizu, K., & Ohishi, Y. (2016). Experimental determination of the electrical resistivity of iron at Earth’s core conditions. Nature, 534(7605), 95. Link to a summary

[21] Kageyama, Akira; Sato, Tetsuya (১ জানুয়ারি ১৯৯৫)। "Computer simulation of a magnetohydrodynamic dynamo. II"। Physics of Plasmas। 2 (5): 1421–1431। ডিওআই:10.1063/1.871485। বিবকোড:1995PhPl....2.1421K।

[selfconsistent-22] Glatzmaier, Gary A.; Roberts, Paul H. (১৯৯৫)। "A three-dimensional self-consistent computer simulation of a geomagnetic field reversal"। Nature। 377 (6546): 203–209। ডিওআই:10.1038/377203a0। বিবকোড:1995Natur.377..203G।

[23] Glatzmaier, G; Roberts, Paul H. (১৯৯৫)। "A three-dimensional convective dynamo solution with rotating and finitely conducting inner core and mantle"। Physics of the Earth and Planetary Interiors। 91 (1–3): 63–75। ডিওআই:10.1016/0031-9201(95)03049-3। বিবকোড:1995PEPI...91...63G।

[24] Avery, Margaret S.; Constable, Catherine G.; Davies, Christopher J.; Gubbins, David (২০১৯-০১-০১)। "Spectral methods for analyzing energy balances in geodynamo simulations"। Physics of the Earth and Planetary Interiors। 286: 127–137। আইএসএসএন 0031-9201। ডিওআই:10.1016/j.pepi.2018.10.002। বিবকোড:2019PEPI..286..127A।

[১]

[২]

[৩]

[৪]

[৫]

[৬]

[৭]

[৮]

[৯]

[১০]

[১১]

[১২]

[১৩]

[১৪]

[১৫]

[১৬]

[১৭]

[১৮]

[১৯]

[২০]

[২১]

[২২]

[২৩]

[২৪]

দে স ভূপদার্থবিজ্ঞান
বিবরন	রূপরেখা ভূপদার্থবিজ্ঞানী
বিভাগ	ভূগণিত ভূগতিবিজ্ঞান ভূপদার্থবিজ্ঞান জরিপ ভূচৌম্বকবিদ্যা ভূপদার্থবিজ্ঞানে তরল গতি গাণিতিক ভূপদার্থবিজ্ঞান খনিজ পদার্থবিজ্ঞান পৃষ্ঠের কাছাকাছি ভূপদার্থবিজ্ঞান প্যালিওম্যাগনেটিজম ভূকম্পবিদ্যা টেক্টোনিক পদার্থবিজ্ঞান
পদার্থীয় ঘটনা	ঝাঁকুনির ঝাঁকুনি করিওলিস প্রভাব পৃথিবীর চৌম্বকীয় ক্ষেত্র ভূডায়নামো ভূতাপীয় গ্রেডিয়েন্ট পৃথিবীর মাধ্যাকর্ষণ আবরন পরিচলন সমীকরণের প্রবণতা ভূমিকম্পের তরঙ্গ জোয়ার
Category Portal Commons