চৌম্বক দ্বিমেরু

চৌম্বকীয় ক্ষেত্র: প্রাকৃতিক চৌম্বকীয় দ্বিমেরুর (উপরের বাম), চৌম্বক একমেরু এর (উপরের ডানদিকে), বৃত্তাকার লুপের (নীচে বাম) কারণে বা একটি সোলেনয়েড এ (নীচের ডানদিকে)। যখন বিন্যাস অসীম ক্ষুদ্র হয় তখন সমস্তকিছু একই ক্ষেত্র-প্রোফাইল তৈরি করে।

চৌম্বক দ্বিমেরু হ'ল তড়িৎ প্রবাহ এর একটি বন্ধ লুপের সীমা অথবা চৌম্বক ভ্রামককে স্থির রেখে এক জোড়া মেরুর উৎসের আকার কমিয়ে শূন্যে পরিণত করা। এটি বৈদ্যুতিক দ্বিমেরুর চৌম্বকীয় অ্যানালগ রূপ হলেও সাদৃশ্যটি একেবারে নিখুঁত নয়। বিশেষ করে চৌম্বকীয় একমেরু বা বৈদ্যুতিক আধান এর চৌম্বকীয় অ্যানালগটি কখনও পর্যবেক্ষণ করা হয়নি। এ ছাড়াও চৌম্বকীয় দ্বিমেরু মুহুর্তের একটি মৌলিক কোয়ান্টাম ধর্ম - মৌলিক কণার ঘূর্ণন (স্পিন) এর সাথে জড়িত।

যে কোনও চৌম্বকীয় উৎসের চারপাশে চৌম্বক ক্ষেত্র, উৎস থেকে দূরত্ব বাড়ার সাথে সাথে চৌম্বকীয় দ্বিমেরু ক্ষেত্রের মতোই ক্রমবর্ধমান হতে দেখা যায়।

চৌম্বকীয় দ্বিমেরু মুহুর্ত দ্বারা উৎপাদিত বাহ্যিক চৌম্বকীয় ক্ষেত্র

চৌম্বকীয় মুহুর্তের জন্য ইলেক্ট্রোস্ট্যাটিক অ্যানালগ: সীমাবদ্ধ দূরত্ব দ্বারা পৃথক দুটি বিপরীত আধান। প্রতিটি তীর সেই বিন্দুতে ক্ষেত্র ভেক্টরের দিককে উপস্থাপন করছে।

একটি বর্তমান লুপের চৌম্বকীয় ক্ষেত্র। বলয়টি বর্তমান লুপকে উপস্থাপন করে যা x পৃষ্ঠায় চলে যায় এবং বিন্দুতে বেরিয়ে আসে।

ধ্রুপদী পদার্থবিদ্যায় দ্বিমেরুর চৌম্বক ক্ষেত্রটি হিসাব করা হয় বর্তমান লুপের সীমা হিসাবে অথবা চৌম্বকীয় মুহুর্ত m স্থির রেখে উৎস থেকে এক জোড়া চার্জ বা আধান একটি বিন্দুতে সঙ্কুচিত হওয়া থেকে। বর্তমান লুপের জন্য এই সীমাটি ভেক্টর সম্ভাব্য এর জন্য খুব সহজেই বের করা যায়। উৎস অঞ্চলের বাইরে এই সম্ভাব্যতাটি (এসআই একক এ)

${\mathbf {A} }({\mathbf {r} })={\frac {\mu _{0}}{4\pi r^{2}}}{\frac {{\mathbf {m} }\times {\mathbf {r} }}{r}}={\frac {\mu _{0}}{4\pi }}{\frac {{\mathbf {m} }\times {\mathbf {r} }}{r^{3}}},$

৪π r^২ সহ যেখানে গোলকের পৃষ্ঠের ব্যাসার্ধ r;

এবং চৌম্বকীয় ফ্লাক্স ঘনত্ব (বি-ফিল্ডের জোর) tesla এককে হয়

$\mathbf {B} ({\mathbf {r} })=\nabla \times {\mathbf {A} }={\frac {\mu _{0}}{4\pi }}\left[{\frac {3\mathbf {r} (\mathbf {m} \cdot \mathbf {r} )}{r^{5}}}-{\frac {\mathbf {m} }{r^{3}}}\right].$

সমানভাবে, যদি $\mathbf {r}$ অভিমুখে ইউনিট ভেক্টর $\mathbf {\hat {r}}$ হয়,

$\mathbf {B} ({\mathbf {r} })={\frac {\mu _{0}}{4\pi }}\left[{\frac {3\mathbf {\hat {r}} (\mathbf {m} \cdot \mathbf {\hat {r}} )-\mathbf {m} }{r^{3}}}\right].$

গোলকের স্থানাঙ্ক চৌম্বকীয় মুহুর্তের সাথে z-অক্ষের প্রান্তিককরণ করে যদি আমরা ব্যবহার করি $\mathbf {\hat {r}} \cos \theta -\mathbf {\hat {z}} =\sin \theta {\boldsymbol {\hat {\theta }}}$, তাহলে এই ভাবে সম্পর্কটি প্রকাশ করা যেতে পারে

$\mathbf {B} ({\mathbf {r} })={\frac {\mu _{0}|\mathbf {m} |}{4\pi r^{3}}}\left(2\cos \theta \,\mathbf {\hat {r}} +\sin \theta \,{\boldsymbol {\hat {\theta }}}\right).$

বিকল্পভাবে চৌম্বকীয় মেরু সীমা থেকে প্রথমে স্কেলার সম্ভাব্যতা পাওয়া যেতে পারে

$\psi ({\mathbf {r} })={\frac {{\mathbf {m} }\cdot {\mathbf {r} }}{4\pi r^{3}}},$

এবং তাই অ্যাম্পিয়ার-টার্ন মিটার প্রতি চৌম্বকীয় ক্ষেত্র শক্তি (বা এইচ-ফিল্ডের শক্তি) হ'ল

${\mathbf {H} }({\mathbf {r} })=-\nabla \psi ={\frac {1}{4\pi }}\left[{\frac {3\mathbf {\hat {r}} (\mathbf {m} \cdot \mathbf {\hat {r}} )-\mathbf {m} }{r^{3}}}\right]={\frac {\mathbf {B} }{\mu _{0}}}.$

চৌম্বকীয় ক্ষেত্রটি চৌম্বকীয় মুহুর্তের অক্ষটি সম্পর্কে আবর্তনের অধীনে প্রতিসম হয়।

একটি দ্বিমেরুর আভ্যন্তরীণ চৌম্বকীয় ক্ষেত্র

আরও দেখুন: চৌম্বক ভ্রামক § চৌম্বকীয় মেরুর সংজ্ঞা

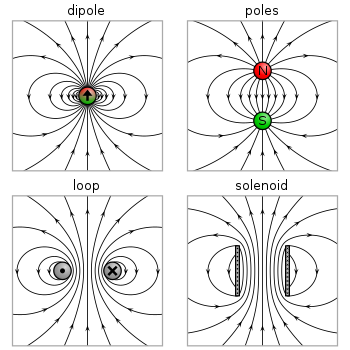
দ্বিমেরু (বর্তমান লুপ এবং চৌম্বকীয় মেরু) মডেলে উৎস থেকে দূরে চৌম্বকীয় ক্ষেত্রের জন্য একই পূর্বাভাস দেয়। তবে উৎস অঞ্চলের ভিতরে তারা বিভিন্ন পূর্বাভাস দেয়। দুই মেরুর মধ্যে চৌম্বক ক্ষেত্রটি চৌম্বকীয় মুহুর্তের বিপরীত দিকে থাকে (যা ঋণাত্মক আধান থেকে ধনাত্মক আধানের দিকে নির্দেশ করে)। যখন কোনও বর্তমান লুপের ভিতরে থাকে তখন এটি একই দিকে থাকে (ডানদিকে চিত্রটি দেখুন)। এই পার্থক্যটি কেবল তখনই গুরুত্বপূর্ণ যখন দ্বিমেরু সীমাটি চৌম্বকীয় উপাদানের অভ্যন্তরের ক্ষেত্রগুলি গণনা করতে ব্যবহৃত হয়।

প্রাবাহ এবং ক্ষেত্রের গুণফলকে স্থির রেখে যদি বর্তমান লুপটিকে আরও ছোট ও ছোট করে চৌম্বকীয় দ্বিমেরু গঠন করা হয় তবে সীমাবদ্ধ ক্ষেত্রটি হয়

$\mathbf {B} (\mathbf {r} )={\frac {\mu _{0}}{4\pi }}\left[{\frac {3\mathbf {\hat {r}} (\mathbf {\hat {r}} \cdot \mathbf {m} )-\mathbf {m} }{|\mathbf {r} |^{3}}}+{\frac {8\pi }{3}}\mathbf {m} \delta (\mathbf {r} )\right],$

যেখানে δ(r) হল ডিরাক ডেল্টা ফাংশন তিনটি মাত্রায়। এই সীমাটি দ্বিমেরুর অভ্যন্তরীণ ক্ষেত্রের জন্য সঠিক।

চৌম্বকীয় মেরু-চার্জ এবং দূরত্বের গুনফলকে স্থির রেখে যদি একটি "উত্তর মেরু" এবং "দক্ষিণ মেরু" নিয়ে একটি চৌম্বকীয় দ্বিমেরু গঠিত হয় এবং তাদের আরও কাছাকাছি আনা হতে থাকে তবে সীমিত ক্ষেত্রটি হবে

$\mathbf {H} (\mathbf {r} )={\frac {1}{4\pi }}\left[{\frac {3\mathbf {\hat {r}} (\mathbf {\hat {r}} \cdot \mathbf {m} )-\mathbf {m} }{|\mathbf {r} |^{3}}}-{\frac {4\pi }{3}}\mathbf {m} \delta (\mathbf {r} )\right].$

এই ক্ষেত্রগুলি B = μ₀(H + M) দ্বারা সম্পর্কিত যেখানে

$\mathbf {M} (\mathbf {r} )=\mathbf {m} \delta (\mathbf {r} )$ হ'ল চৌম্বকীয়করণ।

দুটি চৌম্বক দ্বিমেরুর মধ্যের বল

আরও দেখুন: চুম্বকের মধ্যে বল § চৌম্বকীয় দ্বিমেরুর-দ্বিমেরুর মিথষ্ক্রিয়া

একটি দ্বিমেরু মুহুর্ত m₁ একটি ভেক্টর r দ্বারা পৃথক করা স্থানে অপর একটি দ্বিমেরু m₂ এর উপর প্রয়োগ করলে প্রযুক্ত বল F গণনা করে বের করতে ব্যবহার যায়:

$\mathbf {F} =\nabla \left(\mathbf {m} _{2}\cdot \mathbf {B} _{1}\right),$

অথবা

$\mathbf {F} (\mathbf {r} ,\mathbf {m} _{1},\mathbf {m} _{2})={\dfrac {3\mu _{0}}{4\pi r^{5}}}\left[(\mathbf {m} _{1}\cdot \mathbf {r} )\mathbf {m} _{2}+(\mathbf {m} _{2}\cdot \mathbf {r} )\mathbf {m} _{1}+(\mathbf {m} _{1}\cdot \mathbf {m} _{2})\mathbf {r} -{\dfrac {5(\mathbf {m} _{1}\cdot \mathbf {r} )(\mathbf {m} _{2}\cdot \mathbf {r} )}{r^{2}}}\mathbf {r} \right],$

যেখানে r দ্বিমেরুর মধ্যের দূরত্ব। m₁ এর উপর প্রযুক্ত বল বিপরীত অভিমুখী হবে।

টর্ক বের করার সূত্রটি হবে

${\boldsymbol {\tau }}=\mathbf {m} _{2}\times \mathbf {B} _{1}.$

তথ্যসূত্র

• Chow, Tai L. (২০০৬)। Introduction to electromagnetic theory: a modern perspective। Jones & Bartlett Learning। আইএসবিএন ৯৭৮-০-৭৬৩৭-৩৮২৭-৩। {{বই উদ্ধৃতি}}: অবৈধ |সূত্র=harv (সাহায্য)
• Jackson, John D. (১৯৭৫)। Classical Electrodynamics (2nd সংস্করণ)। Wiley। আইএসবিএন ০-৪৭১-৪৩১৩২-X। {{বই উদ্ধৃতি}}: অবৈধ |সূত্র=harv (সাহায্য)
• Furlani, Edward P. (২০০১)। Permanent Magnet and Electromechanical Devices: Materials, Analysis, and Applications। Academic Press। আইএসবিএন ০-১২-২৬৯৯৫১-৩। {{বই উদ্ধৃতি}}: অবৈধ |সূত্র=harv (সাহায্য)