জ্যোতির্গতিবিজ্ঞান

জ্যোতির্গতিবিজ্ঞান বা অ্যাস্ট্রোডাইনামিক্স হল রকেট এবং অন্যান্য মহাকাশযানের গতি সংক্রান্ত ব্যবহারিক সমস্যাগুলির জন্য ব্যালিস্টিক ও মহাকাশীয় বলবিদ্যার প্রয়োগ। কোনো বস্তুর গতি সাধারণত নিউটনের গতির সূত্র ও সার্বজনীন মহাকর্ষের সূত্র এর মাধ্যমে নির্ণয় করা হয়। জ্যোতির্গতিবিজ্ঞান হল মহাকাশ-অনুসন্ধান ও নিয়ন্ত্রণের মধ্যেকার একটি মূল হাতিয়ার।
নক্ষত্রসমূহ, গ্রহ, চাঁদ ও ধূমকেতুর মতো প্রাকৃতিক জ্যোতির্বৈজ্ঞানিক বস্তু এবং মহাকাশযান উভয়ই মহাকর্ষের প্রভাবে নির্দিষ্ট কক্ষপথে বিচরণ করে। জ্যোতির্গতিবিজ্ঞান মহাকাশযানের গতিপথের নির্ণয়, যার মধ্যে অরবিটাল ম্যানুভার, অরবিটাল প্লেনের পরিবর্তন এমনকি আন্তঃযোগাযোগ রক্ষায় রয়েছে এর ভূমিকা এবং মিশন পরিকল্পনাকারীরা প্রপালসিভ ম্যানুভারের ফলাফলের পূর্বাভাস দিতে এটি ব্যবহার করেন।
ইতিহাস[সম্পাদনা]
বিংশ শতাব্দীতে মহাকাশ ভ্রমণের উত্থানের আগ পর্যন্ত, কক্ষপথ এবং মহাকাশীয় মেকানিক্সের মধ্যে সামান্য পার্থক্য ছিল। স্পুটনিকের সময়ে, ক্ষেত্রটিকে 'স্পেস ডাইনামিকস' বলা হত।[১] মৌলিক কৌশলগুলি, যেমন কেপলারিয়ান সমস্যা সমাধানের জন্য ব্যবহৃত হয় (সময়ের ফাংশন হিসাবে অবস্থান নির্ধারণ), তাই উভয় ক্ষেত্রেই একই। অধিকন্তু, ক্ষেত্রগুলির ইতিহাস প্রায় সম্পূর্ণ ভাগ করা হয়।
জোহানেস কেপলার সর্বপ্রথম সফলভাবে গ্রহের কক্ষপথকে উচ্চ মাত্রার নির্ভুলতার সাথে মডেল করেছিলেন, ১৬০৫ সালে তার আইন প্রকাশ করেছিলেন। আইজ্যাক নিউটন Philosophiæ Naturalis Principia Mathematica-এর প্রথম সংস্করণে মহাকাশীয় গতির আরও সাধারণ নিয়ম প্রকাশ করেছিলেন, যা একটি পদ্ধতি দিয়েছিল (১৬৮৭) তিনটি পর্যবেক্ষণ থেকে একটি প্যারাবলিক পথ অনুসরণ করে একটি শরীরের কক্ষপথ খুঁজে পাওয়া।[২] এটি এডমন্ড হ্যালি বিভিন্ন ধূমকেতুর কক্ষপথ স্থাপন করতে ব্যবহার করেছিলেন, যার মধ্যে তার নাম রয়েছে। ১৭৭৪ সালে লিওনহার্ড অয়লার দ্বারা নিউটনের ক্রমাগত আনুমানিক পদ্ধতিকে একটি বিশ্লেষণী পদ্ধতিতে রূপান্তরিত করা হয়েছিল, যার কাজটি ১৭৬১-১৭৭৭ সালে জোহান ল্যাম্বার্ট দ্বারা উপবৃত্তাকার এবং হাইপারবোলিক কক্ষপথে সাধারণীকরণ করা হয়েছিল।
কক্ষপথ নির্ধারণের আরেকটি মাইলফলক ছিল ১৮০১ সালে বামন গ্রহ সেরেস এর "পুনরুদ্ধার"-এ কার্ল ফ্রেডরিখ গাউসের সহায়তা। গাউসের পদ্ধতিটি ছয়টি বা বিট খুঁজে বের করতে মাত্র তিনটি পর্যবেক্ষণ (ডান অ্যাসেনশন এবং ডিক্লিনেশনের জোড়া আকারে) ব্যবহার করতে সক্ষম হয়েছিল। উপাদান যা সম্পূর্ণরূপে একটি কক্ষপথ বর্ণনা করে। কক্ষপথ নির্ধারণের তত্ত্বটি পরবর্তীকালে এমন পর্যায়ে বিকশিত হয়েছে যেখানে আজ এটি জিপিএস রিসিভারের পাশাপাশি নতুন পর্যবেক্ষণ করা ছোট ছোট গ্রহগুলির ট্র্যাকিং এবং তালিকাভুক্তিতে প্রয়োগ করা হয়। আধুনিক কক্ষপথ নির্ধারণ এবং ভবিষ্যদ্বাণী সমস্ত ধরণের উপগ্রহ এবং স্পেস প্রোব পরিচালনা করতে ব্যবহৃত হয়, কারণ তাদের ভবিষ্যত অবস্থানগুলি উচ্চ মাত্রায় নির্ভুলতা জানা প্রয়োজন।
জ্যোতির্বিজ্ঞানী স্যামুয়েল হেরিক ১৯৩০ এর দশকের শুরুতে অ্যাস্ট্রোডাইনামিকস তৈরি করেছিলেন। তিনি রকেট বিজ্ঞানী রবার্ট গডার্ড এর সাথে পরামর্শ করেছিলেন এবং মহাকাশ নেভিগেশন কৌশলগুলির উপর তার কাজ চালিয়ে যাওয়ার জন্য উত্সাহিত করেছিলেন, কারণ গডার্ড বিশ্বাস করেছিলেন যে ভবিষ্যতে তাদের প্রয়োজন হবে। ১৯৬০-এর দশকে অ্যাস্ট্রোডাইনামিকসের সংখ্যাসূচক কৌশলগুলি নতুন শক্তিশালী কম্পিউটারগুলির সাথে মিলিত হয়েছিল, এবং মানুষ চাঁদে ভ্রমণ এবং ফিরে আসার জন্য প্রস্তুত ছিল।
ব্যবহারিক কৌশল[সম্পাদনা]
চলতি নিয়ম[সম্পাদনা]
নীচের নির্দেশিত অ্যাস্ট্রোডাইনামিকসের মানক অনুমানের অধীনে ক্লাসিক্যাল মেকানিক্স দ্বারা আনুমানিক পরিস্থিতিগুলির জন্য নিম্নোক্ত নিয়মগুলি কার্যকর । আলোচিত সুনির্দিষ্ট উদাহরণ হল একটি উপগ্রহ একটি গ্রহকে প্রদক্ষিণ করছে, তবে অঙ্গুষ্ঠের নিয়মগুলি অন্যান্য পরিস্থিতিতেও প্রযোজ্য হতে পারে, যেমন সূর্যের মতো একটি নক্ষত্রের চারপাশে ছোট দেহের কক্ষপথ।
- কেপলারের গ্রহের গতির সূত্র :
- কক্ষপথগুলি উপবৃত্তাকার , উপবৃত্তের একটি ফোকাসে ভারী শরীর সহ । এর একটি বিশেষ ক্ষেত্রে একটি বৃত্তাকার কক্ষপথ (একটি বৃত্ত হল উপবৃত্তের একটি বিশেষ ক্ষেত্রে) যার কেন্দ্রে গ্রহ রয়েছে।
- গ্রহ থেকে উপগ্রহে টানা একটি রেখা সমান সময়ে সমান অঞ্চলগুলিকে পরিমাপ করে , কক্ষপথের যে অংশটি পরিমাপ করা হোক না কেন।
- একটি উপগ্রহের কক্ষপথের বর্গ গ্রহ থেকে তার গড় দূরত্বের ঘনক্ষেত্রের সমানুপাতিক।
- বল প্রয়োগ না করে (যেমন রকেট ইঞ্জিন নিক্ষেপ করা) স্যাটেলাইটের কক্ষপথের সময়কাল এবং আকৃতি পরিবর্তন হবে না।
- একটি নিম্ন কক্ষপথে একটি উপগ্রহ (বা একটি উপবৃত্তাকার কক্ষপথের একটি নিম্ন অংশ) একটি উচ্চতর কক্ষপথে (বা একটি উপবৃত্তাকার কক্ষপথের একটি উচ্চ অংশ) উপগ্রহের তুলনায় গ্রহের পৃষ্ঠের সাপেক্ষে আরও দ্রুত গতিতে চলে, শক্তিশালী মহাকর্ষীয় কারণে। গ্রহের কাছাকাছি আকর্ষণ।
- যদি উপগ্রহের কক্ষপথে শুধুমাত্র একটি বিন্দুতে থ্রাস্ট প্রয়োগ করা হয়, তবে এটি প্রতিটি পরবর্তী কক্ষপথে একই বিন্দুতে ফিরে আসবে, যদিও এর বাকি পথ পরিবর্তিত হবে। এইভাবে শুধুমাত্র একটি সংক্ষিপ্ত থ্রাস্ট প্রয়োগের মাধ্যমে একটি বৃত্তাকার কক্ষপথ থেকে অন্যটিতে যেতে পারে না।
- একটি বৃত্তাকার কক্ষপথ থেকে, উপগ্রহের গতির বিপরীত দিকে প্রয়োগ করা থ্রাস্ট কক্ষপথটিকে উপবৃত্তাকারে পরিবর্তন করে; স্যাটেলাইটটি নেমে আসবে এবং ফায়ারিং পয়েন্ট থেকে ১৮০ ডিগ্রি দূরে সর্বনিম্ন অরবিটাল পয়েন্টে ( পেরিয়েপাস ) পৌঁছাবে; তারপর এটি ফিরে আসবে। স্যাটেলাইটের গতির দিকে প্রয়োগ করা থ্রাস্ট ফায়ারিং পয়েন্ট থেকে ১৮০ ডিগ্রি দূরে তার সর্বোচ্চ বিন্দু ( অপদূরবিন্দু ) সহ একটি উপবৃত্তাকার কক্ষপথ তৈরি করে।
অরবিটাল মেকানিক্সের নিয়মের পরিণতি কখনও কখনও পাল্টা স্বজ্ঞাত হয়। উদাহরণস্বরূপ, যদি দুটি মহাকাশযান একই বৃত্তাকার কক্ষপথে থাকে এবং ডক করতে চায়, যদি না তারা খুব কাছাকাছি না থাকে, তাহলে ট্রেলিং ক্রাফটটি দ্রুত যাওয়ার জন্য তার ইঞ্জিনগুলিকে কেবল ফায়ার করতে পারে না। এটি তার কক্ষপথের আকৃতি পরিবর্তন করবে, যার ফলে এটি উচ্চতা অর্জন করবে এবং প্রকৃতপক্ষে নেতৃস্থানীয় নৈপুণ্যের তুলনায় ধীর হয়ে যাবে, লক্ষ্যটি হারিয়ে যাবে। ডকিং করার আগে স্থান মিলনের জন্য সাধারণত একাধিক অরবিটাল পিরিয়ডে একাধিক সুনির্দিষ্টভাবে গণনা করা ইঞ্জিন ফায়ারিং লাগে, এটি সম্পূর্ণ হতে কয়েক ঘন্টা বা এমনকি দিনও প্রয়োজন।
অ্যাস্ট্রোডাইনামিকসের মানক অনুমানগুলি যে পরিমাণে ধরে না, প্রকৃত ট্র্যাজেক্টোরিগুলি গণনা করা থেকে পরিবর্তিত হবে। উদাহরণস্বরূপ, নিম্ন পৃথিবীর কক্ষপথে থাকা বস্তুর জন্য সাধারণ বায়ুমণ্ডলীয় টানা আরেকটি জটিল কারণ ।
বাইনারি স্টার সিস্টেমের মতো একই ভরের দুই বা ততোধিক দেহের বর্ণনা করার সময় থাম্বের এই নিয়মগুলি নিশ্চিতভাবে ভুল হয় (দেখুন n-বডি সমস্যা )। সেলেস্টিয়াল মেকানিক্স বিস্তৃত বিভিন্ন পরিস্থিতিতে প্রযোজ্য আরও সাধারণ নিয়ম ব্যবহার করে। কেপলারের গ্রহের গতির সূত্র, যা গাণিতিকভাবে নিউটনের সূত্র থেকে প্রাপ্ত হতে পারে, শুধুমাত্র অ-মাধ্যাকর্ষণ শক্তির অনুপস্থিতিতে দুটি মহাকর্ষীয় বস্তুর গতি বর্ণনা করার ক্ষেত্রে কঠোরভাবে ধরে রাখে; তারা প্যারাবোলিক এবং হাইপারবোলিক ট্রাজেক্টোরিও বর্ণনা করে। তারার মতো বৃহৎ বস্তুর সান্নিধ্যে ক্লাসিক্যাল মেকানিক্স এবং সাধারণ আপেক্ষিকতার মধ্যে পার্থক্যও গুরুত্বপূর্ণ হয়ে ওঠে।
জ্যোতির্গতিবিদ্যার সমীকরণসমূহ[সম্পাদনা]
জ্যোতির্গতিবিদ্যার মৌলিক নিয়ম হল নিউটনের সার্বজনীন মহাকর্ষের সূত্র ও নিউটনের গতির সূত্র, যখন মৌলিক গাণিতিক হাতিয়ার হল ডিফারেনশিয়াল ক্যালকুলাস।
বায়ুমণ্ডলের বাইরের প্রতিটি কক্ষপথ এবং গতিপথ নীতিগতভাবে বিপরীতমুখী, অর্থাৎ স্থান-কাল ফাংশনে সময় বিপরীত হয়। বেগ বিপরীত হয় ও ত্বরণ একই, রকেট বিস্ফোরণের কারণেও। এইভাবে যদি একটি রকেট বিস্ফোরণ বেগের দিকে থাকে তবে বিপরীত ক্ষেত্রে এটি বেগের বিপরীত। অবশ্যই রকেট বিস্ফোরণের ক্ষেত্রে ইভেন্টগুলির সম্পূর্ণ বিপরীতমুখী হয় না, উভয় উপায়ে একই ডেল্টা-ভি ব্যবহার করা হয় এবং একই ভর অনুপাত প্রযোজ্য।
অ্যাস্ট্রোডাইনামিকসের মানক অনুমানগুলির মধ্যে রয়েছে বাইরের দেহ থেকে অ-হস্তক্ষেপ, একটি দেহের জন্য নগণ্য ভর, এবং নগণ্য অন্যান্য শক্তি (যেমন সৌর বায়ু, বায়ুমণ্ডলীয় টানা ইত্যাদি)। এই সরলীকরণ অনুমানগুলি ছাড়াই আরও সঠিক গণনা করা যেতে পারে, তবে সেগুলি আরও জটিল। বর্ধিত নির্ভুলতা প্রায়শই সার্থক হওয়ার জন্য গণনায় যথেষ্ট পার্থক্য তৈরি করে না।
কেপলারের গ্রহের গতির সূত্র নিউটনের সূত্র থেকে প্রাপ্ত হতে পারে, যখন এটা ধরে নেওয়া হয় যে প্রদক্ষিণকারী দেহটি শুধুমাত্র কেন্দ্রীয় আকর্ষণের মহাকর্ষীয় শক্তির অধীন। যখন একটি ইঞ্জিন থ্রাস্ট বা প্রপালসিভ ফোর্স উপস্থিত থাকে, তখনও নিউটনের আইন প্রযোজ্য হয়, কিন্তু কেপলারের আইন বাতিল হয়ে যায়। যখন থ্রাস্ট থেমে যায়, ফলস্বরূপ কক্ষপথ ভিন্ন হবে কিন্তু কেপলারের আইন দ্বারা আবার বর্ণনা করা হবে যা উপরে সেট করা হয়েছে। তিনটি আইন হল:
- প্রতিটি গ্রহের কক্ষপথ একটি কেন্দ্রবিন্দুতে সূর্যের সাথে একটি উপবৃত্ত।
- একটি গ্রহ এবং সূর্যের সাথে মিলিত একটি রেখা সমান সময়ের ব্যবধানে সমান অঞ্চলগুলিকে সরিয়ে দেয়।
- গ্রহের কক্ষপথের সময়কালের বর্গগুলি কক্ষপথের আধা - প্রধান অক্ষের ঘনক্ষেত্রগুলির সাথে সরাসরি সমানুপাতিক।
মুক্তিবেগ[সম্পাদনা]
একটি অব্যাহতি বেগ জন্য সূত্র নিম্নলিখিত হিসাবে উদ্ভূত হয়। যেকোনো মহাকাশ যানের নির্দিষ্ট শক্তি (প্রতি ইউনিট ভরের শক্তি) দুটি উপাদান, নির্দিষ্ট সম্ভাব্য শক্তি এবং নির্দিষ্ট গতিশক্তি দ্বারা গঠিত । M ভরের একটি গ্রহের সাথে যুক্ত নির্দিষ্ট সম্ভাব্য শক্তি দ্বারা দেওয়া হয়
যেখানে G হল মহাকর্ষীয় ধ্রুবক এবং r হল দুটি দেহের মধ্যে দূরত্ব;
যখন একটি বস্তুর নির্দিষ্ট গতিশক্তি দ্বারা দেওয়া হয়
যেখানে v এর গতি;
এবং তাই মোট নির্দিষ্ট কক্ষপথ শক্তি
যেহেতু শক্তি সংরক্ষিত হয় E, দূরত্বের উপর নির্ভর করতে পারে না,r, কেন্দ্রীয় বডির কেন্দ্র থেকে প্রশ্নে থাকা মহাকাশ যান পর্যন্ত, অর্থাৎ নির্দিষ্ট কক্ষপথের শক্তিকে স্থির রাখতে v অবশ্যই r এর সাথে পরিবর্তিত হবে। অতএব, বস্তু অসীম পৌঁছতে পারেশুধুমাত্র যদি এই পরিমাণ অঋণাত্মক হয়, যা বোঝায়
পৃথিবীর পৃষ্ঠ থেকে পালানোর বেগ প্রায় ১১ কিমি/সেকেন্ড, কিন্তু সূর্যের মহাকর্ষীয় টানের কারণে এটি শরীরকে অসীম দূরত্বে পাঠানোর জন্য অপর্যাপ্ত। সূর্য-পৃথিবীর সমান দূরত্ব থেকে সূর্য-পৃথিবীর সমান দূরত্বে অবস্থান থেকে সৌরজগৎ থেকে পালানোর জন্য, কিন্তু পৃথিবীর কাছাকাছি নয়, প্রায় ৪২ কিমি/সেকেন্ড বেগ প্রয়োজন, তবে পৃথিবীর কক্ষপথের বেগের জন্য "আংশিক কৃতিত্ব" থাকবে পৃথিবী থেকে উৎক্ষেপিত মহাকাশযানের জন্য, যদি তাদের আরও ত্বরণ (প্রপালশন সিস্টেমের কারণে) পৃথিবী তার কক্ষপথে ভ্রমণ করার সময় তাদের একই দিকে বহন করে।
মুক্ত কক্ষপথের জন্য সূত্র[সম্পাদনা]
কক্ষপথগুলি কনিক বিভাগ , তাই একটি প্রদত্ত কোণের জন্য একটি দেহের দূরত্বের সূত্রটি মেরু স্থানাঙ্কের সেই বক্ররেখার সূত্রের সাথে মিলে যায়, যা হল:
মহাকর্ষীয় পরামিতি বলা হয় ।এবং m1 এবং m2বস্তুর ভর, 1 এবং 2 বস্তু h এর সাপেক্ষে অবজেক্ট 2 এর 1 নির্দিষ্ট কৌণিক ভরবেগ। প্যারামিটার সত্য অসঙ্গতি হিসাবে পরিচিত, p সেমি লাটাস রেকটাম হয় , যখন অরবিটাল বিকেন্দ্রিকতা , যা ছয়টি স্বাধীন অরবিটাল উপাদানের বিভিন্ন রূপ থেকে পাওয়া যায়।
বৃত্তাকার কক্ষপথ[সম্পাদনা]
সমস্ত আবদ্ধ কক্ষপথ যেখানে একটি কেন্দ্রীয় দেহের মাধ্যাকর্ষণ প্রাধান্য পায় সেগুলি উপবৃত্তাকার প্রকৃতির। এর একটি বিশেষ ক্ষেত্রে বৃত্তাকার কক্ষপথ, যা শূন্য বিকেন্দ্রিকতার একটি উপবৃত্ত। ভর M এর মাধ্যাকর্ষণ কেন্দ্র থেকে r দূরত্বে একটি বৃত্তাকার কক্ষপথে একটি দেহের বেগের সূত্রটি নিম্নরূপ পাওয়া যেতে পারে:
কেন্দ্রাতিগ ত্বরণ মহাকর্ষের কারণে ত্বরণের সাথে মিলে যায়।
তাই,
যেখানে G মহাকর্ষীয় ধ্রুবক , সমান
- 6.6743 × 10 −11 m 3 /(kg·s 2 )
এই সূত্রটি সঠিকভাবে ব্যবহার করার জন্য, ইউনিটগুলি সামঞ্জস্যপূর্ণ হতে হবে; উদাহরণ স্বরূপ, M কিলোগ্রাম হতে হবে, এবং r মিটার হতে হবে। উত্তর হবে মিটার প্রতি সেকেন্ডে।
পরিমাণ GM এটিকে প্রায়শই আদর্শ মহাকর্ষীয় পরামিতি বলা হয়, যার সৌরজগতের প্রতিটি গ্রহ বা চাঁদের জন্য আলাদা মান রয়েছে ।
একবার বৃত্তাকার কক্ষপথের বেগ জানা হয়ে গেলে, পালাবার বেগ সহজেই পাওয়া যায় দ্বারা গুণ করে:
মাধ্যাকর্ষণ থেকে বাঁচতে, গতিশক্তিকে অন্তত নেতিবাচক সম্ভাব্য শক্তির সাথে মেলে। অতএব,
উপবৃত্তাকার কক্ষপথ[সম্পাদনা]
যদি, তাহলে মুক্ত কক্ষপথের সমীকরণের হর প্রকৃত অসঙ্গতির সাথে পরিবর্তিত হয়, কিন্তু ইতিবাচক থেকে যায়, কখনো শূন্য হয় না। অতএব, আপেক্ষিক অবস্থান ভেক্টর আবদ্ধ থাকে, পেরিয়াপিসিসে এর ক্ষুদ্রতম মাত্রা থাকে, যা দ্বারা দেওয়া হয়:
সর্বোচ্চ মান r পৌঁছানো হয় যখন এই বিন্দুটিকে বলা হয় apoapsis, এবং এর রেডিয়াল স্থানাঙ্ক, নির্দেশিত, হয়
2a পেরিয়াপসিস থেকে apse লাইন বরাবর পরিমাপ করা দূরত্ব হবে P apoapsis A, নীচের সমীকরণে চিত্রিত হিসাবে:
উপরের সমীকরণগুলি প্রতিস্থাপন করে, আমরা পাই:
a হল উপবৃত্তের অর্ধপ্রধান অক্ষ। P এর জন্য সমাধান, এবং উপরের কনিক বিভাগের বক্ররেখা সূত্রে ফলাফল প্রতিস্থাপন করে, আমরা পাই:
অরবিটাল কৌশল[সম্পাদনা]
স্পেসফ্লাইটে , একটি অরবিটাল ম্যানুভার হল একটি মহাকাশযানের কক্ষপথ পরিবর্তন করতে প্রপালশন সিস্টেমের ব্যবহার । পৃথিবী থেকে দূরে মহাকাশযানের জন্য-উদাহরণস্বরূপ সূর্যের চারপাশে কক্ষপথে থাকা-একটি অরবিটাল ম্যানুভারকে ডিপ-স্পেস ম্যানুভার (DSM) বলা হয় । [ শরীরে যাচাই করা হয়নি ]
অরবিটাল স্থানান্তর[সম্পাদনা]
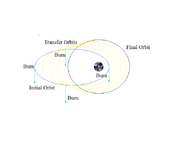
স্থানান্তর কক্ষপথগুলি সাধারণত উপবৃত্তাকার কক্ষপথ যা মহাকাশযানকে একটি (সাধারণত উল্লেখযোগ্যভাবে বৃত্তাকার) কক্ষপথ থেকে অন্য কক্ষপথে যেতে দেয়। সাধারণত তাদের শুরুতে পোড়া, শেষে পোড়া এবং মাঝে মাঝে এক বা একাধিক পোড়ার প্রয়োজন হয়।
- Hohmann স্থানান্তর কক্ষপথের একটি ন্যূনতম ডেল্টা-v প্রয়োজন ।
- কক্ষপথের অনুপাত ১১.৯৪ বা তার বেশি হলে একটি দ্বি-উপবৃত্তীয় স্থানান্তরের জন্য Hohmann স্থানান্তরের চেয়ে কম শক্তির প্রয়োজন হতে পারে,[৩] তবে Hohmann স্থানান্তরের সময় বর্ধিত ট্রিপ সময়ের খরচে আসে।
- দ্রুত স্থানান্তরগুলি উচ্চ ডেল্টা-ভি খরচে মূল এবং গন্তব্য উভয় কক্ষপথকে ছেদ করে এমন কোনও কক্ষপথ ব্যবহার করতে পারে।
- কম থ্রাস্ট ইঞ্জিন (যেমন বৈদ্যুতিক চালনা ) ব্যবহার করে, যদি প্রাথমিক কক্ষপথটি চূড়ান্ত কাঙ্ক্ষিত বৃত্তাকার কক্ষপথের সাথে সুপারসিঙ্ক্রোনাস হয় তবে এপোজিতে বেগের দিকে ক্রমাগত থ্রাস্ট করে সর্বোত্তম স্থানান্তর কক্ষপথটি অর্জন করা হয়। তবে কম থ্রাস্টের কারণে এই পদ্ধতিটি অনেক বেশি সময় নেয়।
নন-কপ্ল্যানার কক্ষপথের মধ্যে অরবিটাল স্থানান্তরের ক্ষেত্রে, প্লেনের থ্রাস্ট পরিবর্তনঅরবিটাল প্লেনগুলিকে ছেদ করে এমন বিন্দুতে তৈরি করা আবশ্যক ("নোড")। যেহেতু উদ্দেশ্য হল প্লেনের মধ্যবর্তী কোণের সমান একটি কোণ দ্বারা বেগ ভেক্টরের দিক পরিবর্তন করা, এই থ্রাস্টের প্রায় পুরোটাই তৈরি করা উচিত যখন মহাকাশযানটি apoapse এর কাছাকাছি নোডে থাকে, যখন বেগ ভেক্টরের মাত্রা তার সর্বনিম্ন এ যাইহোক, অরবিটাল প্রবণতা পরিবর্তনের একটি ছোট ভগ্নাংশ পেরিয়াপসের কাছাকাছি নোডে করা যেতে পারে, কাঙ্ক্ষিত প্রবণতা পরিবর্তনের দিকে স্থানান্তর কক্ষপথ ইনজেকশন থ্রাস্টকে সামান্য কোণ করে। এটি কাজ করে কারণ একটি ছোট কোণের কোসাইন প্রায় এক, যার ফলে পেরিয়াপসের কাছে মহাকাশযানের উচ্চ বেগ থাকা সত্ত্বেও ছোট সমতল পরিবর্তন কার্যকরভাবে "মুক্ত" হয়, কারণ ওবার্থ প্রভাব বৃদ্ধির কারণে,
চিত্রগুলোতে:-
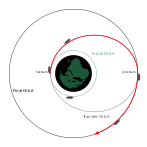
→একটি Hohmann একটি নিম্ন বৃত্তাকার কক্ষপথ থেকে একটি উচ্চ বৃত্তাকার কক্ষপথে স্থানান্তর
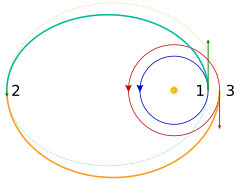
→একটি নিম্ন বৃত্তাকার প্রারম্ভিক কক্ষপথ (গাঢ় নীল) থেকে একটি উচ্চ বৃত্তাকার কক্ষপথে (লাল) একটি দ্বি-উপবৃত্ত স্থানান্তর
→দুটি বৃত্তাকার কক্ষপথের মধ্যে সাধারণ দুই-আবেগ উপবৃত্তাকার স্থানান্তর
→একটি নিম্ন বৃত্তাকার কক্ষপথ থেকে একটি উচ্চ বৃত্তাকার কক্ষপথে একটি সাধারণ স্থানান্তর
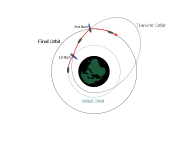
→বৈদ্যুতিক চালনা ব্যবহার করে একটি সুপারসিঙ্ক্রোনাস থেকে জিওসিঙ্ক্রোনাস কক্ষপথে একটি উপগ্রহ স্থানান্তর করার জন্য একটি সর্বোত্তম ক্রম
মাধ্যাকর্ষণ সহায়তা এবং ওবার্থ প্রভাব[সম্পাদনা]
একটি মহাকর্ষ সহায়তায় , একটি মহাকাশযান একটি গ্রহের দ্বারা দুলছে এবং একটি ভিন্ন দিকে, ভিন্ন গতিতে ছেড়ে যায়। এটি আরও জ্বালানী বহন করার পরিবর্তে একটি মহাকাশযানকে গতি বা ধীর করতে কার্যকর।
এই কৌশলটি বড় দূরত্বে একটি ইলাস্টিক সংঘর্ষের মাধ্যমে আনুমানিক করা যেতে পারে , যদিও ফ্লাইবাই কোনো শারীরিক যোগাযোগের সাথে জড়িত নয়। নিউটনের তৃতীয় সূত্রের (সমান এবং বিপরীত প্রতিক্রিয়া) কারণে, একটি মহাকাশযান দ্বারা অর্জিত যে কোনও গতি অবশ্যই গ্রহের দ্বারা হারিয়ে যেতে হবে, বা এর বিপরীতে। যাইহোক, যেহেতু গ্রহটি মহাকাশযানের চেয়ে অনেক বেশি, অনেক বেশি বিশাল, গ্রহটির কক্ষপথে প্রভাব নগণ্য।
Oberth প্রভাব নিযুক্ত করা যেতে পারে, বিশেষ করে একটি অভিকর্ষ সহায়তা অপারেশন সময়. এই প্রভাবটি হল যে একটি প্রপালশন সিস্টেমের ব্যবহার উচ্চ গতিতে আরও ভাল কাজ করে, এবং তাই একটি মহাকর্ষীয় দেহের কাছাকাছি থাকাকালীন কোর্স পরিবর্তনগুলি সবচেয়ে ভাল হয়; এটি কার্যকর ডেল্টা-ভি গুণ করতে পারে ।
ইন্টারপ্ল্যানেটারি ট্রান্সপোর্ট নেটওয়ার্ক এবং অস্পষ্ট কক্ষপথ[সম্পাদনা]
সৌরজগতের গ্রহ এবং চাঁদের মাধ্যাকর্ষণে অরৈখিকতা ব্যবহার করে রুট অনুসন্ধান করতে কম্পিউটার ব্যবহার করা এখন সম্ভব। উদাহরণস্বরূপ, পৃথিবীর উচ্চ কক্ষপথ থেকে মঙ্গল গ্রহে একটি কক্ষপথ প্লট করা সম্ভব, যা পৃথিবীর ট্রোজান পয়েন্টগুলির একটির কাছাকাছি চলে যায় । [ উদ্ধৃতি প্রয়োজন ] ইন্টারপ্ল্যানেটারি ট্রান্সপোর্ট নেটওয়ার্ক হিসাবে উল্লেখ করা হয় , এই অত্যন্ত বিশৃঙ্খল, এমনকি বিশৃঙ্খল, কক্ষপথের গতিপথের জন্য নীতিগতভাবে ল্যাগ্রেঞ্জ পয়েন্টে পৌঁছানোর জন্য প্রয়োজনের বাইরে কোনো জ্বালানির প্রয়োজন হয় না (অভ্যাসগতভাবে ট্র্যাজেক্টোরি বজায় রাখার জন্য কিছু কোর্স সংশোধন প্রয়োজন)। তাদের সাথে সবচেয়ে বড় সমস্যা হল তারা অত্যন্ত ধীর হতে পারে, অনেক বছর সময় নেয়। উপরন্তু লঞ্চ উইন্ডো অনেক দূরে হতে পারে.
তারা অবশ্য জেনেসিসের মতো প্রকল্পে নিযুক্ত হয়েছে । এই মহাকাশযানটি পৃথিবী-সূর্য এল 1 বিন্দু পরিদর্শন করেছে এবং খুব কম প্রপেলান্ট ব্যবহার করে ফিরে এসেছে।
আরও দেখুন[সম্পাদনা]
তথ্যসূত্র[সম্পাদনা]
- ↑ Hilton, W. F. (1962-05)। "Introduction to Space Dynamics. William Tyrrell Thomson. John Wiley, London. 1961. 317 pp. Diagrams. 87s."। Aeronautical Quarterly। 13 (2): 201–202। আইএসএসএন 0001-9259। ডিওআই:10.1017/s0001925900002390। line feed character in
|শিরোনাম=at position 33 (সাহায্য); এখানে তারিখের মান পরীক্ষা করুন:|তারিখ=(সাহায্য) - ↑ Bate, Roger (১৯৭১)। Fundamentals of astrodynamics। Donald D. Mueller, Jerry E. White। New York। আইএসবিএন 0-486-60061-0। ওসিএলসি 150036।
- ↑ Vallado, David A. (২০০১)। Fundamentals of astrodynamics and applications। Wayne D. McClain (2nd ed সংস্করণ)। Dordrecht: Kluwer Academic Publishers। আইএসবিএন 0-7923-6903-3। ওসিএলসি 47045147।