নির্ভরণ বিশ্লেষণ
| নির্ভরণ বিশ্লেষণ |
|---|
| পরিসংখ্যান সিরিজের একটি অংশ |
 |
| মডেল |
| প্রাক্কলন |
| পটভূমি |
|
|
পরিসংখ্যানিক প্রতিমান নির্মাণে নির্ভরণ বিশ্লেষণ (ইংরেজি: Regression Analysis) হচ্ছে কতগুলো পরিসংখ্যানিক প্রক্রিয়ার সমষ্টি যার মাধ্যমে চলকসমূহের মধ্যে বিদ্যমান সম্পর্ক নির্ণয় করা হয়। কতগুলো চলকের প্রতিমান নির্মাণ (মডেলিং) ও বিশ্লেষণের জন্য এতে অনেকগুলি কৌশল অন্তর্ভুক্ত রয়েছে, যেখানে মূল লক্ষ্য হচ্ছে একটি অধীন চলকের সাথে এক বা একাধিক স্বাধীন চলকের (বা 'সূচক') মধ্যকার সম্পর্ক নির্ণয়। আরও সুনির্দিষ্টভাবে বললে, যে কোনও একটি স্বাধীন চলকের মান পরিবর্তন করলে এবং অন্যান্য স্বাধীন চলকসমূহকে স্থির রাখলে, সাধারণত কীভাবে অধীন চলকটির (বা 'নির্ণায়ক চলক') মানের পরিবর্তন হয়, নির্ভরণ বিশ্লেষণ তা বুঝতে সাহায্য করে।
সচরাচর, নির্ভরণ বিশ্লেষণে স্বাধীন চলকসমূহ দেওয়া থাকলে অধীন চলকটির শর্তসাপেক্ষ সম্ভাব্য মান অনুমান করা হয় --- অর্থাৎ, স্বাধীন চলকগুলির মান স্থির থাকলে অধীন চলকের গড় মান অনুমান করা হয়। অসচরাচরভাবে, স্বাধীন চলক দেওয়া থাকলে অধীন চলকের শর্তসাপেক্ষ বণ্টনের সমাংশক (quantile) বা অন্য কোনও অবস্থানসূচক পরামিতির ওপর মনোযোগ দেওয়া হয়। সবক্ষেত্রেই, স্বাধীন চলকসমূহ নিয়ে গঠিত নির্ভরণ অপেক্ষকের (Regression function "রিগ্রেশন ফাংশন") মান নির্ণয় করতে হয়। নির্ভরণ বিশ্লেষণে আরেকটি আগ্রহের বিষয় হচ্ছে, কোন সম্ভাবনা-বণ্টন পদ্ধতি ব্যবহার করে নির্ভরণ ফাংশনের পূর্বানুমানের সাথে অধীন চলকের মানের ভিন্নতা চিহ্নিত করা। একটি সংশ্লিষ্ট কিন্তু স্বতন্ত্র উপায় হচ্ছে আবশ্যকীয় শর্ত বিশ্লেষণ (NCA: Necessary Condition Analysis)[১], যা স্বাধীন চলকের কোন্ মানটি, অধীন চলকের কোন প্রদত্ত মানের জন্য আবশ্যকীয়, কিন্তু পর্যাপ্ত নয়- তা শনাক্ত করার জন্য, স্বাধীন চলকের কোন প্রদত্ত মানের প্রেক্ষিতে, অধীন চলকের সর্বোচ্চ মান (গড় মানের পরিবর্তে) অনুমান করে (সিলিং রেখা বা সর্বোচ্চ-সীমা রেখা, মধ্যবর্তী রেখা নয়)।
পূর্বানুমান ও ভবিষ্যদ্বাণী করার জন্য নির্ভরণ বিশ্লেষণ ব্যাপকভাবে ব্যবহৃত হয়, যেখানে এর ব্যবহারের সাথে মেশিন লার্নিং ক্ষেত্রটির যথেষ্ট মিল রয়েছে। নির্ভরণ বিশ্লেষণ ব্যবহার করে, স্বাধীন চলকগুলির কোনগুলো আসলে অধীন চলকের সাথে সম্পর্কিত, এবং এই সম্পর্কগুলোর রূপ অনুসন্ধান করা যায়। সীমাবদ্ধ ক্ষেত্রে, স্বাধীন ও অধীন চলকের মধ্যে কার্যকারণ সম্পর্ক (causal relationships) অনুমান করার জন্য নির্ভরণ বিশ্লেষণ ব্যবহার করা যেতে পারে। তবে, এ থেকে ভ্রান্ত বা মিথ্যা সম্পর্ক পাওয়া যেতে পারে, সুতরাং সতর্কতা অবলম্বন করা সমীচীন।
নির্ভরণ বিশ্লেষণের জন্য অনেকগুলো পদ্ধতির বিকাশ ঘটেছে। পরিচিত পদ্ধতি যেমন, রৈখিক নির্ভরণ এবং সাধারণ লঘিষ্ট বর্গ নির্ভরণ হচ্ছে পরামিতিক, এই অর্থে যে, সেখানে নির্ভরণ ফাংশনকে কতগুলো অজানা পরামিতির মাধ্যমে সংজ্ঞায়িত করা হয়, যার মান প্রদত্ত উপাত্ত থেকে নির্ণয় করা হয়। অপরামিতিক নির্ভরণ বলতে ঐ পদ্ধতি বোঝায়, যা ফাংশনসমূহের একটি সুনির্দিষ্ট সেটের মধ্যে নির্ভরণ অপেক্ষককে থাকার অনুমতি দেয়, যেটি অসীম-মাত্রিকও হতে পারে।
নির্ভরণ বিশ্লেষণে ব্যবহৃত পদ্ধতিগুলোর কর্মক্ষমতা উপাত্ত-সৃষ্টি প্রক্রিয়ার রূপ, এবং তা কীভাবে নির্ভরণে ব্যবহৃত পদ্ধতিটির সাথে অন্বিত তার উপর নির্ভর করে। যেহেতু উপাত্ত-সৃষ্টি প্রক্রিয়ার প্রকৃত রূপ সাধারণত জানা থাকে না, নির্ভরণ বিশ্লেষণে অনেক সময় এই প্রক্রিয়া সম্বন্ধে অনুমিত স্বতঃসিদ্ধের ওপর কিছুটা নির্ভরশীল হতে হয়। এই স্বতঃসিদ্ধগুলো কখনও কখনও পরীক্ষণযোগ্য, যদি পর্যাপ্ত পরিমাণে উপাত্ত বিদ্যমান থাকে। পূর্বাভাসের জন্য নির্ভরণ প্রতিমানসমূহ অনেক সময়ই কার্যকরী, এমনকি যখন তা স্বতঃসিদ্ধগুলোকে পরিমিতভাবে লঙ্ঘন করে তখনও; যদিও তাদের কর্মক্ষমতা সন্তোষজনক না-ও হতে পারে। তা স্বত্বেও, অনেক ক্ষেত্রেই, বিশেষ করে পর্যবেক্ষণলব্ধ উপাত্তের ভিত্তিতে প্রভাব নগণ্য হলে বা কার্যকারণ-সম্পর্ক নিয়ে প্রশ্ন থাকলে, নির্ভরণ পদ্ধতি বিভ্রান্তিকর ফলাফল দিতে পারে।[২][৩]
সংকীর্ণ দৃষ্টিতে দেখলে, নির্ভরণ সুনির্দিষ্টভাবে কোন অবিচ্ছিন্ন প্রতিক্রিয়া (অধীন) চলকসমূহের নির্ণয় প্রক্রিয়াকে বোঝাতে পারে, যা শ্রেণিবিন্যাস প্রক্রিয়ায় ব্যবহৃত বিচ্ছিন্ন প্রতিক্রিয়া চলক নির্ণয়ের বিপরীত।[৪] অবিচ্ছিন্ন অধীন চলকের ক্ষেত্রে প্রক্রিয়াটিকে প্রাসঙ্গিক অন্যান্য সমস্যাগুলো থেকে আলাদা করার জন্য মেট্রিক নির্ভরণ নামে সুনির্দিষ্টভাবে অভিহিত করা যেতে পারে।[৫]
| যান্ত্রিক শিখন এবং উপাত্ত খনন |
|---|
 |
ইতিহাস[সম্পাদনা]
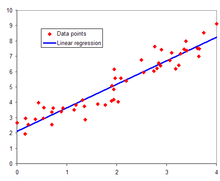
নির্ভরণের সবচেয়ে প্রাচীনতম রূপ ছিল লঘিষ্ঠ বর্গ পদ্ধতি, যেটি ১৮০৫ সালে লেজাঁদ্রে (Legendre)[৬], এবং ১৮০৯ সালে গাউস কর্তৃক প্রকাশিত হয়।[৭] লেজাঁদ্রে ও গাউস উভয়ই, জ্যোতির্বৈজ্ঞানিক পর্যবেক্ষণ থেকে, সূর্যের চারপাশের বস্তুসমূহের কক্ষপথ (অধিকাংশই ধূমকেতু, কিন্তু পরবর্তীকালে ঐ সময়ে নতুন আবিষ্কৃত কিছু ক্ষুদ্র গ্রহও ছিল) নির্ণয়ের সমস্যার ক্ষেত্রে এই পদ্ধতি প্রয়োগ করেছিলেন। ১৮২১ সালে গাউস এই লঘিষ্ঠ বর্গ তত্ত্বের আরও উন্নত রূপ প্রকাশ করেন[৮], যার মধ্যে গাউস-মার্কভ তত্ত্বের একটি রূপও অন্তর্ভুক্ত ছিল।
১৯শ শতকে একটি জৈবিক ঘটনার বর্ণনা করতে “নির্ভরণ” শব্দটি প্রথম প্রবর্তন করেন ফ্রান্সিস গল্টন (Francis Galton)। ঘটনাটি ছিল যে, দীর্ঘকায় পূর্বপুরুষ থেকে তাদের উত্তসূরিদের দৈর্ঘ্য ক্রমশ হ্রাস পেয়ে সাধারণ গড়পরতা মানের দিকে ধাবিত হতে থাকে (এ ঘটনা গড়ের দিকবর্তী নির্ভরণ নামেও পরিচিত)।[৯][১০] গল্টনের কাছে নির্ভরণের শুধুমাত্র জীববৈজ্ঞানিক অর্থই ছিল[১১][১২], কিন্তু পরবর্তীকালে উডনি ইউল এবং কার্ল পিয়ারসন তার কাজকে পরিসংখ্যানগত প্রেক্ষাপট হতে আরও সাধারণভাবে বিস্তৃত করেন।[১৩][১৪] ইউল ও পিয়ারসনের কাজে, প্রতিক্রিয়া ও ব্যাখ্যামূলক চলকের যুগ্ম-বণ্টন গাউসীয় বলে ধরা হয়। এই স্বতঃসিদ্ধটি রোনাল্ড ফিশারের এর ১৯২২ ও ১৯২৫ এর কাজের প্রেক্ষিতে দুর্বল হয়ে যায়।[১৫][১৬][১৭] ফিশার ধরে নেন যে, প্রতিক্রিয়া চলকের শর্তাধীন-বণ্টন গাউসীয় প্রকৃতির, কিন্তু যুগ্ম-বণ্টন তেমন নাও হতে পারে। এদিক থেকে ফিশারের অনুমান, ১৮২১ সালে প্রকাশিত গাউসের সূত্রায়নের কাছাকাছি।
বিংশ শতকের পঞ্চাশ ও ষাটের দশকের দিকে, অর্থনীতিবীদগণ নির্ভরণ গণনার জন্য তড়িৎ-যান্ত্রিক (electro-mechanical) ডেস্ক “ক্যালকুলেটর” ব্যবহার করতেন। ১৯৭০ এর আগে, একটি নির্ভরণের ফলাফল পাওয়ার জন্য কখনো কখনো ২৪ ঘণ্টা পর্যন্ত সময় লাগতো।[১৮]
নির্ভরণ পদ্ধতি এখনো সক্রিয় গবেষণার একটি ক্ষেত্র। সাম্প্রতিক দশকগুলোতে, বলিষ্ঠ নির্ভরণের (robust regression) জন্য নতুন পদ্ধতির বিকাশ ঘটেছে- যে সব নির্ভরণে পরস্পর অন্বিত প্রতিক্রিয়া যেমন, সময় ধারা ও ক্রমবৃদ্ধির বক্ররেখা অন্তর্ভুক্ত থাকে, যে নির্ভরণে সূচক (স্বাধীন চলক) বা প্রতিক্রিয়া চলকসমূহ হচ্ছে বক্ররেখা, চিত্র, লেখচিত্র, অথবা অন্য কোন জটিল উপাত্ত বস্তু, যে নির্ভরণ পদ্ধতিতে বিভিন্ন ধরনের উপাত্ত উপস্থিত থাকে না, অপরামিতিক নির্ভরণ, বেইজীয় নির্ভরণ পদ্ধতি, যে সব নির্ভরণে সূচক-চলকের পরিমাপে ত্রুটি থাকে, যে সব নির্ভরণে পর্যবেক্ষণের তুলনায় সূচক-চলকের সংখ্যা বেশি, এবং যে সব নির্ভরণের সাথে কার্যকারণ সম্পর্ক থাকে।
নির্ভরণ মডেলসমূহ[সম্পাদনা]
নির্ভরণ মডেলসমূহে নিম্নোক্ত পরামিতি ও চলকসমূহ অন্তর্ভুক্ত থাকে:
- অজ্ঞাত পরামিতি, যা দ্বারা সূচিত হয়, এবং কোন অদিক অথবা সদিক রাশিকে নির্দেশ করতে পারে।
- স্বাধীন চলক,
- অধীন চলক,
বিভিন্ন প্রায়োগিক ক্ষেত্রে, স্বাধীন ও অধীন চলকের স্থলে ভিন্ন ভিন্ন পরিভাষা ব্যবহৃত হয়ে থাকে।
কোন নির্ভরণ মডেল -কে কোন ফাংশন এবং এর সাথে অন্বিত করে।
।
একে প্রচলিত রীতিতে লেখা হয় হিসেবে। রিগেশন বিশ্লেষণ করার জন্য, ফাংশন এর আকার অবশ্যই সুনির্দিষ্ট হতে হয়। কখনো কখনো এবং এর মধ্যে বিদ্যমান সম্পর্ক সংক্রান্ত তথ্য, যা উপাত্তের ওপর নির্ভরশীল নয়, তার ভিত্তিতে এই ফাংশনের আকার নির্ধারিত হয়। যদি এমন কোন তথ্য জানা না থাকে, এর নমনীয় বা সুবিধাজনক কোন আকার নির্বাচন করা হয়।
ধরা যাক, অজ্ঞাত পরামিতি এর ভেক্টরের দৈর্ঘ্য । নির্ভরণ বিশ্লেষণ করার জন্য ব্যবহারকারীকে অবশ্যই অধীন চলক সম্পর্কে তথ্য সরবরাহ করতে হবে:
- যদি আকারের -সংখ্যক উপাত্ত বিন্দু থাকে, যেখানে নির্ভরণ বিশ্লেষণের সবচেয়ে উৎকৃষ্ট পদ্ধতিগুলো সেখানে প্রয়োগ করা যায় না: কেননা, যে সমীকরণ জোট দ্বারা নির্ভরণ মডেলটি সংজ্ঞায়িত হয় তা অনির্ণেয়, এবং এর মান নির্ণয়ের জন্য পর্যাপ্ত উপাত্ত বিন্দু থাকে না। .
- যদি ঠিক সংখ্যক উপাত্ত বিন্দু পাওয়া যায়, এবং ফাংশন রৈখিক প্রকৃতির হয়, সমীকরণ এর সমাধানের আসন্ন মানের পরিবর্তে নির্ভুল মান পাওয়া যায়। এতে নির্ভরণটি হ্রাস পেয়ে -সংখ্যক অজ্ঞাত রাশি ( এর উপাদানসমূহ) বিশিষ্ট -সংখ্যক সমীকরণের সমাধানে পরিণত হয়, রৈখিকভাবে স্বাধীন হলে যার একটি অনন্য সমাধান থাকে। যদি অরৈখিক হয়, তাহলে সমাধান না-ও থাকতে পারে, অথবা অসংখ্য সমাধানও থাকতে পারে।
- সবচেয়ে গতানুগতিক ক্ষেত্র হচ্ছে যেখানে সংখ্যক উপাত্ত বিন্দু পাওয়া যায়। এক্ষেত্রে উপাত্তের সাথে সঙ্গতিপূর্ণ, এর অনন্য একটি মান অনুমানের জন্য যথেষ্ট সংখ্যক তথ্য, উপাত্তের মধ্যে বিদ্যমান থাকে, এবং ঐ উপাত্তে নির্ভরণ মডেল প্রয়োগ করা হলে তাকে এর একটি অতি-নির্ণীত জোট হিসেবে বিবেচনা করা যায়। .
সর্বশেষ ক্ষেত্রটিতে, নির্ভরণ বিশ্লেষণ নিম্নোক্ত পন্থাগুলো প্রদান করে:
- অজ্ঞাত পরামিতি এর একটি সমাধান নির্ণয় যা, উদাহরণস্বরূপ, অধীন চলক এর প্রাপ্ত মান ও অনুমিত মানের মধ্যে পার্থক্য হ্রাস করে (লঘিষ্ঠ বর্গ পদ্ধতি নামেও পরিচিত)।
- সুনির্দিষ্ট পরিসংখ্যানগত অনুমানের ওপর নির্ভর করে, নির্ভরণ বিশ্লেষণ উদ্বৃত্ত তথ্য ব্যবহার করে অজ্ঞাত পরামিতি এবং অধীন চলক এর অনুমিত মানগুলো সম্পর্কে পরিসংখ্যানগত তথ্য সরবরাহ করে।
স্বাধীন পরিমাপের আবশ্যকীয় সংখ্যা[সম্পাদনা]
কোন নির্ভরণ মডেল বিবেচনা করা যাক, যার তিনটি অজ্ঞাত পরামিতি রয়েছে। ধরা যাক, কোন পরীক্ষক স্বাধীন চলক ভেক্টর (যার মধ্যে স্বাধীন চলক অন্তর্ভুক্ত) এর ঠিক একই মানের জন্য ১০টি পাঠ নেন। এক্ষেত্রে, নির্ভরণ বিশ্লেষণ তিনটি অজ্ঞাত পরামিতির জন্য প্রাক্কলিত অনন্য মানের সেট নির্ণয়ে ব্যর্থ হয়; কেননা পরীক্ষক পর্যাপ্ত তথ্য প্রদান করেননি। এখান থেকে বড়জোর গড় মান এবং অধীন চলক এর আদর্শ বিচ্যুতি অনুমান করা যেতে পারে। একইভাবে, এর দুটি ভিন্ন মানের জন্য পাঠ নিলে তা দুটি অজানা রাশির নির্ভরণের জন্য পর্যাপ্ত তথ্য সরবরাহ করতো, কিন্তু তিন বা তার বেশি অজ্ঞাত রাশির জন্য নয়।
যদি পরীক্ষক স্বাধীন চলক ভেক্টর এর তিনটি ভিন্ন ভিন্ন মানের জন্য পাঠ নিতেন, তাহলে নির্ভরণ বিশ্লেষণ থেকে এর তিনটি অজানা পরামিতির অনন্য প্রাক্কলিত মানের সেট পাওয়া যেত।
সাধারণ রৈখিক নির্ভরণের ক্ষেত্রে, ওপরের উক্তিটি, ম্যাট্রিক্স বিপরীতযোগ্য - এই শর্তের সমতুল্য।
যখন গৃহীত পাঠ সংখ্যা অজ্ঞাত পরামিতি অপেক্ষা বৃহত্তর, এবং পাঠ-ত্রুটি স্বাভাবিকভাবে বণ্টিত থাকে, তখন -তে বিদ্যমান উদ্বৃত্ত তথ্য, অজ্ঞাত পরামিতি সম্পর্কে পরিসংখ্যানগত পূর্বানুমান করতে ব্যবহৃত হয়। এই উদ্বৃত্ত তথ্যকে নির্ভরণের স্বাধীনতার মাত্রা বলা হয়।
মৌলিক স্বতঃসিদ্ধসমূহ[সম্পাদনা]
নির্ভরণ বিশ্লেষণের ক্ষেত্রে গুরুত্বপূর্ণ কিছু স্বতঃসিদ্ধের মধ্যে রয়েছে:
- অনুমানভিত্তিক পূর্বাভাস প্রদানের জন্য, নমুনাটিকে সমগ্র ক্ষেত্রের প্রতিনিধিত্বমূলক হতে হবে।
- ত্রুটি হচ্ছে একটি যথেচ্ছ চলক, ব্যাখ্যামূলক চলকসমূহের শর্তসাপেক্ষে যার গড় শূন্য।
- কোন ত্রুটি ছাড়াই স্বাধীন চলকসমূহ পরিমাপ করা হয় (উল্লেখ্য যে, যদি তেমনটা না হয়, চলকীয় ত্রুটি মডেল ব্যবহার করে মডেল গঠন করা যায়)।
- স্বাধীন চলকসমূহ (predictor বা সূচক) রৈখিকভাবে স্বাধীন, অর্থাৎ, কোন একটি সূচকীয় চলককে অবশিষ্ট চলকসমূহের রৈখিক বিন্যাস দ্বারা প্রকাশ করা যায় না।
- ত্রুটিসমূহ পরস্পর সম্পর্কহীন, তার মানে, ত্রুটিসমূহের ভেদাংক-সহভেদাংক ম্যাট্রিক্স (variance-covariance matrix) একটি কর্ণ ম্যাট্রিক্স, এবং প্রতিটি অশূন্য উপাদান ঐ ত্রুটির একটি ভেদাংক (variance)।
- সমগ্র পর্যবেক্ষণজুড়েই ত্রুটির ভেদাংক ধ্রুব থাকে (সমভেদাঙ্কত্ব বা homoscedasticity)। যদি তা না হয়, তাহলে এর পরিবর্তে ভরযুক্ত লঘিষ্ঠ বর্গ পদ্ধতি বা অন্য কোন পদ্ধতি ব্যবহৃত হতে পারে।
এগুলোই লঘিষ্ঠ-বর্গ প্রাক্কলক (least-squares estimator) কর্তৃক আকাংক্ষিত বৈশিষ্ট্যাবলি অর্জনের জন্য পর্যাপ্ত শর্ত; বিশেষ করে, এই স্বতঃসিদ্ধগুলো ইঙ্গিত করে যে, রৈখিক নিরপেক্ষ প্রাক্কলক শ্রেণিতে এই নির্ণীত পরামিতিগুলো পক্ষপাতহীন, সঙ্গতিপূর্ণ, এবং কার্যকর হবে। এটা বলে রাখাটা গুরুত্বপূর্ণ যে, অনুমানের সাথে সন্তোষজনক প্রকৃত উপাত্ত পাওয়া বেশ বিরল। কখনো কখনো অনুমান থেকে পার্থক্য কতটুকু- তা থেকে, মডেলটি ব্যবহারযোগ্যতা থেকে কতখানি দূরে আছে তা পরিমাপ করা হয়। আরও উন্নত প্রক্রিয়া অবলম্বন করে এসব স্বতঃসিদ্ধ শিথিল করা যেতে পারে। পরিসংখ্যানগত বিশ্লেষণের প্রতিবেদনে সচরাচর নমুনা উপাত্তের ওপর পরীক্ষা-নিরীক্ষার বিশ্লেষণ ও মডেলটির প্রণালিগত যথার্থতা এবং মডেলটির ব্যবহারযোগ্যতার উল্লেখ করা হয়।
স্বাধীন ও অধীন চলকসমূহ প্রায়শই বিন্দু অবস্থানে পরিমাপকৃত মান নির্দেশ করে। যেসব চলক পরিসংখ্যানগত স্বতঃসিদ্ধগুলো লঙ্ঘন করে, তাদের মধ্যে স্থানগত-প্রবণতা (spatial trends) এবং স্থানগত স্বয়ংক্রিয়-সংশ্লিষ্টতা (spatial auto-correlation) বিদ্যমান থাকতে পারে। এ ধরনের উপাত্তের জন্য ব্যবহৃত একটি পদ্ধতি হচ্ছে ভৌগোলিক ভরযুক্ত নির্ভরণ।[১৯] এছাড়া, চলকের মানে ক্ষেত্রফল দ্বারা সমষ্টিকৃত মানও অন্তর্ভুক্ত থাকতে পারে। সমষ্টিকৃত উপাত্ত থেকে সৃষ্ট সংশোধনযোগ্য ক্ষেত্রফল সমস্যা (modifiable areal unit problem) নির্ভরণের পরামিতিতে চরম পার্থক্যের কারণ হতে পারে।[২০] যখন রাজনৈতিক সীমা, ডাক কোড বা আদমশুমারি এলাকার ভিত্তিতে উপাত্ত বিশ্লেষণ করা হয়, ভিন্ন ভিন্ন এককের জন্য প্রাপ্ত ফলাফল স্পষ্টভাবেই ভিন্ন হতে পারে।
রৈখিক নির্ভরণ[সম্পাদনা]
রৈখিক নির্ভরণে, কোন মডেলের শনাক্তকরণ-বিবরণীতে বলা হয় যে, অধীন চলক হচ্ছে পরামিতি সমূহের একটি রৈখিক সমাবেশ (কিন্তু স্বাধীন চলক এর ক্ষেত্রে তা রৈখিক হওয়া আবশ্যক নয়)। উদাহরণস্বরূপ, সরল রৈখিক নির্ভরণে (simple linear regression) -সংখ্যক উপাত্ত বিন্দুর মডেল গঠনে একটি স্বাধীন চলক , দুটি পরামিতি ও বিদ্যমান থাকে:
সরলরেখা: ।
বহু-রৈখিক নির্ভরণে, বেশ কতগুলো স্বাধীন চলক বা স্বাধীন চলকের ফাংশন থাকে।
ওপরের নির্ভরণে পদটি যোগ করে পাওয়া যায়:
পরাবৃত্ত: ।
এটাও রৈখিক নির্ভরণ; যদিও ডানপক্ষের রাশিটিতে স্বাধীন চলক এর দ্বিঘাত রয়েছে, এটা পরামিতি এবং এর মধ্যে রৈখিক।
উভয় ক্ষেত্রেই, হচ্ছে ত্রুটিসূচক পদ এবং নিম্নলিপি দ্বারা কোন নির্দিষ্ট পর্যবেক্ষণ সূচিত হয়।
মনোযোগ পুনরায় সরলরৈখিক ক্ষেত্রের দিকে আনা যাক: ঘটনাজগৎ থেকে যথেচ্ছ একটি নমুনা নিলে, ঘটনাজগতের পরামিতিগুলো নির্ণয় করা হয় এবং নমুনা রৈখিক নির্ভরণ মডেল তৈরি করা হয়:
।
অবশেষ , হচ্ছে অধীন চলকের মডেল কর্তৃক অনুমিত মান , এবং প্রকৃত মান এর মধ্যকার ব্যবধান। এর একটি নির্ণয় পদ্ধতি হচ্ছে সাধারণ লঘিষ্ঠ বর্গ পদ্ধতি। এই পদ্ধতিতে অবশেষের বর্গের সমষ্টি, SSR (Sum of Squared Residuals) এর হ্রাসকরণের মাধ্যমে পরামিতির মান নির্ণয় করা হয়:
।
এই ফাংশনের লঘিষ্ঠকরণের ফলে কতগুলো অভিলম্ব সমীকরণের একটি জোট পাওয়া যায়, পরামিতিগুলোর যুগপৎ রৈখিক সমীকরণ জোট পাওয়া যায়, যেগুলো সমাধান করে পরামিতি প্রাক্কলক পাওয়া যায়।

সরল নির্ভরণের ক্ষেত্রে, লঘিষ্ঠ বর্গের সূত্রগুলো হচ্ছে-
,
যেখানে হচ্ছে এর গড় মান এবং হচ্ছে এর গড় মান।
জনসংখ্যা ত্রুটি'র (population error) ভেদাংক সর্বত্র ধ্রুব ধরে নিলে, ঐ ভেদাংকের মান পাওয়া যায়:
।
একে নির্ভরণের গড় বর্গ ত্রুটি (MSE: Mean Square Error) বলা হয়। হর হচ্ছে নমুনার আকার থেকে ঐ একই উপাত্তের মডেলের পরামিতি সংখ্যার অন্তর, -সংখ্যক প্রত্যাবর্তকের জন্য , আর ছেদক ব্যবহার করলে তা হবে ।[২১] এক্ষেত্রে, বলে হর হয়।
নির্ণীত পরামিতির প্রমিত ত্রুটি হচ্ছে-
,
।
আরও যদি ধরে নেওয়া হয় যে, জনসংখ্যা ত্রুটি অভিলম্বভাবে বণ্টিত, গবেষকবৃন্দ জনসংখ্যা পরামিতিগুলো সম্পর্কে এসব নির্ণীত প্রমিত ত্রুটিসমূহ ব্যবহার করে, আস্থা ব্যবধি (confidence intervals) তৈরি এবং প্রকল্প পরীক্ষণ (hypothesis tests) করে দেখতে পারেন।
সাধারণ রৈখিক মডেল[সম্পাদনা]
আরও সাধারণ বহু-নির্ভরণ মডেলের -সংখ্যক স্বাধীন চলক থাকে:
যেখানে হচ্ছে -তম স্বাধীন চলকে -তম পর্যবেক্ষণ। যদি প্রথম স্বাধীন চলকের মান সকল এর জন্য ১ হয়, , তাহলে কে বলা হয় নির্ভরণ ছেদক (regression intercept)।
লঘিষ্ঠ বর্গের পরামিতি নির্ণয় করা হয় -সংখ্যক অভিলম্ব সমীকরণ থেকে। এর অবশেষ লেখা যায় নিমোক্তভাবে:
।
অভিলম্ব সমীকরণ হচ্ছে-
।
ম্যাট্রিক্স চিহ্নলিপিতে, অভিলম্ব সমীকরণগুলো লেখা হয়-
যেখানে এর -তম উপাদানটি হচ্ছে , কলাম ভেক্টর এর -তম উপাদান হচ্ছে , এবং এর -তম উপাদান হচ্ছে । এজন্য, হচ্ছে , হচ্ছে , এবং হচ্ছে । সমাধানটি হলো,
।
যাচাইকরণ[সম্পাদনা]
একবার কোন নির্ভরণ মডেল তৈরি হয়ে গেলে, মডেলের উপযোগিতা (goodness of fit) এবং নির্ণীত পরামিতিসমূহের পরিসংখ্যানগত তাৎপর্য নিশ্চিত করা জরুরি। সাধারণত উপযোগিতা যাচাই করার জন্য R-এর বর্গ, অবশেষের বিন্যাস বিশ্লেষণ এবং প্রকল্প পরীক্ষণ অন্তর্ভুক্ত। পরিসংখ্যানগত তাৎপর্য সার্বিক উপযোগিতার F-অভীক্ষা (Fisher test) ও তারপর স্বতন্ত্র পরামিতিসমূহের t-অভীক্ষা’র মাধ্যমে যাচাই করা যায়।
এইসব শনাক্তকারী পরীক্ষার ব্যাখ্যা অনেকটাই নির্ভর করে মডেলটির অনুমিত স্বতঃসিদ্ধগুলোর ওপর। যদিও অবশেষ পরীক্ষণের মাধ্যমে কোন মডেলের বৈধতা বাতিল করে দেওয়া যায়, তবে t-অভীক্ষা ও F-অভীক্ষার ফলাফল কখনো কখনো ব্যাখ্যা করা বেশ কঠিন হয়ে যায় যদি মডেলটির স্বতঃসিদ্ধগুলো লংঘিত হয়। যেমন- যদি ত্রুটিসূচক পদটির অভিলম্ব বণ্টন না হয়ে থাকে, ক্ষুদ্র নমুনায় নির্ণীত পরামিতিগুলো অভিলম্ব বণ্টন অনুসরণ করবে না এবং এতে ঐ নমুনা থেকে কোন অনুমিতিক সিদ্ধান্ত নেওয়া জটিল হয়ে যায়। তবে তুলনামূলকভাবে বৃহৎ নমুনায়, কেন্দ্রীয় সীমা উপপাদ্য প্রয়োগ করা যায় যেন প্রকল্প পরীক্ষণে অসীমতট অনুমান করে অগ্রসর হওয়া যায়।
সীমাবদ্ধ অধীন চলক[সম্পাদনা]
অর্থমিতিতে প্রায়ই সীমাবদ্ধ অধীন চলক দেখা যায়, যেগুলো হচ্ছে প্রতিক্রিয়া চলক, যারা হয় শ্রেণিবদ্ধ চলক অথবা নির্দিষ্ট সীমাভুক্ত থাকতে বাধ্য এমন চলক।
প্রতিক্রিয়া চলক অবিচ্ছিন্ন-নয় (বাস্তব সংখ্যারেখার কোন উপসেটের মধ্যে “সীমাবদ্ধ” থাকে) এমন হতে পারে। দ্বিমিক (শূন্য অথবা এক) চলকের জন্য, যদি লঘিষ্ঠ-বর্গ রৈখিক নির্ভরণের মাধ্যমে বিশ্লেষণ করা হয়, ঐ মডেলকে বলা হয় রৈখিক সম্ভাব্যতা মডেল। দ্বিমিক অধীন চলকের অরৈখিক মডেলের মধ্যে রয়েছে প্রোবিট (probit) এবং লজিট মডেল (logit model)। বহুচলকীয় প্রোবিট মডেল হচ্ছে, বেশ কতগুলো দ্বিমিক অধীন চলক ও কিছু স্বাধীন চলকের মধ্যে বিদ্যমান যুগ্ম সম্পর্ক নির্ণয়ের একটি প্রমিত পদ্ধতি। দুই এর অধিক মানবিশিষ্ট শ্রেণিবদ্ধ চলকের জন্য বহুপদী লজিট রয়েছে। দুই এর অধিক মানবিশিষ্ট ক্রমবাচক চলকের জন্য রয়েছে ক্রমবদ্ধ লজিট (ordered logit) এবং ক্রমবদ্ধ প্রোবিট (ordered probit) মডেল। যখন অধীন চলক কেবল মাঝে মাঝে পরিলক্ষিত হয়, তখন নিরীক্ষামূলক নির্ভরণ মডেল, এবং আলোচ্য ঘটনাজগৎ থেকে নমুনাটি যথেচ্ছভাবে নির্বাচিত না হয়ে থাকলে হেকম্যান সংশোধন ব্যবহৃত হয়। এই পদ্ধতির একটি বিকল্প হচ্ছে শ্রেণিবদ্ধ চলকসমূহের মধ্যে পলি-কোরিক বা পলি-সিরিয়াল সামঞ্জস্য (polychoric বা polyserial correlations) এর ওপর ভিত্তি করে গঠিত রৈখিক নির্ভরণ। এই পদ্ধতিগুলোর পার্থক্য দেখা যায় ঘটনাজগতে চলকসমূহের বণ্টন-সংক্রান্ত স্বতঃসিদ্ধ অনুমানের ক্ষেত্রে। যদি কোন চলক ধনাত্মক ক্ষুদ্র মানবিশিষ্ট হয় এবং কোন ঘটনার পুনরাবৃত্তির প্রতিনিধিত্ব করে, পয়সোঁ নির্ভরণ অথবা ঋণাত্মক দ্বিপদী মডেলের মতন গণনা মডেল ব্যবহার করা যেতে পারে।
অরৈখিক নির্ভরণ[সম্পাদনা]
যখন কোন মডেলের পরামিতির ফাংশনগুলো রৈখিক না হয়, কোন একটি পুনরাবৃত্তিমূলক পদ্ধতি অবলম্বন করে এর বর্গের সমষ্টি লঘিষ্ঠ করতে হয়। এর ফলে অনেক জটিলতার সৃষ্টি হয় যা রৈখিক ও অরৈখিক লঘিষ্ঠ বর্গের মধ্যে পার্থক্য -তে বর্ণিত আছে।
অন্তর্পাতন এবং বহির্পাতন[সম্পাদনা]

নির্ভরণ মডেলসমূহ X-চলকসমূহের প্রদত্ত জানা মানের জন্য Y-চলকের মান গণনা করে। কোন মডেলে সঙ্গতিপূর্ণভাবে ব্যবহারের জন্য, এর উপাত্ত সেটের অন্তর্বর্তী মানের ব্যবধি থেকে কোন মান অনুমান করার প্রক্রিয়াকে অনানুষ্ঠানিকভাবে অন্তর্পাতন (interpolation) বলে। আর উপাত্ত সেটের ব্যাপ্তির বাইরে কোন অনুমানকে বলা হয় বহির্পাতন (extrapolation)। বহির্পাতন প্রক্রিয়া নির্ভরণের স্বতঃসিদ্ধের ওপর অনেকখানি নির্ভরশীল। উপাত্তের যতখানি বাইরে বহির্পাতন করা হয়, অনুমিত এবং নমুনা উপাত্ত বা প্রকৃত মানের মধ্যে পার্থক্যের কারণে, কোন মডেলের ব্যর্থ হওয়ার সম্ভাবনা ততই বেড়ে যায়।
বহির্পাতনের ক্ষেত্রে সাধারণ নির্দেশনা হচ্ছে[তথ্যসূত্র প্রয়োজন], অধীন চলকের অনুমিত মানের সাথে একটি অনুমান ব্যবধিও উল্লেখ করতে হয় যেন তা অনুমানের অনিশ্চয়তা নির্দেশ করে। স্বাধীন চলকের (গুলোর) মান যদি পর্যবেক্ষণ উপাত্তের বাইরে চলে যায়, এ ধরনের ব্যবধির ব্যাপ্তি দ্রুত হারে বর্ধিত হয়।
এসব ও অন্যান্য কিছু কারণে, অনেকেই বহির্পাতন করাটা সমীচীন নয় বলে মনে করেন।[২৩]
তবে এর মধ্যেই যে সম্ভাব্য সকল মডেলিং ত্রুটিঅন্তর্ভুক্ত, তা নয়: বিশেষ করে, Y এবং X এর মধ্যে সম্পর্ক নির্ণয়ে সুনির্দিষ্ট আকার অনুমান করা। একটি যথাযথ নির্ভরণ বিশ্লেষণে, পরিলক্ষিত উপাত্তের সাথে অনুমিত আকারের সামঞ্জস্যের মূল্যায়ন অন্তর্ভুক্ত থাকে, কিন্তু তা শুধুমাত্র স্বাধীন চলকের প্রদত্ত মানের ব্যাপ্তির মধ্যেই করা সম্ভব। এর মানে হচ্ছে, কোন বহির্পাতন প্রক্রিয়া নির্ভরণ সম্পর্কের কাঠামোগত আকার সম্পর্কিত অনুমানের ওপর বিশেষভাবে নির্ভরশীল। এক্ষেত্রে সর্বোত্তম পরামর্শ হচ্ছে[তথ্যসূত্র প্রয়োজন], শুধুমাত্র হিসাবের সুবিধার জন্য চলক ও পরামিতি- উভয় ক্ষেত্রেই রৈখিক, এমন সম্পর্ক অনুমান করে নেওয়া উচিৎ নয়, বরং জানা সকল তথ্য ব্যবহার করে নির্ভরণ মডেল গঠন করা উচিৎ। যদি এমনটা জানা থাকে যে, অধীন চলকের মান একটি নির্দিষ্ট সীমার বাইরে যেতে পারবে না, তাহলে সেই অনুসারে মডেল নির্বাচন করা সমীচীন- এমনকি যদি পর্যবেক্ষণ উপাত্ত সেটের কোন মানই ঐ সীমার নিকটবর্তী না হয়। বহির্পাতন বিবেচনা করলে, নির্ভরণের জন্য একটি যথার্থ কার্যকর আকার বাছাই করার ধাপটির তাৎপর্য অনেক। কম করে হলেও, এটা নিশ্চিত করে যে কোন মডেল থেকে প্রাপ্ত বহির্পাতন "বাস্তবসম্মত" (অথবা জ্ঞাত রাশির সাথে সঙ্গতিপূর্ণ)।
শক্তি এবং নমুনার আকার গণনা[সম্পাদনা]
কোন মডেলে পর্যবেক্ষণ সংখ্যা বনাম স্বাধীন চলকের সংখ্যার মধ্যে সম্পর্ক স্থাপনের জন্য সম্মত কোন সাধারণ পদ্ধতি নেই। গুড এবং হার্ডিন কর্তৃক প্রস্তাবিত একটি প্রচলিত রীতি হচ্ছে , যেখানে হচ্ছে নমুনার আকার, হচ্ছে স্বাধীন চলকের সংখ্যা, এবং হচ্ছে অভীষ্ট নির্ভুল মাত্রা অর্জনের জন্য আবশ্যক পর্যবেক্ষণ সংখ্যা, যদি ঐ মডেলে কেবল একটি স্বাধীন চলক থাকতো।[২৪] যেমন- কোন গবেষক একটি রৈখিক নির্ভরণ মডেল গঠন করছেন যার উপাত্ত সেট হচ্ছে ১০০০ জন রোগী ()। যদি ঐ গবেষক সিদ্ধান্ত নেন যে, নির্ভুলভাবে একটি সরলরেখা কে সংজ্ঞায়িত করতে পাঁচটি পর্যবেক্ষণ প্রয়োজন, তাহলে ঐ মডেল কর্তৃক ধারণকৃত স্বাধীন চলকের সর্বোচ্চ সংখ্যা হবে ৪, কেননা
।
অন্যান্য পদ্ধতি[সম্পাদনা]
যদিও কোন নির্ভরণ মডেলের পরামিতিসমূহ সচরাচরভাবে লঘিষ্ঠ বর্গ পদ্ধতিতে নির্ণয় করা হয়, অন্যান্য পদ্ধতিও ব্যবহৃত হয়েছে, যার মধ্যে রয়েছে:
- বেইজীয় পদ্ধতি, যেমন- বেইজীয় রৈখিক নির্ভরণ
- শতকরা নির্ভরণ, যেসব ক্ষেত্রে শতকরা ত্রুটি হ্রাস করা অধিকতর উপযুক্ত।[২৫]
- লঘিষ্ঠ পরম বিচ্যুতি, চরম বিচ্যুতির ক্ষেত্রে যা অধিক বলিষ্ঠ, এবং সমাংশক নির্ভরণের (quantile regression) দিকে ধাবিত করে।
- অপরামিতিক নির্ভরণ, পর্যবেক্ষণের সংখ্যা অনেক বেশি হতে হয়, এবং গণনাগতভাবে শ্রমসাধ্য।
- দৃশ্যকল্প উন্নয়ন (Scenario Optimization), যা ব্যবধি অনুমানকারী মডেল (Interval Predictor Models) এর দিকে ধাবিত হয়।
- দূরত্ব পরিমাপ শিক্ষণ, যা কোন প্রদত্ত স্থানের জন্য অর্থবহ একটি দূরত্ব অনুসন্ধানের মাধ্যমে জানা যায়।[২৬]
সফটওয়্যার[সম্পাদনা]
আরও বিস্তারিত তালিকার জন্য, পরিসংখ্যান-সংক্রান্ত প্যাকেজের তালিকা দেখুন।
সকল পরিসংখ্যান সফটওয়্যার প্যাকেজেই লঘিষ্ঠ বর্গ বিশ্লেষণ ও অনুমিতিক গণনা করা যায়। কোন স্প্রেডশীট অ্যাপলিকেশন ও ক্যালকুলেটর দ্বারা, লঘিষ্ঠ বর্গ ব্যবহার করে সরল রৈখিক নির্ভরণ এবং বহু-রৈখিক নির্ভরণ করা যায়। যদিও অনেক পরিসংখ্যান প্যাকেজেই অপরামিতিক এবং বলিষ্ঠ নির্ভরণ করা যায়, এই পদ্ধতিগুলো তুলনামূলকভাবে কম প্রমিত; বিভিন্ন সফটওয়্যার প্যাকেজে বিভিন্ন পদ্ধতি ব্যবহৃত হয়ে থাকে, এবং একই নামের পদ্ধতি ভিন্ন ভিন্ন প্যাকেজে ভিন্ন ভিন্ন উপায়ে প্রয়োগ করা যেতে পারে। জরিপ বিশ্লেষণ ও স্নায়বিক-ইমেজিং এর মত ক্ষেত্রে ব্যবহারের জন্য, বিশেষায়িত নির্ভরণ সফটওয়্যার এর বিকাশ ঘটেছে।
আরও দেখুন[সম্পাদনা]
- উপযুক্ত বক্ররেখা গঠন
- প্রাক্কলন তত্ত্ব
- পূর্বাভাস
- ভেদাংকের ব্যাখ্যাতীত ভগ্নাংশ
- ফাংশন প্রাক্কলন
- সাধারণিকৃত রৈখিক মডেল
- ক্রিগিং (একটি রৈখিক লঘিষ্ঠ বর্গ অনুমান অ্যালগরিদম)
- স্থানিক নির্ভরণ
- সংশোধনযোগ্য ক্ষেত্রফল সমস্যা
- বহুচলকীয় অভিযোজিত নির্ভরণ স্প্লাইন
- বহুচলকীয় অভিলম্ব বণ্টন
- পিয়ারসনের প্রোডাক্ট-মোমেন্ট সামঞ্জস্য গুণক
- আপাত-ভেদাংক
- অনুমান ব্যবধি
- নির্ভরণের বৈধতা যাচাইকরণ
- বলিষ্ঠ নির্ভরণ
- খণ্ডায়িত নির্ভরণ
- সংকেত প্রক্রিয়াকরণ
- ধাপভিত্তিক নির্ভরণ
- ঝোঁক পূর্বানুমান
তথ্যসূত্র[সম্পাদনা]
- ↑ "Necessary Condition Analysis - Erasmus Research Institute of Management - ERIM"। www.erim.eur.nl। সংগ্রহের তারিখ ২০১৯-০৭-২৬।
- ↑ Freedman, David A. (২০০৯-০৪-২৭)। Statistical Models: Theory and Practice (ইংরেজি ভাষায়)। Cambridge University Press। আইএসবিএন 9781139477314।
- ↑ Cook, R. Dennis; Weisberg, Sanford (১৯৮২)। "Criticism and Influence Analysis in Regression"। Sociological Methodology। 13: 313–361। আইএসএসএন 0081-1750। ডিওআই:10.2307/270724।
- ↑ Bishop, Christopher M. (২০০৬)। Pattern Recognition and Machine Learning। Springer। পৃষ্ঠা ৩। আইএসবিএন 0387310738।
- ↑ "Ordinal regression"। Wikipedia (ইংরেজি ভাষায়)। ২০১৯-০৩-০২।
- ↑ Legendre, Adrien Marie (১৮০৫)। Nouvelles méthodes pour la détermination des orbites des comètes (ফরাসি ভাষায়)। F. Didot।
- ↑ C.F. Gauss. Theoria Motus Corporum Coelestium in Sectionibus Conicis Solem Ambientum. (1809)
- ↑ Gauss, Carl Friedrich (১৮২৩)। Theoria combinationis observationum erroribus minimis obnoxiae (লাতিন ভাষায়)। H. Dieterich।
- ↑ Mogull, Robert G. (২০০৪)। Second-Semester Applied Statistics। Kendall/Hunt Publishing Company। পৃষ্ঠা ৫৯। আইএসবিএন 978-0-7575-1181-3।
- ↑ Galton, Francis (মে ১৯৮৯)। "Kinship and Correlation"। Statistical Science (ইংরেজি ভাষায়)। 4 (2): 81–86। আইএসএসএন 0883-4237। ডিওআই:10.1214/ss/1177012581।
- ↑ Francis Galton। "Typical laws of heredity", Nature ১৫ (১৮৭৭), ৪৯২-৪৯৫, ৫১২-৫১৪, ৫৩২-৫৩৩। (গল্টন এই সাময়িকীতে "reversion" শব্দটি ব্যবহার করেন, যা মটরশুঁটির আকার নিয়ে আলোচনা করে।)
- ↑ Francis Galton। Presidential address, Section H, Anthropology. (১৮৮৫) (গল্টন এই সাময়িকীতে "regression" শবটি ব্যবহার করেন, যা মানুষের উচ্চতা নিয়ে আলোচনা করে।)
- ↑ Yule, G. Udny (১৮৯৭-১২-০১)। "On the Theory of Correlation"। ডিওআই:10.2307/2979746।
- ↑ Pearson, Karl (১৯০৩-০১-০১)। "The Law of Ancestral Heredity"। ডিওআই:10.1093/biomet/2.2.211।
- ↑ "The Goodness of Fit of Regression Formulae and the Distribution of Regression Coefficients"। Proceedings of the National Academy of Sciences of the United States of America। 12 (12): 773। ডিসেম্বর ১৯২৬। আইএসএসএন 0027-8424। পিএমসি 1084801
 ।
।
- ↑ "Classics in the History of Psychology -- Fisher (1925) Index"। psychclassics.yorku.ca। সংগ্রহের তারিখ ২০১৯-০৭-২৬।
- ↑ Aldrich, John (নভেম্বর ২০০৫)। "Fisher and Regression"। Statistical Science (ইংরেজি ভাষায়)। 20 (4): 401–417। আইএসএসএন 0883-4237। ডিওআই:10.1214/088342305000000331।
- ↑ "Finance and Development"। Finance and Development | F&D (ইংরেজি ভাষায়)। সংগ্রহের তারিখ ২০১৯-০৭-২৬।
- ↑ Fotheringham, A. Stewart. (২০০২)। Geographically weighted regression : the analysis of spatially varying relationships। Brunsdon, Chris., Charlton, Martin.। Chichester, West Sussex: Wiley। আইএসবিএন 0470855258। ওসিএলসি 51520402।
- ↑ Fotheringham, A S; Wong, D W S (জুলাই ১৯৯১)। "The Modifiable Areal Unit Problem in Multivariate Statistical Analysis"। Environment and Planning A: Economy and Space (ইংরেজি ভাষায়)। ২৩ (৭): ১০২৫–১০৪৪। আইএসএসএন 0308-518X। ডিওআই:10.1068/a231025। সংগ্রহের তারিখ ২৯ আগস্ট ২০১৯।
- ↑ Steel, R.G.D.; Torrie, J.H. (১৯৬০)। Principles and Procedures of Statistics with Special Reference to the Biological Sciences। McGraw Hill। পৃষ্ঠা ২৮৮।
- ↑ Rouau; Mathieu (২০১৩)। Probability, Statistics and Estimation। পৃষ্ঠা ৬০।
- ↑ Chiang, Chin Long, 1915-2014. (২০০৩)। Statistical methods of analysis। River Edge, N.J.: World Scientific। আইএসবিএন 9812383093। ওসিএলসি 53877749।
- ↑ Good, Phillip I. (২০০৯)। Common errors in statistics (and how to avoid them)। Hardin, James W. (James William) (3rd ed সংস্করণ)। Hoboken, N.J.: Wiley। আইএসবিএন 9780470457986। ওসিএলসি 264671141।
- ↑ Tofallis, Chris (২০০৯)। "Least Squares Percentage Regression"। SSRN Electronic Journal (ইংরেজি ভাষায়)। আইএসএসএন 1556-5068। ডিওআই:10.2139/ssrn.1406472।
- ↑ YangJing Long (২০০৯)। "Human age estimation by metric learning for regression problems"। Proc. International Conference on Computer Analysis of Images and Patterns: পৃষ্ঠা ৭৪-৮২।
আরও পড়ুন[সম্পাদনা]
- William H. Kruskal and Judith M. Tanur, ed. (১৯৭৮), "Linear Hypotheses," International Encyclopedia of Statistics. Free Press, v. ১, Evan J. Williams, "I. Regression," পৃষ্ঠা ৫২৩-৫৪১। Julian C. Stanley, "II. Analysis of Variance," পৃষ্ঠা ৫৪১-৫৫৪।
- Lindley, D.V. (১৯৮৭), "Regression and correlation analysis," New Palgrave: A Dictionary of Economics, v. ৪, পৃষ্ঠা ১২০-১২৩।
- Birkes, David and Dodge, Y., Alternative Methods of Regression. আইএসবিএন ০-৪৭১-৫৬৮৮১-৩।
- Chatfield, C. (১৯৯৩), "Calculating Interval Forecasts," Journal of Business and Economic Statistics, ১১। পৃষ্ঠা ১২১-১৩৫।
- Draper, N.R.; Smith, H. (১৯৯৮)। Applied Regression Analysis (৩য় সংস্করণ)। John Wiley। আইএসবিএন 978-0-471-17082-2।
- Fox, J. (১৯৯৭), Applied Regression Analysis, Linear Models and Related Methods. Sage।
- Hardle, W., Applied Nonparametric Regression (১৯৯০), আইএসবিএন ০-৫২১-৪২৯৫০-১।
- Meade, Nigel; Islam, Towhidul (১৯৯৫)। "Prediction intervals for growth curve forecasts"। ১৪ (৫): ৪১৩–৪৩০। ডিওআই:10.1002/for.3980140502।
- A. Sen, M. Srivastava, Regression Analysis — Theory, Methods, and Applications, Springer-Verlag, Berlin, ২০১১ (৪র্থ মুদ্রণ)।
- T. Strutz: Data Fitting and Uncertainty (A practical introduction to weighted least squares and beyond). Vieweg+Teubner, আইএসবিএন ৯৭৮-৩-৮৩৪৮-১০২২-৯।
- Malakooti, B. (২০১৩)। Operations and Production Systems with Multiple Objectives। John Wiley & Sons।
বহিঃসংযোগ[সম্পাদনা]
- Hazewinkel, Michiel, সম্পাদক (২০০১), "Regression analysis", Encyclopedia of Mathematics, Springer Science+Business Media, আইএসবিএন 978-1-55608-010-4
- Earliest Uses: Regression – মৌলিক ইতিহাস এবং তথ্য সূত্রাবলি
- Regression of Weakly Correlated Data – X-সীমার তুলনায় Y-সীমা যথেষ্ট ক্ষুদ্রতর হলে কীভাবে রৈখিক নির্ভরণে ত্রুটির উদ্রেক ঘটে।












































































