গেয়র্গ কান্টর
এই নিবন্ধের ইংরেজি পরিভাষা ও উইকিসংযোগগুলির অনুবাদ প্রয়োজন।টির রচনা সংশোধনের প্রয়োজন হতে পারে। কারণ ব্যাকরণ, রচনাশৈলী, বানান বা বর্ণনাভঙ্গিগত সমস্যা রয়েছে। |
গেয়র্গ কান্টর | |
|---|---|
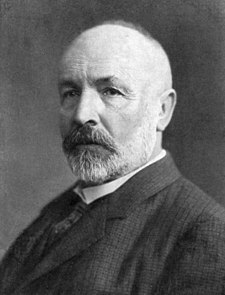 | |
| জন্ম | গেয়র্গ ফের্ডিনান্ড লুডভিগ ফিলিপ কান্টর ৩ মার্চ ১৮৪৫ |
| মৃত্যু | ৬ জানুয়ারি ১৯১৮ (বয়স ৭২) |
| মাতৃশিক্ষায়তন | ইটিএইচ জুরিখ, ইউনিভার্সিটি অফ বার্লিন |
| পরিচিতির কারণ | সেট তত্ত্ব |
| বৈজ্ঞানিক কর্মজীবন | |
| কর্মক্ষেত্র | গণিত |
| প্রতিষ্ঠানসমূহ | ইউনিভার্সিটি অফ হালে |
| ডক্টরাল উপদেষ্টা | আর্নস্ট কামার কার্ল ভায়েরস্ট্রাস |
| ডক্টরেট শিক্ষার্থী | আলফ্রেড বামেক |
গেয়র্গ ফের্ডিনান্ড লুডভিগ ফিলিপ কান্টর[টীকা ১] (জার্মান: Georg Ferdinand Ludwig Philipp Cantor; উচ্চারণ: গেয়ক্ ফেয়াডিনান্ট্ লুড্ভিক্ ফিলিপ্ কান্টোয়া) (৩ মার্চ [পুরোনো শৈলীতে ১৯ ফেব্রুয়ারি] ১৮৪৫ [১] – ৬ জানুয়ারি, ১৯১৮) একজন জার্মান গণিতবিদ যিনি তার সেট তত্ত্ব সংক্রান্ত কাজের জন্য সুপরিচিত, যা গণিতের একটি ভিত্তিসূচক তত্ত্বে পরিণত হয়েছে। কান্টর সেটের মধ্যে ঐকিক সম্বন্ধ (one-to-one correspondence) স্থাপনের গুরুত্ব প্রতিষ্ঠা করেন, অসীম এবং সুবিন্যস্ত সেটকে সংজ্ঞায়িত করেন, এবং প্রমাণ করেন যে বাস্তব সংখ্যা স্বাভাবিক সংখ্যার চাইতে সংখ্যায় বেশি। প্রকৃতপক্ষে কান্টরের তত্ত্ব "অসীম সংখ্যক অসীমের" ধারণা দেয়। তিনি অংকবাচক এবং ক্রমবাচক সংখ্যা এবং তাদের পাটীগণিতের সংজ্ঞা দেন। কান্টরের গবেষণাকর্মের অত্যন্ত গুরুত্বপূর্ণ দার্শনিক গুরুত্ব ছিল, যা সম্বন্ধে তিনি ভালোভাবেই অবহিত ছিলেন।[২]
কান্টরের সীমাতিক্রমী সংখ্যার (transfinite number) ধারণাটি প্রকৃতপক্ষে এতটাই স্বাভাবিক কাণ্ডজ্ঞান পরিপন্থী — এমনকি অবিশ্বাস্য — হিসেবে বিবেচিত হয়েছিল যে সেটি সমসাময়িক গণিতবিদ লেওপোল্ড ক্রোনেকার (Leopold Kronecker) এবং অঁরি পোয়াঁকারের কাছ থেকে প্রতিরোধের সম্মুখীন হয়[৩] এবং পরবর্তীতে হের্মান ভাইল এবং এল.ই.জে. ব্রাউয়েরও তার বিপক্ষে অবস্থান গ্রহণ করেন; এমনকি লুডভিগ ভিটগেনষ্টাইন তার তত্ত্বের বিরুদ্ধে দার্শনিক অসঙ্গতির অভিযোগ উত্থাপন করেন। কিছু খ্রিস্টান ধর্মতাত্ত্বিক কান্টরের ঈশ্বরের প্রকৃতির পরম অসীমতার বিরুদ্ধে চ্যালেঞ্জ হিসেবে দেখেন,[৪] এবং এক পর্যাটে তারা সীমাতিক্রমী সংখ্যার তত্ত্বকে সর্বেশ্বরবাদের সমতুল্য ঘোষণা করেন।[৫] কিছু ক্ষেত্রে তার কাজের চরম বিরুদ্ধাচার করা হয়: পয়েনকেয়ার কান্টরের ধারণাকে গণিতের শৃঙ্খলায় একটি "গভীর অসুখ" হিসেবে বর্ণনা করেন[৬] এবং ক্রোনেকার সর্বসমক্ষে কান্টরের বিরুদ্ধাচরণ করেন এবং তাকে ব্যক্তিগত আক্রমণ করে "হাতুড়ে বৈজ্ঞানিক", "বিশ্বাসঘাতক" এবং "তারুণ্যের অবক্ষয়কারী" হিসেবে দাবী করেন।[৭] কান্টরের মৃত্যুর কয়েক দশক পর এক লেখায় ভিটগেনস্টেইন অনুতাপ করেন যে, গণিত "সেট তত্ত্বের ক্ষতিকারক বাগবিতণ্ডায় গভীরভাবে আক্রান্ত হয়ে পড়েছে" এবং একে "গাঁজাখুরি", "হাস্যকর" ও "ভুল" বলে উড়িয়ে দেন।[৮] বয়স মধ্য-ত্রিশের পর থেকেই কান্টর মাঝে মধ্যেই বিষন্নতায় আক্রান্ত হতেন এবং এর জন্যে তার গাণিতিক ধারণাগুলি নিয়ে সমসাময়িক গণিতবিদদের বিতর্ককে দায়ী করা হত,[৯] তবে বর্তমানে তার অসুখটিকে সম্ভাব্য বাইপোলার ডিসঅর্ডারের উপসর্গ হিসেবে মনে করা হয়।[১০]
এই বিষম সমালোচনার উপশম তিনি পরবর্তীতে উষ্ণ সংবর্ধনায় লাভ করেন। ১৯০৪ সালে কান্টরকে সিলভেস্টার পদকে ভূষিত করা হয়, যা সেসময় গণিতের সর্বোচ্চ সম্মান হিসেবে বিবেচিত ছিল।[১১] কান্টর বিশ্বাস করতেন তার সীমাতিক্রমী সংখ্যার তত্ত্ব স্বয়ং ঈশ্বর তার ওপর অবতীর্ণ করেছেন।[১২] গণিতবিদ ডাভিড হিলবের্ট কান্টরের সমালোচনার বিরুদ্ধে এই বিখ্যাত উক্তিটি করেন: "কান্টর আমাদের জন্য যে স্বর্গ রচনা করে গেছেন, তা থেকে কেউ আমাদেরকে বহিস্কার করতে পারবে না"।[১৩]
জীবনবৃত্তান্ত[সম্পাদনা]
যৌবন ও শিক্ষাজীবন[সম্পাদনা]
কান্টর ১৮৪৫ সালে রাশিয়ার সাংত পিতেরবুর্গ শহরে জন্মগ্রহণ করেছিলেন এবং তার জীবনের প্রথম এগারো বছর সেখানেই কাটান। কান্টর ছিলেন ছয় ভাইবোনের মধ্যে জ্যেষ্ঠতম। তার বেহালাবাদনে ভালো পারদর্শিতা ছিল, যা ছিল তার পিতামাতার সাঙ্গীতিক ও শৈল্পিক প্রতিভার ধারাবাহিকতা। তার পিতা ছিলেন সেন্ট পিটার্সবার্গ শেয়ারবাজারের সদস্য; তিনি অসুস্থ হয়ে পড়লে তার পরিবার নিয়ে ১৮৫৬ সালে জার্মানিতে স্থানান্তরিত হন। কান্টর ড্রামষ্টাট শহরের রেয়ালশুলে থেকে সম্মানসহ স্নাতক হন; তার গণিতে বিস্ময়কর দক্ষতা, বিশেষতঃ ত্রিকোণমিতিতে তার পারদর্শিতা ছিল সুবিদিত। ১৮৬২ সালে কান্টর সুইজারল্যান্ডের জুরিখ নগরীর ফেডারেল পলিটেকনিক ইনস্টিটিউটে ভর্তি হন, যা আজ ইটিএইচ জুরিখ নামে পরিচিত। ১৮৬৩ সালে তার পিতার মৃত্যুর পর উল্লেখযোগ্য পরিমাণ সম্পত্তির উত্তরাশিকার লাভ করে কান্টর বার্লিন বিশ্ববিদ্যালয়ে স্থানান্তরিত হন এবং সেখানে লেওপোল্ড ক্রোনেকার, কার্ল ভাইয়ারষ্ট্রাস এবং এর্নস্ট কুমারের বক্তৃতা শ্রবণ করতেন। তিনি ১৮৬৬ সালের গ্রীষ্মকাল গ্যোটিগেন বিশ্ববিদ্যালয়ে কাটান, যা ছিল তখনকার ও পরবর্তী সময়ে গাণিতিক গবেষণার একটি গুরুত্বপূর্ণ প্রতিষ্ঠান। ১৮৬৭ সালে তিনি সংখ্যা তত্ত্বের ওপর গবেষণা কর্মের জন্যে বার্লিন বিশ্ববিদ্যালয় হতে পিএইচডি উপাধি লাভ করেন।
টীকা[সম্পাদনা]
- ↑ এই জার্মান ব্যক্তি বা স্থাননামটির বাংলা প্রতিবর্ণীকরণে উইকিপিডিয়া:বাংলা ভাষায় জার্মান শব্দের প্রতিবর্ণীকরণ শীর্ষক রচনাশৈলী নিদের্শিকাতে ব্যাখ্যাকৃত নীতিমালা অনুসরণ করা হয়েছে।
তথ্যসূত্র[সম্পাদনা]
- ↑ Grattan-Guinness 2000, p. 351
- ↑ The biographical material in this article is mostly drawn from Dauben 1979. Grattan-Guinness 1971, and Purkert and Ilgauds 1985 are useful additional sources.
- ↑ Dauben 2004, p. 1.
- ↑ Dauben, 1977, p. 86; Dauben, 1979, pp. 120 & 143.
- ↑ উদ্ধৃতি ত্রুটি:
<ref>ট্যাগ বৈধ নয়;daub77102নামের সূত্রটির জন্য কোন লেখা প্রদান করা হয়নি - ↑ Dauben 1979, p. 266.
- ↑ Dauben 2004, p. 1. See also Dauben 1977, p. 89 15n.
- ↑ উদ্ধৃতি ত্রুটি:
<ref>ট্যাগ বৈধ নয়;Rodychনামের সূত্রটির জন্য কোন লেখা প্রদান করা হয়নি - ↑ Dauben 1979, p. 280:"...the tradition made popular by Arthur Moritz Schönflies blamed Kronecker's persistent criticism and Cantor's inability to confirm his continuum hypothesis" for Cantor's recurring bouts of depression.
- ↑ Dauben 2004, p. 1. Text includes a 1964 quote from psychiatrist Karl Pollitt, one of Cantor's examining physicians at Halle Nervenklinik, referring to Cantor's mental illness as "cyclic manic-depression".
- ↑ উদ্ধৃতি ত্রুটি:
<ref>ট্যাগ বৈধ নয়;daub248নামের সূত্রটির জন্য কোন লেখা প্রদান করা হয়নি - ↑ Dauben 2004, pp. 8, 11 & 12-13.
- ↑ Hilbert 1926, p. 170; see Reid 1996, p. 177
বহিঃসংযোগ[সম্পাদনা]
- ও'কনর, জন জে.; রবার্টসন, এডমুন্ড এফ., "গেয়র্গ কান্টর", ম্যাকটিউটর গণিতের ইতিহাস আর্কাইভ, সেন্ট অ্যান্ড্রুজ বিশ্ববিদ্যালয়।
- ও'কনর, জন জে.; রবার্টসন, এডমুন্ড এফ., "A history of set theory", ম্যাকটিউটর গণিতের ইতিহাস আর্কাইভ, সেন্ট অ্যান্ড্রুজ বিশ্ববিদ্যালয়। Mainly devoted to Cantor's accomplishment.
- গণিত উদ্ভববিজ্ঞান প্রকল্পে গেয়র্গ কান্টর
- Selections from Cantor's philosophical writing.
- Text of Cantor's 1891 diagonal argument.
- Stanford Encyclopedia of Philosophy: Set theory by Thomas Jech.
- Grammar school Georg-Cantor Halle (Saale): Georg-Cantor-Gynmasium Halle
| এই নিবন্ধটি অসম্পূর্ণ। আপনি চাইলে এটিকে সম্প্রসারিত করে উইকিপিডিয়াকে সাহায্য করতে পারেন। |
