হুইটস্টোন সেতু
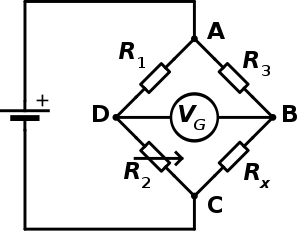
হুইটস্টোন সেতু মূলত অজানা রোধের মান নির্ণয় করতে ব্যবহৃত হয়। সেতু বর্তনীটিতে তড়িৎ প্রবাহে ভারসাম্য এনে বর্তনীর অজানা রোধের পরিমাপ করা হয়। সেতুর একটি বাহুতে অজানা রোধটি থাকে। বর্তনীর প্রাথমিক সুবিধা হলো এটি দ্বারা অত্যন্ত নির্ভুলভাবে পরিমাপ করা যায় (সাধারণ বিভব বিভাজক বিধি দিয়ে এ সূক্ষ্ম পরিমাপ নেওয়া যায় না)।[১][২] এর কার্যপ্রণালি মূলত বিভব মাপকের মতো।
১৮৩৩ সালে স্যামুয়েল হান্টার ক্রিস্টি এ সেতু উদ্ভাবন করেছিলেন এবং ১৮৪৩ সালে স্যার চার্লস হুইটস্টোন এটিকে উন্নত এবং জনপ্রিয় করে তুলেছিলেন। হুইটস্টোন সেতুর অন্যতম প্রাথমিক ব্যবহার ছিল মাটি পরীক্ষণ এবং তুলনা করা।[৩]
কার্যপ্রণালী[সম্পাদনা]
চিত্র অনুযায়ী, হল স্থির কিন্তু অজানা রোধ, যার মান পরিমাপ করতে হবে।
এবং জানা রোধ মাপের রোধক। এর মধ্যে এর রোধের মান নিয়ন্ত্রণযোগ্য। এর মানকে ততক্ষণ পরিবর্তন করা হয় যতক্ষণ না সেতু "ভারসাম্য" অর্জন করে এবং গ্যালভানোমিটার এর মধ্য দিয়ে কোনও তড়িৎ প্রবাহিত হয় না। এই সময়ে, দুটি মধ্য বিন্দুর (B এবং D) মধ্যে বিভব হবে শূন্য। সুতরাং দুটি বাহুতে দুটি জানা রোধের অনুপাত অজানা বাহুর দুটি রোধের অনুপাতের সমান। সেতু যদি ভারসাম্যহীন থাকে, তড়িতের অভিমুখ থেকে বোঝা যায় কমানো বা বাড়ানো লাগবে কিনা।
ভারসাম্যের সময়,
একটি গ্যালভানোমিটার দিয়ে তড়িৎ প্রবাহ হচ্ছে কি না তা অত্যন্ত নির্ভুলভাবে পর্যবেক্ষণ করা যেতে পারে। অতএব, যদি এবং নির্ভুল ভাবে জানা থাকে, তাহলে কেও নির্ভুল ভাবে পরিমাপ করা যেতে পারে। এর খুব ছোট পরিবর্তন হলেও ভারসাম্য ব্যাহত হয় এবং সহজেই বোঝা যেতে পারে।
অন্যভাবে, যদি এবং জ্ঞাত হয়, কিন্তু নিয়ন্ত্রনযোগ্য না হয়, মিটার জুড়ে বিভব পার্থক্য বা মিটারের মধ্যে দিয়ে তড়িৎ প্রবাহের মান ব্যবহার করে এর মান নির্ণয় করা যায়। এর জন্য কার্শফের বর্তনীর সমীকরণসমূহ দরকার হয়। এই বিন্যাসটি প্রায়শই বিকৃতি মাপন এবং রোধ থার্মোমিটার দিয়ে পরিমাপের ক্ষেত্রে ব্যবহৃত হয়। এর বড় কারণ হল একটি রোধকে শূন্য বিভবে নিয়ে আসার থেকে, কোন মিটার থেকে বিভবের পরিমাপ করা অনেক দ্রুত ও সহজ হয়।
সমীকরণ গঠন[সম্পাদনা]

ভারসাম্যের সময় উদ্ভূত সমীকরণ[সম্পাদনা]
ভারসাম্যের সময়, দুটি মধ্যবিন্দুর (B এবং D) মধ্যে বিভব এবং তড়িৎ প্রবাহ দুটিই শূন্য। অতএব, , , , এবং:
কার্শফের বর্তনীর সমীকরণসমূহ ব্যবহার করে সম্পূর্ণ সমীকরণ গঠন[সম্পাদনা]
প্রথমে, কার্শফের প্রথম সূত্র ব্যবহার করে B and D এর সংযোগস্থল দুটিতে তড়িৎপ্রবাহের মান বের করা হয়:
তারপর, কার্শফের দ্বিতীয় সূত্র ব্যবহার করে বর্তনী ABDA এবং BCDBতে বিভবের মান বের করা হয়:
যখন সেতু ভারসাম্যে থাকে, তখন IG = 0, সুতরাং দ্বিতীয় দফার সমীকরণগুলি আবারও লেখা যেতে পারে এই ভাবে:
তারপর সমীকরণ (2) কে সমীকরণ (1) দিয়ে ভাগ করা হয় এবং ফলাফল সমীকরণ পুনরায় সাজানো হয়, এতে পাওয়া যায়:
যেহেতু: I3 = Ix এবং I1 = I2 সমানুপাতিক, ওপরে কার্শফের প্রথম সূত্র থেকে পাওয়া গেছে, অতএব I3 I2 / I1 Ix উপরের সমীকরণটি থেকে বাতিল হয়ে যায়। সুতরাংRx এর কাঙ্ক্ষিত মান এখন পাওয়া যাচ্ছে, যেটি হল:
অন্যদিকে, যদি গ্যালভানোমিটারের রোধের মান যথেষ্ট বেশি থাকে, যাতে IG এর মান নগণ্য হয়, তবে অন্য তিনটি রোধের মান থেকে এবং সরবরাহিত বিভব (VS) থেকে Rx এর মান, অথবা চারটি রোধের মান থেকে সরবরাহিত বিভব নির্ণয় করা সম্ভব। এটি করার জন্য, প্রত্যেক বিভব বিভাজক থেকে বিভব বের করতে হবে এবং একের থেকে অন্যটিকে বিয়োগ করতে হবে। এর জন্য সমীকরণগুলি হল:
যেখানে VG হল সংযোগস্থল B এর সাপেক্ষে সংযোগস্থল D এর বিভব
তাৎপর্য[সম্পাদনা]
হুইটস্টোন সেতু একটি পার্থক্য পরিমাপের ধারণা ব্যাখ্যা করে এবং এই পরিমাপ অত্যন্ত সঠিক হতে পারে। হুইটস্টোন সেতু ব্যবহার করে ধারকত্ব, প্রেরকত্ব, সামগ্রিক প্রতিরোধ পরিমাপ করা যেতে পারে। এছাড়াও অন্যান্য রাশি, যেমন: একটি বিস্ফোরক মাপক যন্ত্র দিয়ে একটি নমুনায় দহনযোগ্য গ্যাসের পরিমাণ নির্ণয় করা যেতে পারে। খুব কম মানের রোধের পরিমাপের জন্য হুইটস্টোন সেতু থেকে বিশেষভাবে রূপান্তরিত করে কেলভিন সেতু তৈরি হয়েছিল। অনেক ক্ষেত্রে, অজানা রোধের পরিমাপের তাৎপর্য কিছু ভৌত ঘটমান বিষয়ের (যেমন বল, তাপমাত্রা, চাপ ইত্যাদি) প্রভাব পরিমাপের সাথে সম্পর্কিত যার ফলে এই রাশিগুলি পরোক্ষভাবে পরিমাপ করার ক্ষেত্রে হুইটস্টোন সেতু ব্যবহার করা যায়।
১৮৬৫ সালে জেমস ক্লার্ক ম্যাক্সওয়েল এই ধারণাটি দিয়ে পরিবর্তী তড়িৎ প্রবাহেও কাজে লাগিয়েছিলেন এবং ১৯২৬ সালের দিকে অ্যালান ব্লুমলিন তার ব্লুমলিন ব্রিজ তৈরি করে বিষয়টিকে আরও উন্নত করেছিলেন।[৪]
মৌলিক সেতুর পরিবর্তনসমূহ[সম্পাদনা]

হুইটস্টোন সেতু হল মৌলিক সেতু, তবে মৌলিক হুইটস্টোন সেতুটি উপযুক্ত না হলে বিভিন্ন ধরনের রোধের পরিমাপ করার জন্য অন্যান্য অনেক পরিবর্তন করা হয়েছে। কিছু পরিবর্তনগুলি হল:
- কেরি ফস্টার সেতু, ছোট রোধ পরিমাপের জন্য
- কেলভিন সেতু, ছোট চার-প্রান্তীয় রোধগুলি পরিমাপ করার জন্য
- ম্যাক্সওয়েল সেতু, এবং ওয়েন সেতু প্রতিঘাত উপাদানগুলি পরিমাপ করার জন্য।
তথ্যসূত্র[সম্পাদনা]
- ↑ "Circuits in Practice: The Wheatstone Bridge, What It Does, and Why It Matters", as discussed in this MIT ES.333 class video ওয়েব্যাক মেশিনে আর্কাইভকৃত ৭ সেপ্টেম্বর ২০১৯ তারিখে
- ↑ Robbins, Allan H.; Miller, Wilhelm C. (২০১৩)। Circuit Analysis: Theory and Practice। ভারত: Cengage Learning। আইএসবিএন 978-81-315-1902-8।
- ↑ "The Genesis of the Wheatstone Bridge" by Stig Ekelof discusses Christie's and Wheatstone's contributions, and why the bridge carries Wheatstone's name. Published in "Engineering Science and Education Journal", volume 10, no 1, February 2001, pages 37–40.
- ↑ "The Life and Times of A D Blumlein" (পিডিএফ)। ১২ অক্টোবর ২০২০ তারিখে মূল (পিডিএফ) থেকে আর্কাইভ করা। সংগ্রহের তারিখ ১১ অক্টোবর ২০২০।
বহিঃসংযোগ[সম্পাদনা]
- DC Metering Circuits chapter from Lessons In Electric Circuits Vol 1 DC free ebook and Lessons In Electric Circuits series.
- Test Set I-49









![{\displaystyle {\begin{aligned}{\frac {R_{2}}{R_{1}}}&={\frac {R_{x}}{R_{3}}}\\[4pt]\Rightarrow R_{x}&={\frac {R_{2}}{R_{1}}}\cdot R_{3}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d10637c0ae2c1ef7ee40aa0d5f8cce2108367b7)




![{\displaystyle {\begin{aligned}{\frac {V_{DC}}{V_{AD}}}&={\frac {V_{BC}}{V_{AB}}}\\[4pt]\Rightarrow {\frac {I_{2}R_{2}}{I_{1}R_{1}}}&={\frac {I_{x}R_{x}}{I_{3}R_{3}}}\\[4pt]\Rightarrow R_{x}&={\frac {R_{2}}{R_{1}}}\cdot R_{3}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cfdba1cb0ab60efec1f88e7472356444001b5cb2)





![{\displaystyle {\begin{aligned}V_{G}&=\left({R_{2} \over {R_{1}+R_{2}}}-{R_{x} \over {R_{x}+R_{3}}}\right)V_{s}\\[6pt]R_{x}&={{R_{2}\cdot V_{s}-(R_{1}+R_{2})\cdot V_{G}} \over {R_{1}\cdot V_{s}+(R_{1}+R_{2})\cdot V_{G}}}R_{3}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5afea72ff716d2e8479994fe33f8815fcdc0a4dd)