ডোমেইন কালারিং

ডোমেইন কালারিং হচ্ছে কমপ্লেক্স ভেরিয়েবলের ফাংশন গুলো কে চিত্রিত করণের একটা পদ্ধতি। “ডোমেইন কালারিং” শব্দটা ১৯৯৮ সালের দিকে প্রথম ব্যবহার করেন ফ্রাঙ্ক ফেরিস [১]। কিন্তু ধারাবাহিক রঙ ব্যবহার করে ডোমেইন থেকে কো-ডোমেইনে বা ইমেজ প্লেনে ম্যাপ করার পদ্ধতিটা ১৯৯৯ সালে সর্বপ্রথম ব্যবহার করেন জর্জ আডো এবং পল গডফ্রে [২] গ্রাফিক্সে কালার গ্রিডের মাধ্যমে একে প্রকাশ করেন ডাহ্‌ আর্নল্ড ১৯৯৭ সালে [৩]।

সূচিপত্র

১ মোটিভেশন
- ১.১ অপ্রতুল মাত্রা
- ১.২ জটিল সংখ্যার ভিজ্যুয়াল এনকোডিং
২ উদাহরণ
৩ তথ্যসূত্র
৪ বহিঃসংযোগ সমূহ

[সম্পাদনা] মোটিভেশন

[সম্পাদনা] অপ্রতুল মাত্রা

একটি বাস্তব সংখ্যার ফাংশন $f:\mathbb{R}\rightarrow{}\mathbb{R}$ (যেমন $f(x)=x^{2}$ ) কে লেখ চিত্রে দুইটি কার্তেসীয় কো-অর্ডিনেট ব্যবহার করে একটা সমতলে অঙ্কন করা সম্ভব। একটি জটিল সংখ্যার ফাংশন $g:\mathbb{C}\rightarrow{}\mathbb{C}$ যেটার স্বাধীন চলক একটি এমনকি, তারও দুইটি জটিল বা কাল্পনিক ডাইমেনশ থাকে। যেহুতু জটিল সমতল নিজেই দিমাত্রিক সেহেতু একটা জটিল সংখ্যার ফাংশন তার দিমাত্রিক আর্গুমেন্ট এবং দিমাত্রিক ভ্যালু নিয়ে আসলে একটা চতুর্মাত্রিক সিস্টেম। একারণে ত্রিমাত্রিক জগতে সেটাকে চিত্রিত করা মুশকিল। অবশ্য হোমোমর্ফিক ফাংশন সমূহ রিম্যান সার্ফেসের সাহায্যে প্রকাশ করা সম্ভব।

[সম্পাদনা] জটিল সংখ্যার ভিজ্যুয়াল এনকোডিং

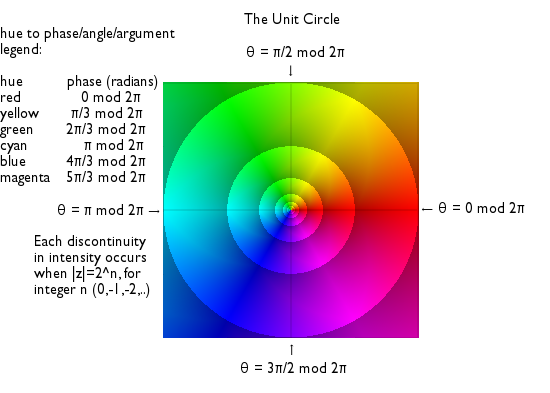
কোন একটা জটিল সংখ্যা $z=re^{i\theta}$ , এর ফেজ বা দশা(আরেক নাম আর্গুমেন্ট) $\theta \,$ কে হিউ বা রঙের পার্থক্য দ্বারা এবং মডুলাস বা মান $r=|z|$ কে তীব্রতা বা তীব্রতার পার্থক্য দ্বারা প্রকাশ করা হয়। দশা বোঝানোর জন্য রঙ গুলোকে ইচ্ছা মত নির্ধারণ করা যেতে পারে। তবে মাঝে মাঝে সেটা কালার হুইল অনুসারে হয়। কখনো কখনো দশা কে রঙের বদলে নির্দিষ্ট গ্রাডিয়েন্ট দ্বারা প্রকাশ করা হয়।

[সম্পাদনা] উদাহরণ

নিম্নে জটিল সংখ্যার সাইন ফাংশন $w=\sin(z)$ কে বাস্তব অক্ষ বরাবর $-2\pi$ থেকে $2\pi$ এবং কাল্পনিক অক্ষ বরাবর $-1.5$ থেকে $1.5$ পর্যন্ত নিয়ে উপরিউক্ত পদ্ধতিতে আঁকা হল।