প্রতিফলন (পদার্থবিজ্ঞান)

যে সকল বস্তু নিজে থেকেই আলো বিকিরণ করে তাদেরকে আলোক উৎস (source of light) বলা হয়। এই আলোক উৎস দুই ধরনের হতে পারে- ১) স্বপ্রভ বা স্বয়ংপ্রভ বা দীপ্তিমান উৎস (luminous or self-luminous source) ও ২) নিষ্প্রভ বা অপ্রভ বা দীপ্তিহীন উৎস (non-luminous source)।
স্বপ্রভ বা স্বয়ংপ্রভ বা দীপ্তিমান উৎস বা বস্তু: সেইসব আলোক উৎস বা বস্তু যেগুলি নিজের আলো নিজেই বিকিরণ করে (অর্থাৎ নিজের আলো নিজেই উৎপন্ন করে) সেইসকল উৎস বা বস্তু কে স্বপ্রভ বা স্বয়ংপ্রভ বা দীপ্তিমান উৎস বা বস্তু বলে । যেমন: সূর্য, নক্ষত্র, বৈদ্যুতিক বাল্ব, জ্বলন্ত মোমবাতি ইত্যাদি।
নিষ্প্রভ বা অপ্রভ দীপ্তিহীন উৎস বা বস্তু: যেইসকল বস্তুর নিজস্ব কোনো আলো নেই, স্বপ্রভ বা দীপ্তিমান বস্তু থেকে পাওয়া আলো প্রতিফলিত করে আলোকিত হয়, সেইসব বস্তুকে নিষ্প্রভ বা অপ্রভ বা দীপ্তিহীন উৎস বা বস্তু বলে।
আমাদের চারপাশের বস্তুগুলির অধিকাংশই হল নিষ্প্রভ বা বস্তু। চাঁদ ও গ্রহগুলিও হল নিষ্প্রভ বা দীপ্তিহীন। এই বস্তুগুলি সূর্যের আলো প্রতিফলিত করে বলেই আমরা এদেরকে আলোকিত দেখি। সুতরাং আলোর প্রতিফলন না ঘটলে আমরা কোনো নিষ্প্রভ বা দীপ্তিহীন বস্তুকে দেখতেই পেতাম না। যেমন দিনের বেলায় আকাশে সূর্য দেখতে পেতাম ঠিকই, কিন্তু রাস্তাঘাট, ঘরবাড়ি ইত্যাদি সবকিছুই দৃষ্টির অগোচরে থাকত। স্পষ্টতই আলোর প্রতিফলন আমাদের দৈনন্দিন জীবনে অত্যন্ত গুরুত্বপূর্ণ একটি ঘটনা।
আলোর প্রতিফলন[সম্পাদনা]
আলো এক প্রকার শক্তি। আলো কোনো স্বচ্ছ মাধ্যমের ভিতর দিয়ে যাওয়ার সময় অন্য কোন মাধ্যমে বাধা পেলে দুই মাধ্যমের বিভেদতল থেকে কিছু পরিমাণ আলোক রশ্মি আগের মাধ্যমে ফিরে আসে, এ ঘটনাকে আলোর প্রতিফলন বলে।[১] অথবা আলোক উৎস থেকে আপতিত রশ্মি কোন তলে বা পৃষ্ঠে বাধা পেলে কিছু আলো পুনরায় আগের মাধ্যমে ফিরে আসে, এ ঘটনাকে আলোর প্রতিফলন বলে।

আলোর প্রতিফলনের একটি অন্যতম উদাহরণ হল- সমতল দর্পণ বা আয়নার সামনে আমরা যখন দাঁড়াই তখন আমরা আমাদের প্রতিবিম্ব দেখতে পাই। দর্পণে আলোর প্রতিফলনের জন্যেই বিম্বের সৃষ্টি হয়।
আলোর প্রতিফলন সাধারণত দুটি বিষয়ের উপর নির্ভর করে: আলোর আপতন কোণ ও মাধ্যমগুলোর প্রকৃতি। আপতিত রশ্মি যত বেশি কোণে আপতিত হবে এবং প্রতিফলক যত বেশি মসৃণ হবে আলোর প্রতিফলন তত বেশি হবে। পক্ষান্তরে, অমসৃণ কিংবা স্বচ্ছ প্রতিফলক থেকে আলোর প্রতিফলন কম হয়।
প্রতিফলনের শ্রেণিবিভাগ[সম্পাদনা]
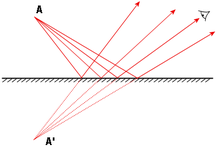

প্রতিফলক পৃষ্ঠের প্রকৃতি আনুযায়ী আলোর প্রতিফলন দু ধরনের হতে পারে, যথাঃ নিয়মিত প্রতিফলন ও ব্যাপ্ত প্রতিফলন।
নিয়মিত বা সুষম প্রতিফলন[সম্পাদনা]
যখন একগুচ্ছ সমান্তরাল আলোকরশ্মি কোন মসৃণ পৃষ্ঠে আপতিত হয়ে প্রতিফলনের পর সমান্তরাল থাকে বা অভিসারী কিংবা অপসারীগুচ্ছে পরিণত হয়, তবে আলোর সেই প্রতিফলনকে নিয়মিত বা সুষম প্রতিফলন বলে। প্রতিফলক পৃষ্ঠ মসৃণ হলে যেমন- সমতল দর্পণে আলোর নিয়মিত প্রতিফলন হয়। এক্ষেত্রে প্রতিটি আলোক রশ্মির আপতন কোণ সমান হয় ও প্রতিফলন কোণগুলোও সমান হয়। গ্রিসের প্রখ্যাত গণিতবিদ এবং ইঞ্জিনিয়ার- হীরন[২][৩] সর্বপ্রথম আলোর নিয়মিত প্রতিফলনের ধর্ম লক্ষ্য করেন।
অনিয়মিত বা ব্যাপ্ত প্রতিফলন[সম্পাদনা]
যদি একগুচ্ছ সমান্তরাল আলোক রশ্মি কোন পৃষ্ঠে আপতিত হয়ে প্রতিফলনের পর অসমান্তরাল হয় বা অভিসারী বা অপসারীগুচ্ছে পরিণত না হয় তবে আলোর সেই প্রতিফলনকে ব্যাপ্ত বা বিক্ষিপ্ত বা অনিয়মিত প্রতিফলন বলে। প্রতিফলক পৃষ্ঠ সমান্তরাল না হলে এরূপ হয়। এক্ষেত্রে সমান্তরাল রশ্মিগুলো প্রতিফলকপৃষ্ঠের বিভিন্ন বিন্দুতে বিভিন্ন কোণে আপতিত হয় বলে তাদের প্রতিফলন কোণও আলাদা হয়।প্রতিফলন এর উদাহরণ হিসেবে আয়না বলা যায়। এক্ষেত্রে আপতন কোন প্রতিফলন কোনের সমান হয়।
গুরুত্বপূর্ণ কিছু সংজ্ঞা[সম্পাদনা]
নিম্নে আপতিত রশ্মি, আপতন বিন্দু, অভিলম্ব, প্রতিফলিত রশ্মি, আপতন কোণ, প্রতিফলন কোণ এর সংজ্ঞা দেওয়া হল:
আপতিত রশ্মি[সম্পাদনা]
যে রশ্মি প্রতিফলকের উপর এসে পড়ে তাকে আপতিত রশ্মি বলে।
আপতন বিন্দু[সম্পাদনা]
আপতিত রশ্মি প্রতিফলকের উপর যে বিন্দুতে এসে পড়ে তাকে আপতন বিন্দু বলে।
অভিলম্ব[সম্পাদনা]
আপতন বিন্দুতে প্রতিফলকের উপর অঙ্কিত লম্বকে অভিলম্ব বলে।
প্রতিফলিত রশ্মি[সম্পাদনা]
প্রতিফলকে বাধা পেয়ে যে রশ্মি আগের মাধ্যমে ফিরে আসে তাকে প্রতিফলিত রশ্মি বলে।
আপতন কোণ[সম্পাদনা]
প্রতিফলকের ওপর আপতিত রশ্মি ও অভিলম্বের মধ্যবর্তী কোণকে আপতন কোণ বলে। একে “i” দ্বারা প্রকাশ করা হয়।

প্রতিফলন কোণ[সম্পাদনা]
প্রতিফলিত রশ্মি অভিলম্বের সাথে যে কোণ উৎপন্ন করে তাকে প্রতিফলন কোণ বলে। একে “r” দ্বারা প্রকাশ করা হয়।
আলোর প্রতিফলনের সূত্র[সম্পাদনা]
প্রতিফলক পৃষ্ঠ মসৃণ হলে আলোর প্রতিফলন প্রধানত দুটি সূত্র মেনে চলে, যথা-
- আপতিত রশ্মি, আপতন বিন্দুতে প্রতিফলকের উপর অভিলম্ব এবং প্রতিফলিত রশ্মি একই সমতলে থাকে।[১][৪]
- আপতন কোণ ও প্রতিফলন কোণ সর্বদা সমান হয়।[১][৪]
আরও দেখুন :[সম্পাদনা]
তথ্যসূত্র[সম্পাদনা]
- ↑ ক খ গ মাধ্যমিক পদার্থবিজ্ঞান বই (অধ্যায়-১৪; পৃষ্ঠা-১৮৪ থেকে ১৮৬)|রচনা:ড. শাহাজাহান তপন,মুহাম্মদ আজিজ হাসান,ড. রানা চৌধুরী|সম্পাদনা: ড. আলী আচসগল|প্রকাশক: জাতীয় শিক্ষাক্রম ও পাঠ্যপুস্তক বোর্ড,ঢাকা|সংস্করণ: ডিসেম্বর, ২০০৮
- ↑ Boyer (1968 [1991])। "Greek Trigonometry and Mensuration"। A History of Mathematics। পৃষ্ঠা 171–172।
At least from the days of Alexander the Great to the close of the classical world, there undoubtedly was much intercommunication between Greece and Mesopotamia, and it seems to be clear that the Babylonian arithmetic and algebraic geometry continued to exert considerable influence in the Hellenistic world. This aspect of mathematics, for example, appears so strongly in Heron of Alexandria (fl. ca. A.D. 100) that Heron once was thought to be Egyptian or Phoenician rather than Greek. Now it is thought that Heron portrays a type of mathematics that had long been present in Greece but does not find a representative among the great figures - except perhaps as betrayed by Ptolemy in the Tetrabiblos.
এখানে তারিখের মান পরীক্ষা করুন:|তারিখ=(সাহায্য) - ↑
Gregory A Tokaty (১৯৯৪)। A History and Philosophy of Fluid Mechanics। Courier Dover Publications। পৃষ্ঠা 26। আইএসবিএন 0-486-68103-3।
Grolier Incorporated (১৯৮৯)। Academic American Encyclopedia। Grolier University of Michigan। পৃষ্ঠা 144। আইএসবিএন 0-7172-2024-9।
Encyclopædia Britannica Online - Heron of Alexandria
Israel Shatzman, Michael Avi-Yonah (১৯৭৫)। Illustrated Encyclopedia of the Classical World। Harper and Row। পৃষ্ঠা 234। আইএসবিএন 0-06-010178-4।
Gillian Clements (২০০৫)। The Picture History of Great Inventors। frances lincoln ltd। পৃষ্ঠা 13। আইএসবিএন 0-7112-1605-3।
Enc. Britannica 2007, "Heron of Alexandria" - ↑ ক খ M. Nelkon (১৯৯৩)। "Light"। Principles of Physics (10th সংস্করণ)। Singapore: SHING LEE PUBLISHERS PTE LTD.। পৃষ্ঠা 260। আইএসবিএন 9971616688।
বহিঃসংযোগ[সম্পাদনা]
- Acoustic reflection ওয়েব্যাক মেশিনে আর্কাইভকৃত ৪ জানুয়ারি ২০১৯ তারিখে
