ফাজি লজিক
ফাজি লজিক এমন একটি যুক্তি ব্যবস্থা যেখানে কোন সমস্যার সমাধান ১ অথবা ০ ছাড়াও আরো বিভিন্ন উপায়ে দেওয়া যায়। বাইনারি ব্যাবস্থায় একটি সমস্যার সমাধান 'হ্যাঁ' অথবা 'না' - এই দু'টি উপায়ে দেয়া যায়। কিন্তু ফাজি লজিকে একটি সমস্যার সমাধান দুইয়ের অধিক উপায়ে দেওয়া যায়।[১] উদাহরণস্বরূপ, যদি প্রশ্ন করা হয় 'এখন কি রাত?' বাইনারী ব্যবস্থায় উত্তর হবে - 'হ্যাঁ' অথবা 'না'; অন্যদিকে, ফাজি লজিকে হ্যাঁ অথবা না ছাড়াও আরো উত্তর হতে পারে - মধ্যরাত, শেষরাত, সুবহে সাদিক ইত্যাদি।
ইতিহাস[সম্পাদনা]
১৯৬৫ সাথে সর্বপ্রথম ফাজি লজিক সম্পর্কে ধারণা দেন লতফি জাদেহ।[২][৩] তিনি একজন ইরানি ও আজারবাইজানী বংশোদ্ভূত মার্কিন কম্পিউটার বিজ্ঞানী। লতফি জাদেহকে ফাজি লজিকের জনক বলা হয়। তবে ফাজি লজিক ১৯২০-এর দশকে রচিত হয়েছে, অসীম মূল্যবান যুক্তি হিসেবে- বিশেষ করে উকাসিউইচ এবং টারস্কি রচিত।[৪]
ব্যবহার[সম্পাদনা]
ফাজি লজিকের ব্যবহার সর্বপ্রথম হয় জাপানে। বর্তমানে ফাজি লজিক পানির মান নিয়ন্ত্রণ, স্বয়ংক্রিয় রেল নিয়ন্ত্রণ, লিফট নিয়ন্ত্রণ, পারমাণবিক চুল্লি নিয়ন্ত্রণসহ গুরুত্বপূর্ণ নানা ক্ষেত্রে ব্যবহার হচ্ছে।
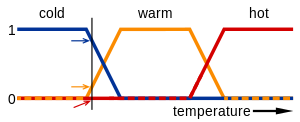
উদাহরণ[সম্পাদনা]
IF temperature IS very cold THEN stop fan
IF temperature IS cold THEN turn down fan
IF temperature IS normal THEN maintain fan
IF temperature IS hot THEN speed up fan
NOT x = (1 - truth(x))
x AND y = minimum(truth(x), truth(y))
x OR y = maximum(truth(x), truth(y))
x AND y = x*y
x OR y = 1-(1-x)*(1-y)
x OR y = NOT( AND( NOT(x), NOT(y) ) )
x OR y = NOT( AND(1-x, 1-y) )
x OR y = NOT( (1-x)*(1-y) )
x OR y = 1-(1-x)*(1-y)
x OR y = NOT( AND( NOT(x), NOT(y) ) )
x OR y = NOT( AND(1-x, 1-y) )
x OR y = NOT( (1-x)*(1-y) )
x OR y = 1-(1-x)*(1-y)
আরও দেখুন[সম্পাদনা]
গ্রন্থপঞ্জি[সম্পাদনা]
- Arabacioglu, B. C. (২০১০)। "Using fuzzy inference system for architectural space analysis"। Applied Soft Computing। 10 (3): 926–937। ডিওআই:10.1016/j.asoc.2009.10.011।
- Biacino, L.; Gerla, G. (২০০২)। "Fuzzy logic, continuity and effectiveness"। Archive for Mathematical Logic। 41 (7): 643–667। আইএসএসএন 0933-5846। ডিওআই:10.1007/s001530100128।
- Cox, Earl (১৯৯৪)। The fuzzy systems handbook: a practitioner's guide to building, using, maintaining fuzzy systems। Boston: AP Professional। আইএসবিএন 0-12-194270-8।
- Gerla, Giangiacomo (২০০৬)। "Effectiveness and Multivalued Logics"। Journal of Symbolic Logic। 71 (1): 137–162। আইএসএসএন 0022-4812। ডিওআই:10.2178/jsl/1140641166।
- Hájek, Petr (১৯৯৮)। Metamathematics of fuzzy logic। Dordrecht: Kluwer। আইএসবিএন 0-7923-5238-6।
- Hájek, Petr (১৯৯৫)। "Fuzzy logic and arithmetical hierarchy"। Fuzzy Sets and Systems। 3 (8): 359–363। আইএসএসএন 0165-0114। ডিওআই:10.1016/0165-0114(94)00299-M।
- Halpern, Joseph Y. (২০০৩)। Reasoning about uncertainty। Cambridge, Mass: MIT Press। আইএসবিএন 0-262-08320-5।
- Höppner, Frank; Klawonn, F.; Kruse, R.; Runkler, T. (১৯৯৯)। Fuzzy cluster analysis: methods for classification, data analysis and image recognition। New York: John Wiley। আইএসবিএন 0-471-98864-2।
- Ibrahim, Ahmad M. (১৯৯৭)। Introduction to Applied Fuzzy Electronics। Englewood Cliffs, N.J: Prentice Hall। আইএসবিএন 0-13-206400-6।
- Klir, George J.; Folger, Tina A. (১৯৮৮)। Fuzzy sets, uncertainty, and information। Englewood Cliffs, N.J: Prentice Hall। আইএসবিএন 0-13-345984-5।
- Klir, George J.; St Clair, Ute H.; Yuan, Bo (১৯৯৭)। Fuzzy set theory: foundations and applications। Englewood Cliffs, NJ: Prentice Hall। আইএসবিএন 0-13-341058-7।
- Klir, George J.; Yuan, Bo (১৯৯৫)। Fuzzy sets and fuzzy logic: theory and applications। Upper Saddle River, NJ: Prentice Hall PTR। আইএসবিএন 0-13-101171-5।
- Kosko, Bart (১৯৯৩)। Fuzzy thinking: the new science of fuzzy logic। New York: Hyperion। আইএসবিএন 0-7868-8021-X।
- Kosko, Bart; Isaka, Satoru (জুলাই ১৯৯৩)। "Fuzzy Logic"। Scientific American। 269 (1): 76–81। ডিওআই:10.1038/scientificamerican0793-76।
- Lohani, A.K.; Goel, N.K.; Bhatia K.K.S. (২০০৬)। "Takagi–Sugeno fuzzy inference system for modeling stage–discharge relationship"। Journal of Hydrology। 331 (1): 146–160। ডিওআই:10.1016/j.jhydrol.2006.05.007।
- Lohani, A.K.; Goel, N.K.; Bhatia K.K.S. (২০০৭)। "Deriving stage–discharge–sediment concentration relationships using fuzzy logic"। Hydrological Sciences Journal। 52 (4): 793–807। ডিওআই:10.1623/hysj.52.4.793।
- Lohani, A.K.; Goel, N.K.; Bhatia K.K.S. (২০১১)। "Comparative study of neural network, fuzzy logic and linear transfer function techniques in daily rainfall‐runoff modelling under different input domains"। Hydrological Processes। 25 (2): 175–193। ডিওআই:10.1002/hyp.7831।
- Lohani, A.K.; Goel, N.K.; Bhatia K.K.S. (২০১২)। "Hydrological time series modeling: A comparison between adaptive neuro-fuzzy, neural network and autoregressive techniques"। Journal of Hydrology। 442-443 (6): 23–35। ডিওআই:10.1016/j.jhydrol.2012.03.031।
- Moghaddam, M. J.; Soleymani, M. R.; Farsi, M. A. (২০১৩)। "Sequence planning for stamping operations in progressive dies."। Journal of Intelligent Manufacturing: 1–11।
- Masmoudi, Malek; Haït, Alain (জুলাই ২০১২)। Project scheduling under uncertainty using fuzzy modeling and solving techniques, Engineering Applications of Artificial Intelligence। Elsevier।
- Masmoudi, Malek; Haït, Alain (নভেম্বর ২০১২)। "Fuzzy uncertainty modelling for project planning; application to helicopter maintenance"। International Journal of Production Research। 50 (24)।
- Montagna, F. (২০০১)। "Three complexity problems in quantified fuzzy logic"। Studia Logica। 68 (1): 143–152। আইএসএসএন 0039-3215। ডিওআই:10.1023/A:1011958407631।
- Mundici, Daniele; Cignoli, Roberto; D'Ottaviano, Itala M. L. (১৯৯৯)। Algebraic foundations of many-valued reasoning। Dodrecht: Kluwer Academic। আইএসবিএন 0-7923-6009-5।
- Novák, Vilém (১৯৮৯)। Fuzzy Sets and Their Applications। Bristol: Adam Hilger। আইএসবিএন 0-85274-583-4।
- Novák, Vilém (২০০৫)। "On fuzzy type theory"। Fuzzy Sets and Systems। 149 (2): 235–273। ডিওআই:10.1016/j.fss.2004.03.027।
- Novák, Vilém; Perfilieva, Irina; Močkoř, Jiří (১৯৯৯)। Mathematical principles of fuzzy logic। Dordrecht: Kluwer Academic। আইএসবিএন 0-7923-8595-0।
- Onses, Richard (১৯৯৬)। Second Order Experton: A new Tool for Changing Paradigms in Country Risk Calculation। আইএসবিএন 84-7719-558-7।
- Onses, Richard (১৯৯৪)। Détermination de l´incertitude inhérente aux investissements en Amérique Latine sur la base de la théorie des sous ensembles flous। Barcelona। আইএসবিএন 84-475-0881-1।
- Passino, Kevin M.; Yurkovich, Stephen (১৯৯৮)। Fuzzy control। Boston: Addison-Wesley। আইএসবিএন 0-201-18074-X।
- Pedrycz, Witold; Gomide, Fernando (২০০৭)। Fuzzy systems engineering: Toward Human-Centerd Computing। Hoboken: Wiley-Interscience। আইএসবিএন 978-0-471-78857-7।
- Pu, Pao Ming; Liu, Ying Ming (১৯৮০)। "Fuzzy topology. I. Neighborhood structure of a fuzzy point and Moore-Smith convergence"। Journal of Mathematical Analysis and Applications। 76 (2): 571–599। আইএসএসএন 0022-247X। ডিওআই:10.1016/0022-247X(80)90048-7।
- Sahoo, Bhabagrahi; Lohani, A.K.; Sahu, Rohit K. (২০০৬)। "Fuzzy multiobjective and linear programming based management models for optimal land-water-crop system planning"। Water resources management,Springer Netherlands। 20 (1): 931–948। ডিওআই:10.1007/s11269-005-9015-x।
- Santos, Eugene S. (১৯৭০)। "Fuzzy Algorithms"। Information and Control। 17 (4): 326–339। ডিওআই:10.1016/S0019-9958(70)80032-8।
- Scarpellini, Bruno (১৯৬২)। "Die Nichaxiomatisierbarkeit des unendlichwertigen Prädikatenkalküls von Łukasiewicz"। Journal of Symbolic Logic। Association for Symbolic Logic। 27 (2): 159–170। আইএসএসএন 0022-4812। জেস্টোর 2964111। ডিওআই:10.2307/2964111।
- Seising, Rudolf (২০০৭)। The Fuzzification of Systems. The Genesis of Fuzzy Set Theory and Its Initial Applications -- Developments up to the 1970s। Springer-Verlag। আইএসবিএন 978-3-540-71795-9।
- Steeb, Willi-Hans (২০০৮)। The Nonlinear Workbook: Chaos, Fractals, Cellular Automata, Neural Networks, Genetic Algorithms, Gene Expression Programming, Support Vector Machine, Wavelets, Hidden Markov Models, Fuzzy Logic with C++, Java and SymbolicC++ Programs: 4edition। World Scientific। আইএসবিএন 981-281-852-9।
- Tsitolovsky, Lev; Sandler, Uziel (২০০৮)। Neural Cell Behavior and Fuzzy Logic। Springer। আইএসবিএন 978-0-387-09542-4।
- Wiedermann, J. (২০০৪)। "Characterizing the super-Turing computing power and efficiency of classical fuzzy Turing machines"। Theor. Comput. Sci.। 317 (1–3): 61–69। ডিওআই:10.1016/j.tcs.2003.12.004।
- Yager, Ronald R.; Filev, Dimitar P. (১৯৯৪)। Essentials of fuzzy modeling and control। New York: Wiley। আইএসবিএন 0-471-01761-2।
- Van Pelt, Miles (২০০৮)। Fuzzy Logic Applied to Daily Life। Seattle, WA: No No No No Press। আইএসবিএন 0-252-16341-9।
- Von Altrock, Constantin (১৯৯৫)। Fuzzy logic and NeuroFuzzy applications explained। Upper Saddle River, NJ: Prentice Hall PTR। আইএসবিএন 0-13-368465-2।
- Wilkinson, R.H. (১৯৬৩)। "A method of generating functions of several variables using analog diode logic"। IEEE Transactions on Electronic Computers। 12 (2): 112–129। ডিওআই:10.1109/PGEC.1963.263419।
- Zadeh, L.A. (১৯৬৮)। "Fuzzy algorithms"। Information and Control। 12 (2): 94–102। আইএসএসএন 0019-9958। ডিওআই:10.1016/S0019-9958(68)90211-8।
- Zadeh, L.A. (১৯৬৫)। "Fuzzy sets"। Information and Control। 8 (3): 338–353। আইএসএসএন 0019-9958। ডিওআই:10.1016/S0019-9958(65)90241-X।
- Zemankova-Leech, M. (১৯৮৩)। "Fuzzy Relational Data Bases"। Ph. D. Dissertation। Florida State University।
- Zimmermann, H. (২০০১)। Fuzzy set theory and its applications। Boston: Kluwer Academic Publishers। আইএসবিএন 0-7923-7435-5।
তথ্যসূত্র[সম্পাদনা]
- ↑ Novák, Vilém, 1951- (১৯৯৯)। Mathematical principles of fuzzy logic। Perfilieva, Irina, 1953-, Močkoř, Jiří.। Boston: Kluwer Academic। আইএসবিএন 0-7923-8595-0। ওসিএলসি 41628257।
- ↑ Cintula, Petr; Fermüller, Christian G.; Noguera, Carles (২০১৭)। Zalta, Edward N., সম্পাদক। The Stanford Encyclopedia of Philosophy (২০১৭ সংস্করণ)। Metaphysics Research Lab, Stanford University।
- ↑ Zadeh, L. A. (১৯৬৫-০৬-০১)। "Fuzzy sets"। Information and Control (ইংরেজি ভাষায়)। 8 (3): 338–353। আইএসএসএন 0019-9958। ডিওআই:10.1016/S0019-9958(65)90241-X।
- ↑ Pelletier, Francis Jeffry (২০০০)। "Metamathematics of fuzzy logic" (পিডিএফ)। Bulletin of Symbolic Logic (ইংরেজি ভাষায়)। 6 (3): 342–346। আইএসএসএন 1079-8986। ডিওআই:10.2307/421060।
