ফুরিয়ে রূপান্তর

সময় অনুযায়ী ফুরিয়ে রূপান্তরের কম্পাঙ্ক

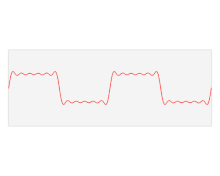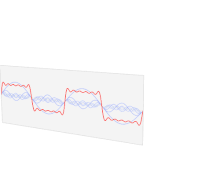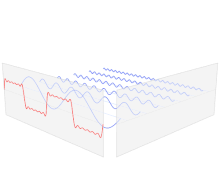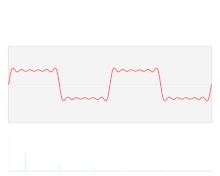
ফুরিয়ে রূপান্তর (ইংরেজি: Fourier transform) এর নাম রাখা হয়েছে বিখ্যাত ফরাসি বিজ্ঞানী ইয়োসেফ ফুরিয়ের নামানুসারে। পদার্থবিজ্ঞান এবং প্রকৌশলে এর অনেক প্রয়োগ রয়েছে। সাধারণভাবে বলা যায়, ফুরিয়ে রূপান্তর সময়ের ফাংশনকে কম্পাঙ্কের ফাংশনে রূপান্তরিত করে, যেখানে কম্পাঙ্কের ফাংশনটিকে সেকেন্ড প্রতি সাইকেল বা রেডিয়ান প্রতি সেকেন্ড এককে প্রকাশ করা হয়। রূপান্তরিত ফাংশনটিকে বলা হয় পুরনোটির ফুরিয়ে রূপান্তর বা কম্পাঙ্ক বর্ণালী (frequency spectrum)। ফুরিয়ে রূপান্তর একটি প্রত্যাবর্তী প্রক্রিয়া, অর্থাৎ ফুরিয়ে প্রত্যাবর্তন উপপাদ্য (Fourier inversion theorem) অনুসারে কম্পাঙ্ক বর্ণালি থেকে সরাসরি আবার সময়ের ফাংশনটি পুনরুদ্ধার করা যায়। সময়ের ফাংশনকে কাল-ডোমেইন রূপ, এবং কম্পাঙ্কের ফাংশনকে কম্পাঙ্ক-ডোমেইন রূপ বলা হয়। এরা আসলে একই ফাংশনের কাল-ডোমেইন ও কম্পাঙ্ক-ডোমেইন রূপ।

অধিকাংশ ক্ষেত্রে ফাংশনটি বাস্তব সংখ্যার হয় এবং তার ফুরিয়ে রূপান্তর করে একটি জটিল সংখ্যাবিশিষ্ট ফাংশন পাওয়া যায়। ফুরিয়ে রূপান্তরটি প্রকৃত ফাংশনের যেকোন একটি কম্পাঙ্ক উপাদানের বিস্তার ও দশা দুটোই প্রকাশ করতে পারে। ফুরিয়ে রূপান্তর দ্বারা অপারেশনটি এবং অপারেশনের পর পাওয়া নতুন জটিল ফাংশন দুটোকেই বোঝানো হয়।

ফাংশনটি যদি পর্যাবৃত্ত হয়, তাহলে ফুরিয়ে রূপান্তরকে সরলীকরণ করা যায়। এক্ষেত্রে ফাংশনটির কিছু জটিল বিস্তার পরিমাপ করলেই ফুরিয়ে রূপান্তর পাওয়া যায়। এই জটিল বিস্তারগুলোকে ফুরিয়ে ধারার সহগ (Fourier series coefficients) বলা হয়। কাল-ডোমেইন সংকেতকে সরাসরি ফুরিয়ে রূপান্তর করলে অবিচ্ছিন্ন ফুরিয়ে রূপান্তর পাওয়া যায়। কিন্তু কম্পিউটারের জায়গা বাচানোর জন্য সাধারণত কাল-ডোমেইন সংকেতকে একটি নির্দিষ্ট কাল অন্তর অন্তর স্যাম্পল করা হয়। স্যাম্পল করার পর ফাংশনটিকে ফুরিয়ে রূপান্তর করলেও আসল অবিচ্ছিন্ন ফুরিয়ে রূপান্তরের একটা সংস্করণ উদ্ধার করা সম্ভব। এটাকে বলা হয় কাল-বিচ্ছিন্ন ফুরিয়ে রূপান্তর (Discrete-time Fourier transform)।

সংজ্ঞা

সমাকলনযোগ্য কোন ফাংশন, $f:\mathbb {R} \to \mathbb {C}$ এর ফুরিয়ে রূপান্তর, ${\hat {f}}$ এর সংজ্ঞা অনেকভাবে দেয়া যায়, অনেকভাবে দেয়ার রীতিও রয়েছে। এই নিবন্ধে যে সংজ্ঞাটি ব্যবহার করা হবে তা হলো:

${\hat {f}}(\xi )=\int _{-\infty }^{\infty }f(x)\ e^{-2\pi ix\xi }\,dx$,   প্রতিটি বাস্তব সংখ্যা ξ এর জন্য.

যেখানে স্বাধীন চলক x সময় বোঝায় যার একক সেকেন্ড, রূপান্তর চলক ξ কম্পাঙ্ক বোঝায় যার একক হার্জ। উপযুক্ত পরিস্থিতি থাকলে বিপরীত ফুরিয়ে রূপান্তরের মাধ্যমে মূল ফাংশনটিকে আবার এভাবে লেখা যায়:

$f(x)=\int _{-\infty }^{\infty }{\hat {f}}(\xi )\ e^{2\pi i\xi x}\,d\xi ,$   প্রতিটি বাস্তব সংখ্যা x এর জন্য

মূল ফাংশনকে তার ফুরিয়ে রূপান্তর থেকে যে পুনরুদ্ধার করা যায় এটাকে বলা হয় ফুরিয়ে প্রত্যাবর্তন উপপাদ্য। ইয়োসেফ ফুরিয়ে তার তাপীয় তত্ত্বের মাধ্যমে এই উপপাদ্য প্রথম প্রণয়ন করেছিলেন (Fourier 1822, পৃ. 525)। অবশ্য আধুনিক দৃষ্টিকোণ থেকে এই উপপাদ্যের প্রকৃত প্রমাণ যাকে বলা যায় তা অনেক পরে এসেছে (Titchmarsh 1948, পৃ. 1)। ƒ and ƒ̂, ফাংশন দুটিকে অনেক সময় ফুরিয়ে সমাকলন জোড় বা ফুরিয়ে রূপান্তর জোড় বলা হয়। ফুরিয়ে রূপান্তর প্রকাশের অন্যান্য নিয়ম আছে যা নিচে আলোচিত হবে। উল্লেখ্য ইউক্লিডীয় স্থানে ফুরিয়ে রূপান্তরের ক্ষেত্রে অনেক সময় x চলক দ্বারা অবস্থান এবং ξ চলক দ্বারা ভরবেগ বোঝানো হয়।

তথ্যসূত্র

• Boashash, B., সম্পাদক (২০০৩), Time-Frequency Signal Analysis and Processing: A Comprehensive Reference, Oxford: Elsevier Science, আইএসবিএন ০-০৮-০৪৪৩৩৫-৪
• Bochner S., K. S. Chandrasekharan (১৯৪৯), Fourier Transforms, Princeton University Press
• Bracewell, R. N. (২০০০), The Fourier Transform and Its Applications (3rd সংস্করণ), Boston: McGraw-Hill, আইএসবিএন ০-০৭-১১৬০৪৩-৪.
• Campbell, George; Foster, Ronald (১৯৪৮), Fourier Integrals for Practical Applications, New York: D. Van Nostrand Company, Inc..
• Duoandikoetxea, Javier (২০০১), Fourier Analysis, American Mathematical Society, আইএসবিএন ০-৮২১৮-২১৭২-৫.
• Dym, H; McKean, H (১৯৮৫), Fourier Series and Integrals, Academic Press, আইএসবিএন ৯৭৮-০-১২-২২৬৪৫১-১.
• Erdélyi, Arthur, সম্পাদক (১৯৫৪), Tables of Integral Transforms, খণ্ড ১, New Your: McGraw-Hill
• Fourier, J. B. Joseph (১৮২২), Théorie Analytique de la Chaleur, Paris: Chez Firmin Didot, père et fils
• Fourier, J. B. Joseph; Freeman, Alexander, translator (১৮৭৮), The Analytical Theory of Heat, The University Press {{citation}}: |first2= প্যারামিটারে সাধারণ নাম রয়েছে (সাহায্য)উদ্ধৃতি শৈলী রক্ষণাবেক্ষণ: একাধিক নাম: লেখকগণের তালিকা (লিঙ্ক)
• Grafakos, Loukas (২০০৪), Classical and Modern Fourier Analysis, Prentice-Hall, আইএসবিএন ০-১৩-০৩৫৩৯৯-X.
• Hewitt, Edwin; Ross, Kenneth A. (১৯৭০), Abstract harmonic analysis. Vol. II: Structure and analysis for compact groups. Analysis on locally compact Abelian groups, Die Grundlehren der mathematischen Wissenschaften, Band 152, Berlin, New York: Springer-Verlag, এমআর 0262773.
• Hörmander, L. (১৯৭৬), Linear Partial Differential Operators, Volume 1, Springer-Verlag, আইএসবিএন ৯৭৮-৩-৫৪০-০০৬৬২-৬.
• James, J.F. (২০১১), A Student's Guide to Fourier Transforms (3rd সংস্করণ), New York: Cambridge University Press, আইএসবিএন ৯৭৮-০-৫২১-১৭৬৮৩-৫.
• Kaiser, Gerald (১৯৯৪), A Friendly Guide to Wavelets, Birkhäuser, আইএসবিএন ০-৮১৭৬-৩৭১১-৭
• Kammler, David (২০০০), A First Course in Fourier Analysis, Prentice Hall, আইএসবিএন ০-১৩-৫৭৮৭৮২-৩
• Katznelson, Yitzhak (১৯৭৬), An introduction to Harmonic Analysis, Dover, আইএসবিএন ০-৪৮৬-৬৩৩৩১-৪
• Knapp, Anthony W. (২০০১), Representation Theory of Semisimple Groups: An Overview Based on Examples, Princeton University Press, আইএসবিএন ৯৭৮-০-৬৯১-০৯০৮৯-৪
• Pinsky, Mark (২০০২), Introduction to Fourier Analysis and Wavelets, Brooks/Cole, আইএসবিএন ০-৫৩৪-৩৭৬৬০-৬, ২৮ মার্চ ২০১৪ তারিখে মূল থেকে আর্কাইভকৃত, সংগ্রহের তারিখ ১৮ ডিসেম্বর ২০১২
• Polyanin, A. D.; Manzhirov, A. V. (১৯৯৮), Handbook of Integral Equations, Boca Raton: CRC Press, আইএসবিএন ০-৮৪৯৩-২৮৭৬-৪.
• Rudin, Walter (১৯৮৭), Real and Complex Analysis (Third সংস্করণ), Singapore: McGraw Hill, আইএসবিএন ০-০৭-১০০২৭৬-৬.
• Rahman, Matiur (২০১১), Applications of Fourier Transforms to Generalized Functions, WIT Press, আইএসবিএন ১৮৪৫৬৪৫৬৪২.
• Stein, Elias; Shakarchi, Rami (২০০৩), Fourier Analysis: An introduction, Princeton University Press, আইএসবিএন ০-৬৯১-১১৩৮৪-X.
• Stein, Elias; Weiss, Guido (১৯৭১), Introduction to Fourier Analysis on Euclidean Spaces, Princeton, N.J.: Princeton University Press, আইএসবিএন ৯৭৮-০-৬৯১-০৮০৭৮-৯.
• Taneja, HC (২০০৮), "Chapter 18: Fourier integrals and Fourier transforms", Advanced Engineering Mathematics:, Volume 2, New Delhi, India: I. K. International Pvt Ltd, আইএসবিএন ৮১৮৯৮৬৬৫৬৭.
• Titchmarsh, E (১৯৪৮), Introduction to the theory of Fourier integrals (2nd সংস্করণ), Oxford University: Clarendon Press (১৯৮৬ তারিখে প্রকাশিত), আইএসবিএন ৯৭৮-০-৮২৮৪-০৩২৪-৫ {{citation}}: আইএসবিএন / তারিখের অসামঞ্জস্যতা (সাহায্য).
• Wilson, R. G. (১৯৯৫), Fourier Series and Optical Transform Techniques in Contemporary Optics, New York: Wiley, আইএসবিএন ০-৪৭১-৩০৩৫৭-৭.
• Yosida, K. (১৯৬৮), Functional Analysis, Springer-Verlag, আইএসবিএন ৩-৫৪০-৫৮৬৫৪-৭.