নোডাল অ্যানালাইসিস

বৈদ্যুতিক বর্তনীর বিশ্লেষণে আমরা নোডাল অ্যানালাইসিস , নোডাল ভোল্টেজ অ্যানালাইসিস বা ব্রাঞ্চ কারেন্ট মেথড ব্যবহার করি একটি বৈদ্যুতিক বর্তনীতে ২টি নোডের মাঝের বিভব পার্থক্য নির্ণয় করার জন্য ।
কার্শফের সূত্র ব্যবহার করে যে কেউ একটি বর্তনী বিশ্লেষণ করতে পারে কারসোফের বিদ্যুৎ সংক্রান্ত সূত্র ব্যবহার করে অথবা মেশ বিশ্লেষণের মাধ্যমে যেখানে আমরা কারসোফের বিভব সংক্রান্ত সূত্র ব্যবহার করব। নোডাল বিশ্লেষণে আমরা প্রতিটি নোডের জন্য একটি করে সমীকরণ বের করব যেখানে প্রতিটি শাখার বিদ্যুতের যোগের মান শুন্য হবে যা ঐ নোডের দিক থেকে আসছে। শাখার বিদ্যুতে সমীকরণ আসলে লেখা হবে বর্তনীর নোড বিভবের মাধ্যমে।একটি রোধের জন্য Iশাখা = Vশাখা * G, যেখানে G (=1/R) হলো রোধের অ্যাডমিটেন্স।
নোডের বিশ্লেষণ সম্ভব যখন প্রত্যেকটি বর্তনীর উপাদানের একটি অভ্যন্তরীণ সম্পর্ক থাকবে অ্যাডমিটেন্সের সাথে।নোডাল অ্যানালাইসিস একটা পূর্ণাঙ্গ সেটের সমীকরণ প্রকাশ করে যা হাত দিয়ে সমাধান করা যায় যদি ছোট আকারের হয় বা তাড়াতাড়ি সমাধান করা যায় লিনিয়ার অ্যালযেব্রা ব্যবহার করে কম্পিউটারের সাহায্যে। একটা নিবিড় মাধ্যম দাঁড় করায় নোডাল অ্যানালাইসিসি সেজন্য অনেক বৈদ্যুতিক বর্তনীর সিমুলেশন প্রোগামে যেমন স্পাইসে নোডাল অ্যানালাইসিস মূল ভিত্তি হিসেবে ব্যবহার করা হয়। যখন নোডাল অ্যানালাইসিসের সরল উদাহরণগুলো লিনিয়ার উপাদানের দিকে নির্দেশ করে, তখন নিউটনের মেথড ব্যবহার করে বর্তনীর বেশি জটিল নন লিনিয়ার সমস্যার সমাধান করা যায়।
পদ্ধতি[সম্পাদনা]
- প্রথমে বর্তনীতে নোড বা সংযোগ স্থলগুলো চিহ্নিত করতে হবে।
- একটা নোডকে রেফারেন্স নোড হিসেবে নির্বাচিত করতে হবে।এই নির্বাচন ফলাফলকে প্রভাবিত করবে না, এটা একটা রীতি মাত্র। বেশি করে নোড নির্বাচন করলে বিশ্লেষণটা সহজ হবে।
- প্রত্যেকটা নোডের জন্য একটা চলক নির্ধারণ করতে হবে যার বিভবটা অজানা। যদি বিভবটা জানা থাকে তবে চলক নির্ধারণের প্রয়োজন নেই।
- প্রত্যেকটা অজানা বিভবের জন্য একটা সমীকরণ বের করতে হবে কারসোফের বৈদ্যুতিক সূত্র ব্যবহার করে।আসলে নোড থেকে বের হওয়া সমস্ত বিদ্যুতের যোগের মান শূণ্যের সমান হবে।
- যদি বিভব উৎস থাকে ২টি অজানা বিভবের মাঝে তবে ২টি নোডকে একটি হিসেবে চিহ্ণিত করতে হবে সুপারনোড হিসেবে।২টি নোডের বিদ্যুতের সমীকরণ হবে একটা এবং বিভবের জন্য একটা নতুন সূত্র গঠিত হবে।
- সমাধান করতে হবে সমীকরণগুলোর প্রত্যেকটা অজানা বিভবের জন্য।
উদাহরণ[সম্পাদনা]
সাধারণ ঘটনা[সম্পাদনা]

শুধু মাত্র একটি অজানা ভোল্টেজ হলো V1। এখানে তিনটি সংযোগ থাকে নোডের সাথে এবং তিনটি বিদ্যুৎ থাকে । বিদ্যুতের দিকটকে ধরা হয় নোডের বাইরের দিকে।
- বিদ্যুতের পরিমাণ রোধ R1-এর ভেতর দিয়ে :(V1 - VS) / R1
- বিদ্যুতের পরিমাণ রোধ R2 -এর ভেতর দিয়ে :(V1 - 0) / R2
- বিদ্যুৎ উৎস IS -এর ভেতর দিয়ে প্রবাহিত বিদ্যুৎ :-IS
কারশোফের বিদ্যুতের সূত্র থেকে আমরা পাইঃ
এই সমীকরণটার সমাধান করা যাবে V1-এর সাপেক্ষে:
সবশেষে অজানা বিভবটার সমাধান করা যাবে অনেক গাণিতিক মানকে প্রতীকে বসিয়ে।অকাজা বিদ্যুতের মান সহজেই জানা যাবে সব বিভবের মান জানার পরে।
সুপারনোড[সম্পাদনা]
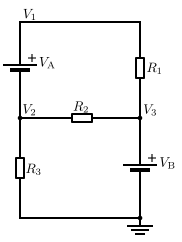
এই বর্তনীতে, আমাদের প্রাথমিকভাবে ২টি অজানা বিভব থাকবে, V1 এবং V2 V3-এ বিভব ইতোমধ্যে জানা আছে যা হলো VB কারণ বিভব উৎসে অন্য ২টি প্রান্তে ভূমির মতো বিভব থাকে। বিভব উৎস VA দিয়ে প্রবাহিত বিদ্যুৎ সরাসরি নির্ণয় করা যায় না।তাই আমরা V1 বা V2-এর জন্য কোন বিদ্যুৎ সমীকরণ নির্ণয় করতে পারি না।যাইহোক, আমরা জানি যে মোট বিদ্যুৎ এই দুইটা নোডের শূণ্য। এই ২টি নোডের সমাবেশকে সুপারনোড কৌশল বলা হয়ে থাকে এবং একটা অতিরিক্ত সমীকরণ দরকার হয়: V1 = V2 + VA
এই বর্তনীর জন্য পূর্ণাঙ্গ সমীকরণের সেট নিম্নে দেওয়া হলো:
প্রতিস্থাপন করে V1কে প্রথম সমীকরণে এবং V2-এর সাপেক্ষে এর সমাধান করে আমরা পাই:





