তরঙ্গ দৈর্ঘ্য

একটি সাইন তরঙ্গ এবং λ এর তরঙ্গদৈর্ঘ্য একই।দশা (ফেজ) দিয়ে যেকোনো দুটি বিন্দুর মধ্যে পরিমাপ করা যায়

পদার্থবিজ্ঞানে তরঙ্গ সঞ্চালনকারী কোনো কম্পনশীল কণার একটি পূর্ণ কম্পন সম্পন্ন হতে যে সময় লাগে সেই সময়ে তরঙ্গ যে দূরত্ব অতিক্রম করে তাকে তরঙ্গদৈর্ঘ্য বলে। এটি তরঙ্গের একই ফেজ এর পরপর সংশ্লিষ্ট বিন্দুর মধ্যে দূরত্ব, যেমন দুটি সংলগ্ন ক্রেস্ট, ট্রফ বা শূন্য ক্রসিং উভয়ই ট্রাভেলিং তরঙ্গের একটি বৈশিষ্ট্য এবং স্থায়ী তরঙ্গ, সেইসাথে অন্যান্য স্থানিক তরঙ্গের একটি নিদর্শন। তরঙ্গদৈর্ঘ্যের বিপরীত দিককে স্থানিক কম্পাঙ্ক বলে। তরঙ্গদৈর্ঘ্য সাধারণত গ্রীক অক্ষর ল্যাম্বদা (λ) দ্বারা মনোনীত হয়। তরঙ্গদৈর্ঘ্য শব্দটি কখনও কখনও মড্যুলেটেড তরঙ্গ এবং বিভিন্ন সাইনোসয়েডের হস্তক্ষেপ দ্বারা গঠিত মডুলেটেড তরঙ্গ বা তরঙ্গের সাইনোসয়েডাল খামেও প্রয়োগ করা হয়। একটি স্থির তরঙ্গ, গতিতে চলমান একটি সাইনোসয়েডাল তরঙ্গকে অনুমান করে, তরঙ্গদৈর্ঘ্য ও তরঙ্গের কম্পাঙ্ক পরস্পর ব্যাস্তানুপাতিক। উচ্চতর কম্পাঙ্কবিশিষ্ট তরঙ্গগুলির ছোট তরঙ্গদৈর্ঘ্য থাকে এবং নিম্ন কম্পাঙ্কবিশিষ্ট তরঙ্গগুলির দীর্ঘতর তরঙ্গদৈর্ঘ্য থাকে।

যে মাধ্যম দিয়ে তরঙ্গ চলাচল করে, সেই মাধ্যমের উপর তরঙ্গদৈর্ঘ্য নির্ভর করে। (উদাহরণস্বরূপ, ভ্যাকুয়াম, বায়ু বা জল)। তরঙ্গের উদাহরণ হল শব্দ তরঙ্গ, আলোকতরঙ্গ, জলতরঙ্গ এবং পর্যায়ক্রমিক বৈদ্যুতিক তরঙ্গ(যা একটি কন্ডাক্টর)। একটি শব্দ তরঙ্গ বায়ুর একটি পরিবর্তনের ফলে চাপ, আলো এবং অন্যান্য ইলেক্ট্রোম্যাগনেটিক রেডিয়েশন এবং চৌম্বক ক্ষেত্র পরিবর্তিত হয়। জলের তরঙ্গ হল জলের পৃষ্ঠের উচ্চতার তারতম্য। একটি স্ফটিক জালির কম্পন এ, পারমাণবিক অবস্থান পরিবর্তিত হয়।

তরঙ্গদৈর্ঘ্য বা কম্পাঙ্কের পরিসরকে বর্ণালী বলা হয়।বর্ণালী নামের উৎপত্তি দৃশ্যমান আলোর বর্ণালী থেকে। এখন সমগ্র ইলেক্ট্রোম্যাগনেটিক স্পেকট্রাম প্রয়োগ এর পাশাপাশি একটি শব্দ বর্ণালী বা কম্পন বর্ণালী প্রয়োগ করা যেতে পারে।

সাইনুসয়েডাল তরঙ্গ

রৈখিক মাধ্যমে, সাইনোসয়েডাল তরঙ্গের উপাদানগুলি স্বাধীন প্রচারের পরিপ্রেক্ষিতে যে কোনও তরঙ্গ প্যাটার্ন বর্ণনা করতে পারে। একটি সাইনোসয়েডাল তরঙ্গরূপের তরঙ্গদৈর্ঘ্য v ধ্রুব গতিতে চলাচল করে।

$\lambda ={\frac {v}{f}}\,\,,$

এখানে v কে তরঙ্গের পর্যায় গতি (ফেজ বেগ]] বলা হয় এবং f হল তরঙ্গের কম্পাঙ্ক। একটি বিচ্ছুরণ মাধ্যম-এ, ফেজ গতি নিজেই তরঙ্গের কম্পাঙ্কের উপর নির্ভর করে।

ইলেক্ট্রোম্যাগনেটিক রেডিয়েশন—যেমন আলোর ক্ষেত্রে—মুক্ত স্থানে, ফেজের গতি হল আলোর গতি, প্রায় ৩×১৯^৮  মাইক্রোসফট. এইভাবে একটি ১০০ মেগাহার্টজ ইলেক্ট্রোম্যাগনেটিক (রেডিও) তরঙ্গের তরঙ্গদৈর্ঘ্য প্রায়: ৩×১০^৮ m/s ১০^৮ Hz = ৩ মিটার দ্বারা ভাগ। দৃশ্যমান আলোর তরঙ্গদৈর্ঘ্য গভীর লাল থেকে, মোটামুটি ৭০০ ন্যানোমিটার )।

বাতাসে শব্দ তরঙ্গ এর জন্য, শব্দের গতি হল ৩৪৩ m/s (রুমের তাপমাত্রা এবং বায়ুমণ্ডলীয় চাপ)। মানুষের কানে শ্রবণযোগ্য শব্দ ফ্রিকোয়েন্সিগুলির তরঙ্গদৈর্ঘ্য (২০ Hz–২০ kHz) এইভাবে যথাক্রমে প্রায় ১৭ মি এবং ১৭ মিমি এর মধ্যে . কিছুটা উচ্চতর ফ্রিকোয়েন্সিগুলি ব্যাট দ্বারা ব্যবহৃত হয় যাতে তারা ১৭ মিমি থেকে ছোট লক্ষ্যগুলি সমাধান করতে পারে। শ্রবণযোগ্য শব্দের তরঙ্গদৈর্ঘ্য দৃশ্যমান আলোর চেয়ে অনেক বেশি।

Sinusoidal standing waves in a box that constrains the end points to be nodes will have an integer number of half wavelengths fitting in the box.

A standing wave (black) depicted as the sum of two propagating waves traveling in opposite directions (red and blue)

Standing waves

A standing wave is an undulatory motion that stays in one place. A sinusoidal standing wave includes stationary points of no motion, called nodes, and the wavelength is twice the distance between nodes.

The upper figure shows three standing waves in a box. The walls of the box are considered to require the wave to have nodes at the walls of the box (an example of boundary conditions) determining which wavelengths are allowed. For example, for an electromagnetic wave, if the box has ideal metal walls, the condition for nodes at the walls results because the metal walls cannot support a tangential electric field, forcing the wave to have zero amplitude at the wall.

The stationary wave can be viewed as the sum of two traveling sinusoidal waves of oppositely directed velocities. Consequently, wavelength, period, and wave velocity are related just as for a traveling wave. For example, the speed of light can be determined from observation of standing waves in a metal box containing an ideal vacuum.

Mathematical representation

Traveling sinusoidal waves are often represented mathematically in terms of their velocity v (in the x direction), frequency f and wavelength λ as:

$y(x,\ t)=A\cos \left(2\pi \left({\frac {x}{\lambda }}-ft\right)\right)=A\cos \left({\frac {2\pi }{\lambda }}(x-vt)\right)$

where y is the value of the wave at any position x and time t, and A is the amplitude of the wave. They are also commonly expressed in terms of wavenumber k (2π times the reciprocal of wavelength) and angular frequency ω (2π times the frequency) as:

$y(x,\ t)=A\cos \left(kx-\omega t\right)=A\cos \left(k(x-vt)\right)$

in which wavelength and wavenumber are related to velocity and frequency as:

$k={\frac {2\pi }{\lambda }}={\frac {2\pi f}{v}}={\frac {\omega }{v}},$

or

$\lambda ={\frac {2\pi }{k}}={\frac {2\pi v}{\omega }}={\frac {v}{f}}.$

In the second form given above, the phase (kx − ωt) is often generalized to (k•r − ωt), by replacing the wavenumber k with a wave vector that specifies the direction and wavenumber of a plane wave in 3-space, parameterized by position vector r. In that case, the wavenumber k, the magnitude of k, is still in the same relationship with wavelength as shown above, with v being interpreted as scalar speed in the direction of the wave vector. The first form, using reciprocal wavelength in the phase, does not generalize as easily to a wave in an arbitrary direction.

Generalizations to sinusoids of other phases, and to complex exponentials, are also common; see plane wave. The typical convention of using the cosine phase instead of the sine phase when describing a wave is based on the fact that the cosine is the real part of the complex exponential in the wave

$Ae^{i\left(kx-\omega t\right)}.$

General media

Wavelength is decreased in a medium with slower propagation.

Refraction: upon entering a medium where its speed is lower, the wave changes direction.

Separation of colors by a prism (click for animation)

The speed of a wave depends upon the medium in which it propagates. In particular, the speed of light in a medium is less than in vacuum, which means that the same frequency will correspond to a shorter wavelength in the medium than in vacuum, as shown in the figure at right.

This change in speed upon entering a medium causes refraction, or a change in direction of waves that encounter the interface between media at an angle. For electromagnetic waves, this change in the angle of propagation is governed by Snell's law.

The wave velocity in one medium not only may differ from that in another, but the velocity typically varies with wavelength. As a result, the change in direction upon entering a different medium changes with the wavelength of the wave.

For electromagnetic waves the speed in a medium is governed by its refractive index according to

$v={\frac {c}{n(\lambda _{0})}},$

where c is the speed of light in vacuum and n(λ₀) is the refractive index of the medium at wavelength λ₀, where the latter is measured in vacuum rather than in the medium. The corresponding wavelength in the medium is

$\lambda ={\frac {\lambda _{0}}{n(\lambda _{0})}}.$

When wavelengths of electromagnetic radiation are quoted, the wavelength in vacuum usually is intended unless the wavelength is specifically identified as the wavelength in some other medium. In acoustics, where a medium is essential for the waves to exist, the wavelength value is given for a specified medium.

The variation in speed of light with wavelength is known as dispersion, and is also responsible for the familiar phenomenon in which light is separated into component colors by a prism. Separation occurs when the refractive index inside the prism varies with wavelength, so different wavelengths propagate at different speeds inside the prism, causing them to refract at different angles. The mathematical relationship that describes how the speed of light within a medium varies with wavelength is known as a dispersion relation.

Nonuniform media

Various local wavelengths on a crest-to-crest basis in an ocean wave approaching shore

Wavelength can be a useful concept even if the wave is not periodic in space. For example, in an ocean wave approaching shore, shown in the figure, the incoming wave undulates with a varying local wavelength that depends in part on the depth of the sea floor compared to the wave height. The analysis of the wave can be based upon comparison of the local wavelength with the local water depth.

A sinusoidal wave travelling in a nonuniform medium, with loss

Waves that are sinusoidal in time but propagate through a medium whose properties vary with position (an inhomogeneous medium) may propagate at a velocity that varies with position, and as a result may not be sinusoidal in space. The figure at right shows an example. As the wave slows down, the wavelength gets shorter and the amplitude increases; after a place of maximum response, the short wavelength is associated with a high loss and the wave dies out.

The analysis of differential equations of such systems is often done approximately, using the WKB method (also known as the Liouville–Green method). The method integrates phase through space using a local wavenumber, which can be interpreted as indicating a "local wavelength" of the solution as a function of time and space. This method treats the system locally as if it were uniform with the local properties; in particular, the local wave velocity associated with a frequency is the only thing needed to estimate the corresponding local wavenumber or wavelength. In addition, the method computes a slowly changing amplitude to satisfy other constraints of the equations or of the physical system, such as for conservation of energy in the wave.

Crystals

A wave on a line of atoms can be interpreted according to a variety of wavelengths.

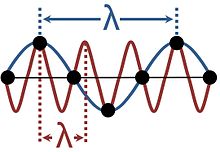
Waves in crystalline solids are not continuous, because they are composed of vibrations of discrete particles arranged in a regular lattice. This produces aliasing because the same vibration can be considered to have a variety of different wavelengths, as shown in the figure. Descriptions using more than one of these wavelengths are redundant; it is conventional to choose the longest wavelength that fits the phenomenon. The range of wavelengths sufficient to provide a description of all possible waves in a crystalline medium corresponds to the wave vectors confined to the Brillouin zone.

This indeterminacy in wavelength in solids is important in the analysis of wave phenomena such as energy bands and lattice vibrations. It is mathematically equivalent to the aliasing of a signal that is sampled at discrete intervals.