স্তরিত নমুনায়ন

স্ট্র্যাটিফাইড র‍্যান্ডমস্যাম্পলিং

পরিসংখ্যানে স্তরিত নমুনায়ন সেইসব তথ্যবিশ্ব থেকে নমুনা সংগ্রহ করার প্রক্রিয়া যাদেরকে কয়েকটি উপ-তথ্যবিশ্বে ভাগ (বিভাজন) করা সম্ভব।

স্তরিত নমুনায়নের উদাহরণ

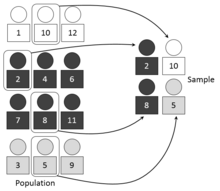
জরিপ করার সময় তথ্যবিশ্বের (population) ভেতরকার উপ-তথ্যবিশ্বগুলি ভিন্ন ভিন্ন বৈশিষ্ট্যের (উপাদান সংখ্যা, গড় ইত্যাদি) হলে প্রত্যেক সাব-পপুলেশন (স্তর) থেকে আলাদাভাবে নমুনা নেওয়া সুবিধাজনক। নমুনা নেওয়ার আগে পপুলেশনকে একজাতীয় উপদলে ভাগ করার প্রক্রিয়া হল স্তরায়ন। স্তরগুলি তথ্যবিশ্বের বিভাজন নির্দেশ করে। একে সম্মিলিতভাবে সম্পূর্ণ এবং বর্জনশীল হতে হবে। অর্থাৎ, পপুলেশনের প্রত্যেক উপাদান একটি এবং কেবল একটি স্ট্র্যাটামেরই অংশ হতে পারে। এরপর প্রত্যেক স্ট্র্যাটামে সিম্পল র‍্যান্ডম স্যাম্পলিং প্রয়োগ করা হয়। এর উদ্দেশ্য হল স্যাম্পলিং ত্রুটি কমিয়ে নমুনাকে আরও নিঁখুত করা। এটা weighted mean নির্ণয় করে যার বিচ্যুতি সিম্পল র‍্যান্ডম স্যাম্পলিংএর গাণিতিক গড়ের চেয়ে কম।

পরিগণনামূলক পরিসংখ্যানে স্ট্র্যাটিফাইড স্যাম্পলিং হল বিচ্যুতি হ্রাস করার উপায় কিন্তু জানা পপুলেশন থেকে পরিসংখ্যান নির্ণয় করতে মন্টে কার্লো পদ্ধতিগুলো ব্যবহৃত হয়।

ধরা যাক আমরা একটি নির্বাচনে প্রত্যেক প্রার্থীর গড় ভোট অনুমান করতে চাই। আরও ধরে নেয়া যাক যে দেশটিতে তিনটি শহর আছে যার মধ্যে  A শহরে ১ মিলিয়ন কারখানা শ্রমিক, B শহরে ২ মিলিয়ন অফিসকর্মী এবং C শহরে ৩ মিলিয়ন অবসরপ্রাপ্ত ব্যক্তি রয়েছেন। আমরা চাইলে সমগ্র পপুলেশন থেকে ৬০ জনের র‍্যান্ডম স্যাম্পল নিতে পারি কিন্তু এক্ষেত্রে প্রাপ্ত নমুনা শহরগুলোর সাথে সঙ্গতিপূর্ণ না হওয়ার আশঙ্কা রয়েছে। তাহলে নমুনাটি হবে পক্ষপাতদুষ্ট যা হিসাবে উল্লেখযোগ্য ত্রুটি ঘটাতে পারে। এর পরিবর্তে যদি আমরা শহর A, B এবং C থেকে যথাক্রমে ১০, ২০ এবং ৩০ জনের র‍্যান্ডম স্যাম্পল নিই, তাহলে আমরা একই আকারের নমুনার জন্য কম ত্রুটিপূর্ণ হিসাব পাব। এই পদ্ধতি সাধারণত তখন ব্যবহার করা হয় যখন পপুলেশনকে সমজাতীয় দলে বিভক্ত করা যায় না।

স্ট্র্যাটিফাইড স্যাম্পলিং কৌশল

• প্রোপোরশনেট অ্যালোকেশন (সমানুপাতিক বরাদ্দ) প্রত্যেক স্ট্র্যাটার নমুনা ভগ্নাংশ ব্যবহার করে যা মোট পপুলেশনের সমানুপাতিক। উদাহরণস্বরুপ, যদি পপুলেশন মোট n জন বিশিষ্ট হয় যার মধ্যে m জন পুরুষ এবং f জন মহিলা (যেখানে m+f=n), তাহলে নমুনাদ্বয়ের আপেক্ষিক আকার এই প্রোপোরশনকে নির্দেশ করে। ধরা যাক, N সংখ্যক উপাদানের পপুলেশনকে Lটি স্ট্র্যাটায় ভাগ করে প্রতি স্ট্র্যাটাম থেকে n_h টি করে মোট n টি নমুনা নেওয়া হবে। যখন প্রতি স্ট্র্যাটামের পপুলেশন N_h । প্রোপোরশনেট অ্যালোকেশন পদ্ধতি অনুয়ায়ী প্রত্যেক স্ট্র্যাটাম থেকে নিম্নোক্ত পদ্ধতিতে নমুনা সংগ্রহ করা হয়ঃ

$n_{h}\propto N_{h}\Rrightarrow n_{h}=kN_{h}\Rrightarrow k=n_{h}/N_{h}$

$\therefore \sum _{h=0}^{L}n_{h}=k\sum _{h=0}^{L}N_{h}\Rrightarrow n=kN\Rrightarrow n=(n_{h}/N_{h})N\Rrightarrow n_{h}=(N_{h}/N)n$

• অপটিমাম অ্যালোকেশন (বা অসম বরাদ্দ)- প্রত্যেক  স্ট্র্যাটার নমুনা ভগ্নাংশ প্রোপোরশন (উপরের মতো) এবং রাশির স্ট্যান্ডার্ড ডেভিয়েশন (পরিমিত ব্যবধান) উভয়েরই সমানুপাতিক। সর্বাধিক বিচ্যুতির স্ট্র্যাটা থেকে বেশি নমুনা সংগ্রহ করা হয় যাতে সম্ভাব্য সর্বনিম্ন স্যাম্পলিং ভ্যারিয়েন্স পাওয়া যায়। $n_{h}\propto N_{h}S_{h}\Rrightarrow n_{h}=kN_{h}S_{h}$ $\therefore \sum _{h=0}^{L}n_{h}=k\sum _{h=0}^{L}(N_{h}S_{h})$ $\Rrightarrow n=\left({\frac {n_{h}}{N_{h}S_{h}}}\right)\sum _{h=0}^{L}(N_{h}S_{h})$ $\Rrightarrow n_{h}=\left({\frac {N_{h}S_{h}n}{\sum _{h=0}^{L}(N_{h}S_{h})}}\right)$
• ইকুয়াল ডিস্ট্রিবিউশন(সমবন্টণ)- এই পদ্ধতিতে সকল স্ট্র্যাটাম থেকে সমান সংখ্যক নমুনা নেয়া হয়। উদাহরণস্বরূপ, কোনো ক্লাসে সমপরিমাণে ছাত্র এবং ছাত্রী থাকলে পপুলেশনকে দুটি স্ট্র্যাটামে ভাগ করে এরপর সমান সংখ্যক নমুনা নেয়া যেতে পারে। $\therefore n_{h}=n/h$

স্ট্র্যাটিফাইড স্যাম্পলিং এর একটি বাস্তব উদাহরণ হল রাজনৈতিক সমীক্ষা । জরিপে অংশগ্রহণকারীদের মাধ্যমে পপুলেশনের বৈচিত্র্য তুলে ধরতে চাইলে গবেষক মূলত বিভিন্ন জাতি বা ধর্মীয় সংখ্যালঘু গোষ্ঠীর মানুষদেরকে সমগ্র পপুলেশনে তাদের অনুপাতের ভিত্তিতে অন্তর্ভুক্ত করবেন। এজন্যই স্ট্র্যাটিফাইড স্যাম্পলিং পদ্ধতির জরিপ সিম্পল র‍্যান্ডম বা সিস্টেমেটিক স্যাম্পলিং পদ্ধতির চেয়ে নির্ভুলভাবে পপুলেশনের প্রতিনিধিত্ব করে।

সুবিধা

সিম্পল র‍্যান্ডম স্যাম্পলিং এর পরিবর্তে স্ট্র্যাটিফাইড স্যাম্পলিং ব্যবহারের কারণগুলো হলঃ

1. স্ট্র্যাটার উপাদানের পরিমিত ব্যবধান অল্প হলে স্ট্র্যাটিফিকেশন পদ্ধতিতে হিসাবের ত্রুটি অপেক্ষাকৃত কম হয়।
2. অনেক ক্ষেত্রে পপুলেশনকে স্ট্র্যাটায় ভাগ করে নিলে হিসাব-নিকাশ সহজে পরিচালনা করা সম্ভব হয়, আবার খরচও কম হয়।
3. অনেক সময় পপুলেশনের মধ্যকার গ্রুপের প্যারামিটারগুলো জানার প্রয়োজন হতে পারে।

কোনো অঞ্চলে একেক জায়গায় জনসংখ্যার ঘনত্ব একেক রকম হলে স্ট্র্যাটিফাইড স্যাম্পলিং পদ্ধতি ব্যবহার করে ঐ অঞ্চলের প্রত্যেক অংশে একই রকম নির্ভুল হিসাব নিশ্চিত করা যাবে। উদাহরণস্বরূপ, অন্টারিও প্রদেশজুড়ে একটি জরিপ কম জনবহুল উত্তর অংশ থেকে তুলনামূলক বেশি নমুনা নিয়ে নিতে পারে। কেননা উত্তর এবং দক্ষিণের মধ্যে জনসংখ্যার এতোই তারতম্য রয়েছে যে এরকম প্রদেশজুড়ে নমুনা নিলে মূলত কেবল উত্তরের তথ্য সংগ্রহ করা হবে।

অসুবিধা

যখন সামগ্রিকভাবে (exhaustively) পপুলেশনকে আলাদা-আলাদা দলে বিভক্ত করা যায় না সেসব ক্ষেত্রে স্ট্র্যাটিফাইড স্যাম্পলিং কার্যকর নয়। নমুনা আকারকে সাবপগ্রুপের বিস্তৃতির সমানুপাতিক (অথবা যেসকল ক্ষেত্রে ভেদাঙ্ক সমান নয় সেক্ষেত্রে ভেদাঙ্কের সমানুপাতিক) না করে যদি সাবগ্রুপে প্রাপ্ত তথ্য সংখ্যার সমানুপাতিক করা হয় তাহলে ভুল হতে পারে। সাবগ্রুপগুলোর ভেদাঙ্কে সামান্য পার্থক্য থাকলে স্ট্র্যাটিফাইড স্যাম্পলিং করে প্রত্যেক সাবগ্রুপের ডাটাকে সমান গুরুত্বসহকারে বিবেচনা করা যায়। ভেদাঙ্কে উল্লেখযোগ্য পার্থক্য থাকলে এবং ভেদাঙ্কের ভিত্তিতে স্ট্র্যাটিফাই করতে হলে সাবগ্রুপের আকারের সমানুপাতিক ধরে নমুনা আকার নেওয়া সম্ভব না। গ্রুপের নমুনা উপাদানগুলো গড়, ভেদাঙ্ক এবং খরচের দিক দিয়ে পৃথক হলে সাবগ্রুপ করার একটি উপযুক্ত উপায় হল- "প্রোপোরশনেট অ্যালোকেশন" । অজানা পপুলেশনের জন্য ( যখন পপুলেশনের মধ্যে সাব-পপুলেশনের অনুপাতগুলো অজানা) স্ট্র্যাটিফাইড স্যাম্পলিং শ্রেণিবিন্যাসের মতো বিশ্লেষণজাতীয় কাজের ক্ষেত্রে নেতিবাচক প্রভাব রাখতে পারে। এসব ক্ষেত্রে ডাটা সেটকে তথ্য সংগ্রহের অনিশ্চয়তার বিরুদ্ধে শক্তিশালী করার জন্য মিনিম্যাক্স স্যাম্পলিং অনুপাত ব্যবহার করা যেতে পারে।

পর্যাপ্ত তথ্যের জন্য সাব-স্ট্রাটাগুলোকে একত্রিত করলে সিম্পসনের প্যারাডক্স তৈরী হতে পারে। যেখানে গ্রুপগুলো একত্রিত করার কারণে ভিন্ন গ্রুপের বৈশিষ্ট্য হারিয়ে যেতে পারে এমনকি উল্টেও  যেতে পারে।

গড় এবং স্ট্যান্ডার্ড এরর

স্ট্র্যাটিফাইড র‍্যান্ডম স্যাম্পলিং এর গড় এবং ভেদাঙ্ক :

${\bar {x}}={\frac {1}{N}}\sum _{h=1}^{L}N_{h}{\bar {x_{h}}}$

$s_{\bar {x}}^{2}=\sum _{h=1}^{L}\left({\frac {N_{h}}{N}}\right)^{2}\left({\frac {N_{h}-n_{h}}{N_{h}}}\right){\frac {s_{h}^{2}}{n_{h}}}$

যেখানে,

$L=$ স্তরের (স্ট্র্যাটা) সংখ্যা

$N=$ সমস্ত স্ট্র্যাটার আকারের যোগফল

$N_{h}=$ $h$ স্ট্র্যাটার আকার

${\bar {x_{h}}}=$ $h$ স্ট্র্যাটার নমুনার গড়

$n_{h}=$ $h$ স্ট্র্যাটার পর্যবেক্ষণ সংখ্যা

$s_{h}=$ $h$ স্ট্র্যাটার নমুনার পরিমিত ব্যবধান

মনে রাখতে হবে যে, ( $N_{h}$ - $n_{h}$ ) / ( $N_{h}$ ) বা (1 - $n_{h}$ / $N_{h}$ ) টার্মটি একটি ফাইনাইট পপুলেশন কারেকশন এবং $N_{h}$ কে অবশ্যই "নমুনা ইউনিট" এ প্রকাশ করতে হবে। ফাইনাইট পপুলেশন কারেকশনকে বাদ দিলে :

$s_{\bar {x}}^{2}=\sum _{h=1}^{L}\left({\frac {N_{h}}{N}}\right)^{2}{\frac {s_{h}^{2}}{n_{h}}}$

যেখানে $w_{h}$ = $N_{h}$ / $N$ স্ট্র্যাটামের পপুলেশন ওয়েট $h$ ।

নমুনা আকার বরাদ্দকরণ

সমানুপাতিক বরাদ্দ কৌশলের ক্ষেত্রে স্ট্র্যাটামের আকারের অনুপাত অনুযায়ী সেই স্ট্র্যাটামের স্যাম্পলের আকার নির্ধারণ করা হয়। ধরা যাক, কোনো সংস্থায় নিম্নোক্ত কর্মচারী রয়েছেন:

• পুরুষ, পূর্ণকালীন: ৯০
• পুরুষ, খণ্ডকালীন: ১৮
• মহিলা, পূর্ণকালীন: ৯
• মহিলা, খণ্ডকালীন: ৬৩
• মোট: ১৮০

এবং আমাদের উপর্যুক্ত বিভাজন অনুসারে ৪০ জনের স্ট্র্যাটিফাইড নমুনা সংগ্রহ করতে বলা হয়েছে ।

প্রথম পদক্ষেপটি হল প্রতিটি গ্রুপের শতাংশ গণনা করা।

• % পুরুষ, পূর্ণকালীন = ৯০ ÷ ১৮০ = ৫০%
• % পুরুষ, খণ্ডকালীন = ১৮ ÷ ১৮০ = ১০%
• % মহিলা, পূর্ণকালীন = ৯ ÷ ১৮০ = ৫%
• % মহিলা, খণ্ডকালীন = ৬৩ ÷ ১৮০ = ৩৫%

তাহলে আমাদের ৪০ জনের নমুনা দাঁড়ায়,

• ৫০% (২০ জন) পুরুষ, পূর্ণকালীন।
• ১০% (৪ জন) পুরুষ, খণ্ডকালীন ।
• ৫% (২ জন) মহিলা, পূর্ণকালীন ।
• ৩৫% (১৪ জন) মহিলা, খণ্ডকালীন।

শতকরা হিসাব ছাড়াই নমুনার আকার নির্ণয়ের একটা সহজ উপায় হল প্রত্যেক গ্রুপের আকারকে নমুনার আকার দিয়ে গুণ করে পপুলেশন (সকল কর্মীদের সংখ্যা) দিয়ে ভাগ করা :

• পুরুষ, পূর্ণকালীন = ৯০ × (৪০ ÷ ১৮০) = ২০
• পুরুষ, খণ্ডকালীন = ১৮ × (৪০ ÷ ১৮০) = ৪
• মহিলা, পূর্ণকালীন = ৯ × (৪০ ÷ ১৮০) = ২
• মহিলা, খণ্ডকালীন = ৬৩ × (৪০ ÷ ১৮০) = ১৪

আরো দেখুন

• মতামত গ্রহণ
• পরিসংখ্যানগত মানদণ্ড
• স্ট্র্যাটিফাইড নমুনার আকার
• স্ট্র্যাটিফিকেশন (ক্লিনিকাল ট্রায়াল)

 

আরো পড়ুন

• Särndal, Carl-Erik (২০০৩)। "Stratified Sampling"। Model Assisted Survey Sampling। Springer। পৃষ্ঠা 100–109। আইএসবিএন 0-387-40620-4।