সাপোর্ট-ভেক্টর মেশিন

মেশিন লার্নিংয়ে সাপোর্ট ভেক্টর মেশিন (এসভিএম, অথবা সাপোর্ট-ভেক্টর নেটোয়ার্ক) এক প্রকার সুপারভাইজড লার্নিং মডেল যা উপাত্তসমূহকে বিশ্লেষন করে শ্রেণিবিভাগ করতে এবং উপাত্তসমূহের মধ্যকার রৈখিক প্রতিক্রিয়া নিরূপনে সংশ্লিষ্টতা শিক্ষণ এলগোরিদম (Associated learning algorithm) ব্যবহার করে। একটি অনুশীলন উপাত্তের সেট, যার প্রতিটি উপাদান কোন দুইটি শ্রেণির যেকোন একটির চিহ্নিত সদস্য হলে, সাপোর্ট ভেক্টর মেশিন প্রশিক্ষণ এলগোরিদম সেটটির উপাত্তসমূহের উপর প্রশিক্ষিত হয়ে এমন একটি মডেল তৈরী করবে যা কোন নতুন উপাত্তকে উক্ত দুইটি শ্রেণির যেকোন একটির সদস্য হিসেবে চিহ্নিত করবে। যদিও প্রক্রিয়াটি এসভিএম-কে একটি সম্ভাব্যতাবিহীন রৈখিক দ্বি-শ্রেনীবিভাজক এলগোরিদম হিসেবে প্রতিষ্ঠিত করে তবুও কিছু পদ্ধতি যেমন প্লাট স্কেলিং (Platt scaling) এর মাধ্যমে এসভিএম-কে সম্ভাব্যতাভিত্তিক বিভাজনের ক্ষেত্রেও ব্যবহারযোগ্য করে। একটি এসভিএম মডেল চিহ্নিত প্রশিক্ষণ উপাত্তদেরকে একটি বহুমাত্রিক স্থানে বিন্দু হিসেবে উপস্থাপন করে এমন একটি রেখা বা অধিতল খুজে বের করে যার থেকে দুইটি শ্রেণীর উপাত্তদের মধ্যকার দূরত্ব সর্বোচ্চ হয়। মডেলটি নতুন অচিহ্নিত উপাত্তদের সেই একই স্থানে বিন্দু হিসেবে উপস্থাপন করে পূর্বের খুজে পাওয়া রেখার বা অধিতলের কোন পার্শ্বে বিন্দুটির অবস্থান তার ভিত্তিতে উপাত্তটিকে শ্রেণিবিভাগ করে।

সরলরৈখিক বিভাজনের পাশাপাশি সাপোর্ট ভেক্টর মেশিনে কার্নেল ট্রিক ব্যবহার করে বক্ররৈখিক শ্রেণিবিভাগও করা যায়। কার্নেল ট্রিক ইনপুট উপাত্তসমূহকে এমন একটি উচ্চতর মাত্রার স্থানাংক ব্যবস্থায় নিয়ে যায় যেখানে তাদের রৈখিক বিভাজন করা সম্ভব হয়।

অচিহ্নিত উপাত্তসমূহের ক্ষেত্রে সুপারভাইজড লার্নিং সম্ভবপর নয়। এক্ষেত্রে আনসুপারভাইজড লার্নিং ব্যবহার করতে হয় যেখানে উপাত্তসমূহকে বহুমাত্রিক তলে তাদের ঘনত্বের ভিত্তিতে গুচ্ছবদ্ধ করে তাদের শ্রেনি চিহ্নিত করতে হয়। অচিহ্নিত তথ্য চিহ্নিত করার জন্য সাপোর্ট ভেক্টর মেশিনের পরিসংখ্যান ব্যবহার করে Hava Siegelmann ও Vladimir Vapnik "সাপোর্ট ভেক্টর ক্লাস্টারিং" নামের এলগোরিদম প্রচলন করেছেন।

অনুপ্রেরণা

চিত্রে দেখানো হচ্ছে কীভাবে সাপোর্ট ভেক্টর মেশিন দ্বিমাত্রিক স্থানে একটি দুই শ্রেণিতে বিভাজক অধিতল গ্রহণ করবে। H₁ অধিতল পূর্ণ বিভাজক নয়, H₂ স্বল্প ব্যাবধি পূর্ণ বিভাজক অধিতল এবং H₃ সর্বোচ্চ ব্যাবধি পূর্ণ বিভাজক অধিতল।

মেশিন লার্নিংয়ে উপাত্ত শ্রেণিবিভাগ করা একটি সাধারণ ক্রিয়া। ধরি কিছু উপাত্ত দেওয়া আছে যাদের প্রত্যেকে দুইটি শ্রেণির যেকোন একটির সদস্য এবং লক্ষ্য হলো কোন নতুন উপাত্তকে সঠিকভাবে ওই দুইটি শ্রেণির কোনটির সদস্য তা নিরুপণ করা। সাপোর্ট ভেকটর মেশিনের ক্ষেত্রে, একটি উপাত্তকে দেখা হয় একটি n-মাত্রিক অবস্থান ভেক্টর হিসেবে এবং এমন উপাত্তসমূহের সাপেক্ষে একটি n-মাত্রিক বিভাজক অধিতল খুজে বের করা যায় কিনা তাই দেখা হয়। একে বলে সরলরৈখিক শ্রেণিবিভাগ। যদি এরকম একাধিক বিভাজক অধিতল থাকে তবে এদের মধ্যে যে অধিতলটির থেকে যেকোন শ্রেণীর সবচেয়ে নিকটবর্তি উপাত্তটির দূরত্ব সর্বোচ্চ সেই অধিতলটিই গ্রহণ করা হয়। যদি এমন অধিতল থেকে থাকে তবে তাকে সর্বোচ্চ ব্যাবধি অধিতল বলে এবং যদি কোন শ্রেণিবিভাজক এটিকে ব্যবহার করে তবে তাকে সর্বোচ্চ ব্যাবধি শেণিবিভাজক বলে। সাপোর্ট ভেক্টর মেশিন এরকম একটি সর্বোচ্চ ব্যাবধি শ্রেণিবিভাজক।

সংজ্ঞা

সাপোর্ট ভেক্টর মেশিন বহুমাত্রিক বা অসীমমাত্রিক স্থানে এমন একটি অধিতল বা অধিতলসমূহের সেট তৈরী করে যা শ্রেণিবিভাজনে, রৈখিক প্রতিক্রিয়া নিরূপনে বা অন্যান্য উদ্দেশ্য যেমন অস্বাভাবিক উপাত্ত স্নাক্তকরণের কাজে ব্যবহৃত হয়। সহজজ্ঞানে, অধিতল দ্বারা একটি ভালো বিভাজন সম্পন্ন হবে যদি অধিতলটি থেকে সবচেয়ে নিকটবর্তী প্রশিক্ষণ উপাত্তটির (যেকোন শ্রেণির) দূরত্ব (ফাংশনাল ডিসটেন্স বা সক্রিয় দূরত্ব নামে পরিচিত) সর্বোচ্চ হয়, কারণ এই দূরত্ব যতই বড় হবে ততই শ্রেণিবিভাজকের সর্বজনীনকৃত ভ্রান্তি (generalization error) কম হবে।

কার্নেল মেশিন

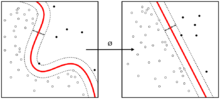
যদিও মূল সমস্যাগুলো সীমিত মাত্রার স্থানের জন্য বর্ণিত, প্রায়শ এমন হয় যে বিভাজনের উপাত্তগুলো সেই মাত্রায় সরলরৈখিকভাবে বিভাজনযোগ্য নয়। এজন্য প্রস্তাব করা হয় যে, মূল সমস্যায় সীমিত মাত্রাগুলোকে উচ্চতর মাত্রায় প্রক্ষেপিত হবে এই অনুমানে যেন সেই উচ্চতর মাত্রায় বিভাজন প্রক্রিয়া সহজতর হয়। গণনা যথাযথ পরিমাণ সংক্ষেপিত রাখার জন্য প্রক্ষেপণ পদ্ধতি এমনভাবে পরিকল্পনা করা হয় যেন ইনপুট উপাত্ত ভেক্টরগুলোর ডট গুণন সহজে পরিমাপ করা যায় এবং উপাত্তগুলোকে সমস্যার সাথে সামঞ্জস্যপূর্ণ কোন পারস্পরিক সদৃশতা পরিমাপক ফাংশন বা কার্নেল ফাংশন $k(x,y)$বেছে নেওয়া হয়। উচ্চতর স্থানে অধিতলগুলোকে কতগুলো বিন্দুর সেট হিসেবে বর্ণনা করা যায়, যে বিন্দুগুলোকে একটি ভেক্টরের সাথে ডট গুণন করলে ধ্রুবক রাশি পাওয়া যায়। অধিতল বর্ণনাকারী ভেক্টরগুলো লম্বভেক্টরের সেট গঠন করে । এই অধিতল বর্ণনাকারী ভেক্টরগুলোকে উপাত্তের ফিচার ভেক্টরগুলোর সাথে যথাযথ প্যারামিটার দ্বারা গুণ করে লিনিয়ার কম্বিনেশন হিসেবে প্রকাশ করা যায়। এই পরামাত্রিক সম্পর্কের সাহায্যে ফিচারস্পেসের বিন্দুগুলোকে অধিতলের মাত্রায় রূপান্তর করা যায়।

ব্যবহার

সাপোর্ট ভেক্টর মেশিন বিভিন্ন বাস্তবধর্মী সমস্যা সমাধানে ব্যবহার করা হয়ঃ

• এসভিএম টেক্সট এবং হাইপারটেক্সট তথ্য শ্রেণিবিভাগে সহায়ক কারণ এটি ব্যবহারে ইন্ডাক্টিভ এবং ট্রান্সডাক্টিভ লার্নিংয়ের ক্ষেত্রে তুলনামূলক কম সংখ্যক চিহ্নিত উপাত্তের প্রয়োজন হয় । কিছু শ্যালো সেমান্টিক পারসিং পদ্ধতি সাপোর্ট ভেক্টর মেশিন ব্যবহার করে।
• ছবির শ্রেণিবিভাগের ক্ষেত্রেও সাপোর্ট ভেক্টর মেশিন ব্যবহার হয়েছে। গবেষণায় দেখা গেছে তিন-চার স্তরের কোয়ারী রিফাইনমেন্ট প্রক্রিয়ার থেকে এসভিএম ভিত্তিক আরো ভালো শ্রেণিবিভাজক রয়েছে। অবশ্য অন্য কোন শ্রেণিবিভাজকের সাপেক্ষে এসভিএমের সক্ষমতা নিশ্চিতভাবে যাচাই হয় নি।