ব্রহ্মগুপ্তের উপপাদ্য

${\overline {BD}}\perp {\overline {AC}},{\overline {EF}}\perp {\overline {BC}}$ $\Rightarrow |{\overline {AF}}|=|{\overline {FD}}|$

কোন চতুর্ভুজের শীর্ষ বিন্দু চারটি একটি বৃত্তের পরিধির উপর অবস্থান করলে চতুর্ভুজটিকে বৃত্তীয় চতুর্ভুজ বলা হয়। আবার চতুর্ভুজ কর্ণদ্বয় পরস্পর লম্ব হলে এটি হবে লম্বকর্ণ চতুর্ভুজ। এখন একটি বৃত্তীয় চতুর্ভুজ লম্বকর্ণ চতুর্ভুজ হলে অর্থাৎ বৃত্তের অন্তস্থ কোন চতুর্ভুজের কর্ণদ্বয় পরস্পরের লম্ব হলে কর্ণদ্বয়ের ছেদবিন্দু থেকে চতুর্ভুজটির যেকোন বাহুর উপর অঙ্কিত লম্বটি সর্বদা ঐ বাহুর বিপরীত বাহুকে সমদ্বিখণ্ডিত করবে। এটিই ব্রহ্মগুপ্তের উপপাদ্য যা প্রাচীন ভারতীয় গণিতবিদ ও জ্যোতির্বিজ্ঞানী ব্রহ্মগুপ্তের (৫৯৮-৬৬৮)নামানুসারে নামকরণ করা হয়েছে।

আরও ভালোভাবে বোঝার জন্য বৃত্তের পরিধিস্থ A, B, C এবং D বিন্দু চারটি বিবেচনা করা যাক যেখানে AC ও BD রেখা দুটি পরস্পরের লম্ব এবং এদের ছেদবিন্দু M দ্বারা সূচিত। M বিন্দুটি থেকে BC রেখাংশের উপর EM লম্বটি টানা হল যা BC কে E বিন্দুতে ছেদ করে। EM এর বর্ধিতাংশ MF টানা যাক যা আবার AD কে F বিন্দুতে ছেদ করে। তাহলে ব্রহ্মগুপ্তের উপপাদ্যের বর্ণনা অনুসারে F হল AD এর মধ্যবিন্দু।

প্রমাণ

ব্রহ্মগুপ্তের উপপাদ্যের প্রমাণ।

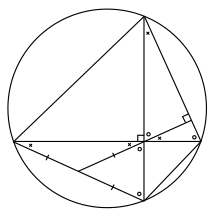
আমাদের প্রমাণ করতে হবে যে, AF = FD । AF এবং FD উভয়ই যে আদতে FM এর সমান আমরা এখন সেটা প্রমাণ করব।

যেহেতু ∠CBD এবং ∠CAD দুটি কোণই একই বৃত্তের অন্তর্লিখিত কোণ এবং উভয়ই একই চাপের উপর অবস্থিত তাই এরা পরস্পর সমান।

∠CBD = ∠CAD - - - - - (i)

যেহেতু BCM সমকোণী ত্রিভুজে কোণ ∠BMC এক সমকোণ সুতরাং

∠CBD + ∠BCM = ১ সমকোণ - - - - - (ii)

একইভাবে MEC ত্রিভুজের ক্ষেত্রেও কোণ ∠MEC এক সমকোণ। সুতরাং

∠CME + ∠BCM = ১ সমকোণ - - - - - (iii)

অতএব (ii) এবং (iii) নং থেকে পাই—

∠CBD + ∠BCM = ∠CME + ∠BCM = ১ সমকোণ

বা, ∠CBD = ∠CME - - - - - (iv)

আবার ∠CME ও ∠AMF পরস্পরের বিপ্রতীপ কোণ হওয়ায় এরা পরস্পরের সমান।

∠CME = ∠AMF - - - - - (v)

সুতরাং (i), (iv) এবং (v) নং সমীকরণ থেকে পাই—

∠CBD = ∠CAD = ∠CME = ∠AMF

বা, ∠CAD = ∠AMF

বা, ∠MAF = ∠AMF

তাহলে দেখা যাচ্ছে যে, AFM ত্রিভুজটি সমদ্বিবাহু। ফলে AF ও FM বাহু দুটি পরস্পর সমান।

AF = FM

একইভাবে দেখানো যায় যে, ∠FDM, ∠BCM, ∠BME এবং ∠DMF কোণ চারটি পরস্পর সমান। ফলে DFM ত্রিভুজটিও সমদ্বিবাহু ত্রিভুজ। যার দরুন FD ও FM বাহু দুটি পরস্পরের সমান।

FD = FM

সুতরাং আমরা পাচ্ছি—

AF = FD = FM

যা ব্রহ্মগুপ্তের উপপাদ্যে বলা হয়েছে।

বহিঃসংযোগ

• Brahmagupta's Theorem at cut-the-knot
• এরিক ডব্লিউ. ওয়াইস্টাইন সম্পাদিত ম্যাথওয়ার্ল্ড থেকে "Brahmagupta's theorem"।
• Amelia Rector's YouTube video