ব্যবহারকারী:Meghmollar2017/খেলাঘর/১

মূল নিবন্ধ: en:Octagon

সুষম অষ্টভুজ
একটি সুষম অষ্টভুজ
প্রকার	সুষম বহুভুজ
প্রান্ত ও ছেদচিহ্ন	৮
শ্লেফলি প্রতীক	{8}, t{4}
কক্সিটার ডায়াগ্রাম
প্রতিসাম্য দল	দ্বিতল (D৮), ২×৮ ক্রম
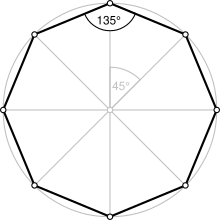
অভ্যন্তরীণ কোণ (ডিগ্রি)	১৩৫°
দ্বৈত বহুভুজ	স্বকীয়
বৈশিষ্ট্যাবলি	উত্তল, পরিবৃত্তীয়, সমবাহু, আইসোগোনাল, আইসোটক্সাল

জ্যামিতিক পরিভাষায় অষ্টভুজ (সংস্কৃত: অষ্টভুজ; “আট বাহু”) হলো আট বাহুবিশিষ্ট বহুভুজ।

একটি সুষম অষ্টভুজ-এর শ্লেফলি প্রতীক {8}। একে ছদ্ম-সমবাহু বিশিষ্ট ভোঁতাপ্রান্তবিশিষ্ট বর্গ t{4} হিসেবে প্রকাশ করা যায়, যা দুই ধরনের প্রান্ত বদল করে। পক্ষান্তরে একটি ভোঁতা-প্রান্তবিশিষ্ট অষ্টভুজ t{8} হলো একটি ষোড়শভুজ {16}। অষ্টভুজের ত্রিমাত্রিক প্রতিরূপ হলো রম্বিকিউবোক্টাহেড্রন। অষ্টভুজকে ভোঁতা-প্রান্তবিশিষ্ট বর্গ বিবেচনা করলে এর প্রতিস্থাপিত প্রান্তগুলো রম্বিকিউবোক্টাহেড্রনের ত্রিভুজাকার তল হিসেবে বিবেচনা করা যায়।

ধর্ম

সবুজ রঙের চতুর্ভুজের কর্ণসমূহের দৈর্ঘ্য সমান এবং একে অপরের ওপর লম্ব

অষ্টভুজের অন্তঃকোণসমূহের সমষ্টি ১০৮০°। যেকোনো বহুভূজের মতো অন্তঃ ও বহিঃকোণের সমষ্টি ৩৬০°।

অষ্টভুজের প্রতিটি বাহুর অন্তঃ ও বহির্পার্শ্বে বাহুর সমান দৈর্ঘ্যের বর্গ অঙ্কন করা হলে, প্রতিটি বিপরীত বাহুর বর্গের কর্ণসমূহের ছেদবিন্দুর সংযোগরেখার মধ্যবিন্দু যে চতুর্ভুজের চারটি শীর্ষবিন্দু নির্দেশ করে, তার কর্ণসমূহ সমান ও সমকোণ উৎপন্ন করে।

প্রদত্ত অষ্টভুজের প্রতিটি বাহুর মধ্যবিন্দু যুক্ত করে মধ্যবিন্দু অষ্টভুজ অঙ্কন করা যায়। যদি মধ্যবিন্দু অষ্টভুজের প্রতিটি বাহুর অভ্যন্তর বা বাইরের দিকে বাহুর সমান দৈর্ঘ্যের বর্গ অঙ্কন করা হয়, তাহলে প্রতি দুই বিপরীত বাহুর বর্গের কর্ণসমূহের ছেদবিন্দুর সংযোগকারী রেখাগুলোর মধ্যবিন্দু একটি বর্গের শীর্ষবিন্দু নির্দেশ করে।

সমবাহুতা

একটি সুষম অষ্টভুজ হলো আটটি সমান বাহু ও অন্তঃকোণবিশিষ্ট আবদ্ধ কাঠামো। এটি আট মাত্রার দর্পণ ও চাক্রিক প্রতিসমতা প্রদর্শন করে। একটি সুষম অষ্টভুজের শ্লেফলি প্রতীক {8}। সুষম অষ্টভুজের প্রতিটি শীর্ষবিন্দুর অন্তঃকোণ ১৩৫° ($\scriptstyle {\frac {3\pi }{4}}$ রেডিয়ান)। এর বাহুগুলো কেন্দ্রে ৪৫° ($\scriptstyle {\frac {\pi }{4}}$ রেডিয়ান) কোণ উৎপন্ন করে।

ক্ষেত্রফল

a দৈর্ঘ্যের বাহুবিশিষ্ট একটি সুষম অষ্টভুজের ক্ষেত্রফল নির্ণয়ের সূত্র হলো:

$A=2\cot {\frac {\pi }{8}}a^{2}=2(1+{\sqrt {2}})a^{2}\simeq 4.828\,a^{2}.$

অষ্টভুজের পরিবৃত্তের ব্যাসার্ধ R হলে, ক্ষেত্রফল হয়:

$A=4\sin {\frac {\pi }{4}}R^{2}=2{\sqrt {2}}R^{2}\simeq 2.828\,R^{2}.$

অ্যাপথেম r হলে (আরও দেখুন: অন্তর্লিখন) অষ্টভুজের ক্ষেত্রফল হয়:

$A=8\tan {\frac {\pi }{8}}r^{2}=8({\sqrt {2}}-1)r^{2}\simeq 3.314\,r^{2}.$

এর সর্বশেষ দুইটি সহগ একক বৃত্তের ক্ষেত্রফল তথা পাইয়ের মানের মান সংযুক্ত করে।

একটি সুষম অষ্টভুজের ক্ষেত্রফল একটি ভোঁতা-প্রান্তবিশিষ্ট বর্গক্ষেত্রের ক্ষেত্রফলের মাধ্যমে নির্ণয় করা যায়।

সুষম অষ্টভুজের ক্ষেত্রফলকে এভাবেও প্রকাশ করা যায়:

$\,\!A=S^{2}-a^{2},$

যেখানে S হলো অষ্টভুজের বিস্তৃতি বা দ্বিতীয় ক্ষুদ্রতম কর্ণের দৈর্ঘ্য এবং a হলো অষ্টভুজের একটি বাহুর দৈর্ঘ্য। একটি অষ্টভুজের চারপাশের বিপরীত প্রান্তের বাহুগুলোকে বর্ধিত করে একটি বর্গ গঠন করা হলে বর্গের প্রতিটি কোণার ত্রিভুজগুলোকে নিয়ে (৪৫°–৪৫°–৯০° ত্রিভুজ) ত্রিভুজগুলোর সমকোণকে ভেতরে দিয়ে একত্রে নিয়ে বর্গ গঠিত হয়, যা সহজেই প্রমাণ করা যায়। এই বর্গের প্রতিটি বাহুর দৈর্ঘ্য অষ্টভুজের প্রতিটি বাহুর দৈর্ঘ্যের সমান হয়।

একটি বাহুর দৈর্ঘ্য a এবং বিস্তার S হলে

$S={\frac {a}{\sqrt {2}}}+a+{\frac {a}{\sqrt {2}}}=(1+{\sqrt {2}})a\approx 2.414a.$

অর্থাৎ, এর বিস্তৃতি প্রতিটি বাহুর রৌপ্য অনুপাতের সমান। সেক্ষেত্রে অষ্টভুজের ক্ষেত্রফল হয়:

$A=((1+{\sqrt {2}})a)^{2}-a^{2}=2(1+{\sqrt {2}})a^{2}\approx 4.828a^{2}.$

বিস্তারের মাধ্যমে প্রকাশ করা হলে, ক্ষেত্রফল হয়:

$A=2({\sqrt {2}}-1)S^{2}\approx 0.828S^{2}.$

ক্ষেত্রফল নির্ণয়ের আরেকটি সহজ সূত্র হলো:

$\ A=2aS.$

আরও সাধারণভাবে, বর্গাকার বস্তুকে কেটে অষ্টভুজ গঠন করার ক্ষেত্রে বিস্তার S জানা থাকে এবং বাহুর দৈর্ঘ্য a নির্ণয় করতে হয়। সেক্ষেত্রে:

$a\approx S/2.414.$

ভোঁতা-প্রান্তবিশিষ্ট বর্গের কর্তিত বাহুর দৈর্ঘ্য e (চিত্রে সবুজ রঙের ত্রিভুজের বাইরের বাহু) হলে, $e=a/{\sqrt {2}}$ হবে, যার দৈর্ঘ্য নিম্নরূপে নির্ণয় করা যায়:

$\,\!e=(S-a)/2.$

পরিবৃত্ত ও অন্তঃবৃত্তের ব্যাসার্ধ

বাহুর দৈর্ঘ্য a-এর সাপেক্ষে সুষম অষ্টভুজের পরিবৃত্তের ব্যাসার্ধ হবে:

$R=\left({\frac {\sqrt {4+2{\sqrt {2}}}}{2}}\right)a.$

এবং অন্তঃবৃত্তের ব্যাসার্ধ হবে:

$r=\left({\frac {1+{\sqrt {2}}}{2}}\right)a.$

(অর্থাৎ, বাহুর দৈর্ঘ্য a-এর রজত অনুপাতের অর্ধেক গুণ বা মোট বিস্তার S-এর অর্ধেক)

কর্ণ

একটি সুষম অষ্টভুজে তিন ধরনের কর্ণ থাকে:

• ক্ষুদ্র কর্ণ,
• মধ্যম কর্ণ (বিস্তার বা উচ্চতা নামেও পরিচিত), যা অন্তঃবৃত্তের ব্যাসার্ধের দ্বিগুণ, এবং
• দীর্ঘ কর্ণ, যা পরিব্যাসার্ধের দ্বিগুণ।

জ্যামিতিক কর্ণের সাধারণ ধর্ম থেকে এদের দৈর্ঘ্য নির্ণয় করার সূত্রসমূহ হলো:

• ক্ষুদ্র কর্ণ: $a{\sqrt {2+{\sqrt {2}}}}$,
• মধ্যম কর্ণ: $(1+{\sqrt {2}})a$ (রজত অনুপাত-এর a গুণ),
• দীর্ঘ কর্ণ: $a{\sqrt {4+2{\sqrt {2}}}}.$

নির্মাণ

কাগজ ভাঁজ করে সুষম অষ্টভুজ তৈরির প্রণালী

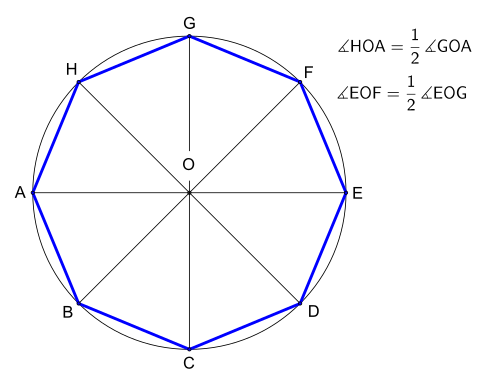
পরিব্যাসার্ধ দেওয়া থাকলে অষ্টভুজ আঁকার পদ্ধতি নিম্নরূপ:

1. একটি বৃত্ত ও এর ব্যাস AOE অঙ্কন করি, যেখানে O পরিবৃত্তের কেন্দ্র এবং A ও E পরিবৃত্তের উপরস্থ দুইটি বিন্দু।
2. AOE ব্যাসের ওপর লম্ব অন্য আরেকটি ব্যাস GOC অঙ্কন করি।
3. A, C, E এবং G একটি বর্গের চারটি শীর্ষবিন্দু নির্দেশ করে।
4. GOA এবং EOG সমকোণদ্বয়ের সমদ্বিখণ্ডক অঙ্কন করি যা পরিবৃত্তের অপর দুইটি ব্যাস HOD এবং FOB নির্দেশ করে।
5. এখন A, B, C, D, E, F, G ও H একটি অষ্টভুজের আটটি শীর্ষবিন্দু নির্দেশ করে।

প্রদত্ত পরিব্যাসার্ধবিশিষ্ট অষ্টভুজ

একটি নির্দিষ্ট দৈর্ঘ্যের বাহুবিশিষ্ট অষ্টভুজ আঁকার অ্যানিমেশনচিত্র। (এই প্রক্রিয়াটি নির্দিষ্ট দৈর্ঘ্যের বাহুবিশিষ্ট ষোড়শভুজ অঙ্কন প্রক্রিয়ার অনুরূপ)

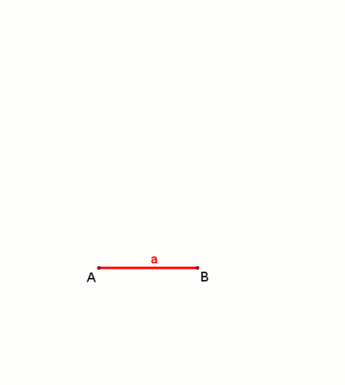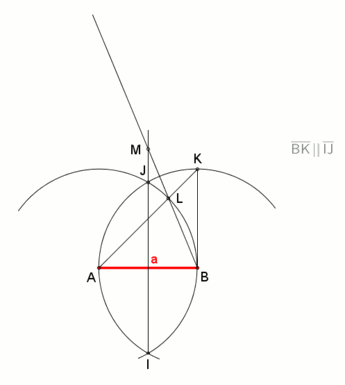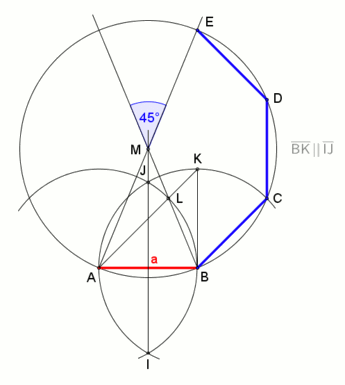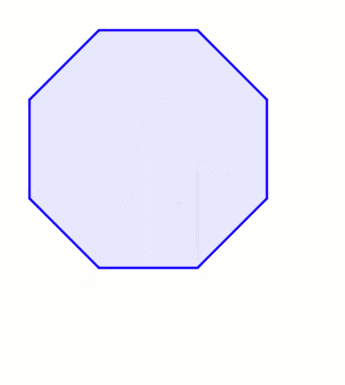
একটি সোজাপ্রান্তবিশিষ্ট মাপদণ্ড ও কম্পাস ব্যবহার করে দুইয়ের ঘাত নিয়মে (৮ = ২^৩) সুষম অষ্টভুজ অঙ্কন করা যায়:

মেকানো অষ্টভুজ

মেকানো দণ্ড ব্যবহার করে সুষম অষ্টভুজ নির্মাণ করা যায়। এজন্য ৪র্থ আকারের বারোটি, ৫ম আকারের তিনটি ও ৬ষ্ঠ আকারের দুইটি দণ্ডের প্রয়োজন।

অষ্টভুজের প্রতিটি বাহু পরিবৃত্তের কেন্দ্রে একটি সমকোণের অর্ধেক পরিমাণ কোণ উৎপন্ন করে। ফলে একটি অষ্টভুজের বাহুর দৈর্ঘ্য a হলে অষ্টভুজের ক্ষেত্রফলকে আটটি সমদ্বিবাহু ত্রিভুজের ক্ষেত্রফলের সমষ্টি হিসেবে নির্ণয় করা যায়। একে নিম্নলিখিতভাবে প্রকাশ করা যায়:

${\text{Area}}=2a^{2}({\sqrt {2}}+1).$

আদর্শ স্থানাঙ্ক

একটি ২ একক দৈর্ঘ্যের সুষম অষ্টভুজের কেন্দ্র মূলবিন্দুতে হলে এর শীর্ষবিন্দুগুলোর স্থানাঙ্ক হবে:

• (±1, ±(1+√২))
• (±(1+√২), ±1).

Dissectibility

8-cube projection	24 rhomb dissection
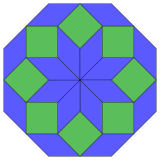	Regular	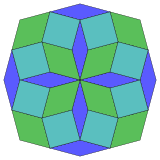Isotoxal

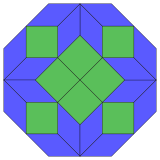
Coxeter states that every zonogon (a 2m-gon whose opposite sides are parallel and of equal length) can be dissected into m(m-1)/2 parallelograms. In particular this is true for regular polygons with evenly many sides, in which case the parallelograms are all rhombi. For the regular octagon, m=4, and it can be divided into 6 rhombs, with one example shown below. This decomposition can be seen as 6 of 24 faces in a Petrie polygon projection plane of the tesseract. The list (ওইআইএস-এ ক্রম A006245) defines the number of solutions as eight, by the eight orientations of this one dissection. These squares and rhombs are used in the Ammann–Beenker tilings.

Regular octagon dissected

Tesseract

4 rhombs and 2 square

Skew

A regular skew octagon seen as edges of a square antiprism, symmetry D_4d, [2⁺,8], (2*4), order 16.

A skew octagon is a skew polygon with eight vertices and edges but not existing on the same plane. The interior of such an octagon is not generally defined. A skew zig-zag octagon has vertices alternating between two parallel planes.

A regular skew octagon is vertex-transitive with equal edge lengths. In three dimensions it is a zig-zag skew octagon and can be seen in the vertices and side edges of a square antiprism with the same D_4d, [2⁺,8] symmetry, order 16.

Petrie polygons

The regular skew octagon is the Petrie polygon for these higher-dimensional regular and uniform polytopes, shown in these skew orthogonal projections of in A₇, B₄, and D₅ Coxeter planes.

A7	D5	B4
7-simplex	5-demicube	16-cell	Tesseract

Symmetry

Symmetry

The eleven symmetries of a regular octagon. Lines of reflections are blue through vertices, purple through edges, and gyration orders are given in the center. Vertices are colored by their symmetry position.

The regular octagon has Dih₈ symmetry, order 16. There are three dihedral subgroups: Dih₄, Dih₂, and Dih₁, and four cyclic subgroups: Z₈, Z₄, Z₂, and Z₁, the last implying no symmetry.

Example octagons by symmetry

r16
d8	g8	p8
d4	g4	p4
d2	g2	p2
a1

On the regular octagon, there are eleven distinct symmetries. John Conway labels full symmetry as r16. The dihedral symmetries are divided depending on whether they pass through vertices (d for diagonal) or edges (p for perpendiculars) Cyclic symmetries in the middle column are labeled as g for their central gyration orders. Full symmetry of the regular form is r16 and no symmetry is labeled a1.

The most common high symmetry octagons are p8, an isogonal octagon constructed by four mirrors can alternate long and short edges, and d8, an isotoxal octagon constructed with equal edge lengths, but vertices alternating two different internal angles. These two forms are duals of each other and have half the symmetry order of the regular octagon.

Each subgroup symmetry allows one or more degrees of freedom for irregular forms. Only the g8 subgroup has no degrees of freedom but can seen as directed edges.

Use

The octagonal floor plan, Dome of the Rock.

The octagonal shape is used as a design element in architecture. The Dome of the Rock has a characteristic octagonal plan. The Tower of the Winds in Athens is another example of an octagonal structure. The octagonal plan has also been in church architecture such as St. George's Cathedral, Addis Ababa, Basilica of San Vitale (in Ravenna, Italia), Castel del Monte (Apulia, Italia), Florence Baptistery, Zum Friedefürsten Church (Germany) and a number of octagonal churches in Norway. The central space in the Aachen Cathedral, the Carolingian Palatine Chapel, has a regular octagonal floorplan. Uses of octagons in churches also include lesser design elements, such as the octagonal apse of Nidaros Cathedral.

Architects such as John Andrews have used octagonal floor layouts in buildings for functionally separating office areas from building services, such as in the Intelsat Headquarters of Washington or Callam Offices in Canberra.

• 
  Umbrellas often have an octagonal outline.
• 
  The famous Bukhara rug design incorporates an octagonal "elephant's foot" motif.
• 
  The street & block layout of Barcelona's Eixample district is based on non-regular octagons
• 
  Janggi uses octagonal pieces.
• 
  Japanese lottery machines often have octagonal shape.
• 
  Stop sign used in English-speaking countries, as well as in most European countries
• 
  An icon of a stop sign with a hand at the middle.
• 
  The trigrams of the Taoist bagua are often arranged octagonally
• 
  Famous octagonal gold cup from the Belitung shipwreck
• 
  Classes at Shimer College are traditionally held around octagonal tables
• 
  The Labyrinth of the Reims Cathedral with a quasi-octagonal shape.
• 
  The movement of the analog stick(s) of the Nintendo 64 controller, the GameCube controller, the Wii Nunchuk and the Classic Controller is restricted by a rotated octagonal area, allowing the stick to move in only eight different directions.

Derived figures

• 
  The truncated square tiling has 2 octagons around every vertex.
  
• 
  An octagonal prism contains two octagonal faces.
  
• 
  An octagonal antiprism contains two octagonal faces.
  
• 
  The truncated cuboctahedron contains 6 octagonal faces.
  
• 
  The omnitruncated cubic honeycomb
  

Related polytopes

The octagon, as a truncated square, is first in a sequence of truncated hypercubes: টেমপ্লেট:Truncated hypercube polytopes As an expanded square, it is also first in a sequence of expanded hypercubes: টেমপ্লেট:Expanded hypercube polytopes

See also

• Bumper pool
• Hansen's small octagon
• Octagon house
• Octagonal number
• Octagram
• Octahedron, 3D shape with eight faces.
• Oktogon, a major intersection in Budapest, Hungary
• Rub el Hizb (also known as Al Quds Star and as Octa Star)
• Smoothed octagon

External links

• Octagon Calculator
• Definition and properties of an octagon With interactive animation