বিপরীত প্রগমন

$a_{n}={\tfrac {1}{n}}$ বিপরীত প্রগমনের প্রথম দশটি পদ।

কোন অনুক্রমের পদগুলোর গুণাত্মক বিপরীত সংখ্যাগুলো যদি একটি সমান্তর প্রগমন গঠন করে তবে এই অনুক্রমটিকে বিপরীত প্রগমন বা বিপরীত অনুক্রম বলা হয়। ভিন্নভাবে বলতে পারি, একটি সমান্তর প্রগমনের পদগুলোর গুণাত্মক বিপরীত সংখ্যাগুলো নিয়ে যে অনুক্রমটি গঠন করা যায় গণিতের ভাষায় সেই অনুক্রমটিই বিপরীত প্রগমন।

একইভাবে বলা যায়, কোন অনুক্রম একটি বিপরীত প্রগমন হবে যদি এর প্রতিটি পদ তার নিকটবর্তী পদগুলোর তথা পূর্ববর্তী ও পরবর্তী পদ দুটির বিপ্রতীপ গড়ের সমান হয়।

অনুরূপভাবে তৃতীয় আরেকটি উপায়ে নিম্নোক্ত আকারের একটি অসীম অনুক্রমের মাধ্যমে বিপরীত প্রগমনের চরিত্র নির্ধারণ করা যায়:

${\frac {1}{a}},\ {\frac {1}{a+d}},\ {\frac {1}{a+2d}},\ {\frac {1}{a+3d}},\cdots ,$

এখানে, a হল একটি অশূন্য সংখ্যা এবং −a/d কোন স্বাভাবিক সংখ্যা নয়।

অথবা নিম্নোক্ত আকারের একটি সসীম অনুক্রমের মাধ্যমেও একে উপস্থাপন করা যায়:

${\frac {1}{a}},\ {\frac {1}{a+d}},\ {\frac {1}{a+2d}},\ {\frac {1}{a+3d}},\cdots ,\ {\frac {1}{a+kd}}$

যেখানে, a হল একটি অশূন্য সংখ্যা, k একটি স্বাভাবিক সংখ্যা এবং −a/d স্বাভাবিক নয় এরূপ একটি সংখ্যা অথবা k এর চেয়ে বড় একটি সংখ্যা।

উদাহরণ

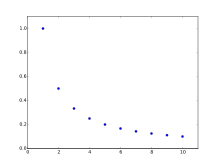
• 1, 1/2, 1/3, 1/4, 1/5, 1/6 হল বিপরীত প্রগমনের একটি সরল উদাহরণ। আরও কয়েকটি নিচে দেওয়া হল:
• 12, 6, 4, 3, ${\tfrac {12}{5}}$, 2, … , ${\tfrac {12}{n}}$, …
• 30, −30, −10, −6, − ${\tfrac {30}{7}}$, … , ${\tfrac {10}{1-{\tfrac {2n}{3}}}}$
• 10, 30, −30, −10, −6, − ${\displaystyle }$, … , ${\tfrac {10}{1-{\tfrac {2(n-1)}{3}}}}$

বিপরীত প্রগমনের সমষ্টি

মূল নিবন্ধ: বিপরীত ধারা

অসীম সংখ্যক পদ নিয়ে গঠিত বিপরীত প্রগমনের সমষ্টি বের করা সম্ভব নয়।

যেসব ভগ্নাংশের লব এক সেগুলোকে একক ভগ্নাংশ বলা হয়। (a = 1 এবং k = 0 এরূপ অতি সামান্য কয়েকটি উদাহরণ ব্যতিত) স্বতন্ত্র একক ভগ্নাংশ নিয়ে গঠিত (অন্যান্য) বিপরীত প্রগমনের সাথে পূর্ণ সংখ্যার সমষ্টি নির্ণয় করা সম্ভব নয়। কারণ হল, প্রগমনের ন্যূনতম একটি হরকে এমন একটি মৌলিক সংখ্যা দ্বারা ভাজ্য হবে যা অন্য কোন হরকে ভাগ করে না।

জ্যামিতিতে প্রয়োগ

A, B, C, এবং D সমরৈখিক বিন্দুগুলো যদি এমন হয় যে, A ও B এর সাপেক্ষে D বিন্দুটি C এর বিপ্রতীপ অনুবন্ধী হয় তাহলে এই চারটি বিন্দুর যেকোন একটি থেকে অপর তিনটির যে দূরত্বগুলো পাওয়া যাবে সেগুলো একটি বিপরীত প্রগমন গঠন করবে। বিশেষকরে AC, AB, AD; BC, BA, BD; CA, CD, CB; এবং DA, DC, DB এই অনুক্রমগুলো বিপরীত প্রগমন হবে, যেখানে প্রতিটি দূরত্ব রেখাটির নির্দিষ্ট দিক বরাবর নির্ধারিত।

কোন ত্রিভুজের উচ্চতাগুলো যদি সমান্তর প্রগমনভুক্ত হয় তবে এর বাহুগুলো বিপরীত প্রগমনভুক্ত হবে।

লিরার হেলানো টাওয়ার

আরও জানতে Block stacking problem ইংরেজি নিবন্ধটি দেখুন।

ব্লক স্ট্যাকিং সমস্যা বা লিরার হেলানো টাওয়ারের উদাহরণ।

বিপরীত প্রগমনের একটি চমৎকার উদাহরণ হল লিরার হেলানো টাওয়ার। এখানে সুষম ব্লক বা পিট্টুগুলোকে একটি আরেকটির উপর এমনভাবে থাক থাক করে রাখা হয় যাতে প্রতিটি ব্লকের কেন্দ্র তার নিচেরটির কেন্দ্র থেকে সর্বাধিক পরিমাণে পার্শ্ব-দূরত্বে থাকে। পিট্টুগুলোকে মূল পিট্টুর (নিচের) 1/2, 1/4, 1/6, 1/8, 1/10, … পার্শ্ব-দূরত্বে এমনভাবে থাক থাক করে রাখা হয় যা মহাকর্ষ বলের কেন্দ্র তথা ভারকেন্দ্রকে ঠিক কাঠামোটির কেন্দ্রে থাকার নিশ্চয়তা দেয় যাতে এটি ধ্বসে না পড়ে। সামান্য একটু ওজন চাপালেই কাঠামোটি অস্থিতিশীল হয়ে পড়ে এবং ভেঙে যায়।

তথ্যসূত্র

• Mastering Technical Mathematics by Stan Gibilisco, Norman H. Crowhurst, (2007) p. 221
• Standard mathematical tables by Chemical Rubber Company (1974) p. 102
• Essentials of algebra for secondary schools by Webster Wells (1897) p. 307