নিট বল
এই নিবন্ধটি অন্য একটি ভাষা থেকে আনাড়িভাবে অনুবাদ করা হয়েছে। এটি কোনও কম্পিউটার কর্তৃক অথবা দ্বিভাষিক দক্ষতাহীন কোনো অনুবাদক কর্তৃক অনূদিত হয়ে থাকতে পারে। |
নিট বল হলো এমন এক ধরনের বলের ভেক্টর যোগফল যা কিনা কোন কণায় বা বস্তুতে ক্রিয়া করে। নিট বল একটি একক বল যা কণার গতিতে মূল বলের প্রভাব কে প্রতিস্থাপন করে। নিউটনের গতির দ্বিতীয় সূত্র অনুসারে এটি কণাকে এই সমস্ত বলের মত একই ত্বরণ দেয়। পদার্থবিদ্যায় কোন নিট বলের প্রয়োগের বিন্দুর সাথে যুক্ত টর্কটি নির্ধারণ করা সম্ভব হয় যাতে এটি বলের মূল সিস্টেমের অধীনে বস্তুর জেট গুলোর চলন বজায় রাখে। এর সাথে সম্পর্কিত টর্ক, নেট শক্তি ফলস্বরূপ শক্তি হয়ে ওঠে এবং বস্তুর আবর্তিত গতিতে একই প্রভাব ফেলে। [১]
সর্বমোট শক্তি[সম্পাদনা]

বল একটি ভেক্টর পরিমাণ যার অর্থ এটির একটি মান রয়েছে এবং দিক রয়েছে এবং এটি সাধারণত বোল্ডফেস ব্যবহার করে যেমন এফ হিসাবে বা উপরে তীর চিহ্নের মতো ব্যবহার করে। উদাহরণস্বরূপ //ডিসপ্লে ধরন এবং /স্ক্রিপ্ট ধরন। খন্ডের এ বি এর দৈর্ঘ্য বলের দৈর্ঘ্যের প্রতিনিধিত্ব করে। ভেক্টর ক্যালকুলাস ১৮০০ দশকের শেষের দিকে এবং ১৯০০ দশকের গোড়ার দিকে বিকশিত হয়েছিল। বল সমূহ সংযোজনের জন্য ব্যবহৃত সমান্তরাল বিধিটি প্রাচীনকাল থেকে এসেছে। গ্যালিলিও এবং নিউটন স্পষ্টভাবে তা বিশ্লেষণ করেছেন। [২] বর্ধিত অংশে প্রয়োগ করা বলের বিভিন্ন প্রয়োগবিন্দু থাকতে পারে। বল সীমাবদ্ধ ভেক্টর এবং তারা একই বিন্দুতে প্রয়োগ করা হয় তবেই যুক্ত করা যায়।
বলসমূহ যোগ করার জন্য সমান্তরাল বিধি[সম্পাদনা]

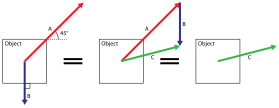
একটি বল একটি বাউন্ড ভেক্টর নামে পরিচিত-যার অর্থ এটি একটি দিক, প্রস্থ এবং একটি প্রয়োগ বিন্দু রয়েছে। একটি বলকে সহজভাবে সংজ্ঞায়িত করার জন্য একটি বিন্দু থেকে আরেকটি বিন্দুতে সংযোগ সংযোগ স্থাপন করা। A বিন্দু থেকে B বিন্দু পর্যন্ত। যদি আমরা এই পয়েন্টগুলির স্থানাঙ্কগুলি A = (Ax, Ay, Az) এবং B = (Bx, By, Bz) হিসাবে চিহ্নিত করি তবে A এ প্রয়োগ করা বল ভেক্টর দ্বারা প্রদত্ত
ভেক্টরের দৈর্ঘ্য B-A এবং এর বিশালতা ব্যাখ্যা করে F এবং এর দ্বারা বুঝা যায়
দুটি বলের গণিত F1 এবং F2 এ প্রয়োগ হয় A অংশ গণিত বিশ্লেষণ করলে দেখা যায় F1=B-A এবং F2=D-A, এরপর দুটি ভেক্টরের গাণিতিক
যা এভাবে লেখা যায়
যেখানে E চিহ্নিত করা আছে BD এটা মিলন স্থলে মিলিত হয়B এবং D. সুতরাং বলগুলোর F1 এবং F2 এর যোগফল টি দুটি বলের শেষ বিন্দু B এবং D তে যোগ করলে দেখা যায় এর মধ্যবিন্দুর মান মধ্যভাগের দ্বিগুণ। সমান্তরাল ABDC সংজ্ঞায়িত করতে যথাক্রমে AB এবং AD এর সমান্তরাল BC এবং DC বিভাগ গুলো কে সংজ্ঞায়িত করে এই দৈর্ঘ্যের দ্বিগুণ দৈর্ঘ্য সহজেই অর্জন করা যায়।
একটি বলের কারণে স্থানান্তর এবং ঘূর্ণন[সম্পাদনা]
যখন একটি শক্তি একটি একক বিন্দুর উপর কাজ করে তখন এটি একটি একক বিন্দুতে প্রয়োগ করা হয়(কণার পরিমাণটি নগণ্য নয়): এটি একটি বিন্দু শক্তি এবং কণা এটির প্রয়োগ বিন্দু। তবে একটি বর্ধিত শরীরে (বস্তু) একটি বাহ্যিক শক্তি তার অঞ্চলের কণাগুলির বেশ কয়েকটি তে প্রয়োগ করা যেতে পারে অর্থাৎ শরীরের উপর কিছু পরিমাণে বা পৃষ্ঠের উপর ছড়িয়ে যেতে পারে। তবে শরীরের উপর এর ঘূর্ণন প্রভাব নির্ধারণের জন্য আমরা এর প্রয়োগের বিন্দুটি নির্বাচন করতে চাই(আসলে প্রয়োগের রেখাটি নিচে বর্ণিত হিসাবে): সমস্যাটি সাধারণত নিম্নলিখিত উপায়ে সমাধান করা যায়
•প্রায়শই ভলিয়ম বা পৃষ্ঠ যার উপর বলপ্রয়োগ কাজ করে তা শরীরের আকারের তুলনায় তুলনামূলকভাবে ছোট হয় যাতে এটি একটি বিন্দু দারা সীমাবদ্ধ হতে পারে। এই ধরনের আনুমানিক বিষয়ের কারণে ত্রুটি গ্রহণযোগ্য কিনা তা নির্ধারণ করা সাধারণত কঠিন কাজ নয়।
•যদি একটি গ্রহণযোগ্য না হয় (স্পষ্ট উদাহরণস্বরূপ মহাকর্ষ বলের ক্ষেত্রে)। এজাতীয় ভলিউম বা পৃষ্ঠ বলটিকে সিস্টেম এর উপাদান হিসেবে বর্ণনা করা উচিত, প্রতিটি একক কণায় অভিনয় করে এবং তার জন্য গণনা করা উচিত তাদেরকে পৃথকভাবে। এই জাতীয়় গণনা সাধারনত পদার্থের পরিমাণ বা পৃষ্ঠের ডিফারেন্সিয়াল উপাদান এবংং অবিচ্ছেদ্য ক্যালকুলাস ব্যবহার করে সহজ হয়। বেশ কয়েকটি ক্ষেত্রে যদিও দেখা যায় যে এ জাতীয় বলের একটিি সিস্টেমের আসল গণনা ছাড়াই একক বিন্দু শক্তি দ্বারা প্রতিস্থাপন করা যেতে পারে। যাই হোক না কেন অনমনীয় বস্তুর গতির বিশ্লেষণ বিন্দু বলের মডেল দিয়ে শুরু হয়।
অনমনীয় বস্তু[সম্পাদনা]

চিত্রের বিপরীতে চিত্রিত স্থানে দেখানো হয়েছে যে একটি একক শক্তি কীভাবে একটি নিখড় অনর বস্তুর প্রয়োগ বিন্দুতে কাজ করে। শরীরে ভর M এবং এর ভর কেন্দ্র বিন্দু C হয় ধ্রুবক ভর আনুমানিকভাবে, বল নিম্নোক্ত অভিব্যক্তি দ্বারা বর্ণিত বস্তুর গতিতে পরিবর্তন ঘটায়:
- এটা হলো গতির প্রাণ বিন্দু; এবং
- এটা হলো বস্তুর কৌণিক গতি।
দ্বিতীয় ক্ষেত্রে, এটা হলো টর্ক অথবা বলের গতি বেগ, whereas এটা হলো বস্তুর জড়তার ভরবেগ । একটি বলের দ্বারা টর্ক তৈরি হয় নিম্নোক্ত কিছু বিন্দু দারা ব্যাখ্যা করা হলো:
- এটা হলো টর্ক ভেক্টর, এবং
- এটা হলো ভেক্টরের পরিমাণ.
এই ভেক্টর টি বল প্রয়োগ বিন্দুর অবস্থান ভেক্টর এবং এই উদাহরণে এটি ভরকেন্দ্রের থেকে রেফারেন্স বিন্দু হিসেবে আঁকা হয়। চিত্রটি অনুযায়ী টর্কের পরিবর্তন হবে না (একই লিভার আর্ম), যদি প্রয়োগের বিন্দু বলের বিন্দুর সাথে অথবা বল প্রয়োগের বিন্দুর সাথে সরানো হয়। আরো আনুষ্ঠানিকভাবে এই ভেক্টর কণাগুলোর বৈশিষ্ট্য থেকে অনুসরণ করে এবং দেখায় যে বলগুলোর ঘূর্ণন প্রভাব কেবল তার প্রয়োগের রেখার অবস্থানের উপর নির্ভর করে। টর্ক ভেক্টরটি বল এবং ভেক্টর দারা সংজ্ঞায়িত কোন সমতলের জন্য লম্ব হয় এবং এই উদাহরণে এটি পর্যবেক্ষকের দিকে পরিচালিত হয় যে; কৌণিক ত্বরণ ভেক্টরের একই দিক রয়েছে। ডান হাতের নিয়মটি ঘড়ির কাটার দিকে অথবা ঘড়ির কাঁটার বিপরীতে ঘুরার সাথে সম্পর্কিত করে।
ফলস্বরূপ বল[সম্পাদনা]
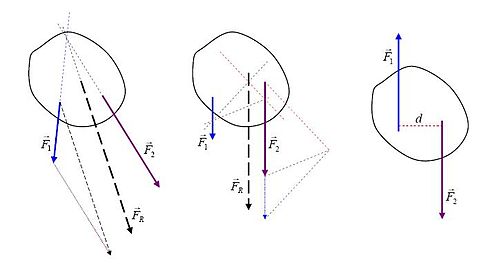
ফলস্বরূপ বল এবং টর্ক একটি দৃঢ় শরীরের চলাফেরায় অভিনয় করে এমন একটি বাহিনীর সিস্টেমের প্রভাবগুলিকে প্রতিস্থাপন করে। একটি আকর্ষণীয় বিশেষ কেসটি একটি টর্ক-মুক্ত ফলাফল, যা নিম্নলিখিত হিসাবে পাওয়া যেতে পারে
১•নিট বল খুঁজে পেতে ভেক্টর সংযোজন ব্যবহৃত হয়। ২•0 টর্ক দিয়ে প্রয়োগের বিন্দু নির্ধারণ করতে এই সমীকরণ টি ব্যবহার করুন:
যেখানে হল নিট বল, এটা এর অ্যাপ্লিকেশন বিন্দুতে অবস্থান করে, এবং আলাদা আলাদা বলগুলো হল অ্যাপ্লিকেশন বিন্দুর সাথে . এটা হতে পারে যে সেখানে কোন অ্যাপ্লিকেশন বিন্দু নেই যা কিনা মুক্ত টর্ক উৎপন্ন করবে।
১• উপরের সমীকরণটির কোন সমাধান হতে পারে। সেক্ষেত্রে কোন ফল স্বরূপ শক্তি নেই অর্থাৎ কোনও একক শক্তিই দেহের রৈখিক এবং কৌণিক ত্বরণ উভয় সম্পর্কিত সমস্ত প্রকৃত বাহিনীকে প্রতিস্থাপন করতে পারে না। এবং যখন গণনা করা যায় তখনও এটি অনন্য নয়, কারণ অ্যাপ্লিকেশন পয়েন্টটি টর্কে প্রভাবিত না করেই অ্যাপ্লিকেশনটির লাইন ধরে এগিয়ে যেতে পারে।
২• চিত্রের মধ্যবর্তী চিত্রটি দুটি সমান্তরাল প্রকৃত বল দেখায়। ভেক্টর সংযোজনের পরে "নিট বলের অবস্থানটিকে প্রয়োগের বিন্দুতে যথার্থ অনুবাদ করা হয় যেখানে এটি ফলাফল শক্তি হয়ে যায়। প্রক্রিয়াটি সমস্ত শক্তিকে এমন উপাদানে বিভক্ত করার উপর ভিত্তি করে তৈরি করা হয় যার জন্য আবেদনের রেখাগুলো ছেদ করে একপর্যায়ে (মেরুটি চিত্রের ডানদিকে সংযোজন করা হয়)।
৩• ডান দিকের চিত্রর টি একটি জোড়া দেখায়। দুটোই সমান কিন্তু বিপরীত বল যার জন্য নিট বলের পরিমাণ শূন্য। তবে তারা নিট তর্ টর্ককে উৎপাদন করে তাদের প্রয়োগের লাইনের মধ্যবর্তী দূরত্বে রাখে।
ব্যবহার[সম্পাদনা]
সাধারণভাবে, শক্ত কাঠামোয় শৃংখলা রক্ষাকারি বল গুলো সর্বদা একটি বল এবং টর্ক দ্বারা প্রতিস্থাপিত হতে পারে। বলটি নিট শক্তি। তবে অতিরিক্ত টর্ক গণনা করতে নিট বলের কর্মের রেখাটি অবশ্যই নির্ধারণ করতে হবে। ক্রিয়াটির রেখাটি নির্বিচারে নির্বাচন করা যেতে পারে তবে অতিরিক্ত নিট বা খাঁটি টর্কটি এই বিষয়ের উপর নির্ভর করে। একটি বিশেষ ক্ষেত্রে এমন টর্কের শূন্য ক্রিয়া-কলাপ এর এমন রেখা পাওয়া সম্ভব।
কিছু লেখক পরিসমাপ্তি বলটিকে নেট বল থেকে পৃথক করেন না এবং শব্দের প্রতিশব্দ হিসাবে ব্যবহার করেন। [৩]
আরও দেখুন[সম্পাদনা]
তথ্যসূত্র[সম্পাদনা]
- ↑ Symon, Keith R. (1964), Mechanics, Addison-Wesley, এলসিসিএন ৬০-৫১৬৪
- ↑ Michael J. Crowe (1967). A History of Vector Analysis : The Evolution of the Idea of a Vectorial System. Dover Publications (reprint edition; আইএসবিএন ০-৪৮৬-৬৭৯১০-১).
- ↑ Resnick, Robert and Halliday, David (1966), Physics, (Vol I and II, Combined edition), Wiley International Edition, Library of Congress Catalog Card No. 66-11527
















