নববিন্দু বৃত্ত

কোন ত্রিভুজের তিনটি বাহুর মধ্যবিন্দুত্রয়, শীর্ষবিন্দুগুলো থেকে বিপরীত বাহুর উপর অঙ্কিত লম্ব তিনটির পাদবিন্দুত্রয় এবং ত্রিভুজটির লম্বকেন্দ্র থেকে এর প্রতিটি শীর্ষের মধ্যবর্তী রেখাংশের মধ্যবিন্দুত্রয় মোট এই নয়টি বিশেষ সমবৃত্তীয় বিন্দু দিয়ে যে বৃত্তটি অতিক্রম করে তাকে জ্যামিতির ভাষায় নববিন্দু বৃত্ত বলা হয়।^[১]^[২] আর নববিন্দু বৃত্তের কেন্দ্রকে বলা হয় নববিন্দু কেন্দ্র যা আবার ঐ ত্রিভুজটির একটি ত্রিভুজ কেন্দ্র। নববিন্দু বৃত্ত এমনই একটি বৃত্ত যা সকল ত্রিভুজের ক্ষেত্রেই পাওয়া যাবে। উপর্যুক্ত নয়টি বিশেষ বিন্দু দিয়ে গঠিত হওয়ায় কাঠামোটির এরূপ নাম।

এছাড়াও নববিন্দু বৃত্ত আরও কয়েকটি নামে পরিচিত। যথা: ফয়েরবাখের বৃত্ত, অয়লারের বৃত্ত, টারকেমের বৃত্ত, ষড়বিন্দু বৃত্ত, দ্বাদশবিন্দু বৃত্ত, n-বিন্দু বৃত্ত, মধ্যঅন্তর্লিখিত বৃত্ত (medioscribed), মধ্য বৃত্ত (mid circle) অথবা পরিমধ্যবৃত্ত (circum-midcircle)।^[৩]^[৪]

গুরুত্বপূর্ণ নয়টি বিন্দু[সম্পাদনা]

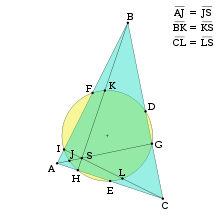
উপরের চিত্রে নববিন্দু বৃত্তের গুরুত্বপূর্ণ নয়টি বিন্দু দেখানো হয়েছে। D, E এবং F হলো ত্রিভুজের বাহু তিনটির মধ্যবিন্দু। G, H এবং I হলো ত্রিভুজটির তিনটি শীর্ষবিন্দু (A, B, এবং C) থেকে বিপরীত বাহুগুলোর উপর অঙ্কিত লম্বগুলোর পাদবিন্দু। J, K এবং L হলো ত্রিভুজটির প্রতিটি শীর্ষবিন্দু আর লম্বকেন্দ্র S এর সংযোজক রেখাংশগুলোর মধ্যবিন্দু।

সূক্ষ্মকোণী ত্রিভুজের ক্ষেত্রে লম্বকেন্দ্র থেকে এর প্রতিটি শীর্ষের মধ্যবর্তী রেখাংশের মধ্যবিন্দুত্রয় এবং শীর্ষগুলো থেকে বিপরীত বাহুর উপর অঙ্কিত লম্ব তিনটির পাদবিন্দুত্রয় মোট এই ছয়টি বিন্দু ঐ ত্রিভুজটির উপরই অবস্থান করবে। স্থূলকোণী ত্রিভুজের ক্ষেত্রে উক্ত পাদ বিন্দু তিনটির মধ্যে দুটি বিন্দু ত্রিভুজটির বাইরে অবস্থান করবে, তথাপি সেগুলো নববিন্দু বৃত্তের অন্তর্ভুক্ত বলে গণ্য হবে।

আবিষ্কার[সম্পাদনা]

নববিন্দু বৃত্ত আবিষ্কারের কৃতিত্ব কার্ল উইলহেম ফয়েরবাখকে দেওয়া হলেও তিনি পূর্ণাঙ্গভাবে এর আবিষ্কার করেননি। তিনটি বাহুর মধ্যবিন্দু ও এবং তিনটি বিপরীত বাহুর উপর টানা লম্বের তিনটি পাদবিন্দু মোট এই ছয়টি বিন্দু যে ষড়বিন্দু বৃত্তের জন্য তাৎপর্যপূর্ণ বলে স্বীকৃত তিনি বরং সেটি আবিষ্কার করেন। (চিত্র ৩ এর D, E, F, G, H এবং I বিন্দুগুলো লক্ষ্য করুন)। এর কিছুদিন পূর্বেই চার্লস জুলিয়েন ব্রায়ানশন এবং জ্যাঁ-ভিক্টর পৌন্সলে একই উপপাদ্যের বর্ণনা এবং প্রমাণ দেন। কিন্তু ফয়েরবাখের অল্প কিছু দিন পরেই গণিতবিদ অলরি টারকেম এককভাবে বৃত্তটির অস্তিত্বের প্রমাণ করেন। ত্রিভুজের শীর্ষবিন্দু ও লম্বকেন্দ্রের মধ্যবর্তী রেখাংশের মধ্যবিন্দু তিনটির বাড়তি তাৎপর্য তিনিই সর্বপ্রথম বুঝতে পারেন। (চিত্র ৩ এর J, K এবং L বিন্দুগুলো দেখুন)। এই কারণে টারকেম হলেন নববিন্দু বৃত্ত নামটি ব্যবহারকারী প্রথম ব্যক্তি।

স্পর্শকীয় বৃত্ত[সম্পাদনা]

একটি ত্রিভুজের নববিন্দু বৃত্ত ত্রিভুজটির অন্তর্বৃত্ত ও বহির্বৃত্তগুলোর স্পর্শক হবে।

১৮২২ সালে কার্ল ফয়েরবাখ প্রমাণ করেন যে, যেকোন ত্রিভুজের নববিন্দু বৃত্তটি ত্রিভুজটির তিনটি বহির্বৃত্তকে বাইরে থেকে স্পর্শ করবে এবং ত্রিভুজের অন্তর্বৃত্তটিকে ভিতরের দিক থেকে স্পর্শ করবে। এই ফলাফলটি ফয়েরবাখের উপপাদ্য নামে পরিচিত। তিনি প্রমাণ করেন যে:

...ত্রিভুজের শীর্ষত্রয় থেকে বিপরীত বাহুর উপর অঙ্কিত লম্ব তিনটির পাদবিন্দুত্রয় দিয়ে অতিক্রমকারী বৃত্তটি, ঐ ত্রিভুজের বাহুত্রয়ের স্পর্শক এমন চারটি বৃত্তের প্রতিটির স্পর্শক হবে... (ফয়েরবাখ, ১৮২২)

অন্তর্বৃত্ত এবং নববিন্দু বৃত্ত যে ত্রিভুজ কেন্দ্রে পরস্পরকে স্পর্শ করে তাকে ফয়েরবখ বিন্দু বলা হয়।

নববিন্দু বৃত্তের অন্যান্য ধর্ম[সম্পাদনা]

একটি ত্রিভুজের পরিবৃত্তের ব্যাসার্ধ ত্রিভুজটির নববিন্দু বৃত্তের ব্যাসার্ধের দ্বিগুণ।^[৫]^:p.১৫৩

চিত্র ৪

একটি ত্রিভুজের লম্বকেন্দ্র থেকে ত্রিভুজটির পরিবৃত্তের যেকোন বিন্দুর মধ্যবর্তী সংযোজক রেখাংশ ত্রিভুজটির নববিন্দু বৃত্তের দ্বারা সমদ্বিখণ্ডিত হবে।

চিত্র ৫

একটি ত্রিভুজের লম্বকেন্দ্র H এবং পরিকেন্দ্র (পরিবৃত্তের কেন্দ্র) O এর সংযোজক রেখাংশটি ত্রিভুজটির নববিন্দু বৃত্তের কেন্দ্র N দ্বারা সমদ্বিখণ্ডিত হবে। উপরন্তু এই লম্বকেন্দ্রটি নববিন্দু বৃত্ত ও পরিবৃত্ত উভয়েরই সম্প্রসারণের একটি কেন্দ্র হবে:^[৫]^:p.১৫২

ON = NH

কোন ত্রিভুজের নববিন্দু কেন্দ্র N ত্রিভুজটির অয়লার রেখা বরাবর ত্রিভুজটির ভরকেন্দ্র G থেকে লম্বকেন্দ্র H এর দিকে এক-চতুর্থাংশ দূরত্বে অবস্থান করে:^[৫]^:p.১৫৩

HN = 3NG

দ্বিমধ্যমা (bimedian) হলো চতুর্ভুজের বিপরীত দুটি বাহুর মধ্যবিন্দুর সংযোজক রেখাংশ। একটি বৃত্তীয় চতুর্ভুজের কর্ণীয় ত্রিভুজের $\omega$ নববিন্দু বৃত্তটি বিবেচনা করা যাক। বৃত্তীয় চতুর্ভুজটির দ্বিমধ্যমা দুটির ছেদবিন্দুটি এই নববিন্দু বৃত্তটির অন্তর্ভুক্ত হবে।^[৬]^[৭]

কোন ত্রিভুজের নববিন্দু বৃত্তটি ঐ ত্রিভুজটির মধ্যবিন্দু ত্রিভুজের পরিবৃত্ত হবে কারণ মধ্যবিন্দু ত্রিভুজের শীর্ষবিন্দুগুলো মূল ত্রিভুজটির বাহুগুলোর মধ্যবিন্দু। আবার ত্রিভুজের নববিন্দু বৃত্তটি ঐ ত্রিভুজটির লম্বিক ত্রিভুজেরও পরিবৃত্ত হবে কারণ লম্বিক ত্রিভুজের শীর্ষবিন্দুগুলো এক্ষেত্রে মূল ত্রিভুজটির উচ্চতা রেখাগুলোর পাদবিন্দু হবে।^[৫]^:p.১৫৩
একটি ত্রিভুজের শীর্ষবিন্দুগুলো দিয়ে অতিক্রমকারী সকল আয়তাকার অধিবৃত্তের কেন্দ্র ঐ ত্রিভুজটির নববিন্দু বৃত্তের উপর অবস্থান করবে। এর উদাহরণ হিসেবে কিপার্ট, এশাবেক এবং ফয়েরবাখের আয়তক্ষেত্রের উল্লেখ করা যায়। এই বিষয়টি ফয়েরবাখের কনিক উপপাদ্য নামে পরিচিত।

যদি A, B, C এবং H বিন্দু চারটি নিয়ে গঠিত কোন লম্বকেন্দ্রিক ব্যবস্থায় তিনটি নির্দিষ্ট বিন্দুর যেকোন প্রকার সমাবেশে চারটি ত্রিভুজ গঠন করা হয় তবে এদের সকলের একই নববিন্দু বৃত্ত পাওয়া যাবে যা প্রতিসাম্যের একটি ধারাবাহিকতা। একটি ত্রিভুজের কোন শীর্ষবিন্দু অপর আরেকটি ত্রিভুজের লম্বকেন্দ্র হলে এই শীর্ষবিন্দুর সন্নিহিত বাহুদুটি দ্বিতীয় ত্রিভুজটিরই রেখাংশ হবে। তৃতীয় একটি মধ্যবিন্দু উভয়ের সাধারণ বাহুর উপর অবস্থান করবে। এই একই মধ্যবিন্দুগুলো পৃথক পৃথক নববিন্দু বৃত্তকে নির্দেশ করে এবং এই বৃত্তগুলো অবশ্যই পরস্পরের উপর সমাপতিত (concurrent) হবে।

ফলস্বরূপ, এই চারটি ত্রিভুজের অভিন্ন ব্যাসার্ধ যুক্ত পরিবৃত্ত রয়েছে। সাধারণ নববিন্দু কেন্দ্রকে N দ্বারা উপস্থাপন করা যাক। ধরাযাক, লম্বকেন্দ্রিক সিস্টেমটির সমতলে P স্বাধীন বা ইচ্ছামতো একটি বিন্দু। তাহলে আমরা পাব—

NA²+NB²+NC²+NH² = 3R²

এখানে R হলো সাধারণ পরিব্যাসার্ধ (পরিবৃত্তের ব্যাসার্ধ)।

আরও ধরাযাক, K একটি ধ্রুবক। এখন যদি

PA²+PB²+PC²+PH² = K² হয়,

তাহলে P বিন্দুটির লোকাস একটি বৃত্ত হবে যা N বিন্দুতে কেন্দ্রিভূত হবে এবং এর ব্যাসার্ধ হবে

\scriptstyle {\frac {1}{2}}{\sqrt {K^{2}-3R^{2}}}

। যখন P বিন্দুটি নববিন্দু কেন্দ্র N এ পৌঁছে তখন ধ্রুবক K অনুসারে P এর লোকাসটি N বিন্দুতে পতিত হয়। উপরন্তু নববিন্দু বৃত্তটিও P এর লোকাস যেখানে,

PA²+PB²+PC²+PH² = 4R².

ত্রিভুজের অন্তর্বৃত্ত ও বহির্বৃত্তের কেন্দ্রগুলো একটি লম্বকেন্দ্রিক ব্যবস্থা গঠন করে। এই লম্বকেন্দ্রিক ব্যবস্থার জন্য গঠিত নববিন্দু বৃত্তটি মূল ত্রিভুজটির পরিবৃত্ত হবে। লম্বকেন্দ্রিক ব্যবস্থায় উচ্চতারেখাগুলোর পাদবিন্দুগুলো মূল ত্রিভুজটির শীর্ষবিন্দু।

A, B, C এবং D ঐচ্ছিক বিন্দু চারটি কোন লম্বকেন্দ্রিক ব্যবস্থা গঠন না করে তাহলে ABC, BCD, CDA এবং DAB ত্রিভুজের নববিন্দু বৃত্তগুলো কোন একটি বিন্দুতে সমবিন্দুগামী হবে। এই নববিন্দু বৃত্তগুলোর অবশিষ্ট ছয়টি ছেদবিন্দুর প্রতিটি উক্ত চারটি ত্রিভুজের মধ্যবিন্দুগুলোতে সমাপতিত হবে। বিশেষভাবে উল্লেখ করার মতো বিষয় এই যে, এই চারটি ঐচ্ছিক বিন্দুর ভরকেন্দ্রে কেন্দ্রিভূত হয় এমন একটি স্বতন্ত্র নববিন্দু কনিকের অস্তিত্ব রয়েছে যা এই নববিন্দু বৃত্তগুলোর সাতটি ছেদবিন্দুর প্রতিটির মধ্য দিয়ে অতিক্রম করে। অধিকন্তু, উপরে উল্লেখিত ফয়েরবাখের কনিক উপপাদ্যের কারণে এমন একটি আয়তাকার স্বতন্ত্র সার্কামকনিকের অস্তিত্ব রয়েছে যার কেন্দ্র চারটি নববিন্দু বৃত্তের সাধারণ ছেদবিন্দুতে অবস্থিত এবং এই সার্কামকনিকটি মূল চারটি ঐচ্ছিক বিন্দু দিয়ে অতিক্রম করার পাশাপাশি ঐ চারটি ত্রিভুজের লম্বকেন্দ্রগুলো দিয়েও অতিক্রম করে।

যদি A, B, C এবং D বিন্দু চারটি একটি বৃত্তীয় চতুর্ভুজ গঠন করে তাহলে ABC, BCD, CDA এবং DAB ত্রিভুজের নববিন্দু বৃত্তগুলোর প্রতিটিই বৃত্তীয় চতুর্ভুজটির প্রতিকেন্দ্র (anticenter) দিয়ে গমন করবে (concur) অর্থাৎ এরা প্রতিকেন্দ্রে সমবিন্দুগামী হবে। নববিন্দু বৃত্তগুলোর প্রতিটি বৃত্তীয় চতুর্ভুজটির পরিবৃত্তের ব্যাসার্ধের অর্ধেকের সমান ব্যাসার্ধের একটি বৃত্তের সর্বসম হবে। নববিন্দু বৃত্তগুলো চারটি জনসন বৃত্তের একটি সেট গঠন করে। ফলস্বরূপ, এই চারটি নববিন্দু কেন্দ্র বৃত্তীয় হবে এবং এই চারটি নববিন্দু বৃত্তের সর্বসম একটি বৃত্তের উপর অবস্থান করবে যেখানে এই সর্বসম বৃত্তটির কেন্দ্র বৃত্তীয় চতুর্ভুজটির প্রতিকেন্দ্রে (anticenter) অবস্থান করবে। উপরন্তু এই চারটি নববিন্দু কেন্দ্র দিয়ে গঠিত বৃত্তীয় চতুর্ভুজটি −¹/₂ গুণকটির মাধ্যমে মূল (প্রসঙ্গ) বৃত্তীয় চতুর্ভুজ ABCD এর হোমোথেটিক হবে এবং এর হোমোথেটিক কেন্দ্র N, পরিকেন্দ্র O এবং প্রতিকেন্দ্র M এর সংযোজক রেখার উপর অবস্থান করবে যেখানে

ON = 2NM

পরিকেন্দ্র দিয়ে গমনকারী রেখাগুলোর লম্বমেরুটি (orthopole) নববিন্দু বৃত্তে অবস্থান করে।
একটি ত্রিভুজের পরিবৃত্ত, নববিন্দু বৃত্ত, মেরুবৃত্ত এবং এই ত্রিভুজের স্পর্শকীয় ত্রিভুজের পরিবৃত্ত^[৮] সম অক্ষীয় হবে।^[৯]
কিপার্ট অধিবৃত্তের ত্রিরৈখিক স্থানাঙ্কগুলো হবে:

(b² − c²)²/a : (c² − a²)²/b : (a² − b²)²/c

এশাবেক অধিবৃত্তের জন্য ত্রিরৈখিক স্থানাঙ্কগুলো হবে:

cos A sin²(B − C) : cos B sin²(C − A) : cos C sin²(A − B)

ত্রিরৈখিক স্থানাঙ্কব্যবস্থায় x : y : z কোন পরিবর্তনশীল বিন্দু হলে নিচের সমীকরণটি নববিন্দু বৃত্তের একটি সমীকরণ হবে:

x²sin 2A + y²sin 2B + z²sin 2C − 2(yz sin A + zx sin B + xy sin C) = 0

সাধারণিকরণ[সম্পাদনা]

বৃত্ত হলো কনিকের একটি উদাহরণ। অনুরূপভাবে নববিন্দু বৃত্ত হলো সাধারণ নব বিন্দু কনিকের এমন একটি উদাহরণ যা একটি ত্রিভুজ এবং একটি চতুর্থ বিন্দুর (ABC ত্রিভুজ এবং P বিন্দু) সাপেক্ষে গঠিত যেখানে P বিন্দুটি ABC এর লম্বকেন্দ্র হলে নববিন্দু বৃত্ত নামের এই নির্দিষ্ট বৃত্তের প্রসঙ্গটি চলে আসে। ত্রিভুজের শীর্ষবিন্দুগুলো এবং P বিন্দুটি একটি পূর্ণ চতুর্ভুজকে এবং চতুর্ভুজের বিপরীত বাহুগুলো পরস্পরকে ছেদ করে এরূপ তিনটি "কর্ণবিন্দু" নির্দেশ করে। একটি চতুর্ভুজের ছয়টি "পার্শ্ববাহু" (sideline) থাকে; নববিন্দু কনিক এদের মধ্যবিন্দুগুলোকে ছেদ করে এবং কর্ণবিন্দুগুলোও এদের অন্তর্ভুক্ত। যখন P বিন্দুটি ABC ত্রিভুজের ভিতরে থাকে অথবা ত্রিভুজটির সাথে বিপ্রতীপ কোণসমূহ গঠন করে এমন একটি অঞ্চলে থাকে তখন কনিকটি একটি উপবৃত্ত হয়। কিন্তু তিনটি সন্নিহিত অঞ্চলের একটিতে P বিন্দুটি থাকলে কনিকটি একটি নববিন্দু অধিবৃত্ত হয়, আর P বিন্দুটি ABC ত্রিভুজের পরিবৃত্তের উপরে অবস্থান করলে অধিবৃত্তটি আয়তক্ষেত্রে রূপান্তরিত হয়।

তথ্যসূত্র[সম্পাদনা]

↑ Altshiller-Court (1925, pp. 103–110)
↑ Kay (1969, pp. 18,245)
↑ Kocik, Jerzy; Solecki, Andrzej (২০০৯)। "Disentangling a Triangle"। Amer. Math. Monthly। 116 (3): 228–237। ডিওআই:10.4169/193009709x470065। Kocik and Solecki (sharers of a 2010 Lester R. Ford Award) give a proof of the Nine-Point Circle Theorem.
↑ Casey, John (১৮৮৬)। Nine-Point Circle Theorem, in A Sequel to the First Six Books of Euclid (4th সংস্করণ)। London: Longmans, Green, & Co। পৃষ্ঠা 58।
↑ ^ক ^খ ^গ ^ঘ Posamentier, Alfred S., and Lehmann, Ingmar. The Secrets of Triangles, Prometheus Books, 2012.
↑ Fraivert, David (জুলাই ২০১৯)। "New points that belong to the nine-point circle"। The Mathematical Gazette। 103 (557): 222–232। ডিওআই:10.1017/mag.2019.53।
↑ Fraivert, David (২০১৮)। "New applications of method of complex numbers in the geometry of cyclic quadrilaterals" (পিডিএফ)। International Journal of Geometry। 7 (1): 5–16।
↑ Altshiller-Court (1925, p. 98)
↑ Altshiller-Court (1925, p. 241)

[1] Altshiller-Court (1925, pp. 103–110)

[2] Kay (1969, pp. 18,245)

[3] Kocik, Jerzy; Solecki, Andrzej (২০০৯)। "Disentangling a Triangle"। Amer. Math. Monthly। 116 (3): 228–237। ডিওআই:10.4169/193009709x470065। Kocik and Solecki (sharers of a 2010 Lester R. Ford Award) give a proof of the Nine-Point Circle Theorem.

[4] Casey, John (১৮৮৬)। Nine-Point Circle Theorem, in A Sequel to the First Six Books of Euclid (4th সংস্করণ)। London: Longmans, Green, & Co। পৃষ্ঠা 58।

[PL-5] ক ^খ ^গ ^ঘ Posamentier, Alfred S., and Lehmann, Ingmar. The Secrets of Triangles, Prometheus Books, 2012.

[6] Fraivert, David (জুলাই ২০১৯)। "New points that belong to the nine-point circle"। The Mathematical Gazette। 103 (557): 222–232। ডিওআই:10.1017/mag.2019.53।

[7] Fraivert, David (২০১৮)। "New applications of method of complex numbers in the geometry of cyclic quadrilaterals" (পিডিএফ)। International Journal of Geometry। 7 (1): 5–16।

[8] Altshiller-Court (1925, p. 98)

[9] Altshiller-Court (1925, p. 241)

[১]

[২]

[৩]

[৪]

[৫]

[৬]

[৭]

[৮]

[৯]