পরিগণনামূলক রসায়ন

উইকিপিডিয়া, মুক্ত বিশ্বকোষ থেকে
(গণনামূলক রসায়ন থেকে পুনর্নির্দেশিত)

রসায়নের যে শাখায় পরিগণক যন্ত্র তথা কম্পিউটারের সাহায্যে কোনও রাসায়নিক সমস্যার উত্তর খোঁজা হয় তাকে পরিগণনামূলক রসায়ন (ইংরেজি: Computational chemistry) বলে। এই বিজ্ঞান তাত্ত্বিক রসায়নের পদ্ধতিসমূহ দক্ষ কম্পিউটার প্রোগ্রাম-এর মাধ্যমে কার্যকর করে অণু এবং কঠিন পদার্থের গঠন ও ধর্ম গণনা করে। যেহেতু হাইড্রোজেন আয়ন সংক্রান্ত কিছু সাম্প্রতিক গবেষণা বাদে কোয়ান্টাম বলবিজ্ঞান-এ বহু-বস্তু তত্ত্বের কোনো বিশ্লেষণাত্মক সমাধান নেই, তাই পরিগণনামূলক রসায়ন একটি অত্যন্ত গুরুত্বপূর্ণ ধারা। সাধারণত পরিগণনামূলক ফলাফল রাসায়নিক পরীক্ষার মাধ্যমে অধিকৃত ফলাফলের পূরক হিসাবে কাজ করলেও কিছু ক্ষেত্রে এটি অভূতপূর্ব রাসায়নিক বৈশিষ্ট্যের পূর্বাভাস দিয়েছে। নতুন নতুন ওষুধ এবং নতুন পদার্থ তৈরিতে এটি ব্যাপকভাবে প্রয়োগ হয়।

এরকম কিছু ধর্ম হল গঠন (যেমন পদার্থের উপাদানের পরমাণুগুলির অবস্থান), চরম এবং আপেক্ষিক শক্তি, ইলেক্ট্রন তড়িতাধান ঘনত্ব বিন্যাস, দ্বিমেরু ও উচ্চতর বহুমেরু ভ্রামক, আণবিক কম্পনের কম্পনাঙ্ক, বিক্রিয়াপ্রবণতা এবং অন্যান্য বর্ণালিবীক্ষণ সংলগ্ন বৈশিষ্ট্য, এবং অন্য কণার সাথে বিক্ষেপ প্রস্থচ্ছেদ।

এই পদ্ধতিটি স্থিতি ও গতি সংক্রান্ত সব ক্ষেত্রেই প্রযোজ্য। এই সব ক্ষেত্রেই সিস্টেমের আয়তন বৃদ্ধির সাথে সাথে প্রয়োজনীয় কম্পিউটার সময়-এর পাশাপাশি স্মৃতি-স্থান ও ডিস্ক-স্থান-ও দ্রুত বৃদ্ধি পায়। একটি অণু, একাধিক অণু বা কঠিন পদার্থ দিয়ে এই সিস্টেম গঠিত। পরিগণনামূলক রাসায়নিক পদ্ধতি খুব আনুমানিক থেকে শুরু করে অত্যন্ত সূক্ষ্ম ও নির্ভুল হতে পারে, - কেবলমাত্র খুব ছোটো সিস্টেম-এর ক্ষেত্রেই শেষেরটা সম্ভব। এব-ইনিশিও পদ্ধতির ভিত্তি কেবল কোয়ান্টাম বলবিজ্ঞান এবং প্রাথমিক কিছু ভৌত ধ্রুবকের মান। অন্যান্য পদ্ধতিগুলি পরীক্ষালব্ধ (এম্পিরিকাল) বা অংশত-পরীক্ষালব্ধ (সেমি-এম্পিরিকাল) কারণ এগুলিতে কিছু অতিরিক্ত পরীক্ষালব্ধ প্যারামিটার ব্যবহৃত হয়।

এব-ইনিশিও বা পরীক্ষালব্ধ- দুই পদ্ধতিতেই আসন্নায়ন প্রয়োজন। এই আসন্নায়ন প্রাথমিক মূলনীতি সমীকরণগুলির সরলীকৃত সংস্করণ যার সমাধান অপেক্ষাকৃত সহজ, কিংবা সিস্টেমের আয়তন ছোটো করা (যেমন পর্যাবৃত্ত সীমা শর্ত) থেকে শুরু করে মৌলিক সমীকরণগুলির সমাধানের জন্য কিছু গুরুত্বপূর্ণ আসন্নায়ন-ও হতে পারে। যেমন বেশিরভাগ এব-ইনিশিও গণনায় বর্ন-ওপেনহাইমার আসন্নায়ন ব্যবহার হয়। গণনার সময় নিউক্লিয়াস স্থির থাকে এই আসন্নায়ন ব্যবহার করার দরুন এতে শ্রোডিঙার সমীকরণ-এর ব্যাপক সরলীকরণ সম্ভব।খাতায় কলমে মৌলিক সমীকরণগুলির আসন্নায়ন ধীরে ধীরে হ্রাস করলে এব-ইনিশিও পদ্ধতি সঠিক সমাধানের দিকে অগ্রসর হয়। কিন্তু বাস্তবে কিছু ত্রুটি থেকে যায় কারণ সমস্ত আসন্নায়ন বর্জন করা অসম্ভব। গণনার জটিলতা সাধ্যগত সীমার মধ্যে রেখে এই ত্রুটি ক্ষুদ্রতর করাই পরিগণনামূলক রসায়নের প্রধান লক্ষ্য।

কিছু ক্ষেত্রে ইলেক্ট্রনিক গঠনের খুঁটিনাটি বিবরণের থেকে অনেক বেশি গুরুত্বপূর্ণ দশা-স্থানে অণুর দীর্ঘ সময় ব্যাপী আচরণ। প্রোটিনের কনফর্মেশন বা প্রোটিন-লিগান্ড বন্ধনের তাপগতিবিদ্যায় এই ঘটনা ঘটে। আণবিক গতিবিদ্যার দীর্ঘ সিমুলেশন-এর জন্য বিভব শক্তি-তলের ক্লাসিকাল আসন্নায়ন ব্যবহার হয় কারণ এটি পরিগণনামূলক কম জটিল। অন্যদিকে রসায়ন-ইনফরমেটিক্স -এ ভৌতরাসায়নিক ধর্মের উপর ভিত্তি করে যন্ত্র-শিক্ষনের মত অধিকতর পরীক্ষালব্ধ ও পরিগণনামূলক সহজ পদ্ধতি প্রয়োগ করা হয়। রসায়ন-ইনফরমেটিক্স -এর একটি আদর্শ সমস্যার উদাহরণ হল কোনো লক্ষ্যবস্তুর সাথে ঔষধ অণুর বন্ধন প্রবণতা।

ইতিহাস[সম্পাদনা]

কোয়াণ্টাম বলবিজ্ঞানের ইতিহাসে প্রাথমিক আবিষ্কার এবং মৌলিক নীতিগুলির উপর ভিত্তি করে ১৯২৭ সালে রসায়ন-এ প্রথম তাত্ত্বিক পরিগণনা করেছিলেন ওয়াল্টার হীটলার ও ফ্রীত্জ লন্ডন। পরিগণনামূলক কোয়াণ্টাম রসায়নের প্রাথমিক অগ্রগতিতে যেসব বই গুরুত্বপূর্ণ ভূমিকা পালন করেছিল সেগুলি হল- লিনাস পাওলিং ও ই. ব্রাইট উইলসন-এর "Introduction to Quantum Mechanics – with Applications to Chemistry" (১৯৩৫), আইরিং, ওয়াল্টার ও কিমবল-এর "Quantum Chemistry" (১৯৪৪), হীটলার-এর "Elementary Wave Mechanics – with Applications to Quantum Chemistry" (১৯৪৫), এবং পরবর্তীকালে কুলসন-এর "Valence" (১৯৫২)। এগুলোর প্রত্যেকটাই পরবর্তী দশকগুলিতে রসায়নবিদদের জন্য প্রাথমিক উল্যেক্ষ্য হিসেবে কাজ করেছিল।

১৯৪০ সালে দক্ষ কম্পিউটার প্রযুক্তির ক্রমবিকাশের সাথে সাথে জটিল পারমাণবিক সিস্টেমে তরঙ্গ-সমীকরণের বিশদ সমাধান সম্ভবপর হতে থাকে। পঞ্চাশের দশকের গোড়ার দিকে প্রথম আংশিক পরীক্ষালব্ধ পারমাণবিক অর্বিটাল গণনা করা হয়। প্রথম ডিজিটাল কম্পিউটারগুলির প্রধান ব্যবহারকারী ছিলেন তাত্ত্বিক রসায়নবিদরা। যুক্তরাজ্যে এই ঘটনার বিস্তৃত বিবরণ দিয়েছেন স্মিথ ও সাটক্লিফ। ১৯৫৬ সালে স্লেটার-অর্বিটাল ভিত্তি-সেট ব্যবহার করে MIT তে প্রথমবার দ্বিপরমাণুক অণুর এব-ইনিশিও হারট্রি-ফক গণনা করা হয়। ১৯৬০ সালে দ্বিপরমাণুক অণুর লঘিষ্ঠ ভিত্তি-সেটে যথাযথ বিশ্লেষণ ও বৃহত্তর ভিত্তি-সেটে প্রথম গণনা প্রকাশ করেন যথাক্রমে রান্সিল ও নেসবেট। গাউসিয়ান অর্বিটাল ব্যবহার করে বহুপরমাণুক অণুর প্রথম গণনা করা হয় ১৯৫০ সালের শেষের দিকে। গাউসিয়ান অর্বিটাল ব্যবহার করে প্রথম কনফিগারেশন ইন্টারেক্শন গণনা হয় ক্যামব্রিজের EDSAC কম্পিউটারে ১৯৫০ সালে, করেছিলেন বয়েজ ও অন্যান্যরা। ১৯৭১ সালে এব-ইনিশিও গণনার জে গ্রন্থ-পঞ্জি প্রকাশিত হয় তাতে বৃহত্তম অণু ছিল ন্যাপথ্যালিন ও অ্যাজুলিন। অন্যান্য অনেক এব-ইনিশিও গণনার সারাংশ প্রকাশ করেছেন শেফার।

১৯৬৪ সালে বিউটাডাইন ও বেঞ্জিন থেকে শুরু করে ওভালিন পর্যন্ত নানা জটিল ও সহজ অণুর হুকেল-পদ্ধতি গণনা (সংযুক্ত হাইড্রোকার্বন সিস্টেমের π-আণবিক অর্বিটালে ইলেক্ট্রনিক শক্তি নির্ণয়ের জন্য সরলীকৃত পারমাণবিক অর্বিটালের রৈখিক সংযোগ (LCAO) পদ্ধতি) করা হয় বার্কলি ও অক্সফোর্ডের কম্পিউটারে। ১৯৬০ সালে এই পদ্ধতির জায়গায় CNDO-র মত আংশিক পরীক্ষালব্ধ পদ্ধতি ব্যবহার শুরু হয়।

১৯৭০ সামের শুরুর দিকে আণবিক অর্বিটালের এব-ইনিশিও গণনা দ্রুততর করার জন্য ATMOL, গাউসিয়ান, IBMOL, POLYAYTOM ইত্যাদি দক্ষ এব-ইনিশিও কম্পিউটার প্রোগ্রাম ব্যবহার শুরু হয়। এই চারটির মধ্যে কেবল গাউসিয়ানের উন্নত সংস্করণ এখনো ব্যবহৃত হয়, যদিও এখন অন্য অনেক প্রোগ্রাম ব্যবহারের চল হয়েছে। এই একই সময়ে MM2 বলক্ষেত্রের মত আণবিক বলবিজ্ঞান পদ্ধতির উন্নতি ঘটে নরম্যান এলিংগারের হাত ধরে।

'পরিগণনামূলক রসায়ন' শব্দবন্ধের প্রথম প্রয়োগ পাওয়া যায় সিডনি ফার্নবাক ও আব্রাহাম হাস্কেল টাউব এর ১৯৭০ সালে প্রকাশিত বই "Computers and Their Role in the Physical Sciences"-এ। তারা লিখেছেন, "...তাই মনে হচ্ছে 'পরিগণনামূলক রসায়ন' ধীরে ধীরে বাস্তবে পরিণত হচ্ছে।" ১৯৭০-এর দশকে পরিগণনামূলক রসায়ন নামের এই নতুন বিদ্যায় বিবিধ পদ্ধতি প্রয়োগ হতে থাকে। "Journal of Computational Chemistry" (অর্থাৎ "পরিগণনামূলক রসায়ন গবেষণা সাময়িকী") প্রথম প্রকাশ হয় ১৯৮০ সালে।

পরিগণনামূলক রসায়নবিদরা বেশ কিছু নোবেল পুরস্কার লাভ করেছেন যার মধ্যে সবচেয়ে উল্লেখযোগ্য হল ১৯৯৮ ও ২০১৩ সালের নোবেল পুরস্কারগুলি। "ডেন্সিটি-ফাংশনাল তত্ত্বের উদ্ভাবনের জন্য" ওয়াল্টার কোন, এবং "কোয়ান্টাম রসায়নের নতুন পরিগণনামূলক পদ্ধতি উদ্ভাবনের জন্য" জন পপ্লে ১৯৯৮ সালে রসায়নে নোবেল পুরস্কার পান। ২০১৩ সালে "জটিল রাসায়নিক সিস্টেমের মাল্টিস্কেল মডেলের জন্য" রসায়নে নোবেল পান মার্টিন কারপ্লাস, মাইকেল লেভিট ও এরিয়া ওয়ারশেল।

ব্যবহার[সম্পাদনা]

'তাত্ত্বিক রসায়ন' শব্দবন্ধ ব্যবহার করা যায় রসায়নের গাণিতিক বিশ্লেষণধর্মী ব্যাখ্যার জন্য, অন্যদিকে পরিগণনামূলক পদ্ধতি যখন কম্পিউটারে স্বয়ংক্রিয় প্রয়োগের উপযুক্ত হয় তখন তাকে 'পরিগণনামূলক রসায়ন' বলে। তাত্ত্বিক রসায়নে রসায়নবিদরা, ভৌতবিজ্ঞানীরা এবং গণিতবিদেরা পারমাণবিক ও আণবিক ধর্ম ও রাসায়নিক বিক্রিয়ার বিক্রিয়াপথ নির্ণয়ের জন্য অ্যালগরিদম ও কম্পিউটার প্রোগ্রাম রচনা করেন। অন্যদিকে পরিগণনামূলক রসায়নবিদরা সেই কম্পিউটার প্রোগ্রাম ও পদ্ধতিসমূহ প্রয়োগ করেন নির্দিষ্ট রাসায়নিক সিস্টেমে।

পরিগণনামূলক রসায়নের দুই রকম প্রয়োগ হয়: shI

  • পরীক্ষাগারে সংশ্লেষণের জন্য প্রাথমিক যৌগ নির্ণয় করা বা পরীক্ষালব্ধ তথ্য অনুধাবন করা, যেমন বর্ণালীর শীর্ষের (পিক) স্থান ও উৎস অনুসন্ধান করা।
  • পরীক্ষার মাধ্যমে নিরীক্ষিত হয়নি এমন অজানা অণু বা বিক্রিয়াপথের অনুসন্ধান করা।

এভাবে পরিগণনামূলক রসায়ন পরীক্ষামূলক রসায়নবিদের সাহায্যও করতে পারে, বা পরীক্ষামূলক রসায়নবিদকে নতুন রাসায়নিক বস্তু সন্ধানের দিকে চালিত-ও করতে পারে।

পরিগণনামূলক রসায়নের বেশ কিছু আলাদা আলাদা ক্ষেত্র আছে, যেমনঃ

  • নিউক্লিয়াস এর স্থান পরিবর্তন করে করে শক্তি-তল নির্ণয়ের মাধ্যমে আন্তর-পারমাণবিক বল সিমুলেট করে বা যথার্থ কোয়াণ্টাম রসায়ন পদ্ধতির মাধ্যমে অণুর গঠন নির্ধারন করা।
  • কোনো রাসায়নিক বস্তুর ব্যাপারে তথ্য সংগৃহীত রাখা ও সন্ধান করা (দেখুন রাযায়নিক তথ্যভাণ্ডার)।
  • আণবিক গঠন ও রাসায়নিক ধর্মের মধ্যে সংগতি স্থাপন করা (quantitative structure–activity relationship (QSAR))।
  • রাসায়নিক যৌগের দ্রুত ও দক্ষ সংশ্লেষণের জন্য গণনা করা।
  • পরিগণনামূলকভাবে এমন অণু তৈরি করা যা অন্য কোনো অণুর সাথে পূর্বনির্ধারিত উপায়ে বিক্রিয়া করে (যেমন ঔষধ নকশাকরণ ও অনুঘটন)।

সঠিকতা[সম্পাদনা]

নিখুঁত ও অভ্রান্ত শব্দগুলি এখানে প্রয়োগ হয় না কারণ রসায়নে খুব কম বিষয়্ই ত্রুটি ছাড়া গণনা করা যায়। কিন্তু রসায়নের সব বিষয়েরই গুণগত ও আসন্ন মানগত পরিগণনামূলক বর্ণনা দেওয়া সম্ভব।

যেহেতু নিউক্লিয়াস ও ইলেক্ট্রন নিয়ে অণু গঠিত, তাই কোয়াণ্টাম বলবিজ্ঞানের পদ্ধতিগুলি এখানে প্রযোজ্য। পরিগণনামূলক রসায়নবিদরা অনেকসময় অ-আপেক্ষিক শ্রোডিঙার সমীকরণের সাথে আপেক্ষিকতা সংক্রান্ত সংশোধন যগ করে সমাধান করেন, যদিও সম্পূর্ণরূপ আপেক্ষিক ডিরাক সমীকরণ সমাধানের দিকে কিছুটা অগ্রগতি হয়েছে। খাতায় কলমে সিস্টেম অনুযায়ী শ্রোডিঙার সমীকরণ সময়-নির্ভর ও সময়-অনির্ভর দুইরকম ক্ষেত্রেই সমাধান করা যায়, কিন্তু বাস্তবে খুব ছোটো সিস্টেম ছাড়া সেটা সম্ভব নয়। এরকম ভাবে অভ্রান্ততা ও পরিগণনামূলক জটিলতার মধ্যে ভারসাম্য আনার জন্য প্রচুর সংখ্যক আসন্ন পদ্ধতি তৈরি হয়েছে।

পরিগণনামূলক জটিলতা বাড়ালে গণনার যথার্থতা সবসময়ই বৃদ্ধি পায়। সম্পূর্ণ-আপেক্ষিক গণনার জটিলতার কারণে বহু-ইলেক্ট্রন এব-ইনিশিও মডেলে বেশ কিছু ত্রুটি থাকতে পারে। এই অক্ষমতার কারণে অবস্থান্তর ধাতু ও তাদের অনুঘটক ক্রিয়ার মত উচ্চ পারমাণবিক ভর-সম্পন্ন পরমাণুর সাথে অণুর ক্রিয়ার বিশ্লেষণ কঠিন হয়ে ওঠে। বর্তমানে পরিগণনামূলক রসায়নে যেসব অ্যালগরিদম আছে সেগুলি ৪০ ইলেক্ট্রন অব্দি ধারণকারী অণুর ধর্ম জটিলতা ছাড়া সূক্ষ্মভাবে গণনা করতে পারে।শক্তির মানে ত্রুটির পরিমাণ হতে পারে সামান্য কিছু কিলোজুল/মোল এর থেকেও কম। আণবিক গঠনের ক্ষেত্রে বন্ধন-দূরত্ব কয়েক পিকোমিটার ও বন্ধন-কোণ ০.৫ ডিগ্রির মধ্যে নির্নয় করা যায়। এর থেকে বেশি ইলেক্ট্রন আছে এরকম বৃহত্তর অণুর গণনার জন্য ডেন্সিটি-ফাংশনাল তত্ত্বের মত আসন্ন পদ্ধতি ব্যবহার করা হয়।

জৈবরাসায়নিক বিক্রিয়ার মত জটিল বিক্রিয়ায় এসব আসন্ন পদ্ধতি প্রয়োগের উপযুক্ত কিনা এবিষয়ে বিতর্ক আছে। বৃহত অণুর বিশ্লেষণে অংশত-পরীক্ষালব্ধ আসন্ন পদ্ধতি ব্যবহার করা যায়। অত্যন্ত বড় অণুর ক্ষেত্রে আণবিক বলবিজ্ঞান (Molecular Mechanics (MM)) নামক এক চিরায়ত বলবিজ্ঞান পদ্ধতিরও ব্যবহার আছে। QM-MM পদ্ধতিতে বৃহত সিস্টেমের ক্ষুদ্র অংশগুলিকে কোয়াণ্টাম বলবিজ্ঞানের মাধ্যমে ও বাকিটাকে আসন্নভাবে গণনা করা হয়।

পদ্ধতিসমূহ[সম্পাদনা]

একটি আণবিক সূত্রের সাহায্যে অনেক আণবিক সমাবয়বকে বোঝানো যায়। প্রত্যেক সমাবয়বই হল নিউক্লীয় কো-অর্ডিনেটেরফাংশন সম্পূর্ণ শক্তি (ইলেক্ট্রনীয় শক্তি ও নিউক্লীয় বিকর্ষণ শক্তির যোগফল) দ্বারা রচিত বিভবশক্তি-তলের স্থানীয় মিনিমা। যদি কোনো নির্দিষ্ট আণবিক গঠনের জন্য সমস্ত নিউক্লীয় সরণের সাপেক্ষে শক্তির অন্তরজ শূন্য হয় তবে তাকে স্থানীয় বিন্দু বলে। যে স্থানীয় বিন্দুতে যেকোনো সরণের ফলে শক্তি বৃদ্ধি পায় সেই স্থানীয় বিন্দু হল স্থানীয় মিনিমা। সর্বনিম্ন স্থানীয় মিনিমাকে সার্বজনীন মিনিমা বলে এবং এটি অণুর সবচেয়ে সুস্থিত সমাবয়ব। যদি কোনো একটি নির্দিষ্ট কো-অর্ডিনেটে সরণের ফলে উভয় দিকে শক্তি হ্রাস পায়, তাহলে এটি দশান্তর গঠন এবং সেই কো-অর্ডিনেটটি হল বিক্রিয়া-কোঅর্ডিনেট। স্থায়ী বিন্দু সন্ধানের এই প্রক্রিয়াকে জ্যামিতি অপ্টিমাইজেশন বলে।

সকল পারমাণবিক কো-অর্ডিনেটের সাপেক্ষে শক্তির প্রথম অন্তরজ হিসেবের জন্য দক্ষ পদ্ধতি আবিষ্কারের পরে জ্যামিতি-অপ্টিমাইজেশনের মাধ্যমে আণবিক গঠন নির্ণয়ের চল শুরু হয়। পর্যাবৃত্ত গতি হিসেবে নিলে দ্বিতীয় অন্তরজ থেকে আণবিক কম্পনের কম্পনাঙ্ক নির্ধারণ করা যায়।দ্বিতীয় অন্তরজ নিয়ে যে হেসিয়ান ম্যাট্রিক্স তৈরি হয় তার আইগেনমানের সাথে এই কম্পনাঙ্ক সম্পর্কিত। সব আইগেনমানের মান ধনাত্মক হলে সব কম্পনাঙ্ক বাস্তব সংখ্যা হয় এবং স্থানীয় বিন্দুটি স্থানীয় মিনিমা হয়। যদি একটি আইগেনমানের মান ঋণাত্মক হয় (কম্পনাঙ্কের কাল্পনিক মান), তবে স্থায়ী বিন্দুটি একটি দশান্তর গঠন। একের বেশি আইগেনমানের মান ঋণাত্মক হলে স্থায়ী বিন্দুর প্রকৃতি আরো জটিল হয় এবং এ নিয়ে বেশি চর্চা নেই। এরকম কোনো বিন্দু পাওয়া গেলে স্থানীয় মিনিমা বা দশান্তর গঠনের সন্ধান এর থেকে দূরে গিয়ে করতে হবে।

আপেক্ষিকতা উপেক্ষা করে ও শ্রোডিঙার সমীকরণ সরলীকরণের জন্য বর্ন-ওপেনহাইমার আসন্নায়নের মাধ্যমে ইলেক্ট্রনীয় ও নিউক্লীয় চলণ বিচ্ছিন্ন করার পরে যে সময়-অনির্ভর শ্রোডিঙার সমীকরণ থাকে তার আসন্ন সমাধান থেকে মোট শক্তি হিসাব করা হয়। এই প্রক্রিয়ায় মোট শক্তিকে স্থায়ী নিউক্লীয় কো-অর্ডিনেটে ইলেক্ট্রনীয় শক্তি, এবং নিউক্লীয় বিকর্ষণ শক্তি- এই দুইয়ের যোগফল হিসাবে লেখা যায়। এক উল্লেখযোগ্য ব্যতিক্রম হল প্রত্যক্ষ কোয়াণ্টাম রসায়ন, যাতে নিউক্লীয়াস ও ইলেক্ট্রনকে অভিন্নভাবে দেখা হয়। ডেন্সিটি-ফাংশনাল পদ্ধতি ও অংশত-পরীক্ষালব্ধ পদ্ধতি হল এক-ই মূল ভাবনার ভিন্ন ভিন্ন রূপ। খুব বড় সিস্টেমের ক্ষেত্রে আণবিক বলবিজ্ঞান দ্বারা মোট শক্তি নির্ণয় করা যায়।আণবিক গঠন নির্ধারণের জন্য মোট শক্তি হিসাব করার কিছু পদ্ধতি হলঃ

শূন্য-থেকে-শুরু (অ্যাব-ইনিশিও) পদ্ধতি[সম্পাদনা]

পরিগণনামূলক রসায়নে যেসব প্রোগ্রাম ব্যবহার হয় সেগুলো সবই আণবিক হ্যামিল্টোনিয়ান থেকে যে আণবিক শ্রোডিঙার সমীকরণ আসে তার সমাধানের জন্য নানা কোয়ান্টাম-রাসায়নিক পদ্ধতি। যেসব পদ্ধতিতে কোনও পরীক্ষালব্ধ বা অংশত-পরীক্ষালব্ধ প্যারামিটার নেই এবং যেগুলি কোনো পরীক্ষামূলক তথ্য ছাড়াই শুধুমাত্র তাত্ত্বিক সূত্রগুলি থেকে উতপন্ন হয়েছে সেগুলিকে বলা হয় শূন্য-থেকে-শুরু পদ্ধতি (অ্যাব-ইনিশিও)। যদিও এর থেকে এটা বোঝায় না যে এই সমাধানগুলি অভ্রান্ত, কারণ সবকটিই আসন্ন কোয়াণ্টাম-বলবৈজ্ঞানিক গণনা। এর থেকে শুধু এটাই বোঝায় যে যে আসন্নায়নটি ব্যবহার হয়েছে সেটি কোয়াণ্টাম তত্ত্বের প্রথম সূত্রগুলির পরিপ্রেক্ষিতে যথাযথরূপে সংজ্ঞায়িত এবং সর্বোচ্চ ত্রুটির পরিমাণ গুণগতভাবে জানা। যদি পরিগণনামূলক পুনরাবৃত্তি ব্যবহার হয় তবে যন্ত্রের পূর্ণ ক্ষমতা (কম্পিউটারের সসীম "শব্দ-দৈর্ঘ্য" ও পরিগণনামূলক বা ভৌত আসন্নায়ন মাথায় রেখে) ব্যবহার অব্দি পুনরাবৃত্তি করাই গণনার লক্ষ্য।

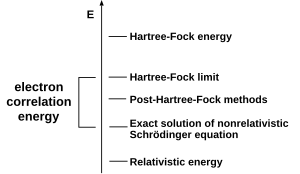
বিভিন্ন শূন্য-থেকে-শুরু ইলেক্ট্রনিক গঠন গণনার আপেক্ষিক শক্তির চিত্র। দূরত্ব স্কেলে নয়।

সরলতম শূন্য-থেকে-শুরু ইলেক্ট্রনিক গঠন গণনা হল হারট্রি-ফক (HF) পদ্ধতি, যা আণবিক কক্ষক তত্ত্বের সংযোজিত সংস্করণ এবং যাতে যথার্থ আন্তর-ইলেক্ট্রনীয় বিকর্ষণের বদলে এর গড় মান নিয়ে গণনা করা হয়। ভিত্তি-সেটের আয়তন বৃদ্ধি করলে শক্তি ও তরঙ্গ-ফাংশন হারট্রি-ফক সীমা নামক সীমার দিকে অগ্রসর হয়। হারট্রি-ফক-পরবর্তী নামের গণনায় হারট্রি-ফক গণনার ফলাফলকে ভিত্তি করে আন্তর-ইলেক্ট্রনীয় বিকর্ষণের জন্য সংশোধন করা একে, যাকে ইলেকট্রনীয় সংশ্লেষ (ইলেকট্রনিক কোরিলেশন) বলে। এই পদ্ধতিকে নিখুঁত করতে থাকলে এই সমাধান আপেক্ষিকতাহীন শ্রোডিঙার সমীকরণের অভ্রান্ত সমাধানের দিকে অগ্রসর হয়। পরীক্ষামূলক ফলাফলের সাথে সম্মতি আনতে হলে আপেক্ষিক ও স্পিন-অর্বিট অংশগুলিকে হিসাবে আনতে হবে, যা ভারী পরামাণুর ক্ষেত্রে গুরুত্বপূর্ণ। এই সমস্ত পরিগণনাতেই পদ্ধতি নির্বাচনের সাথে সাথে ভিত্তি-সেটও বাছাই করতে হয়। এটি হল কিছু ফাংশনের সেট যা অণুর বিভিন্ন পরমাণুর উপর কেন্দ্রীভূত। পারমাণবিক কক্ষকের রৈখিক সংযোগ (LCAO) জাতীয় আণবিক কক্ষক গণনায় আণবিক কক্ষকগুলিকে এই ভিত্তি সেটে সম্প্রসারণ করা হয়। তাই যেকোনও শূন্য-থেকে-শুরু পদ্ধতিতে নির্দিষ্ট পদ্ধতিটি এবং ভিত্তি সেট নির্দেশ করার প্রয়োজন পড়ে।

হারট্রি-ফক তরঙ্গ-অপেক্ষক হল শুধু একটি ইলেক্ট্রনীয় বণ্টনের নির্ণায়ক। বন্ধন ভাঙার মত কিছু প্রক্রিয়ায় এটি অসম্পূর্ণ, এবং বিভিন্ন ইলেকট্রনীয় বণ্টন ব্যবহার করা দরকার। এখানে নির্ণায়কের গুণাঙ্ক এবং ভিত্তি ফাংশনের গুণাঙ্ক একসাথে অপ্টিমাইজ করা হয়।

আণবিক গঠনের ফাংশন হিসেবে মোট আণবিক শক্তি নির্ধারণ করা যায়, যা আসলে বিভবশক্তি-তল। বিক্রিয়া গতিবিজ্ঞানে এই তল ব্যবহার হয়। বিভিন্ন সমাবয়ব ও তাদের মধ্যে দশান্তর গঠন নির্ণয় করা যায় এই তলের স্থায়ী বিন্দুগুলি থেকে। যদিও এর জন্য সম্পূর্ণ বিভবতল গঠন করতে লাগে না।

একটি গুরুত্বপূর্ণ লক্ষ্য হল পরিগণনামূলক তাপগতিবিজ্ঞান, যা থেকে গঠন এনথালপির মত তাপরাসায়নিক রাশি রাসায়নিক মাপকাঠিতে অভ্রান্তভাবে হিসেব করা যায়। রাসায়নিকভাবে অভ্রান্ত বলতে বোঝায় যাতে ত্রুটির ফলে বাস্তব রাসায়নিক গণনায় গুণগত ভুল না হয়, এবং এর মান সাধারণত ১ কিলোক্যালরি/মোল বা ৪ কিলোজুল/মোল। ত্রুটিকে এই সীমায় বাস্তবে নিয়ে যেতে হলে অবশ্যই পোস্ট হারট্রী-ফক গণনা করে তার ফলাফল হিসাবে আনতে হবে। এই পদ্ধতিগুলিকে বলে কোয়াণ্টাম-রসায়ন যৌগিক পদ্ধতি।

ডেন্সিটি-ফাংশনাল পদ্ধতি[সম্পাদনা]

ডেন্সিটি-ফাংশনাল তত্ত্ব (DFT) পদ্ধতিগুলিকে অনেকসময় আণবিক গঠন নির্ধারণের এব-ইনিশিও পদ্ধতি বলে,যদিও প্রচুর প্রচলিত ফাংশনালে পরীক্ষালব্ধ তথ্য বা জটিলতর গণনা থেকে নেওয়া প্যারামিটার ব্যবহৃত হয়। DFTতে মোট শক্তিকে তরঙ্গ-ফাংশনে প্রকাশ না করে মোট এক-ইলেক্ট্রন ঘনত্বতে প্রকাশ করা হয়। এধরনের গণনায় ব্যবহার হয় কোনো আসন্ন হ্যামিল্টনিয়ান এবং মোট ইলেক্ট্রন ঘনত্ব নির্ণয়ের আসন্ন রাশিমালা। DFT পদ্ধতিগুলি স্বল্প পরিগণনামূলক জটিলতায় ত্রুটি খুব কমিয়ে আনতে পারে। কিছু পদ্ধতিতে ঘনত্ব ফাংশনাল ও বিনিময় ফাংশনালের সাথে হারট্রী-ফক বিনিময় রাশিমালা ব্যবহার হয় এবং এগুলিকে বলা হয় মিশ্র ফাংশনাল পদ্ধতি।

পরীক্ষালব্ধ ও অংশত-পরীক্ষালব্ধ পদ্ধতি[সম্পাদনা]

অংশত-পরীক্ষালব্ধ কোয়াণ্টাম রাসায়নিক পদ্ধতিগুলি হারট্রী-ফক পদ্ধতি থেকে শুরু করলেও প্রচুর আসন্নায়ন করে এবং পরীক্ষামূলক তথ্য থেকে কিছু প্যারামিটার ব্যবহার করে। যেখানে আসন্নায়ন ছাড়া পূর্ণ হারট্রী-ফক পদ্ধতি অত্যন্ত জটিল এরকম বড় অণুর পরিগণনামূলক রসায়নে এগুলি খুবই গুরুত্বপূর্ণ। পরীক্ষালব্ধ প্যারামিটার আনার ফলে কোরিলেশনের প্রভাব এখানে কিছুটা আনা সম্ভব।

অংশত-পরীক্ষালব্ধ পদ্ধতির সাথে সম্পর্কিত পরীক্ষালব্ধ পদ্ধতি, যাতে হ্যামিল্টনিয়ানের দুই-ইলেক্ট্রন অংশ স্পষ্টভাবে নেওয়া হয় না। π-ইলেক্ট্রন সিস্টেমের জন্য এটি হচ্ছে এরিক হুকেলের প্রস্তাবিত হুকেল পদ্ধতি, এবং সকল যোজ্য ইলেক্ট্রনের সিস্টেমে এটি রোয়াল্ড হফম্যানের প্রসারিত হুকেল পদ্ধতি।

আণবিক বলবিজ্ঞান[সম্পাদনা]

কিছু ক্ষেত্রে কোয়াণ্টাম রাসায়নিক গণনা সম্পূর্ণরূপে পরিহার করেও বড় আণবিক সিস্টেম মডেল করা যায়। যেমন আণবিক বলবিজ্ঞান সিমুলেশনে কোনো যৌগের শক্তি পরিমাণের জন্য চিরায়ত রাশিমালা ব্যবহার হয়, যেমন আবর্ত দোলক। সমীকরণে যেসব ধ্রুবক আসে সেগুলির মান পরীক্ষার মাধ্যমে বা এব-ইনিশিও গণনার মাধ্যমে আগে থেকে জেনে রাখতে হয়।

আণবিক বলবিজ্ঞান গণনার সাফল্যের জন্য অপরিহার্য হল যৌগের প্যারামিটারগুলির তালিকা। প্যারামিটার ও ফাংশনগুলির এই তথ্যভাণ্ডারকে ফোর্স-ফিল্ড বলে। যে ফোর্স-ফিল্ড একটি নির্দিষ্ট শ্রেনীর অণু থেকে তৈরি হয়েছে (যেমন প্রোটিন) সেটি শুধু সেই শ্রেনীর অন্য অণুর ক্ষেত্রেই কাজে আসে।

এই পদ্ধতিগুলি প্রোটিন বা অন্য বড় জৈব অণুর ক্ষেত্রে প্রয়োগ করা যায়, এবং এর মাধ্যমে সম্ভাব্য ঔষধ অণুর চলন ও বিক্রিয়া(ডকিং)-র আঁচ পাওয়া যায়।

কঠিন পদার্থের জন্য পদ্ধতিসমূহ[সম্পাদনা]

পরিগণনামূলক রসায়নের পদ্ধতিগুলি কঠিন অবস্থা পদার্থবিজ্ঞানে প্রয়োগ করা যায়। কোনো কেলাসের ইলেক্ট্রনিক গঠনের বিবরণে সাধারণত ব্যবহার হয় ব্যান্ড গঠন, যাতে ব্রিলোয়াঁ জোনের প্রতিটি বিন্দুতে ইলেক্ট্রনিক অর্বিটালের শক্তি বর্ণিত থাকে। এব-ইনিশিও ও অংশত-পরীক্ষালব্ধ গণনায় অর্বিটালের শক্তি হিসেব করা যায়; তাই এগুলিকে ব্যান্ড গঠন গণনায় ব্যবহার করা যায়। যেহেতু একটি অণুর শক্তি গণনা করা এক সুদীর্ঘ প্রক্রিয়া, তাই ব্রিলোয়াঁ জোনের সব বিন্দুতে এই গণনা করতে আরো বেশি সময় লাগে।

রাসায়নিক গতিবিদ্যা[সম্পাদনা]

বর্ন-ওপেনহাইমার আসন্নায়নের মাধ্যমে ইলেক্ট্রনীয় ও নিউক্লীয় চলরাশিগুলি পৃথক হয়ে গেলে, সময়-নির্ভর গণনায়, নিউক্লীয় ডিগ্রী অফ ফ্রীডমের তরঙ্গ-প্যাকেটকে পূর্ণ আণবিক হ্যামিল্টোনিয়ান থেকে উদ্ভূত সময়নির্ভর শ্রোডিঙার সমীকরণের সময়-বিবর্তন অপারেটর দিয়ে বিস্তার করা হয়। অন্যদিকে শক্তিনির্ভর গণনায়, সময়-অনির্ভর শ্রোডিঙার সমীকরণকে বিক্ষেপ-তত্ত্ব দিয়ে সমাধান করা হয়। আন্তর-পারমাণবিক বিভব পাওয়া যায় বিভবশক্তি-তল থেকে। সাধারণভাবে বিভবশক্তি-তলগুলি ভাইব্রোনিক-কাপলিং দিয়ে সংযুক্ত থাকে।

আণবিক গঠনের আনুষঙ্গিক তরঙ্গ-প্যাকেটের বিস্তার ঘটানোর জন্য সবথেকে জনপ্রিয় পদ্ধতিগুলি হলঃ

  • স্প্লিট অপারেটর পদ্ধতি
  • (বাস্তব) চেবিশেভ বহুপদ
  • মাল্টি-কনফিগারেশন সময়নির্ভর হারট্রী পদ্ধতি (multi-configuration time-dependent Hartree method (MCTDH))
  • সহ-চিরায়ত (সেমিক্লাসিকাল) পদ্ধতি

আণবিক গতিবিদ্যা[সম্পাদনা]

আণবিক গতিবিদ্যায় (MD) ব্যবহার হয় হয় কোয়াণ্টাম বলবিজ্ঞান, নয়তো নিউটনের গতিসূত্র, অথবা কম্পন বা ব্রাউনিয়ান চলন ও বিক্রিয়ার মত সময়নির্ভর সিস্টেমের জন্য কোনো মিশ্র মডেল। MDর সাথে ডেন্সিটি-ফাংশনাল তত্ত্বর মিলন ঘটালে পাওয়া যায় শঙ্কর মডেল।

আণবিক তরঙ্গ-অপেক্ষকের অর্থ[সম্পাদনা]

রিচার্ড বাডের-এর অণুর মধ্যে পরমাণু (QTAIM) মডেল তৈরি হয়েছিল অণুর তরঙ্গ-অপেক্ষকের মত কোয়াণ্টাম ধারণার সাথে, অণুর মধ্যে পরমাণু,কার্যকরী মূলক,রাসায়নিক বন্ধন, লুইস জোড় তত্ত্ব, ভ্যালেন্স বন্ড মডেল ইত্যাদি রাসায়নিকভাবে কার্যকর ধারণার মেলবন্ধন ঘটানোর জন্য। বাডের দেখিয়েছিলেন যে এইসব পরীক্ষামূলকভাবে কার্যকর ধারণাগুলির সাথে যোগাযোগ আছে পর্যবেক্ষণযোগ্য তড়িত্ ঘনত্ব বিন্যাসের টপোগণিতের সাথে, যা পরীক্ষামূলকভাবে নির্ণয় করা যায় বা কোয়াণ্টাম তরঙ্গ-অপেক্ষক থেকে গণনা করা যায়। AIMAll সফটওয়্যার প্যাকেজে আণবিক তরঙ্গ-অপেক্ষকের QTAIM বিশ্লেষণ করা হয়েছে।

সফটওয়্যার প্যাকেজ[সম্পাদনা]

প্রচুর স্বনির্ভর পরিগণনামূলক রসায়ন সফটওয়্যার প্যাকেজ পাওয়া যায়। তাদের কিছু কিছুতে অনেক রকম পদ্ধতি প্রয়োগ করা আছে, আবার কিছু খুবই স্বল্প, এমনকি একটা পদ্ধতিও প্রয়োগ করেছে। এগুলির বেশিরভাগই হলঃ

  • জৈব অণু মডেলিং প্রোগ্রাম, যেমন প্রোটিন ও নিউক্লিক অ্যাসিড।
  • আণবিক বলবিজ্ঞান প্রোগ্রাম
  • কোয়াণ্টাম রসায়ন ও কঠিন অবস্থা ভৌতবিজ্ঞান সফটওয়্যার
  • আণবিক ডিজাইন সফটওয়্যার
  • অংশত-পরীক্ষালব্ধ (সেমি-এম্পিরিকাল) প্রোগ্রাম
  • ভ্যালেন্স বন্ড প্রোগ্রাম

আরও দেখুন[সম্পাদনা]

তথ্যসূত্র[সম্পাদনা]

গ্রন্থপঞ্জী[সম্পাদনা]

পরিগণনামূলক রসায়নের বিশেষজ্ঞ সাময়িকীসমূহ[সম্পাদনা]

বহিঃসংযোগ[সম্পাদনা]


'https://bn.wikipedia.org/w/index.php?title=পরিগণনামূলক_রসায়ন&oldid=6751935' থেকে আনীত