গড় মান উপপাদ্য

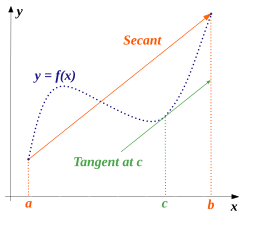
এমন একটি বাস্তব মানবিশিষ্ট - ফাংশন $f$ যা $[a, b]$ বদ্ধ ব্যবধিতে অবিচ্ছিন্ন , $(a, b)$ মুক্ত ব্যবধিতে অন্তরীকরণযোগ্য এবং তাহলে $(a, b)$ মুক্ত ব্যবধিতে একটি সংখ্যা $c$ আছে, যার জন্য $(a,b)$ ব্যবধিতে প্রান্তবিন্দুদ্বয় যোগ করে প্রাপ্ত ছেদক $[a,b]$ ব্যবধিতে $c$ বিন্দুতে অঙ্কিত স্পর্শকের সমান্তরাল হবে ।

f'(c)={\frac {f(b)-f(a)}{b-a}}.

গণিতে, গড় মান উপপাদ্য মোটামুটিভাবে বলে যে, একটি প্রদত্ত রেখার দুটি প্রান্তবিন্দুর মধ্যে , অন্তত একটি বিন্দু আছে যেখানে রেখাটির উপর অঙ্কিত স্পর্শক, রেখাটির প্রান্তবিন্দুদ্বয় দিয়ে গমনকারী ছেদকের সমান্তরাল হবে। এটি বাস্তব বিশ্লেষণের সবচেয়ে গুরুত্বপূর্ণ ফলাফলসমূহের একটি । এই উপপাদ্যটি ব্যবধি বিন্দুতে অন্তরজ সম্পর্কে স্থানীয় অনুমান থেকে শুরু করে একটি বিরতির উপর একটি ফাংশন সম্পর্কে বিবৃতি প্রমাণ করতে ব্যবহৃত হয়।

নিখূঁতভাবে বলতে গেলে উপপাদ্যটি বলে যে, যদি ফাংশন $f$ $[a, b]$ বদ্ধ ব্যবধিতে অবিচ্ছিন্ন , $(a, b)$ মুক্ত ব্যবধিতে অন্তরীকরণযোগ্য, তাহলে $(a, b)$ মুক্ত ব্যবধিতে একটি সংখ্যা $c$ আছে; যার জন্য $(a,b)$ ব্যবধিতে $(a,f(a))$ and $(b,f(b))$ প্রান্তবিন্দুদ্বয় যোগ করে প্রাপ্ত ছেদক $[a,b]$ ব্যবধিতে $c$ বিন্দুতে অঙ্কিত স্পর্শক রেখার সমান্তরাল হবে , এটিকে লেখা যায়:

f'(c)={\frac {f(b)-f(a)}{b-a}}

ইতিহাস

এই উপপাদ্যের একটি বিশেষ ঘটনা প্রথম গোবিন্দস্বমী ও ভাস্কর দ্বিতীয়ের উপর মন্তব্য করতে গিয়ে ভারতের কেরালা স্কুল অব অ্যাস্ট্রোনমি অ্যান্ড ম্যাথমেটিক্সের পরমেশ্বর (১৩৭০–১৪৬০) কর্তৃক বর্ণিত হয়েছিল। ^[১] ১৬৯১ সালে মাইকেল রুলে উপপাদ্যটির একটি সীমাবদ্ধ রূপ প্রমাণ করেন; ফলাফলস্বরুপ যা এখন রুলে'র উপপাদ্য নামে পরিচিত এবং ক্যালকুলাসের কৌশল ছাড়া শুধুমাত্র বহুপদীদের জন্য তিনি উপপাদ্যটি প্রমাণ করেছিলেন। এর আধুনিক রূপে গড় মান উপপাদ্যটি ১৮২৩ সালে ওগুস্তাঁ লুই কোশি দ্বারা বর্ণিত এবং প্রমাণিত হয়।^[২] তখন থেকেই এই উপপাদ্যের বিভিন্ন প্রকরণ প্রমাণিত হয়েছে। ^[৩]^[৪]

(f(b)-f(a))g'(c)=(g(b)-g(a))f'(c).

আরও দেখুন

তথ্যসূত্র

↑ J. J. O'Connor and E. F. Robertson (2000). Paramesvara ওয়েব্যাক মেশিনে আর্কাইভকৃত ২ এপ্রিল ২০১৫ তারিখে, MacTutor History of Mathematics archive.
↑ Ádám Besenyei। "Historical development of the mean value theorem" (পিডিএফ)। ৩০ অক্টোবর ২০২০ তারিখে মূল থেকে আর্কাইভকৃত (পিডিএফ)। সংগ্রহের তারিখ ২৪ মার্চ ২০২১।
↑ Lozada-Cruz, German (২ অক্টোবর ২০২০)। "Some variants of Cauchy's mean value theorem" (ইংরেজি ভাষায়): ১১৫৫–১১৬৩। ডিওআই:10.1080/0020739X.2019.1703150। আইএসএসএন 0020-739X। {{সাময়িকী উদ্ধৃতি}}: উদ্ধৃতি journal এর জন্য |journal= প্রয়োজন (সাহায্য)
↑ Sahoo, Prasanna. (১৯৯৮)। Mean value theorems and functional equations। Riedel, T. (Thomas), 1962-। World Scientific। আইএসবিএন ৯৮১-০২-৩৫৪৪-৫। ওসিএলসি 40951137।

বহিঃসংযোগ

* প্ল্যানেট ম্যাথ: গড়-মান উপপাদ্য ওয়েব্যাক মেশিনে আর্কাইভকৃত ১৮ নভেম্বর ২০০৯ তারিখে

এরিক ডব্লিউ. ওয়াইস্টাইন সম্পাদিত ম্যাথওয়ার্ল্ড থেকে "Mean value theorem"।
এরিক ডব্লিউ. ওয়াইস্টাইন সম্পাদিত ম্যাথওয়ার্ল্ড থেকে "Cauchy's Mean-Value Theorem"।
খান একাডেমিতে "গড় মান উপপাদ্য: অন্তর্নিহিত মূল্যের উপপাদ্য" behind

[1] J. J. O'Connor and E. F. Robertson (2000). Paramesvara ওয়েব্যাক মেশিনে আর্কাইভকৃত ২ এপ্রিল ২০১৫ তারিখে, MacTutor History of Mathematics archive.

[2] Ádám Besenyei। "Historical development of the mean value theorem" (পিডিএফ)। ৩০ অক্টোবর ২০২০ তারিখে মূল থেকে আর্কাইভকৃত (পিডিএফ)। সংগ্রহের তারিখ ২৪ মার্চ ২০২১।

[3] Lozada-Cruz, German (২ অক্টোবর ২০২০)। "Some variants of Cauchy's mean value theorem" (ইংরেজি ভাষায়): ১১৫৫–১১৬৩। ডিওআই:10.1080/0020739X.2019.1703150। আইএসএসএন 0020-739X। {{সাময়িকী উদ্ধৃতি}}: উদ্ধৃতি journal এর জন্য |journal= প্রয়োজন (সাহায্য)

[4] Sahoo, Prasanna. (১৯৯৮)। Mean value theorems and functional equations। Riedel, T. (Thomas), 1962-। World Scientific। আইএসবিএন ৯৮১-০২-৩৫৪৪-৫। ওসিএলসি 40951137।

[১]

[২]

[৩]

[৪]